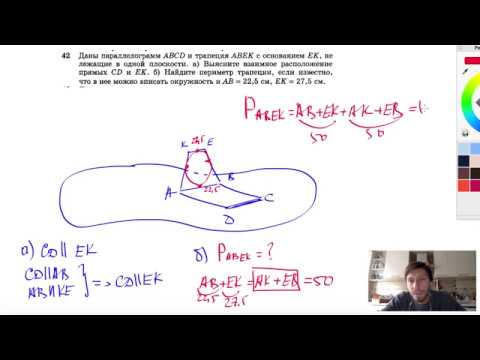
Кто знает ответ? Даны четыре точки. Известно, что прямая, проходящая через любые две из этих точек, не пересекается с прямой, проходящей через другие две точки. Докажите, что данные четыре точки не лежат в одной плоскости.
Допустим, что точки А, В, С, D лежат в одной плоскости. Тогда
прямые АВ и CD, АС и BD параллельны, поэтому точки А, В, С, D
являются вершинами параллелограмма ABCD. Но тогда диагонали
AD и ВС этого параллелограмма должны пересекаться, что проти-
воречит условию задачи. Значит А, В, С и D не лежат в одной плос-
кости. Что и требовалось доказать.
Видео:№4. Точки А, В, С и D не лежат в одной плоскости, а) Могут ли какие-то три изСкачать
Теоретические самостоятельные работы по геометрии
Теоретические самостоятельные работы по геометрии
Подготовила учитель математики
МОУ Дугдинская СОШ
Проверочная работа №1.
Аксиомы стереометрии и следствия из них
1. Верно ли, что если концы отрезка лежат в данной плоскости, то и его середина лежит в данной плоскости?
2. Могут ли две плоскости иметь общую точку, но не иметь общей прямой?
3. Точка А не лежит в плоскости KMN. Назовите прямую пересечения плоскостей AMN и AKM.
4. Даны точки А, В, С и D. Плоскость α проходит через прямую АВ, но не проходит через точку С. Прямые AD и ВС пересекаются в точке В. Сколько данных точек лежит в плоскости α?
5. В пространстве даны прямая и точка. Сколько различных плоскостей можно через них провести?
6. *Верно ли, что если три данные точки лежат в одной плоскости, то они не лежат на одной прямой?
7. *Могут ли три прямые иметь общую точку, но не лежать в одной плоскости?
8. *Три прямые пересекаются в точке А. Через данную точку необходимо провести плоскость, содержащую ровно две из трех данных прямых.
Сколько таких плоскостей можно провести? Рассмотрите все возможные случаи.
одну или бесконечно много
три или не одной
Проверочная работа №2.
Параллельные прямые в пространстве.
Параллельность прямой и плоскости
1. Верно ли, что две параллельные прямые лежат в одной плоскости?
2. Может ли прямая, параллельная плоскости, пересекать какую-либо прямую этой плоскости?
3. Определите взаимное расположение прямой а и плоскости α, если:
a || b и прямая b пересекает плоскость α.
4. Дана плоскость β и прямые а, b, с. Известно, что одна из данных прямых параллельна плоскости β. Назовите эту прямую, если:
а || с , прямые b и с пересекаются, а прямая с лежит в плоскости β.
5. Может ли прямая в пространстве пересекать одну из двух параллельных прямых, но не пересекать другую?
6. Определите взаимное расположение прямой а и плоскости α, если в плоскости α не существует прямой, пересекающей а.
7. Верно ли, что две прямые, параллельные одной плоскости, параллельны?
8. Могут ли прямые AB и CD быть параллельными, если прямые AD и BC пересекаются?
Проверочная работа №3.
Взаимное расположение прямых в пространстве
1. Верно ли, что если две прямые в пространстве не пересекаются, то они параллельны?
2. Может ли угол в пространстве быть тупым?
3. Определите взаимное расположение прямых a и b , если прямая а лежит в плоскости α, а прямая b пересекает плоскость α в точке, не лежащей на прямой а.
4. Прямая l пересекает плоскость треугольника АВС в точке В. Назовите прямую, скрещивающуюся с l и содержащую сторону данного треугольника.
5. Определите, верно ли на плоскости, в пространстве или и на плоскости, и в пространстве данное утверждение:
«Если две различные прямые не пересекаются, то они параллельны.
6. Верно ли, что две прямые, параллельные одной плоскости, могут быть скрещивающимися?
7. Могут ли в пространстве два угла с соответственно параллельными сторонами не быть равными?
8. Определите, какой из случаев взаимного расположения прямых a и b невозможен, если прямая а пересекается с с, а b||с.
Проверочная работа №4.
Тетраэдр и параллелепипед
1. Верно ли, что прямая, лежащая в одной из двух параллельных плоскостей, параллельна второй плоскости?
2. Могут ли рёбра тетраэдра лежать на параллельных прямых?
3. Параллельные плоскости α и β пересекают плоскость γ по прямым a и b соответственно. Определите взаимное расположение прямых a и b .
4. Определите вид сечения параллелепипеда плоскостью, проходящей через середины четырёх боковых рёбер.
5. Дана плоскость α и точка А вне данной плоскости. Определите, какую фигуру в пространстве образуют все прямые, параллельные данной плоскости и проходящие через данную точку. Как расположена эта фигура по отношению к плоскости α?
6. Верно ли, что если в каждой из двух параллельных плоскостей проходит прямая, то эти прямые скрещивающиеся?
7. Может ли в тетраэдре DABC грань DBC содержать прямую, параллельную ребру DA?
8. Плоскость γ пересекает параллельные плоскости α и β по прямым a и b соответственно. Прямая с скрещивается с прямой b . Укажите, какой из случаев взаимного расположения прямых а и с невозможен.
9. Определите, какую фигуру в пространстве образуют середины всех отрезков с концами на двух данных скрещивающихся прямых. Как расположена эта фигура по отношению к данным прямым?
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

22. Даны четыре точки А, В, С, D, не лежащие в одной плоскости. Докажите, что любая плоскость, параллельная прямым АВ и CD, пересекает прямые АС, AD, BD и ВС в вершинах параллелограмма.
Допустим некоторая плоскость α параллельна прямым АВ и CD.
Согласно утверждению: если плоскость β проходит через прямую а, параллельную другой плоскости α, и пересекает эту плоскость по второй прямой b, то прямые а и b параллельны. Из параллельности прямой АВ и плоскости α следует, что плоскости
определенные тремя точками АВС и ABD пересекают плоскость α по прямым а и b, параллельным прямой АВ. Из теоремы 17.2 следует, что прямые а и b параллельны.
Из параллельности прямой CD и плоскости α следует, что плоскости ACD и BCD пересекают плоскость α прямым с и d параллельным прямой CD, а, значит, cd. Каждая из точек пересечения плоскости α с прямыми АС, AD, BD, ВС лежат в плоскости α и является точкой пересечения каких-то двух не параллельных из прямых а, b, c, d. Например, точка пересечения прямой АС с плоскостью α принадлежит плоскостям АВС и ACD, а значит является точкой пересечения прямых b и с, где b и с — прямые пересечения плоскости α с плоскостями АВС и ACD соответственно.
Так как прямые а и b, с и d попарно параллельны, то построенная по условию задачи фигура есть параллелограмм. Что и требовалось доказать.

задача №22
к главе «§ 16. Параллельность прямых и плоскостей».
🎦 Видео
Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Доказать, что точки лежат в одной плоскости - bezbotvyСкачать

Как проверить лежат ли 4 точки в одной плоскости Аналитическая геометрияСкачать

Параллельность прямой и плоскости. 10 класс.Скачать

№11. Даны прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие черезСкачать

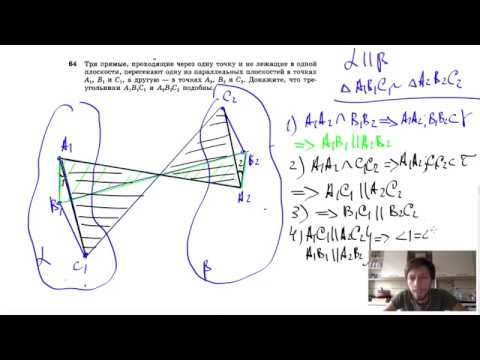
№64. Три прямые, проходящие через одну точку и не лежащие в одной плоскости, пересекают однСкачать
10 класс, 3 урок, Некоторые следствия из аксиомСкачать

10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№3. Верно ли, что: а) любые три точки лежат в одной плоскости;Скачать

Параллельность прямых. 10 класс.Скачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Точка, прямая и отрезок. 1 часть. 7 класс.Скачать

№72. Даны четыре прямые, каждые две из которых пересекаются. Сколько точекСкачать
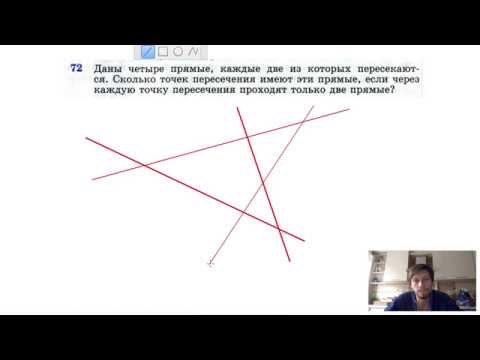
№42. Даны параллелограмм ABCD и трапеция ABEK с основанием ЕК, не лежащие в одной плоскости,Скачать