Даны 2 параллельные прямые и точки р и q на одной из них

Геометрия | 10 — 11 классы

Даны две параллельные прямые и точки P, Q на одной из них.

Через эти точки проведены две параллельные плоскости, которые пересекают вторую прямую в точках Р1 и Q1.

Чему равна длина отрезка P1Q1, если PQ = 6, 3.

Параллельные плоскости отсекают на параллельных прямых равные отрезки, значит P₁Q₁ = PQ = 6, 3.

Но ее можно и доказать.

Параллельные прямые задают плоскость.

Если эта плоскость пересекает параллельные плоскости α и β, то линии пересечения параллельны.

Получаем, что PP₁ ║ QQ₁ и PQ ║ PQ₁, значит PP₁Q₁Q — параллелограмм, значит противолежащие стороны равны.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Даны две параллельные прямые и точки Р и Т на одной из них?

Даны две параллельные прямые и точки Р и Т на одной из них.

Через эти точки проведены параллельные плоскости, которые пересекают вторую прямую в точках Р1 и Т1 соответственно.

Чему равна длина отрезка Р1Т1, если РТ = 6, 3дм?

С решением плииииз!

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

1а Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются?

1а Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

2а Через точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной прямой, и притом только одна.

3а Если одна из двух параллельных прямых пересекает третью прямую, то и другая прямая пересекает эту прямую.

4а Две прямые, пересекающие третью прямую, пересекаются между собой.

5а Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

6а Если две прямые перпендикулярны третьей, то они параллельны друг другу.

7в Если одна из двух параллельных прямых пересекает третью прямую, то другая прямая лежит в одной плоскости с первой и третьей прямыми.

8в Две непараллельные прямые, пересекающие третью прямую, пересекаются между собой.

9в Если две параллельные прямые пересекаются третьей, то все три прямые лежат в одной плоскости.

10с Если параллельные прямые лежат в одной плоскости, то и прямая, имеющая общую точку с одной из них, лежит в этой же плоскости.

11с Три попарно непересекающиеся и непараллельные прямые лежат в трех разных плоскостях.

12с Две непараллельные прямые, пересекающие две данные параллельные прямые, пересекаются между собой.

Помогите пожалуйста, нужны все правильные ответы!

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Даны две параллельные плоскости?

Даны две параллельные плоскости.

Через точки М и N принадлежащие одной из этих плоскостей проведены параллельные прямые пересекающие вторую плоскость в

Чему равна длина отрезка М1 n1 если МN = 8, 8СМ.

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Через конец А отрезка АВ проведена плоскость а?

Через конец А отрезка АВ проведена плоскость а.

Через точку В и точку С, лежащую на отрезке АВ, проведены параллельные прямые, пересекающие плоскость а в точках В1 и С1.

Докажите, что точки А, В1 и С1 лежат на одной прямой.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Даны две параллельные плоскости?

Даны две параллельные плоскости.

Прямая а пересекает эти плоскости в точках А1 и А2, а параллельная ей прямая b в точках В1 и В2 соответственно.

Чему равна длина отрезка В1В2, если А1А2 = 3, 5м?

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Помогите пожалуйста34?

A) Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.

B) В любом треугольнике каждая сторона больше суммы двух других сторон.

C) Если две различные прямые имеют общую точку, то через них можно провести множество плоскостей.

D) Через четыре точки не лежащие на одной прямой можно провести плоскость и притом только одну.

Прямые в пространстве параллельны если они лежат в одной плоскости и имеют две общие точки

b) Через точку пространства можно провести прямую параллельную данной и при том только одну.

C) Если две параллельные прямые пересекают третью, то все они параллельны

d) Если две прямые не пересекаются и не лежат в одной плоскости, то они скрещивающиеся.

Прямая и плоскость называются параллельными, если они имеют две общие точки.

B) Если прямая не лежащая в данной плоскости, параллельна какой — нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

C) Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей не параллельна данной прямой.

D) Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая пересекает эту плоскость.

Если две пересекающиеся прямые одной плоскости параллельны двум прямым другой плоскости , то такие плоскости пересекаются.

B) Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны

c) Отрезки параллельных прямых заключенных между параллельными плоскостями пересекаются.

D) Две плоскости называются параллельными если они имеют общие точки.

38. Если одна из двух параллельных прямых перпендикулярна к третьей, то другая прямая

Перпендикулярна этой прямой

b) Параллельна этой прямой

Скрещивается с этой прямой

d) Не возможно определить.

39. Если две прямые перпендикулярны к плоскости, то они между собой :

Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости

Пересекаются под острым углом

Расстояние между параллельными плоскостями в пространстве измеряют по

b) По проекции наклонной

d) Неважно как измерять.

Видео:№124. Прямая PQ параллельна плоскости α. Через точки Р и Q проведены прямые, перпендикулярныеСкачать

Даны две параллельные плоскости?

Даны две параллельные плоскости.

Прямая а пересекает эти плоскости в точках А1и А2, а параллельная ей прямая b в точках В1 и В 2.

Чему равна длина отрезка В1В2, если А1А2 = 3, 5м ?

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Даны две параллельные плоскости?

Даны две параллельные плоскости.

Прямая а пересекает эти плоскости в точках А1 и А2 а паралельная ей прямая в в точках В1 и в2 соответственно.

Чему равна длина отрезка В1В2 если А1А2 = 3.

Видео:Параллельные прямые (задачи).Скачать

Выберете верное утверждение : 1 )Если две прямые параллельны одной и то же плоскости , то они параллельны, 2) через точку , лежащую на плоскости, можно провести единственную прямую , перпендикулярную ?

Выберете верное утверждение : 1 )Если две прямые параллельны одной и то же плоскости , то они параллельны, 2) через точку , лежащую на плоскости, можно провести единственную прямую , перпендикулярную данной плоскости, 3)если две различные прямые перпендикулярны одной плоскости , то они параллельны , 4)три несовпадающие плоскости всегда пересекаются по одной прямой или точке.

Видео:Пересекающиеся и параллельные прямые, лучи, отрезки. Задачи. Геометрия. Математика 2 класс.Скачать

Даны две параллельные прямые а и б и точка М не лежащая ни на одной из них?

Даны две параллельные прямые а и б и точка М не лежащая ни на одной из них.

Точка М лежит в одной плоскости с прямыми а и б, если через точку М можно провести прямую, пересекающую.

1) хотя бы одну из данных прямых.

2) только одну из данных прямых.

2) две данные прямые.

Вопрос Даны две параллельные прямые и точки P, Q на одной из них?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 10 — 11 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

Первый случай — расположение по разные стороны от прямой. Воспользуемся координатным методом. Координата нужна только одна, х, вторая, y, не важна и мы её просто не будем указывать S1(18), И1( — 8) Координата точки Щ1 найдётся как среднее арифметич..

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Даны две параллельные прямые и точки P, Q на одной из них. Через эти точки проведены две параллельные плоскости, которые пересекают вторую прямую в точках Р1 и Q1. Чему равна длина отрезка P1Q1, если PQ=6,3.Ответ поясните.

Поделись вопросом в социальных сетях!

Если Вы не получили ответ на свой вопрос, то предлагаем воспользоваться поиском, чтобы найти похожие вопросы и ответы по предмету -> Геометрия. А если Вы знаете правильный ответ сами, то будем признательны если Вы ответите, воспользовавшись формой ниже.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Введение (стр. 4 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5

lх3 = у1 + у2 + у3.

C = – матрица перехода от нового проективного репера к старому. Определитель матрицы С отличен от нуля, так как точки A1¢, A2¢, A3¢ неколлинеарные, то есть не лежат на одной прямой, векторы их порождающие ¢, ¢, ¢ линейно независимы.

2. Система векторов ¢, ¢, ¢, ¢ не согласована относительно репера R¢, то есть вектор ¢, порождающий точку E¢, не равен сумме векторов, порождающих точки A1¢, A2¢, A3¢: ¢ ¹ ¢ + ¢ + ¢.

Нам нужно получить согласованную систему векторов относительно R¢. Для этого вместо векторов ¢, ¢, ¢ возьмем векторы = k1¢, = k2¢, = k3¢, согласованные относительно репера R¢ и порождающие точки A1¢, A2¢, A3¢ соответственно. Тогда будем иметь:

¢ = k1¢ + k2¢ + k3¢ (7)

Равенство (7) запишем в координатной форме:

k1 + k2 + k3 = ,

k1 + k2 + k3 = , (8)

k1 + k2 + k3 = .

На (8) смотрим как на систему с неизвестными k1, k2, k3. Система (8) неоднородная, и так как определитель этой системы отличен от нуля, то k1, k2, k3 из этой системы определяются однозначно, причем k1, k2, k3 не равны нулю одновременно. Матрица

C1 = является матрицей перехода от репера R к реперу R¢для второго случая.

Замечание. Используя формулы (6) легко записать формулы преобразования проективных координат на проективной прямой. Они имеют следующий вид:

lх1 = у1 + у2,

lх2 = у1 + у2, (9)

Составить формулы преобразования проективных координат при переходе от репера R = <A1, A2, A3, E> к реперу R¢ = <A1¢, A2¢, A3¢, E¢>, если в репере R: A1¢(1, 0, –1), A2¢(2, 1, 0), А3¢(0, 0, 1); а) E¢(3, 1, 0), б) E¢(1, 1, 2).

а) Пусть , , система векторов, согласованная относительно репера R.

Пусть далее ¢, ¢, ¢ – векторный базис репера R¢.

p(¢) = A1¢, ¢; p(¢) = A2¢, ¢; p(¢) = A3¢, ¢. Найдем сумму векторов:

¢ + ¢ + ¢ = . Видим, что сумма ¢ + ¢ + ¢ есть вектор, порождающий точку Е¢: p(¢ + ¢ + ¢) = Е¢. Значит, в случае а) система векторов <¢, ¢, ¢> согласована относительно репера R¢ и мы воспрользуемся формулами перехода (6).

Подставив в правые части формул (6) координаты точек A1¢, A2¢, A3¢, мы получим искомые формулы преобразования проективных координат:

б) В этом случае сумма векторов ¢ + ¢ + ¢ = не порождает точку Е¢, то есть система векторов <¢, ¢, ¢> не согласована относительно репера R¢. Значит, нужно найти базис, определяющий репер R¢.

Обозначим – вектор, порождающий точку Е¢, p() = Е¢ и найдем векторы

= k1¢, = k2¢, = k3¢, такие, что

k1¢ + k2¢ + k3¢ = ¢ (10)

Подставим в равенство (10) разложения векторов ¢, ¢, ¢, ¢ по векторам базиса <, , >, где <, , > – векторный базис проективного репера R:

¢ = – , ¢ = 2 + , ¢ = , ¢ = + + 2.

Подставляем ¢, ¢, ¢, ¢ в (10), получим:

+ + 2 = k1( – ) + k2(2 + ) + k3.

(k1 + 2k2) + k2 + (k3 – k1) = + + 2.

То есть, = –¢, = ¢, = ¢. Матрица перехода в формулах (5) имеет вид:

.

Значит, искомые формулы преобразования координат будут следущими:

Задачи для самостоятельного решения.

1. Написать формулы преобразования координат при переходе от системы R = <A1, A2, A3, E> к системе R¢ = <A1¢, A2¢, A3¢, E¢>, если:

2. Написать формулы преобразования координат при переходе от системы координат R = <A1, A2, A3, E> к системе R¢ = <A1, A2, A3, E¢>, если E¢ в исходной системе координат имеет координаты
(–1, 2, 3).

3. Написать формулы преобразования координат, если точки A1¢, A2¢, A3¢, E¢, определяющие репер R¢, имеют относительно старой системы координат R = <A1, A2, A3, E> следующие координаты: A1¢(1, 1, 0), A2¢(0, –1, 2), A3¢(1, 1, 1), E¢(2, 3, –5).

4. На плоскости даны 2 системы координат: R = <A1, A2, A3, E> и R¢ = <A1¢, A2¢, A3¢, E¢>, точки A1¢, A2¢, A3¢, E¢ имеют в координатной системе R следующие координаты:

а) Найти координаты точки М в системе R¢, если известны ее координаты в системе R: М(1, 1, 1).

б) Найти уравнение прямой в репере R¢, если известно ее уравнение с репере R: х1 + 2х2 = 0.

в) Найти уравнение прямой в системе R, если известно ее уравнение с системе R¢: у1 + 2у2 = 0.

5. Вершины координатного треугольника и единичная точка проективного репера R¢ имеют на расширенной плоскости следующие аффинные координаты: А1¢(0, 3), А2¢(4, 0), А3¢(4, 3), E¢(3, 2)

а) проективные координаты точки М, если ее аффинные кординаты М(1, 1);

б) аффинные координаты точки Р, если ее проективные координаты Р(4, 3, –6).

в) проективные координаты несобственной точки оси абсцисс;

г) проективные координаты несобственной точки оси ординат;

д) проективные координаты несобственной точки прямой х – 2у + 1 = 0;

е) однородные координаты точки К, если ее проективные координаты K(5, 5, –7).

6. Единичная точка Е проективного репера R = <A1, A2, A3, E> на расширенной плоскости является точкой пересечения медиан координатного треугольника A1A2A3. Найти координаты несобственных точек сторон координатного треугольника и координаты несобственных точек его медиан относительно репера R.

7. В прямоугольных декартовых координатах дано уравнение кривой х2 – 2ху + у2 + 4х + 4у – 8 = 0.

а) уравнение данной кривой в однородных координатах;

б) несобственные точки кривой, доказав при этом, что данная кривая является параболой;

в) направляющий вектор оси параболы;

г) координаты вершины и уравнение оси параболы в неоднородных координатах.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

§5. Принцип двойственности. Теорема Дезарга.

На проективной плоскости и в пространстве справедлив принцип двойственности. Сформулируем принцип двойственности для проективной плоскости.

Если на проективной плоскости справедливо некоторое предложение А, в котором идет речь о точках прямых и их взаимной принадлежности, то будет справедливо предложение А¢, которое получается из утверждения А путем замены слова «точка» на слово «прямая»: «прямая» – «точка»; «лежит на» – «проходит через», «проходит через» – «лежит на».

Предложение А: Через любые две точки проективной плоскости проходит единственная прямая.

Двойственное ему предложение А¢: Любые две прямые пересекаются в одной точке.

Рассмотрим далее теорему Дезарга и проиллюстрируем на ней применение принципа двойственности. Возьмём на проективной плоскости три различные точки A, B, C, не лежащие на одной прямой (рис. 27).

Фигура, состоящая из трёх точек, не лежащих на одной прямой, и трёх прямых, соединяющих попарно эти точки, называется трёхвершинником.

Точки A, B, C называются вершинами, а прямые AB, BC, AC – сторонами трёхвершинника.

Трёхвершинник с вершинами A, B, C обозначается так: ABC.

Пусть даны два трёхвершинника ABC и A¢B¢C¢, такие, что ни одна из вершин или сторон одного трёхвершинника не совпадает с соответствующим элементом другого (рис 28). Тогда имеет место теорема Дезарга:

Теорема. Если три прямые (AA¢), (BB¢), (CC¢), проходят через одну точку, то точки пересечения прямых а Ç a¢, b Ç b¢, c Ç c¢ лежат на одной прямой.

Доказательство теоремы Дезарга мы не приводим. Сформулируем теорему обратную теореме Дезарга:

Даны два трехвершинника и никакие их вершины и стороны не совпадают. Тогда, если точки пересечения соответственных сторон а Ç a¢, b Ç b¢, c Ç c¢ этих трехвершинников лежат на одной прямой, то прямые (AA¢), (BB¢), (CC¢), проходящие через соответственные вершины трёхвершинников, пересекаются в одной точке.

Дополняя евклидову плоскость несобственными точками, мы получим расширенную плоскость, которая является моделью проективной плоскости. Значит, для решения задач евклидовой геометрии можем использовать факты проективной геометрии, в частности, теорему Дезарга.

На чертеже ограниченных размеров заданы две пары прямых: р и q, пересекающиеся в недоступной точке А, и u и v, пересекающиеся в недоступной точке В. Построить доступную часть прямой АВ.

Точку пересечения двух прямых будем называть недоступной, если прямые пересекаются за пределами чертежа.

Задача сводится к построению двух доступных точек прямой (АВ), где А = р Ç q, В = u Ç v. Используя теорему Дезарга, доступную точку С прямой АВ можем построить как точку пересечения соответственных сторон двух трёхвершинников, у которых двумя парами соответственных сторон служат прямые р и q, u и v, а прямые, проходящие через соответственные вершины, пересекаются в некоторой точке S. M = u Ç p и M¢ = v Ç q – соответствующие вершины. Возьмём любую точку S Î (MM¢), не лежащую на данных прямых. Через точку S проведём две прямые m и n, пересекающие данные прямые в доступной части чертежа. N = n Ç u, N¢ = n Ç v; K = m Ç p, K¢ = m Ç q. Рассмотрим два трёхвершинника: MNK и M¢N¢K¢. Прямые ММ¢, NN¢, KK¢ проходят через одну точку S. Значит, по теореме Дезарга, точки пересечения прямых (NM) Ç (N¢M¢) = А, (KM) Ç (K¢M¢) = B, (NK) Ç (N¢K¢) = C лежат на одной прямой. То есть, доступная точка С Î АВ. Для построения ещё одной доступной точки D прямой АВ построим конфигурацию Дезарга так, чтобы прямые р и q составляли одну пару соответственных сторон, другая пара сторон пересекалась в точке С, а третья – в доступной точке D. А прямые, проходящие через соответственные вершины, пересекались в произвольной точке S¢, не принадлежащей прямым р и q. Через точку S¢ проведём произвольные прямые a и b. b Ç р = R, b Ç q = R¢, a Ç р = T, a Ç q = T¢. Построим прямые (RС) и (R¢С¢). Возьмём точку Z Î RC и построим Z¢ = S¢Z Ç R¢C. Рассмотрим два трёхвершинника TRZ и T¢R¢Z¢. Так как (ТТ¢) Ç (RR¢) Ç (ZZ¢) = S¢, то точки А = р Ç q, C, D = (ZT) Ç (Z¢T¢) лежат на одной прямой. Итак, А, В, С, D Î (AB). Точки С и D доступные точки прямой АВ. Строим (СD) – доступную часть прямой АВ. На евклидовой плоскости даны параллелограмм NKLМ, прямая n и точка А, не принадлежащая ни прямой n, ни сторонам параллелограмма. Пользуясь одной линейкой, проведите прямую через данную точку параллельно прямой n. Построим сначала произвольную прямую, параллельную прямой n. Для этого строим два трёхвершинника XYN и X¢Y¢L, где Х = n Ç NK, Y = n Ç NМ. Прямые (ХХ¢), (YY¢), (NL) пересекаются в одной точке. Следовательно, трёхвершинники XYN и X¢Y¢L удовлетворяют теореме Дезарга и прямые XN и X¢L , YN и Y¢L, XY и X¢Y¢ пересекаются на одной прямой. Но стороны трёхвершинников XN и X¢L, YN и Y¢L параллельны. Следовательно, XY || X¢Y¢, т. е. n || X¢Y¢.Обозначим прямую, параллельную прямой n через l. Имеем теперь две параллельные прямые n, l и точку А. Для построения прямой, параллельной данной, найдём точку В. Для этого, построим конфигурацию Дезарга так, что одну пару соответственных сторон составили прямые l и n, другая – пересекались в точке А, а третья – в искомой точке. Возьмем на отрезке RА произвольную точку Р и построим точку Р¢ = S¢Р Ç АR¢. Два трёхвершинника RQР и R¢Q¢Р¢ удовлетворяют теореме Дезарга, прямые RQ и R¢Q¢, RP и R¢P¢, QR и Q¢R¢ пересекаются на одной прямой, т. е. A, B, D¥ = n Ç l принадлежат одной прямой. D¥ Î (AB), следовательно прямая AB || n. На евклидовой плоскости трапеция вписана в четырёхугольник так, что её параллельные стороны параллельны одной из его диагоналей. Докажите, что непараллельные стороны трапеции пересекаются на другой диагонали.

Трапеция EFQM вписана в четырёхугольник ABCD так, что FQ || EМ, FQ || AC. Следовательно, трёхвершинники AFE и СQМ удовлетворяют теореме Дезарга.

Следовательно, точки B = AF Ç CQ, D = AE Ç CM и точка О пересечения непараллельных сторон трапеции и FE и QM лежат на одной прямой, то есть точка О лежит на прямой BD.

Два треугольника АВС и DВС пересечены тремя параллельными прямыми p, q, r, r = (АD), p Ç (АВ) = М, p Ç (DВ) = Р, q Ç (АС) = N, q Ç (DC) = Q. Доказать, что прямые (МN), (РQ), (ВС) принадлежат одному пучку.

Рассмотрим два трехвершинника МАN и РDQ (см. рис. 29). По теореме Дезарга, (МN) Ç (РQ) = О, ОВС, следовательно, (МN) Ç (РQ) Ç (ВС) = О. То есть (МN), (РQ), (ВС) принадлежат одному пучку.

Задачи для самостоятельного решения

1. На чертеже ограниченных размеров заданы точка А и пара прямых p и q, пересекающихся за пределами чертежа (в недоступной точке В). Построить доступную часть прямой (АВ).

2. С помощью одной линейки через данную точку А провести прямую параллельную двум заданным параллельным прямым p и q.

3. На евклидовой плоскости даны параллелограмм ABCD, точка М, принадлежащая одной из сторон параллелограмма и прямая n. Пользуясь одной линейкой, провести прямую через точку М параллельно прямой n.

4. Даны прямая n и не лежащие на ней точки M и N. Пользуясь одной линейкой, построить точку пересечения прямой n с MN, не строя прямой MN.

6. Трапеция ABCD пересечена прямыми p и q, параллельными основанию AB, p Ç (AD) = M, p Ç (AC) = P, q Ç (BD) = N, q Ç (BC) = Q. Доказать, что точка (MN) Ç (PQ) лежит на (AB).

7. Используя теорему Дезарга, доказать, что медианы треугольника пересекаются в одной точке.

🌟 Видео

Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

10 класс, 5 урок, Параллельность трех прямыхСкачать

10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Точка, прямая и отрезок. 1 часть. 7 класс.Скачать

7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

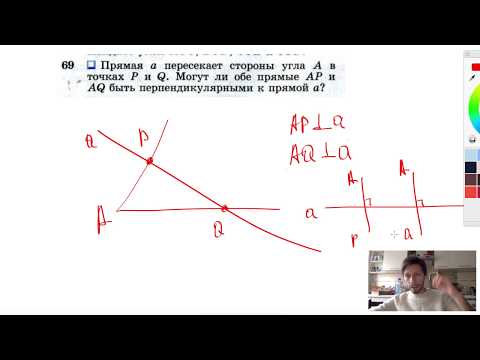
№69. Прямая а пересекает стороны угла А в точках Р и Q. Могут ли обе прямые АР и AQСкачать

10 класс, 14 урок, Задачи на построение сеченийСкачать