Данный угол бас изображен на рисунке 86 проведем окружность (2 видео)

Построить биссектрису данного угла

Скачать
презентациюРассмотрим треугольники АСЕ и АВЕ >>

Задача. Построить биссектрису данного угла. Решение Данный угол ВАС изображен на рисунке. Проведем окружность произвольного радиуса с центром в вершине А. Она пересечет стороны угла в точках В и С. Затем проведем две окружности одинакового радиуса ВС с центрами в точках B и С. Они пересекутся в двух точках. Ту из этих точек, которая лежит внутри угла ВАС, обозначим буквой Е. Докажем, что луч АЕ является биссектрисой данного угла ВАС.

Слайд 9 из презентации «Геометрические задачи на построение». Размер архива с презентацией 2014 КБ.

Содержание

Геометрия 7 класс
Треугольник вписанный в окружность
Определение
Формулы
Радиус вписанной окружности в треугольник
Радиус описанной окружности около треугольника
Площадь треугольника
Периметр треугольника
Сторона треугольника
Средняя линия треугольника
Высота треугольника
Свойства
Доказательство
Данный угол бас изображен на рисунке 86 проведем окружность
📸 Видео

Видео:Построение биссектрисы углаСкачать

Геометрия 7 класс

«Начальные сведения геометрии» — Учёные- геометры. (Около 365-300 до н.э). Введение в геометрию. (1792-1856). Стереометрия. Взаимное расположение точек, прямой и отрезка. Оглавление. Евклид. Геометрические фигуры. Свойство прямой. (Около 570-500до н.э). Пифагор. Сколько точек пересечения могут иметь три прямые ? Планиметрия. Практические задания Взаимное расположение прямых на плоскости Практические задания. История возникновения геометрии.

«Параллельны ли прямые» — Рядом идущие. Вопросы. Папп. Посидоний. Замыкание. Способ построения. Свести параллели к схождению. Способ. Мужская голова. Определения параллельных прямых. Способ построения параллельных прямых. Николай Иванович Лобачевский. Недостаток информации. Построения параллельных прямых. Прямые, лежащие в одной плоскости. Параллельные прямые. Значимость параллельных прямых. Гипотеза. Аксиома параллельных прямых.

«1 признак равенства треугольников» — Равенство треугольников. Историческая справка. Какое еще условие должно быть выполнено. Треугольники, изображенные на рисунке. Ребусы. Треугольники АВС и ACD равны. Треугольники, изображенные на рисунке, равны. Треугольник. Треугольники равны. Первый признак равенства треугольников. Тестирование. Цели урока. Минутка отдыха. План урока. Самостоятельная работа. Найдите по рисунку величину угла АDС и длину стороны ВС.

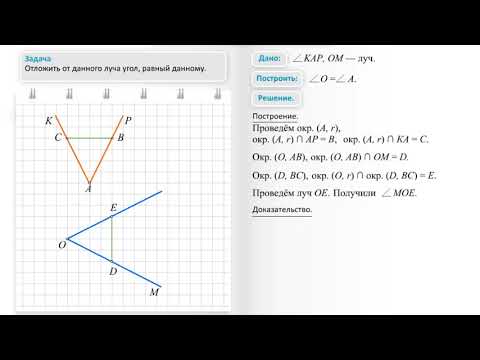
«Геометрические задачи на построение» — Отложить от данного луча угол, равный данному. Рассмотрим треугольники АВС и ОDЕ. Через вершину угла А и точку пересечения окружностей Е проведем прямую. Практические задания по группам. Построение перпендикулярных прямых. Строка параметров включает в себя кнопки состояния полей и сами поля. Медиана РМ равнобедренного треугольника. Построение прямоугольника в ручном режиме. Построить окружность с центром в точке В и с радиусом АВ.

«Свойства и признаки равнобедренного треугольника» — Установка. Равнобедренный треугольник. Медианы. Найдите угол. Девиз нашего урока. Биссектриса треугольника. Контрольные вопросы. Биссектрисы. Две стороны и угол между ними. Два перпендикуляра. Построение циркулем и линейкой. Понятие «свойство». Равносторонний треугольник. Треугольник. Высота. Углы при основании. Качество. Сумма углов треугольника. Исследовательская работа. Свойства треугольников. Достройте треугольник своего настроения.

««Измерение углов» 7 класс» — Измерение углов. Найдите угол, образованный биссектрисами углов. Лучи с общим началом в точке О. Луч OV является биссектрисой угла ZOY. Решение задач. Измерим величину угла АОВ. Свойства углов. Решение задач по готовым чертежам. Как строятся и измеряются углы с помощью транспортира. Виды углов.

Всего в теме «Геометрия 7 класс» 55 презентаций

Видео:Построение биссектрисы угла. 7 класс.Скачать

Треугольник вписанный в окружность

Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Построение угла, равного данному. 7 класс.Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

Периметр треугольника вписанного в окружность,
если известны все стороны:

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

Средняя линия треугольника вписанного
в окружность, если известно основание:

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

Высота треугольника вписанного в окружность,
если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Построение биссектрисы углаСкачать

Свойства

Центр вписанной в треугольник окружности
находится на пересечении биссектрис.
В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну.
Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора.
Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров.
Все вершины треугольника, вписанного
в окружность, лежат на окружности.
Сумма всех углов треугольника — 180 градусов.
Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.

Видео:7 класс, 23 урок, Примеры задач на построениеСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

Проведем серединные
перпендикуляры — HO, FO, EO.
O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника.
Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Задачи на построение с помощью циркуля и линейки - 7 класс геометрияСкачать

Данный угол бас изображен на рисунке 86 проведем окружность

Найдите тангенс угла AOB, изображенного на рисунке.

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

На квадратной сетке изображён угол A. Найдите .

Опустим перпендикуляр BH. Треугольник ABH — прямоугольный. Таким образом,

Найдите тангенс угла, изображённого на рисунке.

Углы и в сумме образуют развёрнутый угол Значит,

Рассмотрим прямоугольный треугольник, изображённый на рисунке. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: