Дана окружность с центром в точке о 4 точки

Ответ:

Объяснение:

CZ⊥GC, значит GZ — диаметр. (Вписанный угол, опирающийся на диаметр, — прямой)

По условию CK=GZ, значит СК — тоже диаметр.

Значит вписанные углы CGKZ — прямоугольник.

Видео:№640. Даны окружность с центром О радиуса 4,5 см и точка А. Через точку А проведены две касательныеСкачать

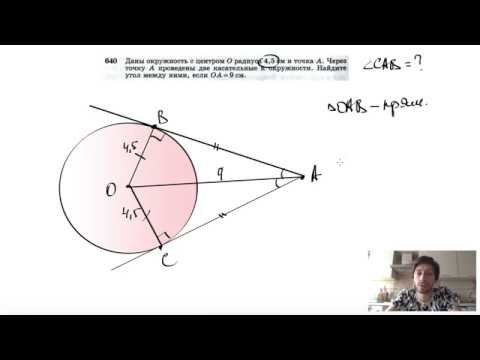
Планиметрия. Страница 3

Видео:2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

1.Окружность

Окружностью называется фигура, состоящая из множества точек на плоскости, равноудаленных от данной точки.

Эта данная точка называется центром окружности. Расстояние от центра окружности до ее точек называется радиусом окружности.

Отрезок, соединяющий две точки окружности, называется хордой.

Если хорда проходит через центр окружности, то она называется диаметром. (Рис.1)

ОА — радиус
ВС — диаметр
DE — хорда

Рис.1 Окружность, радиус, диаметр, хорда.

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

2.Окружность, описанная около треугольника

Теорема: центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров, опущенных на середины сторон данного треугольника.

Доказательство. Пусть АВС данный треугольник и точка О является центром окружности, описанной около данного треугольника. (Рис.2) Тогда отрезки ОА, ОВ, ОС равны как радиусы. Следовательно, треугольники Δ АОВ, Δ ВОС, Δ АОС — равнобедренные. А следовательно, и медианы, проведенные к серединам сторон ОК, ОЕ, ОD, являются одновременно биссектрисой и высотой. Поэтому предположение, что центр окружности, описанной около треугольника, является точкой пересечения высот, верно.

Рис.2 Теорема. Окружность, описанная около треугольника.

Видео:Урок 3. №23 ОГЭ. Касательная. Окружность с центром на стороне AC касается АВ в точке В.Скачать

3.Окружность, вписанная в треугольник

Теорема. центр окружности, вписанной в треугольник, является точкой пересечения биссектрис, проведенных из его углов.

Доказательство. Пусть дан треугольник АВС. Точка О — центр вписанной окружности. (Рис. 3)

Тогда треугольник Δ АОЕ равен треугольнику Δ АОТ,
Δ СОЕ = Δ СОК,
Δ ВОК = Δ ВОТ.
Так как стороны ОА, ОВ, ОС у них общие. А ОК, ОЕ, ОТ как радиусы.
Следовательно:
∠ ЕАО = ∠ ТАО,
∠ ЕСО = ∠ КСО,
∠ КВО = ∠ ТВО.

Это значит, что точка О лежит на пересечении биссектрис АО, ВО, СО.

Рис.3 Теорема. Окружность, вписанная в треугольник.

Видео:На окружности с центром O отмечены точки A и B так ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

4.Геометрическое место точек

Геометрическое место точек это фигура, которая представляет собой совокупность точек на плоскости, подчиняющихся определенному закону или обладающих определенным свойством.

Теорема. Геометрическим местом точек называется прямая, все точки которой равноудалены от двух данных точек, перпендикулярная отрезку, соединяющему эти точки и проходящая через его середину.

Доказательство. Пусть дан отрезок АС. Прямая А проходит через середину этого отрезка и перпендикулярна ему.(Рис. 4).

Тогда треугольники Δ АМВ и Δ СМВ равны. Так как сторона ВМ у них обшая, а стороны АМ и МС равны по условию. Следовательно точка В равноудалена от точек А и С.
Возьмем другую точку, например D, не лежащую на прямой а. Тогда сторона MD не принадлежит прямой а. А следовательно, углы AMD и DMC не равны т.к. не равны треугольники. Данное утверждение основано на том, что через точку, лежащую на прямой, можно провести только одну перпендикулярную ей прямую. И следовательно, расстояния от точки D до точек А и С не равны. Поэтому, для того чтобы расстояния от некой точки Х до двух данных точек были равны, необходимо чтобы она лежала на прямой а, которая перпендикулярна отрезку, соединяющего эти точки, и которая проходит через его середину.

Рис.4 Теорема. Геометрическое место точек.

Репетитор: Васильев Алексей Александрович

Предметы: математика, физика, информатика, экономика, программирование.

2000 руб / 120 мин — подготовка к ЕГЭ и ГИА для школьников. 3000 руб / 120 мин — индивидуально (базовый уровень). 2000 руб / 120 мин — студенты.

Тел. 8 916 461-50-69, email: alexey-it@ya.ru

Пример 1

Дана окружность с центром О. И проведена касательная а из точки С к этой окружности. Доказать, что точка К лежит на основании равнобедренного треугольника ОВС, если OB = 2R. (рис.5)

По условию прямая а есть касательная к окружности, следовательно радиус, проведенный к точке касания ОК, и который лежит на прямой с, составляет прямой угол с касательной. Так как ОВ = 2R и KB = R, то прямая а будет представлять собой геометрическое место точек, так как она перпендикулярна отрезку ОВ и проходит через его середину. А следовательно, треугольники ВКС и ОКС равны по первому признаку равенства треугольников. Отсюда можно сделать вывод, что точка К будет лежать на основании равнобедренного треугольника ВОС.

Рис.5 Задача. Дана окружность с центром О.

Пример 2

Докажите, что касательная к окружности не имеет с ней других общих точек, кроме точки касания. (Рис.6)

Доказательство:

Пусть дана окружность с центром в точке О. И прямая а, которая касается окружности в точке А. Допустим, что прямая а имеет еще одну точку касаная — точку В. Тогда радиус окружности, проведенный к точкам А и В образует угол с прямой а равный 90°.

Таким образом, в равнобедренном треугольнике АОВ углы при вершинах А и В равны 90°. А это невозможно. Следовательно, мы пришли к противоречию и прямая а не может касаться окружности в двух точках.

Рис.6 Задача. Касательная к окружности.

Пример 3

Точки А,В,С лежат на одной прямой, а точка О лежит вне этой прямой. Докажите, что треугольники АОВ и ВОС не могут быть равнобедренными с основаниями АВ и ВС. (Рис.7)

Доказательство:

Допустим, что треугольники АОВ и ВОС равнобедренные с основаниями АВ и ВС. Тогда Стороны АО, ВО и СО равны. Отсюда следует, что углы ОАВ, АВО, ОВС и ОСВ равны. И ∠АВО = ∠ОВС = 90°, так как эти углы являются смежными, а их сумма равна 180°.

Таким образом, в равнобедренных треугольниках АОВ и ВОС углы при вершинах А и С равны 90°. А это невозможно, потому, что тогда стороны АО, ВО и СО были бы параллельны, так как они перпендикулярны одной прямой АС. Следовательно, мы пришли к противоречию, и треугольники АОВ и ВОС не могут быть равнобедренными с основаниями АВ и ВС.

Рис.7 Задача. Даны три точки на прямой.

Пример 4

Окружности с центрами О и О₁ пересекаются в точках А и В. Докажите, что прямая АВ перпендикулярна прямой ОО₁ (Рис.8)

Доказательство:

Так как окружности пересекаются в точках А и В, то эти две точки принадлежат обеим окружностям. Следовательно, отрезок ОА = ОВ, как радиусы окружности с центром в точке О. А отрезок О₁А = О₁В, как радиусы окружности с центром в точке О₁.

Таким образом, треугольники ОАО₁ и ОВО₁ равны по третьему признаку равенства треугольников (по трем сторонам). А следовательно отрезки АС и ВС равны. И прямая ОО₁ является геометрическим местом точек для двух данных точек А и В. Т.е. любая точка прямой ОО₁ равноудалена от двух данных точек А и В. Следовательно, треугольники ОАС и ОВС равны, также как и треугольники АСО₁ и ВСО₁ по трем сторонам. А отсюда следует равенство углов при вершине С. Т.е. ∠ОСА = ∠ОСВ = ∠АСО₁ = ∠ВСО₁ = 90°.

Следовательно, можно сделать вывод, что прямая АВ перпендикулярна прямой ОО₁.

Рис.8 Задача. Окружности с центрами О и О₁.

Пример 5

Отрезок ВС пересекает прямую а в точке О. Расстояние от точек В и С до прямой а равны. Докажите, что точка О является серединой отрезка ВС (Рис.9)

Доказательство:

По условию задачи, расстояния от точек В и С до прямой а равны. Т.е. РС = BQ. Так как расстояние от точки до прямой представляет собой перпендикуляр, то два треугольника РОС и ВОQ, образованные двумя пересекающимися прямыми ВС и а, и перпендикулярами, опущенными на одну из них, равны по второму признаку равенства треугольников ( по стороне и двум прилегающим к ней углам: РС = BQ, углы при вершинах В и С равны как внутренние накрест лежащие, а углы при вершинах Р и Q прямые).

Из равенства треугольников РОС и ВОQ следует, что ВО = ОС.

Рис.9 Задача. Отрезок ВС пересекает прямую а .

Видео:2034 треугольник ABC вписан в окружность с центром в точке O точки O и C лежат в одной полуплоскостиСкачать

Окружность с центром в точке О(0 ; 4) проходит через точку К(4 ; 1) а)запишите уравнение этой окружности б)найдите точки окружности, которые имеют абсциссу, равную 3?

Геометрия | 5 — 9 классы

Окружность с центром в точке О(0 ; 4) проходит через точку К(4 ; 1) а)запишите уравнение этой окружности б)найдите точки окружности, которые имеют абсциссу, равную 3.

Уравнение окружности (x — a) ^ 2 + (y — b) ^ 2 = R ^ 2 где (a ; b) — центр окружности радbec находим также по формуле длине отрезка ОК = R = V(0 — 4) ^ 2 + (4 — 1) ^ 2 = 5

тогда уравнение окружности принимет вид

х ^ 2 + (y — 4) ^ 2 = 5.

Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Через точку А к окружности проведены касательная АВ (точка В лежит на окружности) и секущая, которая пересекает окружность в точках Е и F и проходит через центр окружности?

Через точку А к окружности проведены касательная АВ (точка В лежит на окружности) и секущая, которая пересекает окружность в точках Е и F и проходит через центр окружности.

Найти радиус окружности, если АВ = 12 , а АF = 18.

Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Через точку A к окружности проведены AB (точка B лежит на окружности) и секущая, которая пересекает окружность в точках E и F и проходит через центр окружности?

Через точку A к окружности проведены AB (точка B лежит на окружности) и секущая, которая пересекает окружность в точках E и F и проходит через центр окружности.

Найдите радиус окружности, если AB = 12, AF = 18 /.

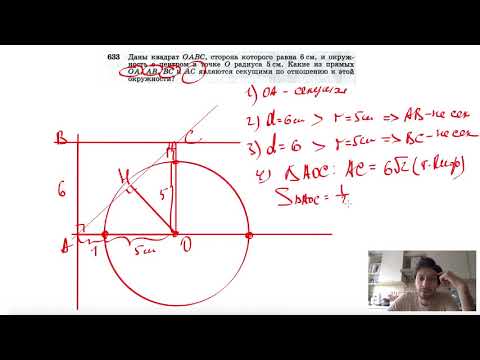
Видео:№633. Даны квадрат ОАВС, сторона которого равна 6 см, и окружность с центром в точке О радиуса 5 см.Скачать

Составьте уравнение окружности с центром в точке А( — 3, 4) касающейся оси абсцисс?

Составьте уравнение окружности с центром в точке А( — 3, 4) касающейся оси абсцисс.

Видео:Точка М лежит на диаметре АВ окружности с центром ОСкачать

Окружность с центром в точке О(0, 4)проходит через точку К(4, 1)запишите уравнение этой окружности?

Окружность с центром в точке О(0, 4)проходит через точку К(4, 1)запишите уравнение этой окружности.

Найдите точки окружности которые имеют абсциссу равную 3.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Помогие пожааааааааааалуйста?

Даны точки А( — 7 ; — 3) и М( — 4 ; 1).

Точка М — середина отрезка АВ.

А) Найдите координаты второго конца отрезка АВ.

Б) Найдите длину отрезка АВ.

№2. Окружность с центром в точке О(0 ; 4) проходит тчерез точку К(4 ; 1).

А) Запишите уравнение этой окружности б) Найдите точки окружности, которые имеют абсциссу, равную 3.

№3. Дана окружность с центром в точке О, заданная уравнением (х — 2) ^ 2 + (у + 1) ^ 2 = 4.

Докажите, что данная окружность проходит через середину отрезка ОА.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Из точки А к окружности с центром в точке О проведена касательная, которая касается окружности в точке В?

Из точки А к окружности с центром в точке О проведена касательная, которая касается окружности в точке В.

Найдите радиус окружности, если АВ = 8см, АО = 17см.

Видео:№962. Даны окружность х2 + у2 = 25 и две точки А(3; 4) и В (4; -3).Скачать

Найдите уравнение окружности , которая проходит через точку F(5, — 2) и центр который находится в точке С ( — 1, 1)?

Найдите уравнение окружности , которая проходит через точку F(5, — 2) и центр который находится в точке С ( — 1, 1).

Видео:Из точки A проведены две касательные к окружности ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Составьте уравнение окружности с центром в точке (2 ; — 1), которое проходит через точку м ( — 2 ; 2)?

Составьте уравнение окружности с центром в точке (2 ; — 1), которое проходит через точку м ( — 2 ; 2).

Видео:Уравнение окружности (1)Скачать

Напиши уравнение окружности, которая проходит через точку 10 на оси Ox и через точку 4 на оси Oy если известно, что центр находится на оси абсцисс?

Напиши уравнение окружности, которая проходит через точку 10 на оси Ox и через точку 4 на оси Oy если известно, что центр находится на оси абсцисс.

Видео:№644. Прямые МА и MB касаются окружности с центром О в точках А и В. Точка С симметрична точке ОСкачать

Если расстояние от точки до центра окружности меньше или равно радиусу окружности, то эта точка лежит на окружности?

Если расстояние от точки до центра окружности меньше или равно радиусу окружности, то эта точка лежит на окружности?

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Окружность с центром в точке О(0 ; 4) проходит через точку К(4 ; 1) а)запишите уравнение этой окружности б)найдите точки окружности, которые имеют абсциссу, равную 3?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Мама за 30 минут прошла 2, 5 км, Юра проехал 6 км. Имеем прямоугольный треугольник с катетами 2, 5 и 6 км. Надо найти гипотенузу. С² = 2, 5² + 6² = 6, 25 + 36 = 72, 25 с = √72, 25 = 8, 5 Ответ : 8, 5 км.

Вот 180 — (65 + 50) = 65 и т. Д На фото.

По — моему, есть ошибка в вопросе.

Пусть х — один из смежных углов, тогда второй угол 180 — х. Биссектриса первого угла — х / 2, второго — (180 — х) / 2 = 90 — (x / 2). Т. к. Биссектрисы выходят из одной точки то угол между ними равен (х / 2) + 90 — (х — 2) = 90. Следовательно, би..

126 градусов, 76 + 50 = 126.

АОВ + ВОР = 76 + 50 = 126 поплидмзмшь.

Розв»язок додала. Вiдповiдь 112см².

10 : 2 = 5 25 : 2 = 12, 5 5 ^ 2 + 12, 5 ^ 2 = 13, 462 ^ 2 13, 462 * 4 = 53, 848.

260 ответ там формула такая.

Какой вопрос? Как ответить если нет вопроса.

📹 Видео

Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

ОГЭ по математике. Треугольник вписан в окружность . (Вар. 4) √ 17 модуль геометрия ОГЭСкачать

Условие принадлежности четырёх точек одной окружностиСкачать

В угол C величиной 83° вписана окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать