Что такое смежные треугольники

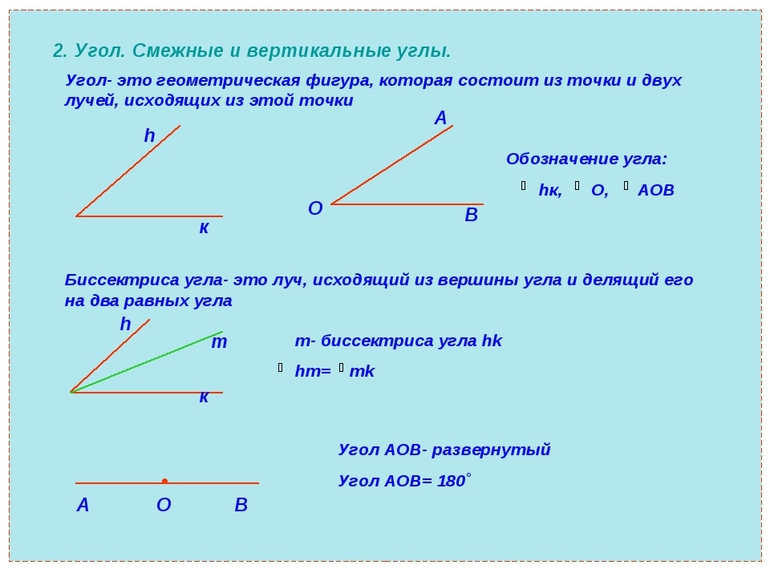
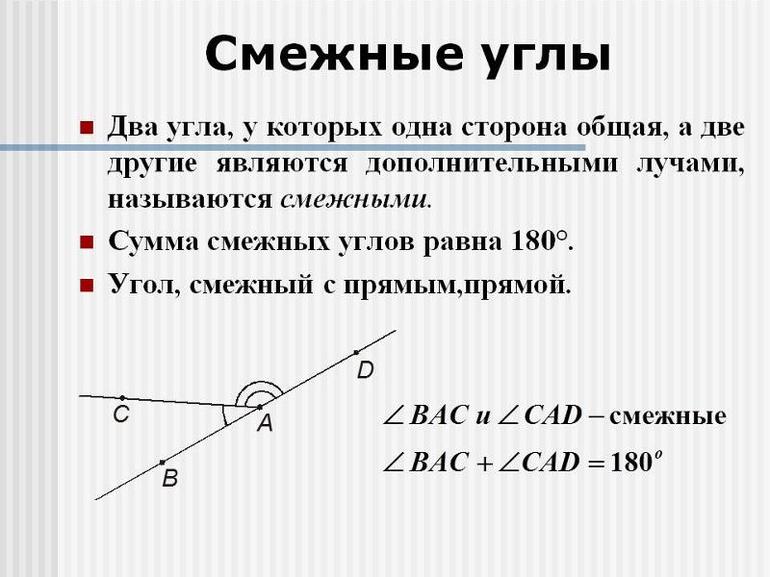
Определение 1. Смежными называются два угла, у которых одна сторона общая, а другие стороны являются продолжениями друг друга.

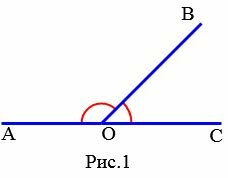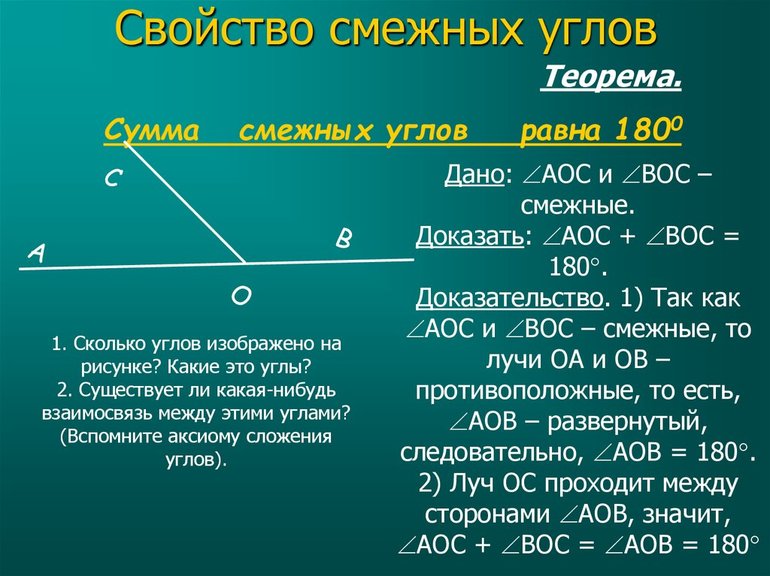
На Рис.1 углы AOB и BOC смежные, так как сторона OB общая для этих углов, а стороны OA и OC являются продолжениями друг друга. Поскольку угол AOC является развернутым углом, то сумма смежных углов равна 180°:

.

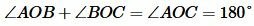(1)

Видео:7 класс, 11 урок, Смежные и вертикальные углыСкачать

Свойства смежных углов

1. Сумма смежных углов равна 180°

2. Если оба смежных угла равны между собой, то они являются прямыми.

3. В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.

4. Синусы смежных углов равны.

5. Косинусы, тангенсы и котангенсы смежгых углов равны, но имеют противоположный знак.

Справедливость пунктов 2 и 3 очевидны и следуют из (1).

Доказательство пункта 4. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но (см. статью Формулы приведения тригонометрических функций онлайн)

.

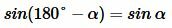То есть синусы смежных углов равны.

Доказательство пункта 5. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но

,

,

.

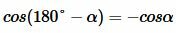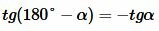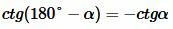То есть косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Смежные углы — признаки, свойства и теоремы

Видео:Смежные углы. 7 класс.Скачать

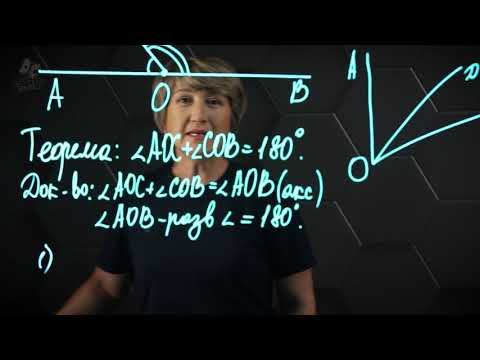
Общие сведения

Основными элементами, используемыми в геометрии, являются лучи и углы. С их помощью образуется любая геометрическая фигура — квадрат, треугольник или любого вида многоугольник. Луч — это полупрямая, то есть часть линии, на которой точки располагаются по одной стороне от зафиксированной. По-другому можно сказать, что луч — это линия, ограниченная только с одной стороны. Обозначают его как прописными латинскими буквами, так и заглавными с названием точек. Во втором случае первой указывается начальная точка.

Два луча, выходящие из одной точки, образовывают угол. По сути, это незамкнутая геометрическая фигура. Она имеет вершину (общую точку) и стороны. Обозначают его с помощью трёх заглавных букв, соответствующих трём точкам — вершине и двум лежащим на разных сторонах лучах. Внутренняя часть формируется из множества точек, принадлежащих плоскости, ограниченной сторонами угла.

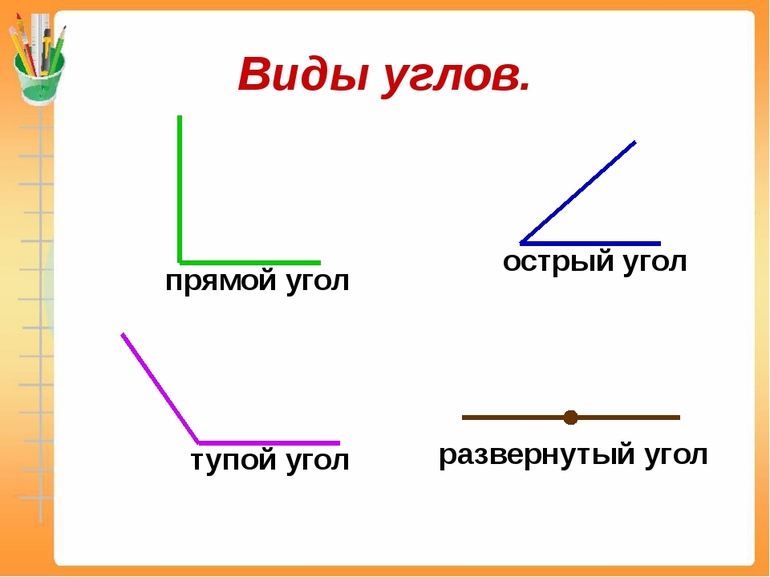
Существует шесть видов углов:

• Острый — расстояние между сторонами составляет меньше 90 градусов.
• Прямой — образовывается двумя взаимно перпендикулярными прямыми.
• Тупой — разворот угла больше 90 градусов, но не превышает 180.
• Развёрнутый — представляет сумму двух прямых элементов.
• Выпуклый — угол между лучами составляет больше 180 градусов, но меньше 360.
• Полный — равняется 360 градусам.

Располагаясь на плоскости, по отношению друг к другу углы могут быть смежными или вертикальными. Согласно определению, смежными углами называют такую пару, у которой одна сторона принадлежит обеим фигурам, а два других луча образуют прямую линию. Вертикальными же считаются углы, стороны которых дополняют друг друга до прямых линий. Они всегда градусно равны.

Из угла всегда можно провести линию, делящую его на две равные части. Такой луч, исходящий из вершины, называют биссектрисой. А это значит, что после его проведения образуется два равных смежных угла, обладающих одинаковыми свойствами.

Единицей измерения разворота фигуры является градусная мера. Если в нём содержится нецелое количество градусов, то используются минуты и секунды. Так, в одном градусе содержится 60 минут, а в одной минуте 60 секунд.

Видео:№192. В треугольнике ABC угол А равен 40°, а угол BCE, смежный с углом ACB, равен 80°Скачать

Основные факты

Вычисление элементов треугольников используется в географии, строительстве, астрономии, мореплавании и других науках и технике, например, кинематике, механике, оптике, при проведении гармонического анализа. Для успешного решения задач по теме нужно знать следующие факты:

1. При пересечении двух лучей образуются стороны, которые являются продолжением друг друга, при этом образованные угловые элементы будут вертикальными.
2. Сумма угловых частей в треугольнике при сложении составляет 180 градусов.
3. Биссектрисы смежных частей взаимно перпендикулярны.
4. Если существуют односторонние угловые элементы, то при параллельных линиях они будут перпендикулярными.
5. Если точка располагается на равноудалённом расстоянии от угловой стороны, то она находится на биссектрисе.
6. Равнобедренным называют треугольник с двумя равными сторонами, при этом высота и медиана у него совпадают. Отсюда следует, что два угла в такой фигуре равны.
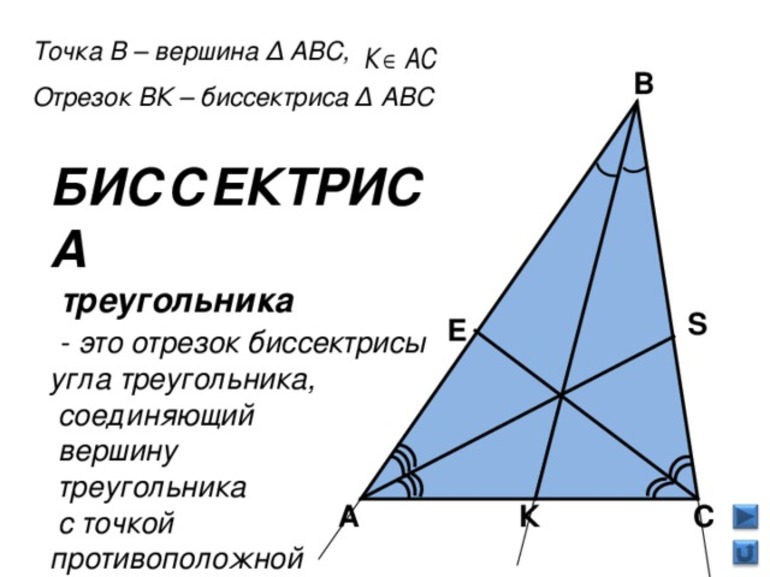
7. Биссектриса треугольника делит противоположную сторону на части, пропорциональные прилегающим сторонам.
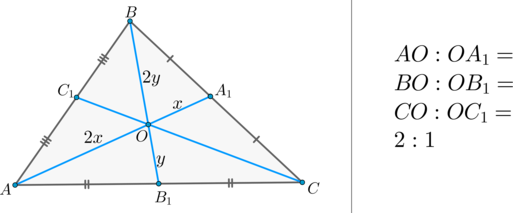
8. Точка пересечения медиан в треугольнике делит их в отношении один к двум, начиная отсчёт от вершины.
9. Медиана, построенная из вершины прямого угла, равняется одной второй гипотенузы.
10. Высота в треугольнике делит его на две фигуры, подобные начальной.
11. Средняя линия треугольника представляет вектор, состоящий из середин двух его сторон, при этом она параллельна третьей стороне и отсекает от фигуры подобный треугольник.
12. Катет, примыкающий к вершине угловой части объекта, называется прилежащим и формирует его совместно с гипотенузой. Другой же луч, не примыкающий к элементу, находится напротив вершины и является противолежащим.
13. Синусом называется отношение противолежащего катета к гипотенузе, а косинусом — отношение прилежащего к угловому элементу катету к гипотенузе.

Кроме этого, нужно учесть, что отличие смежных углов от вертикальных заключается в том, что сумма первых равняется 180 градусам, а вторые всегда равняются друг другу.

Иными словами, для пары углов смежным будет угловой элемент, равный у = (180 — x) градусам. Причём при пересечении двух лучей получается четыре смежные пары, из которых две будут вертикальными. Это основополагающие факты, на которых построена геометрия и тригонометрия. Зная их, можно переходить к изучению таких сложных наук, как, например, планиметрия и стереометрия.

Видео:Смежные и вертикальные углы. Практическая часть - решение задачи. 7 класс.Скачать

Свойства и теорема

С теоремой о смежных углах знакомят на уроках геометрии в седьмом классе средней школы. Исходя из того, что такие фигуры имеют общую вершину и сторону, можно предположить, что сумма углов будет равняться 180 градусам. При этом каждый из них способен дополнить другой до развёрнутого. Равенство суммы 180 градусам и является основной теоремой.

Доказательство этого утверждения выполняется довольно просто. Делается это путём изображения пары смежных углов ABC и CBK. Вершина располагается в точке B, а сторона BC является общей. Изучив рисунок, можно отметить, что стороны AB и BK лежат на одной прямой. По аксиоме измерения углов получается, что ∠ABC + ∠СBK = ∠ABK. Иными словами, полученные углы образовывают развёрнутый, то есть такой, значение которого равняется 180 градусам. Формулой теорему можно записать как ∠ABC + ∠CBK = 180 0 .

На основании рассмотренной теоремы вытекают три свойства смежных углов:

• если они равны, то они являются прямыми;
• угол, смежный с тупым, — острый, и наоборот;
• когда два угла равны, то будут равными и смежные с ними развороты.

А также существуют следствия или, как их ещё называют, тригонометрические соотношения. В их основе лежит то, что косинусы и тангенсы рассматриваемых фигур всегда будут равны по величине, но противоположны по знаку. При этом если необходимо построить угол, смежный с существующим, то нужно одну из сторон продлить за вершину.

Указанные свойства используются и при определении подобия треугольников. Например, согласно первому признаку, если два угла равностороннего или разностороннего треугольника совпадают с двумя углами другого, то они подобны. Случается, что по одну сторону от линии могут находиться несколько лучей, имеющих общую вершину. Изобразив такую ситуацию на чертеже, легко убедиться, что если все полученные углы сложить, то их сумма будет соответствовать значению двух прямых, а также из них всегда можно образовать смежную пару.

Этот свойство используется тогда, когда необходимо определить, чему равняется сумма углов вокруг конкретно взятой вершины. То есть продолжив одну из сторон за рассматриваемую вершину, можно получить две группы: первую — сумма которых равна двум прямым, и вторую — сумма которых также равна двум прямым углам. Отсюда следует, что сумма вокруг общей вершины будет равняться прямым углам.

Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Примеры решения задач

Решать задачи по заданной теме проще, если выполнять чертежи. С их помощью, а также зная свойства и теоремы, найти правильный ответ не составит особого труда. Существуют типовые задания, позволяющие закрепить пройденный материал и на практике применить полученные знания. Вот наиболее интересные из них с подобным решением:

1. Возможно ли существование такой смежной пары, в которой будут два остроугольника? Для ответа на вопрос нужно рассуждать следующим образом. Острым называется такой элемент, разворот которого меньше 90 градусов. Так как пара должна содержать общую сторону, то второй элемент будет тупоугольным. Исключением будет, если из вершины лучи выходят перпендикулярно друг другу, поэтому существование такой пары невозможно.
2. Один из парных элементов меньше другого на 80 градусов, необходимо найти разворот второго. Итак, если первый угол принять равным U, то второй, согласно условию, будет равняться U — 80. Так как в сумме они оба дают 180 градусов, то верным будут следующие уравнения: U + U + 66 = 180; 2 * U = 180 — 80; 2 * U = 100; U = 100/2 = 50. Отсюда разворот второго элемента составит: 50 + 80 = 130 градусов.
3. Имеются два прямоугольных треугольника со смежными между собой углами, при этом их меры в градусах относятся как 2:3. Чтобы найти их значения, нужно вспомнить, что сумма смежных углов равна 180 градусам. Обозначив первый разворот два икс, а второй с коэффициентом три, справедливо будет записать: 2x + 3x = 180. Решив уравнение, можно определить икс, его значение будет равняться: x = 30. Затем, подставив вместо икса его численную величину, довольно просто вычислить ответ. Искомые значения будут 60 и 90 градусов.
4. Восьмая часть одного из смежных элементов и три четверти другого составляют в сумме прямую фигуру. Нужно найти разность. Так как сумма парных углов 180°, то пусть один из них равняется икс, тогда другой будет игрек. На основании этих данных можно составить систему: x + y = 180; x / 8+ (3у) / 4 = 90. Сложив оба уравнения, можно получить равенство: x + 6y = 720; 5y = 540. Отсюда: y = 108°, x = 180 — 108 = 72 градуса. В итоге искомая разность составит: 108 — 72 = 36.

Уметь правильно решать задачи важно, так как в дальнейшем эти знания помогают находить такие важные элементы, как площадь треугольника, зная только разворот и высоту произвольной фигуры, а далее уже легко будет вычислить и объём. Кроме этого, правила смежности часто используются в тригонометрии при нахождении синусов и косинусов.

Видео:Геометрия 7 класс (Урок№6 - Смежные и вертикальные углы. Аксиомы и теоремы.)Скачать

Вычисление на онлайн-калькуляторе

Нахождение градусной меры смежных элементов обычно не вызывает проблем и относится к элементарным действиям при исследованиях различных треугольников, например, остроугольных или равнобедренных. Но при работе с нецелыми числами или в процессе обучения имеет смысл использовать так называемые онлайн-калькуляторы.

Это обычные интернет-сайты, содержащие встроенную программу для автоматических расчётов. Пользоваться ими сможет каждый, кто имеет компьютер или гаджет с установленным веб-обозревателем. Вся работа с сервисом сводится к загрузке его интернет-страницы и заполнения специальной формы, в которую вводятся исходные данные. Затем нажимается интерактивная кнопка и на дисплее появляется ответ.

Вычисление обычно занимает пару секунд, а появление ошибки исключено. Кроме этого, на сайтах, предлагающего такого рода услуги, содержится весь необходимый для расчётов теоретический материал. Поэтому даже слабо подготовленный по теме пользователь сможет понять, откуда и каким образом получился тот или иной ответ.

Из множества сервисов, существующих в русскоязычном сегменте всемирной сети, можно выделить следующие:

Эти сервисы доступны бесплатно, имеют интуитивно понятный интерфейс на русском языке.

При этом пользователям предлагается ознакомиться с развёрнутым решением, то есть указан поэтапный расчёт. Для удобства на страницах даётся не только необходимая теория, но и ряд типовых примеров с подробным описанием действий.

Следует отметить, что указанные сервисы могут находить ответ для любой сложности математической задачи. Особенно востребованными становятся такие вычисления в инженерии, связанные с тригонометрическими функциями. Ведь для таких расчётов важны точность и время, что вполне могут обеспечить онлайн-калькуляторы.

Видео:Геометрия 7 класс | Вертикальные, смежные, накрест лежащие и другие углы (теория) | МАТЕМАТИКА 2021Скачать

Смежные и вертикальные углы. Треугольник. Равнобедренный треугольник. Медиана, биссектриса, высота, средняя линия

Готовиться с нами — ЛЕГКО!

Видео:Смежные углыСкачать

Эффективное решение существует!

Вы ищете теорию и формулы для ЕГЭ по математике ? Образовательный проект «Школково» предлагает вам заглянуть в раздел «Теоретическая справка». Здесь представлено пособие по подготовке к ЕГЭ по математике, которое фактически является авторским. Оно разработано в соответствии с программой школьного курса и включает такие разделы, как арифметика, алгебра, начала анализа и геометрия (планиметрия и стереометрия). Каждое теоретическое положение, содержащееся в пособии по подготовке к ЕГЭ по математике, сопровождается методически подобранными задачами с подробными разъяснениями.

Таким образом, вы не только приобретете определенные знания. Полный справочник для ЕГЭ по математике поможет вам научиться логически и нестандартно мыслить , выполнять самые разнообразные задачи и грамотно объяснять свои решения. А это уже половина успеха при сдаче единого государственного экзамена.

После того, как вы нашли необходимые формулы и теорию для ЕГЭ по математике, рекомендуем вам перейти в раздел «Каталоги» и закрепить полученные знания на практике. Для этого достаточно выбрать задачу по данной теме и решить ее. Кроме того, справочные материалы по математике для ЕГЭ пригодятся вам и для других естественнонаучных дисциплин, таких как физика, химия и т. д.

Факт 1.
(bullet) Смежные углы — два угла, имеющие общую сторону, а две другие стороны являются продолжениями одна другой.

Смежные углы: (angle AOB) и (angle BOC) .
Теорема: Сумма смежных углов равна (180^circ) : (angle AOB+angle BOC=180^circ) .

Факт 2.
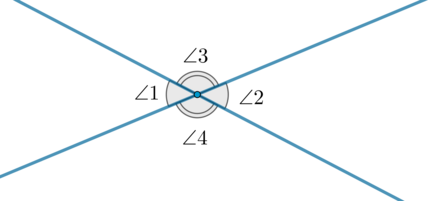
(bullet) Вертикальные углы — два угла, у которых стороны одного угла являются продолжениями сторон другого (образуются, например, при пересечении двух прямых).

Вертикальные углы: (angle 1) и (angle 2) , (angle 3) и (angle 4) .
Теорема: Вертикальные углы равны: (angle 1=angle 2) и (angle 3=angle 4) .

Факт 3.
(bullet) Сумма углов (angle A, angle B, angle C) треугольника (ABC) равна (180^circ) .
(bullet) Внешний угол (angle BCD) треугольника (ABC) равен сумме двух углов треугольника, не смежных с ним.

Факт 4.
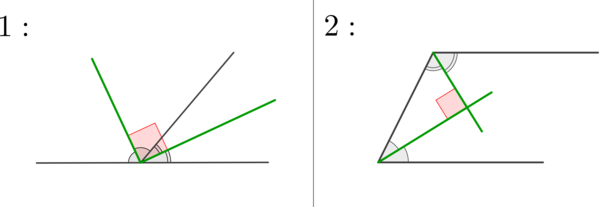
(bullet) Биссектрисы смежных углов взаимно перпендикулярны.
(bullet) Биссектрисы односторонних углов при параллельных прямых взаимно перпендикулярны.

Факт 5.
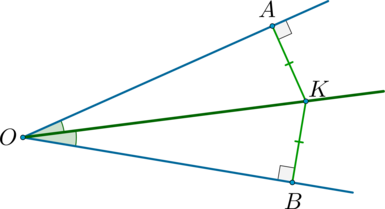
(bullet) Прямая теорема: каждая точка биссектрисы угла равноудалена от сторон угла.
(bullet) Обратная теорема: если точка равноудалена от сторон угла, то она лежит на его биссектрисе.

Факт 6.
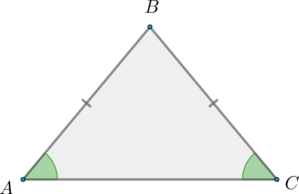
(bullet) Равнобедренный треугольник – треугольник, у которого две стороны равны. Третья сторона треугольника называется основанием.
Первое свойство равнобедренного треугольника:

Второе свойство равнобедренного треугольника: углы при основании равны.

Первый признак равнобедренного треугольника: если у треугольника два угла равны, то он равнобедренный.
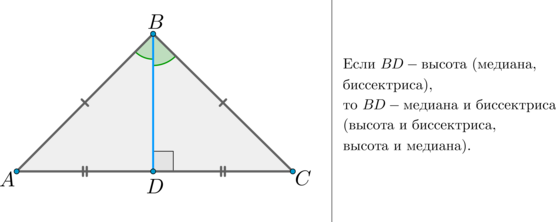
Второй признак равнобедренного треугольника: если у треугольника совпадают высота и медиана (высота и биссектриса или медиана и биссектриса), проведенные к одной и той же стороне, то этот треугольник является равнобедренным.

Факт 7.
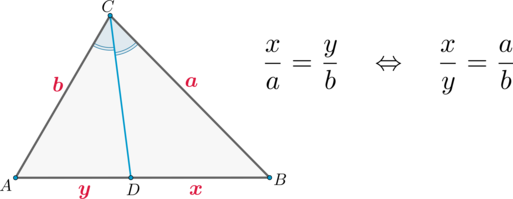
(bullet) Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.

Факт 8.
(bullet) Медианы в треугольнике точкой пересечения делятся в отношении (2:1) , считая от вершины.

Факт 9.
(bullet) Медиана треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.

Факт 10.
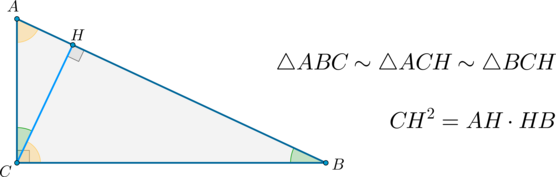
(bullet) Высота, проведенная из вершины прямого угла треугольника, делит его на два треугольника, подобных исходному.
(bullet) Квадрат этой высоты равен произведению отрезков, на которые она делит гипотенузу.

Факт 11.
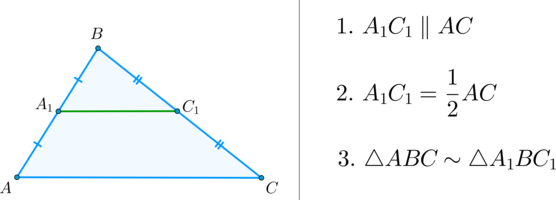
(bullet) Средняя линия треугольника – отрезок, соединяющий середины двух его сторон.
(bullet) 1. Средняя линия треугольника параллельна третьей стороне.
(bullet) 2. Средняя линия треугольника равна половине третьей стороны.
(bullet) 3. Средняя линия отсекает от треугольника подобный ему треугольник.

Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.

Видео:Внешний угол треугольникаСкачать

Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?

1. Потому что это расширяет кругозор . Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.
2. Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.

Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.

📺 Видео

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Сравнение углов. Виды углов. Чертежный треугольник. 5 класс.Скачать

Треугольник и смежные углы | Мир МатематикаСкачать

ЕГЭ база #15 / Треугольники и их элементы / Внешний угол / Смежные углы / решу егэСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Вертикальные углы. 7 класс.Скачать

ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать

ГЕОМЕТРИЯ 7 класс : Соответственные, односторонние и накрест лежащие углыСкачать

СМЕЖНЫЕ ВЕРТИКАЛЬНЫЕ УГЛЫ геометрия 7 класс. Теорема, доказательствоСкачать