Что такое расстояние между векторами (3 видео)

VMath

Содержание

Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Евклидово пространство
Определения
Свойства
Ортогонализация
Матричный формализм алгоритма Грама-Шмидта: QR-разложение
Расстояние от точки до многообразия
Вычисление расстояния
Угол между вектором и линейным многообразием
Свойства матрицы Грама
Задачи
Источник
Линейная алгебра для разработчиков игр
Зачем нам линейная алгебра?
Что такое вектор?
Сложение векторов
Вычитание векторов
Умножение вектора на скаляр
Длина вектора
Расстояние
Нормализация
Скалярное произведение векторов
Векторное произведение
Базисный вектор
Матрицы
Трехмерные матрицы
Вращение в двухмерном пространстве
Трёхмерное вращение
Вращение, определяемое осью и углом (Axis-angle rotation)
Эйлеровские углы
Вращение с помощью матриц
Кватернионы
Векторы. Метод координат. Угол между прямыми, плоскостями. Расстояние от точки до плоскости, между скрещивающимися прямыми
🔥 Видео

Инструменты сайта

Основное

Информация

Действия

Содержание

Видео:Расстояние между точкамиСкачать

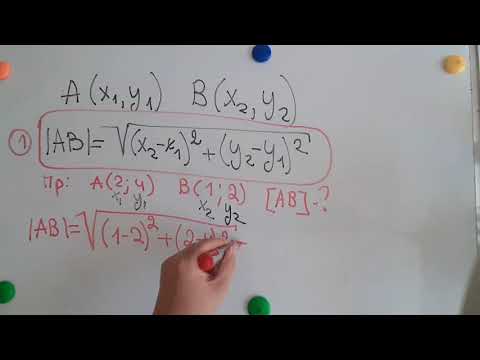
Евклидово пространство

Одной из важнейших задач геометрии является задача измерения расстояния между двумя объектами. В произвольном линейном пространстве мы пока не можем определить насколько «близки» между собой объекты. В настоящем разделе понятие расстояния между двумя векторами — элементами линейного пространства — будет вводиться посредством скалярного произведения векторов. Насколько обоснован такой порядок введения понятий:

$ mbox qquad $ скалярное произведение $ to $ длина ?

Ведь в аналитической геометрии последовательность кажется более «естественной»: скалярное произведение двух векторов $ X_ $ и $ Y_ $ определялось как произведение длин этих векторов на косинус угла между ними: $ langle X,Y rangle = |X| cdot |Y| cdot cos (widehat) $. Тем не менее, формально непротиворечива и обратная схема: если допустить, что скалярное произведение любых двух векторов может быть как-то вычислено (например, в $ mathbb R^ $ по формуле $ langle X,Y rangle = x_1y_1+x_2y_2+x_3y_3 $ при заданных прямоугольных координатах $ (x_1,x_2,x_3) $ и $ (y_1,y_2,y_3) $ векторов $ X_ $ и $ Y_ $), то и длину векторов и угол между ними можно выразить через подходящие скалярные произведения: $$ |X|=sqrt,qquad widehat=arccos frac<sqrt> .$$

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Определения

Вещественное линейное пространство $ mathbb E_ $ называется евклидовым 1) , если в этом пространстве определена функция, ставящая в соответствие паре векторов $ subset mathbb E $ вещественное число, называемое скалярным произведением векторов 2) $ X_ $ и $ Y_ $, и обозначаемое $ langle X,Y rangle_ $ или $ (X,Y)_ $; при этом фцнкция подчиняется аксиомам:

1. $ langle X,Y rangle= langle Y,X rangle $ для $ subset mathbb E $;
2. $ langle X_1+X_2,Y rangle = langle X_1,Y rangle + langle X_2,Y rangle $ для $ subset mathbb E $;
3. $ langle lambda, X,Yrangle=lambda, langle X,Yrangle $ для $ subset mathbb E, lambda in mathbb R $;
4. $ langle X,X rangle>0 $ для $ forall Xne mathbb O $, $ langle mathbb O,mathbb O rangle =0 $.

Из аксиом 1 и 2 вытекает свойство линейности скалярного произведения и по второму вектору:

2′. $ langle X,Y_1+Y_2 rangle = langle X,Y_1 rangle + langle X,Y_2 rangle $ для $ subset mathbb E $.

Пример 1. Пространство $ mathbb R_^ $, рассматриваемое как пространство вещественных векторов-столбцов. Для векторов

$$ X=left[begin x_1 \ vdots \ x_n end right] quad mbox quad Y=left[begin y_1 \ vdots \ y_n end right] $$ их скалярное произведение определим обобщением привычной из геометрии формулы $$ langle X,Y rangle = sum_^n x_jy_j = X^Y ; $$ в последней формуле $ ^ $ означает транспонирование. Будем называть это скалярное произведение стандартным. Легко проверить выполнимость аксиом 1 — 4 .

Однако стандартное определение скалярного произведения вовсе не является единственно допустимым; формально скалярное произведение можно ввести и другим способом. Рассмотрим (пока произвольную) вещественную квадратную матрицу $ A_ $ порядка $ n_ $ и положим $$ begin langle X,Y rangle = X^ A Y & = & a_x_1y_1+a_x_1y_2+ dots + a_x_1y_n &+ \ &+&a_x_2y_1+a_x_2y_2+ dots + a_x_2y_n &+ \ &+& dots &+ \ &+&a_x_ny_1+a_x_ny_2+ dots + a_x_ny_n & . end $$ (Здесь векторы $ X_ $ и $ Y_ $ из $ mathbb R_^ $ снова рассматриваются как столбцы.) Если матрица $ A_ $ является положительно определенной, то все аксиомы скалярного произведения будут удовлетворены.

Зачем нужна такая возможность в неоднозначности определения скалярного произведения в одном и том же пространстве? — Ответ на этот вопрос откладывается до следующего пункта. А пока приведу одно замечание 3) .

Пример 2. Пространство $ mathbb P_ $ полиномов одной переменной степеней $ le n_ $ с вещественными коэффициентами. Скалярное произведение полиномов

$$ p(x)=a_x^n+a_1x^+dots + a_n quad mbox quad q(x)=b_x^n+b_1x^+dots + b_n $$ введем формулой $$ langle p(x), q(x) rangle = sum_^n a_j b_j. $$ Легко проверить справедливость всех аксиом.

В том же пространстве $ mathbb P_ $ можно ли определить скалярное произведение формулой

$$ langle p(x),q(x) rangle = sum_^m p(x_k) q(x_k) quad npu _^m subset mathbb R ? $$

Пример 3. Линейное пространство $ mathbb R^ $ вещественных квадратных матриц порядка $ n_ $. Скалярное произведение введем формулой

Вторая интерпретация формулы связана с операцией $ operatorname $ нахождения следа матрицы, т.е. суммы элементов ее главной диагонали: $$ langle A,B rangle = operatorname left(Acdot B^ right) , . $$ Эквивалентность последнего представления определению устанавливается непосредственной проверкой.

На основании аксиом скалярного произведения, его вычисление для произвольных векторов $ X_ $ и $ Y_ $ может быть сведено к вычислению скалярных произведений векторов произвольного базиса. В самом деле, если система $ <X_1,dots,X_> $ составляет базис пространства $ mathbb E $, то, разложив оба вектора по этому базису $$X=x_1X_1+ dots +x_nX_n quad u quad Y=y_1X_1+ dots +y_nX_n , $$ получаем: $$langle X,Y rangle=langle x_1X_1+ dots +x_nX_n , y_1X_1+ dots +y_nX_n rangle=$$ $$ = left< begin &&x_1y_1 langle X_1,X_1 rangle + x_1y_2 langle X_1,X_2 rangle + dots + x_1y_n langle X_1,X_n rangle + \ &+&x_2y_1 langle X_2,X_1 rangle + x_2y_2 langle X_2,X_2 rangle + dots + x_2y_n langle X_2,X_n rangle+ \ &+ & dots qquad + \ &+&x_ny_1 langle X_n,X_1 rangle + x_ny_2 langle X_n,X_2 rangle + dots + x_ny_n langle X_n,X_n rangle end right> = $$ $$ =(x_1,x_2,dots,x_n)left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_n rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_n rangle \ dots & & & dots \ langle X_n,X_1 rangle & langle X_n,X_2 rangle & dots & langle X_n,X_n rangle end right) left(begin y_1 \ y_2 \ vdots \ y_n endright) . $$ Итак, при изменении векторов $ X_ $ и $ Y_ $ в последней формуле изменятся лишь строка и столбец координат, а промежуточная матрица останется неизменной. Задание этой матрицы, следовательно, полностью определит скалярное произведение в $ mathbb E_ $. Фактически задание скалярного произведения в разобранном выше примере пространства $ mathbb R^ $ по формуле $ langle X,Y rangle=X^AY $ можно рассматривать именно как частный случай этого при подходящем подборе базисных векторов. Согласно рассуждениям из примера $ 1_ $, матрица $$ left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_n rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_n rangle \ dots & & & dots \ langle X_n,X_1 rangle & langle X_n,X_2 rangle & dots & langle X_n,X_n rangle end right) $$ должна обладать некоторыми принципиальными свойствами. Так оно и окажется, см. ☟ НИЖЕ.

Матрицей Грама системы векторов 4) $ <X_1,dots,X_> $ называется квадратная матрица $$ G(X_1,dots,X_m)=left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right) = left[ (X_j,X_k) right]_^m . $$ Ее определитель называется определителем Грама 5) (или грамианом) системы векторов $ <X_1,dots,X_> $: $$ (X_1,dots,X_m)=left| begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right| = det left[ langle X_j,X_k rangle right]_^m . $$

С помощью матрицы Грама формула скалярного произведения записывается в виде $$ langle X,Y rangle =[x_1,dots,x_n] G(X_1,dots,X_n) left[ begin y_1 \ vdots \ y_n end right] . $$

Пример 4. В пространстве $ mathbb R^ $ столбцов из $ n_ $ элементов при стандартном способе задания скалярного произведения

$$ langle X,Y rangle = sum_^n x_jy_j quad npu quad X=[x_1,dots,x_n]<^>, Y=[y_1,dots,y_n]<^> $$ матрицу Грама системы векторов $ <X_j=[x_,x_,dots,x_]^ >_^m $ можно представить в виде произведения матриц $$ G(X_1,dots,X_)=left( begin x_ & x_ & dots & x_ \ x_ & x_ & dots & x_ \ dots & & & dots \ x_ & x_ & dots & x_ end right) left( begin x_ & x_ & dots & x_ \ x_ & x_ & dots & x_ \ vdots & & & vdots \ x_ & x_ & dots & x_ end right) . $$ Произведение имеет вид $ Mcdot M^ $ и, согласно теореме Бине-Коши, определитель этого произведения равен $ 0_ $ при $ m>n_ $ и неотрицателен при $ m le n $. НИЖЕ будет установлено, что обнаруженные свойства определителя Грама являются универсальными: они выполняются в произвольном евклидовом пространстве. См. также, «обращение» этого результата — задача 4 ☞ ЗДЕСЬ.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Свойства

Теорема. Имеет место неравенство Коши–Буняковского:

$$ langle X,Y rangle ^2 le langle X,X rangle langle Y,Y rangle quad npu forall subset mathbb E . $$

Доказательство для случая $ mathbb R^_ $ приведено ☞ ЗДЕСЬ. Для доказательства общего случая используем одну вспомогательную конструкцию. Из аксиомы 4 следует, что для $ forall lambda in mathbb R $ будет выполнено $ langle lambda, X — Y,, lambda, X — Y rangle ge 0 $. Имеем: $$ 0 le langle lambda, X — Y,, lambda, X — Y rangle le lambda^2 langle X,X rangle — 2,lambda langle X,Y rangle +(Y,Y) . $$ Квадратное относительно $ lambda_ $ неравенство будет выполнено при всех вещественных значениях этого параметра тогда и только тогда, когда дискриминант квадратного трехчлена будет отрицателен: $$ mathcal D=langle X,Y rangle^2 — langle X,X rangle langle Y,Y rangle le 0 . $$ ♦

С помощью скалярного произведения, введенного в предыдущем пункте, можно доказать справедливость интегральной формы неравенства:

$$ left( int_a^b p(t)q(t) d,t right)^2 le int_a^b p^2(t) d,t cdot int_a^b q^2(t) d,t $$ для произвольных полиномов 6) $

subset mathbb R [x] $.

Длиною вектора $ X_ $ в евклидовом пространстве $ mathbb E_ $ называется число $$ |X| = sqrt ; $$ здесь квадратный корень понимается как корень арифметический: $ |X| ge 0 $. Расстоянием между векторами $ X_ $ и $ Y_ $ называется число $ |X-Y| $.

В $ mathbb R^_ $ при скалярном произведении, заданном стандартным способом формулой

$$ langle X,Y rangle = sum_^n x_jy_j quad npu quad X=[x_1,dots,x_n]<^>, Y=[y_1,dots,y_n]<^> , $$ длина вектора $ X_ $ определяется естественным (с точки зрения геометрии) способом: $ |X|=sqrt $.

Теорема. Имеет место неравенство треугольника

$$ |X+Y| le |X|+|Y| quad npu forall subset mathbb E . $$

Доказательство. На основании неравенства Коши-Буняковского, имеем: $$ 0 le langle X+Y,, X+Y rangle=langle X,X rangle+2langle X,Y rangle+langle Y,Y rangle le |X|^2+2, |X| cdot |Y| +|Y|^2=left(|X|+|Y| right)^2 . $$ ♦

Углом между векторами $ X_ $ и $ Y_ $ называется угол $$varphi = widehat = arccos frac .$$ Ввиду неравенства Коши-Буняковского это определение непротиворечиво: дробь под знаком арккосинуса не превосходит 1 по абсолютной величине. Векторы $ X_ $ и $ Y_ $ называются ортогональными: $ X bot Y $ если угол между ними равен $ pi/2 $, или, что то же, $ langle X,Y rangle=0 $.

Введенное таким определением понятие является естественным обобщением понятия угла на плоскости и в трехмерном пространстве. Хотя в пространствах размерностей больших $ 3_ $ человеческие мозги думать не приучены, тем не менее, абстракция находит практическое применение в задаче информационного поиска.

Пусть задача заключается в сравнении двух текстовых документов «на похожесть». Имеются некоторые наборы ключевых слов, описывающих каждый из этих документов. Составим объединение этих наборов, упорядочим получившийся набор (пронумеруем слова), посчитаем частоты вхождений каждого из слов в каждый из документов. Получим два вектора: $$ X_1=(f_,f_,dots), X_2=(f_,f_,dots) , $$ описывающие каждый из документов. Здесь $ f_ in $ — количество вхождений $ k_ $-го слова в $ j_ $-й документ. Для оценки близости векторов, на первый взгляд, кажется естественным вычислить расстояние между ними стандартным способом: $$ |X_1-X_2| = sqrt < sum_(f_-f_)^2> . $$ Однако, по здравому размышлению, понимаем, что при таком способе, документы различные по объему (общему количеству слов) будут слишком сильно отличаться друг от друга, при том, что могут оказаться близкими по сути (как будет отличаться большая статья от собственного реферата). Поэтому имеет смысл усреднить частоты в обоих текстах, т.е. рассматривать расстояние между векторами $ X_1/|X_1| $ и $ X_2/|X_2| $ единичной длины: $$ left|frac-fracright| = sqrt<2left( 1- frac right)> ; $$ скалярное произведение под знаком корня вычисляется стандартным способом: $ langle X_1,X_2 rangle=sum_ f_f_ $. Отсюда и возникает понятие косинусного расстояния: величина $$ frac $$ неотрицательна (поскольку компоненты векторов $ X_1,X_2 $ неотрицательны), и чем ближе она к $ 1_ $ тем меньше расстояние между между нормированными векторами. Эта величина называется также похожестью или cходством 8) векторов (документов) $ X_ $ и $ X_ $.

Теорема [Пифагор]. Если $ X bot Y $, то $ |X+Y|^2=|X|^2+|Y|^2 $.

Если векторы $ X_1,dots,X_k $ попарно взаимно ортогональны, то

Пример. Найти расстояние между полиномами

$$p(x)=x^-1/2,x^-1/2,x^+5,x^-5,x^+5,x^2+1 quad u quad q(x)=5,x^2+1 $$ если скалярное произведение задается формулой а) $ displaystyle langle p(x), q(x) rangle = sum_^ a_j b_j $ ; б) $ displaystyle langle p(x), q(x) rangle = int_^1 p(t)q(t) d, t $.

Решение. Для случая а) нам достаточно просто вычислить сумму квадратов коэффициентов разности $ p(x)-q(x) $: расстояние равно $ sqrt $.

Для случая б) нам придется иметь дело с интегралом $$ int_^1 left(p(t)-q(t) right)^2 d, t = int_^1 left(t^-1/2,t^-1/2,t^+5,t^-5,t^ right)^2 d, t , $$ который, несмотря на свой громоздкий вид, может быть вычислен элементарными приемами математического анализа. В этом случае расстояние будет равно $ sqrt $.

Ответ. а) $ approx 7.176 $ ; б) $ approx 0.076 $.

Теперь прокомментируем последний пример. В разделе, посвященном полиному одной переменной, имеется теорема о непрерывной зависимости корней полинома от его коэффициентов. Смысл этого результата в следующем: если коэффициенты полиномов

$$f(x)=x^n+a_1x^+dots+a_n quad u quad (x)=x^n+_1x^+dots+_n$$ из $ mathbb C[x] $ близки, то и корни этих полиномов (при соответствующей нумерации) будут близки на комплексной плоскости. В этой теореме мера близости полиномов оценивается по формуле $$ sqrt[n]<sum_^n|a_k-_k| gamma^ > quad npu quad gamma = max_<jin > left( sqrt[j] , sqrt[j]<|_j|> right) , $$ которая, хоть и не совпадает с формулой $$ sqrt<sum_^n left(a_k-_k right)^2> , $$ определяющей расстояние в пространстве полиномов, но идейно ей близка. Вычисленное в предыдущем примере расстояние между полиномами $ p_(x) $ и $ q_(x) $ по формуле а) оказывается достаточно большим в том смысле, что если для полинома $ p_(x) $ искать полином, имеющий почти такое же расположение корней на $ mathbb C_ $, то полином $ q_(x) $ окажется неподходящим кандидатом. 9)

Другое дело, если ставится задача приближения полинома $ p_(x) $ только на интервале $ [-1,1] $ — тогда полином $ q_(x) $ может оказаться вполне полезным. Выясним сначала природу интеграла, возникшего при решении. Пусть сначала $ p_(x) $ и $ q_(x) $ — произвольные, но (для простоты рассуждений) неотрицательные на интервале $ [a_,b] $ полиномы. Геометрический смысл интеграла $ int_a^b p(t) d, t $ — площадь криволинейной трапеции на плоскости $ (x_,y) $, ограниченной прямыми $ x=a_,,x=b,,y=0 $ и графиком $ y=p(x) $. Следовательно, геометрический смысл интеграла $$ int_a^b left| p(t)-q(t) right| d, t $$ — площадь фигуры, ограниченной прямыми $ x=a,,x=b_ $ и графиками $ y=p(x), y=q(x) $ 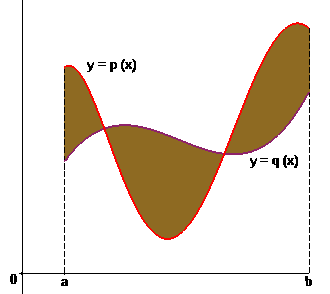(заштрихована коричневым на рисунке). Чем меньше эта площадь, тем «теснее» друг к другу на отрезке $ [a_,b] $ расположены графики $ y=p(x) $ и $ y=q(x) $. Величина $$ sqrt , $$ вообще говоря, не совпадает с предыдущей, но смысл ее тот же: она позволяет оценивать близость графиков на всем отрезке $ [a_,b] $. Ответ в примере для варианта б) позволяет заключить, что на отрезке $ [-1,1] $ полином $ p_(x) $ неплохо приближается своими младшими одночленами, т.е. на указанном отрезке график $ y=p(x) $ не должен слишком сильно отличаться от параболы $ y=5,x^2+1 $.

Подводя итог приведенным рассуждениям, можно только повторить: метод, выбираемый для оценки близости между объектами, может зависеть от поставленной задачи. Микроскоп не пригоден для наблюдения за большими объектами, а телескоп — за малыми.

Следующий результат также имеет название, взятое из планиметрии, где он формулируется так: сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин его сторон.

Теорема. В евклидовом пространстве имеет место равенство параллелограмма

$$ |X+Y|^2+|X-Y|^2 =2(|X|^2+|Y|^2) quad npu forall subset mathbb E . $$

Видео:А.5.9 Евклидово расстояние между точками (длина отрезка)Скачать

Ортогонализация

Пусть $ dim mathbb E=n $ и векторы $ $ составляют базис $ mathbb E_ $. Этот базис называется ортогональным если векторы попарно ортогональны: $ X_jbot X_k $; базис называется нормированным если каждый его вектор имеет единичную длину: $ |X_j|=1 $; базис называется ортонормированным если он ортогонален и нормирован, т.е. $$langle X_j,X_k rangle=delta_ ,quad npu quad subset .$$ Здесь $ delta_^ $ — символ Кронекера.

Ортогональный базис будем обозначать $ _1,dots, _n $.

Чему равно расстояние между двумя векторами ортонормированного базиса?

В пространстве $ mathbb R_^ $ стандартным ортогональным базисом является базис, состоящий из векторов $$ _j = big[underbrace_,0,dots,0big]^ quad npu quad j in . $$ Существование же ортогонального базиса в произвольном евклидовом пространстве еще требует доказательства. Предварительно установим следующий результат.

Теорема. Если ненулевые векторы $ X_1,dots, X_ $ попарно ортогональны, то они линейно независимы.

Доказательство. В самом деле, если $$ lambda_1 X_1 + dots + lambda_n X_n = mathbb O , $$ то, домножив это равенство скалярно на $ X_ $, получим $$ lambda_1 langle X_1,X_1 rangle + dots + lambda_n langle X_1,X_n rangle = 0 . $$ Поскольку $ langle X_1,X_j rangle=0 $ для $ jin $, то $ lambda_1 langle X_1,X_1 rangle=0 $, откуда $ lambda_1=0 $. Аналогично показывается, что и все остальные $ lambda_j $ равны 0. ♦

Задача. Пусть имеется произвольная система $ $ линейно независимых векторов. Требуется построить систему ортогональных векторов $ left<_1,dots, _k right> $ такую, чтобы линейные оболочки любых подсистем совпадали: $$ left(X_1,dots,X_m right) =left(_1,dots, _m right) quad npu quad min . $$ Иными словами, вектор $ _1 $ должен линейно зависеть от $ X_ $, вектор $ _2 $ должен линейно выражаться через $ X_1,X_2 $, $ _3 $ — через $ X_1,X_2,X_3 $ и т.д.

Алгоритм ортогонализации Грама — Шмидта 10)

В случае $ m_=1 $ возьмем $ _1=X_1 $: поскольку вектор $ X_ $ входит в линейно независимую систему , то $ _1 ne mathbb O $. Далее, будем искать $ _2 $ в виде $$_2=X_2 + alpha_ _1 $$ при пока неопределенном коэффициенте $ alpha_ $. Очевидно, что при таком выборе $ _2 $ условие $ (X_1,X_2)=(_1,_2) $ будет выполнено. Подберем $ alpha_ $ так, чтобы выполнялось $ _2 bot _1 $. $$0=langle _1,_2 rangle=langle _1,X_2 rangle+alpha_ langle _1,_1 rangle Rightarrow alpha_=-langle _1,X_2 rangle big/ langle _1,_1 rangle . $$ Таким образом, коэффициент $ alpha_ $, а вместе с ним и вектор $ _2 $ определяются единственным образом. При этом $ _2ne mathbb O $, ибо, в противном случае, векторы $ X_2 $ и $ _1=X_1 $ были бы л.з., что противоречит предположению о линейной независимости системы $ $. Продолжаем процесс далее: вектор $ _3 $ ищем в виде $$_3=X_3 + alpha_ _1 + alpha_ _2 $$ при пока неопределенных коэффициентах $ alpha_ $ и $ alpha_ $. Условие $ (X_1,X_2,X_3)=(_1,_2,_3) $ выполняется поскольку $$alpha_ _1 + alpha_ _2 in (X_1,X_2) subset (X_1,X_2,X_3) .$$ Подберем скаляры $ alpha_ $ и $ alpha_ $ так, чтобы выполнялось $ _3 bot _1 $ и $ _3 bot _2 $. Два этих условия задают систему линейных уравнений $$left< begin langle X_3,_1 rangle + alpha_ langle _1, _1 rangle + alpha_ langle _2 , _1 rangle &=0 ,\ langle X_3,_2 rangle + alpha_ langle _1, _2 rangle + alpha_ langle _2 , _2 rangle &=0 , end right. iff begin alpha_=-langle X_3,_1 rangle big/ |_1|^2 \ alpha_=-langle X_3,_2 rangle big/ |_2|^2 end $$

Процесс продолжается далее аналогично. Допустим, что векторы $ _1,dots,_ $ уже построены, они ненулевые, попарно ортогональные и $$ left(X_1,dots,X_ right)= left(_1,dots, _ right) .$$ Вектор $ _ $ ищем в виде: $$ _ =X_k+alpha_ _1 + alpha_ _2 +dots + alpha_ _ $$ при пока неопределенных коэффициентах $ alpha_,dots ,alpha_ $. Условие $ left(X_1,dots,X_,X_k right)= left(_1,dots, _,_ right) $ выполнено и, кроме того, $ _ne mathbb O $ (в противном случае $ X_k in left(_1,dots, _ right) =left(X_1,dots,X_ right) $, т.е. система $ <X_1,dots,X_,X_k > $ линейно зависима. Коэффициенты $ alpha_, dots ,alpha_ $ подбираются из условий $ _ bot _1,dots, _ bot _ $. Получающаяся система линейных уравнений имеет единственное решение $$alpha_=- langle X_k,_1 rangle big/ |_1|^2 ,dots, alpha_=-langle X_k,_ rangle big/ |_|^2 , $$ и это решение определяет единственный вектор $ _ $. ♦

Пример. Ортогонализовать систему векторов

$$ X_1=left[1,0,0,0,1 right], X_2=left[1,1,0,1,1 right], X_3=left[1,1,1,1,1 right] $$ при стандартном способе задания скалярного произведения в $ mathbb R^5 $.

Пример. Пусть в пространстве полиномов скалярное произведение задается формулой

$$ langle p(x),q(x) rangle=int_^ p(t)q(t) d, t .$$ Построить ортогональный базис этого пространства.

Решение. Искомый базис строится ортогонализацией канонического базиса $ 1,x,x^2,dots, x^n $. В результате получаем систему полиномов: $$1, x, x^2-frac, x^3-frac, x, x^4-frac, x^2+frac,dots $$ Полиномы, получающиеся из этих нормированием: $$P_0(x)=1, P_1(x)= x, P_2(x)=frac(3,x^2-1), P_3(x)= frac( 5,x^3-3, x), $$ $$ P_4(x)= frac(35,x^4-30, x^2+3),dots $$ $$ P_n(x)=frac sum_^ frac x^ $$ известны как полиномы Лежандра. Здесь $ lfloor mbox rfloor $ означает целую часть числа. Рекуррентное соотношение $$kP_(x)-(2k-1),xP_(x)+(k-1),P_(x) equiv 0, quad kge 2 ;$$ позволяет найти полином $ P_(x) $ если уже вычислены $ P_(x) $ и $ P_(x) $. ♦

В ортонормированном базисе пространства $ mathbb E_ $ матрица Грама из формулы скалярного произведения $$ langle X,Y rangle=(x_1,dots,x_n) G(X_1,dots,X_n) left( begin y_1 \ vdots \ y_n end right) $$ становится единичной и в таком базисе скалярное произведение становится стандартным : $$ langle X,Y rangle=sum_^n x_jy_j .$$

Следующая теорема устанавливает связь между двумя ортонормированными базисами в одном и том же пространстве.

Теорема. Матрица перехода от одного ортонормированного базиса к другому является ортогональной.

В пространстве $ mathbb R^_ $ матрица, составленная из столбцов произвольного ортонормированного базиса, является ортогональной.

Матричный формализм алгоритма Грама-Шмидта: QR-разложение

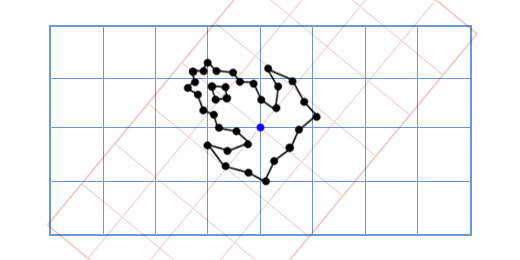
Рассмотрим пример из предыдущего пункта об ортогонализации системы векторов в $ mathbb R^5 $; только векторы будем рассматривать столбцами: $$ X_1=left[begin 1 \ 0 \ 0 \ 0 \ 1 end right], X_2=left[ begin 1 \ 1 \ 0 \ 1 \ 1 end right], X_3=left[ begin 1 \ 1 \ 1 \ 1 \ 1 end right] , . $$ Составим из них матрицу $$ A_ = left[ X_1,X_2,X_3 right] , . $$ Алгоритм Грама-Шмидта означает некоторые действия со столбцами этой матрицы, и эти действия могут быть записаны на языке матричного формализма, а именно — с помощью операции умножения этой матрицы на последовательность матриц определенного вида. В самом деле, на первом шаге алгоритма, «все остается на месте»: столбец $ _1 $ совпадает с $ X_ $, а оставшиеся столбцы мы пока не трогаем. Формально это «бездействие» можно записать с помощью умножения матрицы $ A_ $ на единичную матрицу порядка $ 3_ $. $$ Acdot E_ = left[_1,X_2,X_3 right] , . $$ Следующий шаг алгоритма уже менее тривиален: в получившейся матрице производятся действия над первыми двумя столбцами. При этом первый столбец остается неизменным, последний — тоже, а изменяется лишь второй: $$ _2 = X_2 + alpha_ _1 , . $$ Для получившейся на первом шаге матрицы, это действие эквивалентно домножению ее справа на матрицу $$ R_2 = left( begin 1 & alpha_ & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end right) , . $$ Если значение $ alpha_ $ вычисляется как указано в алгоритме: $$alpha_=- langle _1,X_2 rangle big/ langle _1,_1 rangle =- langle X_1,X_2 rangle big/ langle X_1,X_1 rangle , , $$ то получившаяся матрица $$ Acdot E_ R_2 = left[_1,_2,X_3 right] $$ имеет первые два столбца ортогональными. Следующее преобразование получившейся системы столбцов равносильно домножению получившейся матрицы справа на матрицу вида $$ R_3 = left( begin 1 & 0 & alpha_ \ 0 & 1 & alpha_ \ 0 & 0 & 1 end right) , . $$ Если значения $ alpha_ $ и $ alpha_ $ вычисляются как указано в алгоритме, то получившаяся матрица $$ Acdot E_ R_2 R_3 = left[_1,_2,_3 right] $$ имеет систему своих столбцов ортогональной. Можно произвести еще одно дополнительное домножение $$ Acdot E_ R_2 R_3 cdot left( begin 1/langle _1,_1 rangle & 0 & 0 \ 0 & 1/langle _2,_2 rangle & 0 \ & 0 & 1/ langle _3,_3 rangle end right) , , $$ превратив полученную матрицу в матрицу с ортонормированной системой столбцов.

Теперь обдумаем полученный результат. Матрицы, на которые производились домножения матрицы $ A_ $ имеют довольно специфическую форму: они — либо диагональные, либо же отличаются от единичной матрицы в одном их своих столбцов. Эти матрицы могут быть отнесены к типу матриц элементарных преобразований системы столбцов произвольной матрицы $ A_ $. Все они являются верхнетреугольными, и их произведение $ R_ $ относится к тому же типу. Обратная к верхнетреугольной также является верхнетреугольной. В результате, можно получить разложение матрицы $ A_ $ в произведение $$ A=Q_R^ , , $$ где вторая матрица в произведении является верхнетреугольной, а первая имеет свои столбцы ортонормированными.

Теорема [о QR-разложении]. Для любой вещественной матрицы $ A_^ $ ранга $ n 11) $ tilde R_ $, такие, что $$ A=Q tilde R , . $$

Пример. Для матрицы из предыдущего примера имеем:

$$ left( begin 1 & 1 & 1 \ 0 & 1 & 1 \ 0 & 0 & 1 \ 0 & 1 & 1 \ 1 & 1 & 1 end right) = $$ $$ =left( begin 1/sqrt & 0 & 0 \ 0 & 1/sqrt & 0 \ 0 & 0 & 1 \ 0 & 1/sqrt & 0 \ 1/sqrt & 0 & 0 end right) left< left( begin 1 & -1 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end right) left( begin 1 & 0 & -1 \ 0 & 1 & -1 \ 0 & 0 & 1 end right) left( begin 1/sqrt & 0 & 0 \ 0 & 1/sqrt & 0 \ 0 & 0 & 1 end right) right>^ $$ $$ = left( begin 1/sqrt & 0 & 0 \ 0 & 1/sqrt & 0 \ 0 & 0 & 1 \ 0 & 1/sqrt & 0 \ 1/sqrt & 0 & 0 end right)left( begin sqrt & sqrt & sqrt \ 0 & sqrt & sqrt \ 0 & 0 & 1 end right) , . $$ ♦

Для квадратной неособенной вещественной матрицы $ A_ $ матрица $ Q_ $ в QR-разложении будет ортогональной.

Последний результат имеет уже самостоятельное значение, не относящееся к материалам настоящего раздела. Например, его можно использовать для обращения матрицы $ A_ $. Дело в том, что ортогональная матрица обращается достаточно просто: $ Q^ = Q^ $.

Видео:Стереометрия ЕГЭ. Метод координат. Часть 5 из 5. Расстояние между прямымиСкачать

Расстояние от точки до многообразия

Задача. Найти расстояние от заданного вектора $ X_ $ до заданного множества $ mathbb Ssubset mathbb E $.

Такая постановка требует немедленного уточнения: что такое расстояние от вектора до множества? Обратясь за помощью к геометрии, мы можем ввести это понятие, основываясь на понятии расстояния между точками: например, расстояние от точки $ Xin mathbb R^2 $ до множества $ mathbb S subset mathbb R^2 $ определить как минимальное из возможных расстояний между точками $ X_ $ и $ Y_ $, где $ Yin mathbb S $. Следующий пример показывает, что наше определение оказывается ущербным.

Пример. Множество

Доказать следующие свойства операции $ perp $:

а) $ left(mathbb E_1^<^> right)^<^>=mathbb E_1 $; б) $ left(mathbb E_1 +mathbb E_2 right)^<^>=mathbb E_1^<^> cap mathbb E_2^<^> $; в) $ left(mathbb E_1 cap mathbb E_2 right)^<^>=mathbb E_1^<^>+mathbb E_2^<^> $.

Доказать, что в пространстве квадратных матриц со скалярным произведением, заданным формулой

$$ langle A,B rangle = operatorname left(Acdot B^ right) = sum_^n a_b_ , $$ подпространство кососимметричных матриц является ортогональным дополнением подпространства симметричных матриц.

Вычисление расстояния

Теорема $ 2 $ из предыдущего пункта позволяет сформулировать результат, на котором и будет основано решение задачи вычисления расстояния.

Теорема 1. Для любого вектора $ Xin mathbb E $ существует единственное представление его в виде $$ X=X^<^>+X^<^> quad npu X^<^>in mathbb E_1, X^<^> in mathbb E_1^<^> . $$

В этом разложении вектор $ X^<^> $ называется ортогональной проекцией вектора $ X_ $ на $ mathbb E_1 $, а вектор $ X^<^> $ — ортогональной составляющей вектора $ X_ $ относительно $ mathbb E_1 $ или же перпендикуляром, опущенным из точки $ X_ $ на подпространство $ mathbb E_1 $.

Теорема 2. Длина перпендикуляра, опущенного из точки $ X_ $ на подпространство $ mathbb E_1 $ , равна расстоянию от этой точки до подпространства: $$left|X^<^>right|=min_ |X-Y| . $$

Итак, задача, поставленная в начале ☞ ПУНКТА, решается вычислением $ left|X^<^> right| $. Для нахождения последнего числа сначала найдем базис $ $ подпространства $ mathbb E_1 $. Далее, ищем $ X^<^> $, принадлежащий $ mathbb E_1 $, в виде линейной комбинации базисных векторов: $$ X^<^>=alpha_1 X_1 + dots + alpha_k X_k . $$ Для нахождения скаляров $ alpha_1,dots , alpha_k $ используем тот факт, что вектор $ X^<^>=X-X^<^> $ должен быть ортогонален $ mathbb E_1 $, а значит, ортогонален каждому $ X_j $: $$langle X-X^<^>, X_j rangle =0 iff langle X^<^>, X_j rangle=langle X,X_j rangle . $$ Получаем систему линейных уравнений: $$ left< begin alpha_1 langle X_1,X_1 rangle &+ alpha_2 langle X_1,X_2 rangle &+ dots &+ alpha_k langle X_1,X_k rangle &= langle X,X_1 rangle, \ alpha_1 langle X_2,X_1 rangle & + alpha_2 langle X_2,X_2 rangle &+ dots &+ alpha_k langle X_2,X_k rangle &= langle X,X_2 rangle, \ dots & & & & dots \ alpha_1 langle X_k,X_1 rangle & + alpha_2 langle X_k,X_2 rangle &+ dots &+ alpha_k langle X_k,X_k rangle &= langle X,X_k rangle. end right. $$ с матрицей, которая нам уже известна как матрица Грама системы векторов: $ G(X_1,dots,X_k) $. Для однозначной разрешимости относительно $ alpha_1,dots , alpha_k $ необходимо и достаточно (см. ☞ теорема Кронекера-Капелли ), чтобы определитель этой матрицы — т.е. определитель Грама $ mathfrak G(X_1,dots,X_k) $ — был отличен от нуля.

Матрица Грама обращается в единичную если векторы $ X_1,dots,X_k $ входят в состав ортонормированного базиса пространства $ mathbb E_ $. Следовательно, по крайней мере в этом частном случае, система уравнений будет иметь единственное решение. В одном из последующих ☟ ПУНКТОВ будет установлен и более общий факт: $$ mathfrak(Y_1,dots,Y_k)=0 iff quad mbox quad quad mbox $$ Этот факт позволяет нам заключить, что, поскольку векторы $ $ — базисные для подпространства $ mathbb E_1 $, то система уравнений имеет единственное решение относительно $ alpha_1,dots , alpha_k $: $$alpha_1=alpha_1^,dots , alpha_k=alpha_k^ .$$ Теперь может быть найдена проекция вектора $ X_ $ на $ mathbb E_1 $: $$ X^<^>=alpha_1^ X_1 + dots + alpha_k^ X_k , $$ а затем и составляющая: $ X^<^>=X-X^<^> $.

Пример. Найти расстояние от точки $ X=[1,1,2,2,2] $ до подпространства

$$ mathbb E_1= left< Xin mathbb R^5 left| begin x_1&-x_2&-x_3&+x_4 & &= 0, \ 2,x_1&-x_2&-x_3&+2,x_4 &-x_5 &=0 end right. right> , $$ если скалярное произведение определяется стандартно: $ langle X,Y rangle=sum_^5 x_jy_j $.

Решение. Базис $ mathbb E_1 $ составляет фундаментальная система решений системы линейных уравнений, например: $$X_1=[0,-1,1,0,0], X_2=[-1,0,0,1,0], X_3=[1,1,0,0,1] .$$ Составляем матрицу Грама этой системы векторов и выписываем систему уравнений: $$ left( begin 2 & 0 & -1 \ 0 & 2 & -1 \ -1 & -1 & 3 end right) left( begin alpha_1 \ alpha_2 \ alpha_3 end right) = left( begin 1 \ 1 \ 4 end right) Rightarrow alpha_1=frac,, alpha_2=frac,, alpha_3=frac . $$ Ортогональная проекция вектора $ X_ $ на $ mathbb E_1 $: $$ X^<^>= frac X_1 + frac X_2 + frac X_3=left[frac,, frac,, frac,, frac,, frac right] , $$ а ортогональная составляющая вектора $ X_ $ относительно $ mathbb E_1 $: $$ X^<^>=X-X^<^>= left[frac,, frac,, frac,, frac,, — frac right] quad Rightarrow left|X^<^>right| =frac<sqrt> . $$

Ответ. $ 1/sqrt $.

Альтернативный способ вычисления расстояния от точки до линейного многообразия, заданного системой линейных уравнений ☞ ЗДЕСЬ.

Расстояние от точки $ X_ $ до линейного подпространства, базисными векторами которого являются $ X_1,dots,X_k $, вычисляется по формуле: $$ d=sqrt<frac<(X_1,dots,X_k, X)><(X_1,dots,X_k)>> . $$

Доказательство ☞ ЗДЕСЬ.

Пример. В пространстве полиномов с вещественными коэффициентами степеней не выше $ 5_ $ со скалярным произведением, заданным формулой

$$langle p(x),q(x) rangle = int_^1 p(t)q(t) d,t $$ найти расстояние от полинома $ p(x)= -x^5+x^3-3,x+1 $ до линейного подпространства четных полиномов.

Решение. Базис подпространства четных полиномов состоит, например, из $ 1,x^2,x^4 $. Имеем: $$ (1,x^2,x^4)=left| begin int_^1 1 cdot 1 d,t & int_^1 1 cdot t^2 d,t & int_^1 1 cdot t^4 d,t \ int_^1 1 cdot t^2 d,t & int_^1 t^2 cdot t^2 d,t & int_^1 t^2cdot t^4 d,t \ int_^1 1 cdot t^4 d,t & int_^1 t^2 cdot t^4 d,t & int_^1 t^4 cdot t^4 d,t end right|=left| begin 2 & 2/3 & 2/5 \ 2/3 & 2/5 & 2/7 \ 2/5 & 2/7 & 2/9 end right|=frac ; $$ $$ (1,x^2,x^4,p(x))=left| begin 2 & 2/3 & 2/5 & 2 \ 2/3 & 2/5 & 2/7 & 2/3 \ 2/5 & 2/7 & 2/9 & 2/5 \ 2 & 2/3 & 2/5 & 3632/495 end right|=frac . $$ Отношение полученных определителей даст квадрат расстояния: $$ d^2=2642/495 . $$ К этому же ответу можно было прийти и быстрее если заметить, что при заданном скалярном произведении любой четный полином ортогонален любому нечетному полиному. Следовательно для выделения у $ p(x) $ ортогональной составляющей относительно подпространства четных полиномов достаточно оставить в его каноническом виде только нечетные одночлены. Расстояние равно норме полинома $ p(x)-1 $. ♦

Подводя итог: определители Грама полностью решают задачу о вычислении расстояния от точки до линейного подпространства в любом евклидовом пространстве; этот результат легко обобщается на произвольное линейное многообразие.

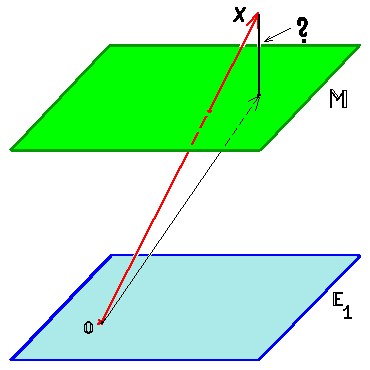
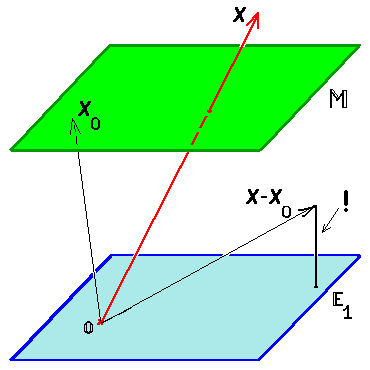
Теорема 3. Расстояние от точки $ X_ $ до линейного многообразия $ mathbb M=X_0+mathbb E_1 $ равно длине ортогональной составляющей вектора $ X-X_0 $ относительно подпространства $ mathbb E_1 $.

Доказательство. Геометрический смысл понятен из рисунков, иллюстрирующих решение проблемы в $ mathbb R^ $: надо свести задачу к случаю из предыдущей теоремы с помощью сдвига всей конструкции на вектор $ (-X_0) $.

Формальности: $$ min_ |X-Y| =min_ |X-(X_0+Z)|= min_ |(X-X_0)-Z)| . $$ Последняя величина — это расстояние от точки $ X-X_0 $ до $ mathbb E_1 $ ; согласно теореме $ 2 $ оно равно длине ортогональной составляющей вектора $ X-X_0 $ относительно $ mathbb E_1 $. ♦

Расстояние от точки $ X_ $ до линейного многообразия, заданного параметрически

Вычисление расстояния между линейными многообразиями (и некоторыми другими объектами, заданными алгебраическими уравнениями) ☞ ЗДЕСЬ.

Угол между вектором и линейным многообразием

Углом между вектором $ Xin mathbb E $ и линейным подпространством $ mathbb E_1 subset mathbb E $ назовем число — точную нижнюю грань множества углов между $ X_ $ и всевозможными векторами $ Y in mathbb E_1 $. Углом между вектором $ Xin mathbb E $ и линейным многообразием $ mathbb M=X_0+mathbb E_1 $ называется угол между $ X_ $ и $ mathbb E_1 $.

Теорема. Угол между вектором $ Xin mathbb E $ и линейным подпространством $ mathbb E_1 subset mathbb E $ равен углу между этим вектором и его ортогональной проекцией $ X^<^> $ на $ mathbb E_1 $.

Эта теорема сводит задачу к решенной в предыдущих пунктах задаче вычисления расстояния от вектора до подпространства, только теперь интерес смещается от ортогональной составляющей вектора к его ортогональной проекции.

Пример. Определить угол между вектором $ X_0=[1,0,3,0] $ и линейной оболочкой

Решение. Воспользуемся результатом, приведенным ☞ ЗДЕСЬ (для правильной стыковки рассматриваем все векторы как столбцы): $$ X_=L(L^ L_)^ L^ X_0 , . $$ Здесь $$ L=left(begin 5 & 1 & 2 \ 3 & 1 & -1 \ 4 & 4 & 1 \ -3 & 5 & 2 end right), qquad L^ L = left(begin 59 & 9 & 5 \ 9 & 43 & 15 \ 5 & 15 & 10 end right), $$ $$ (L^ L )^ = left(begin 41/2312 & -3/2312 & -2/289\ -3/2312 & 113/2312 & -21/289\ -2/289 & -21/289 & 307/1445 end right) $$ $$ L(L^ L_)^ L^= left(begin 9/10 & -1/5 & 1/5 & -1/10 \ -1/5 & 3/5 & 2/5 & -1/5 \ 1/5 & 2/5 & 3/5 & 1/5\ -1/10 & -1/5 & 1/5 & 9/10 end right), quad X_= left(begin 3/2 \ 1 \ 2 \ 1/2 end right) , . $$ $$ widehat<X_0,X_>=arccos frac <langle X_0,X_rangle ><sqrt< langle X_0,X_0rangle langle X_,X_ rangle>>= arccos frac<sqrt>= frac , . $$ ♦

Видео:Видеоурок "Расстояние между прямыми в пространстве"Скачать

Свойства матрицы Грама

Теорема. $ (X_,dots,X_m)=0 $ тогда и только тогда, когда система векторов $ <X_,dots,X_m > $ линейно зависима.

Доказательство. Если система векторов $ <X_,dots,X_m> $ линейно зависима, то имеет место равенство $$alpha_1 X_1+alpha_2 X_2+dots+alpha_ X_=mathbb O$$ при некотором нетривиальном наборе скаляров $ alpha_1=alpha_1^,dots,alpha_m=alpha_m^ $. Домножим это соотношение (скалярно) на векторы $ X_1,X_2,dots,X_m $, получим систему уравнений, которую перепишем в матричном виде: $$ left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right) left( begin alpha_1 \ alpha_2 \ vdots \ alpha_m end right)= left( begin 0 \ 0 \ vdots \ 0 end right) . $$ Если рассмотреть эту систему относительно переменных $ alpha_,dots,alpha_m $, то она оказывается однородной и, по предположенному, будет иметь нетривиальное решение $ alpha_1=alpha_1^,dots,alpha_m=alpha_m^ $ . Следовательно (см. ☞ ТЕОРЕМА КРОНЕКЕРА-КАПЕЛЛИ ) ее определитель равен нулю: $ (X_,dots,X_m)=0 $.

Обратно, если определитель Грама равен нулю, то предыдущая система имеет нетривиальное решение относительно $ alpha_,dots,alpha_m $. Пусть $ alpha_1=alpha_1^,dots,alpha_m=alpha_m^ $ — какое-то из этих решений. Составим вектор $$X^= alpha_1^ X_1+alpha_2^ X_2+dots+alpha_^ X_ $$ и вычислим скалярное произведение его на самого себя: $$ langle X^,X^ rangle = $$ $$ = (alpha_1^ ,alpha_2^ ,dots,alpha_m^ ) underbrace<left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right) left(begin alpha_1^ \ alpha_2^ \ vdots \ alpha_m^ endright)>_<=mathbb O_>=0 . $$ Таким образом длина вектора $ X^ $ равна нулю, и, следовательно, по аксиоме 4 , сам вектор $ X^ $ — нулевой. Но тогда система векторов $ <X_,dots,X_m> $ линейно зависима. ♦

Ранг матрицы Грама совпадает с рангом системы порождающих ее векторов:

Если какой-то главный минор матрицы Грама обращается в нуль, то и все главные миноры бóльших порядков обращаются в нуль.

Теорема. $ (X_,dots,X_m) ge 0 $ для любого набора векторов $ <X_,dots,X_m > $.

Доказательство ☞ ЗДЕСЬ

Матрица Грама линейно независимой системы векторов является положительно определенной. Матрица Грама произвольной системы векторов является положительно полуопределенной.

Дальнейшие свойства матрицы и определителя Грама ☞ ЗДЕСЬ

Видео:✓ Расстояние между скрещивающимися прямыми | ЕГЭ-2018. Задание 13. Математика | Борис ТрушинСкачать

Задачи

Видео:Длина отрезкаСкачать

Источник

Материалы этого раздела составлены на основе книги

Шилов Г.Е. Математический анализ. Конечномерные линейные пространства. М.Наука.1969

Видео:Расстояние между точками. Геометрия 9 класс.Скачать

Линейная алгебра для разработчиков игр

Эта статья является переводом цикла из четырёх статей «Linear algebra for game developers», написанных David Rosen и посвящённых линейной алгебре и её применению в разработке игр. С оригинальными статьями можно ознакомиться тут: часть 1, часть 2, часть 3 и часть 4. Я не стал публиковать переводы отдельными топиками, а объединил все статьи в одну. Думаю, что так будет удобнее воспринимать материал и работать с ним. Итак приступим.

Зачем нам линейная алгебра?

Одним из направлений в линейной алгебре является изучение векторов. Если в вашей игре применяется позиционирование экранных кнопок, работа с камерой и её направлением, скоростями объектов, то вам придётся иметь дело с векторами. Чем лучше вы понимаете линейную алгебру, тем больший контроль вы получаете над поведением векторов и, следовательно, над вашей игрой.

Что такое вектор?

В играх вектора используются для хранения местоположений, направлений и скоростей. Ниже приведён пример двухмерного вектора: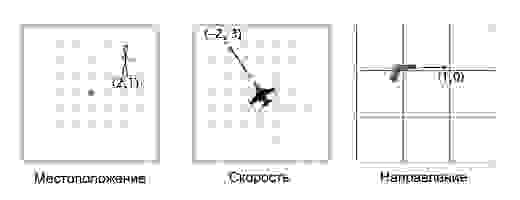

Вектор местоположения (также называемый «радиус-вектором») показывает, что человек стоит в двух метрах восточнее и в одном метре к северу от исходной точки. Вектор скорости показывает, что за единицу времени самолёт перемещается на три километра вверх и на два — влево. Вектор направления говорит нам о том, что пистолет направлен вправо.

Как вы можете заметить, вектор сам по себе всего лишь набор цифр, который обретает тот или иной смысл в зависимости от контекста. К примеру, вектор (1, 0) может быть как направлением для оружия, как показано на картинке, так и координатами строения в одну милю к востоку от вашей текущей позиции. Или скоростью улитки, которая двигается вправо со скоростью в 1 милю в час (прим. переводчика: довольно быстро для улитки, 44 сантиметра в секунду).

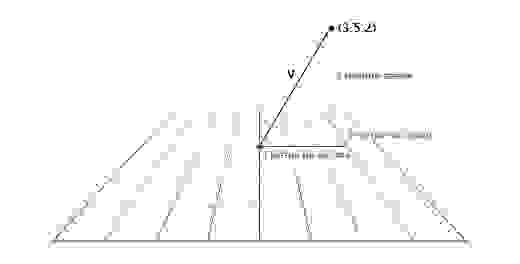
Важно отслеживать единицы измерения. Допустим у нас есть вектор V (3,5,2). Это мало что говорит нам. Три чего, пять чего? В нашей игре Overgrowth расстояния указываются в метрах, а скорости в метрах в секунду. Первое число в этом векторе — это направление на восток, второе — направление вверх, третье — направление на север. Отрицательные числа обозначают противоположные направления, на запад, вниз и на юг. Местоположение, определяемое вектором V (3,5,2), находится в трёх метрах к востоку, в пяти метрах вверху и в двух метрах к северу, как показано на картинке ниже.

Итак, мы изучили основы работы с векторами. Теперь узнаем как вектора использовать.

Сложение векторов

Чтобы сложить вектора, нам надо просто сложить каждую их составляющую друг с другом. Например:

(0, 1, 4) + (3, -2, 5) = (0+3, 1-2, 4+5) = (3, -1, 9)

Зачем нам нужно складывать вектора? Наиболее часто сложение векторов в играх применяется для физического интегрирования. Любой физический объект будет иметь вектора для местоположения, скорости и ускорения. Для каждого кадра (обычно это одна шестидесятая часть секунды), мы должны интегрировать два вектора: добавить скорость к местоположению и ускорение к скорости.

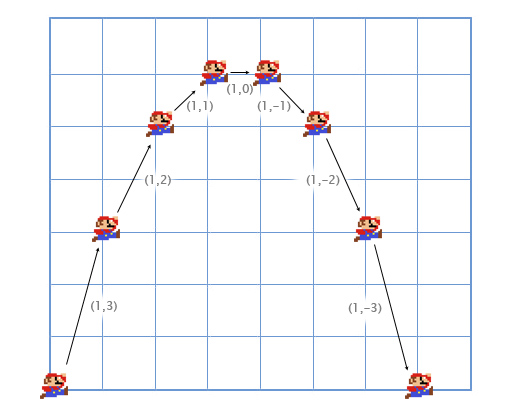
Давайте рассмотрим пример с прыжками Марио. Он начинает с позиции (0, 0). В момент начала прыжка его скорость (1, 3), он быстро двигается вверх и вправо. Его ускорение равно (0, -1), так как гравитация тянет его вниз. На картинке показано, как выглядит его прыжок, разбитый на семь кадров. Чёрным текстом показана его скорость в каждом фрейме.

Давайте рассмотрим первые кадры поподробнее, чтобы понять как всё происходит.

Для первого кадра, мы добавляем скорость Марио (1, 3) к его местоположению (0, 0) и получаем его новые координаты (1, 3). Затем мы складываем ускорение (0, -1) с его скоростью (1, 3) и получаем новое значение скорости Марио (1, 2).

Делаем то-же самое для второго кадра. Добавляем скорость (1, 2) к местоположению (1, 3) и получаем координаты (2, 5). Затем добавляем ускорение (0, -1) к его скорости (1, 2) и получаем новую скорость (1, 1).

Обычно игрок контролирует ускорение игрового персонажа с помощью клавиатуры или геймпада, а игра, в свою очередь, рассчитывает новые значения для скоростей и местоположения, используя физическое сложение (через сложение векторов). Это та-же задача, которая решается в интегральном исчислении, просто мы его сильно упрощаем для нашей игры. Я заметил, что мне намного проще внимательно слушать лекции по интегральному исчислению, думая о практическом его применении, которое мы только что описали.

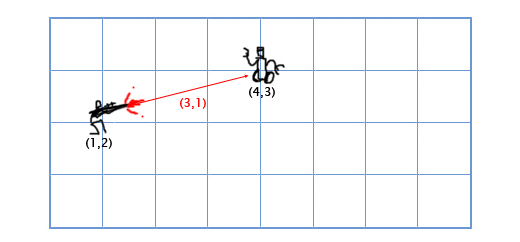
Вычитание векторов

Вычитание рассчитывается по тому-же принципу что и сложение — вычитаем соответствующие компоненты векторов. Вычитание векторов удобно для получения вектора, который показывает из одного местоположения на другое. Например, пусть игрок находится по координатам (1, 2) с лазерным ружьём, а вражеский робот находится по координатам (4, 3). Чтобы определить вектор движения лазерного луча, который поразит робота, нам надо вычесть местоположение игрока из местоположения робота. Получаем:

(4, 3) — (1, 2) = (4-1, 3-2) = (3, 1).

Умножение вектора на скаляр

Когда мы говорим о векторах, мы называем отдельные числа скалярами. Например (3, 4) — вектор, а 5 — это скаляр. В играх, часто бывает нужно умножить вектор на число (скаляр). Например, моделируя простое сопротивление воздуха путём умножения скорости игрока на 0.9 в каждом кадре. Чтобы сделать это, нам надо умножить каждый компонент вектора на скаляр. Если скорость игрока (10, 20), то новая скорость будет:

0.9*(10, 20) = (0.9 * 10, 0.9 * 20) = (9, 18).

Длина вектора

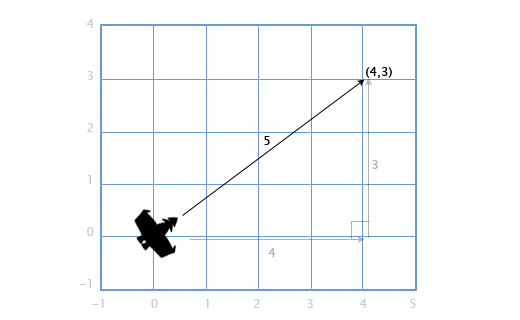
Если у нас есть корабль с вектором скорости V (4, 3), нам также понадобится узнать как быстро он двигается, чтобы посчитать потребность в экранном пространстве или сколько потребуется топлива. Чтобы сделать это, нам понадобится найти длину (модуль) вектора V. Длина вектора обозначается вертикальными линиями, в нашем случае длина вектора V будет обозначаться как |V|.

Мы можем представить V как прямоугольный треугольник со сторонами 4 и 3 и, применяя теорему Пифагора, получить гипотенузу из выражения: x 2 + y 2 = h 2

В нашем случае — длину вектора H с компонентами (x, y) мы получаем из квадратного корня: sqrt(x 2 + y 2 ).

Итак, скорость нашего корабля равна:

|V| = sqrt(4 2 + 3 2 ) = sqrt(25) = 5

Этот подход используется и для трёхмерных векторов. Длина вектора с компонентами (x, y, z) рассчитывается как sqrt(x 2 + y 2 + z 2 )

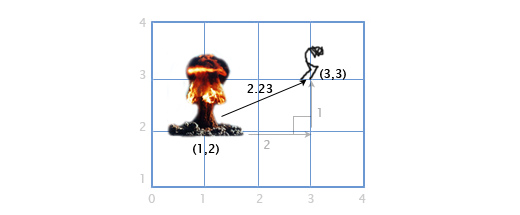
Расстояние

Если игрок P находится в точке (3, 3), а взрыв произошёл в точке E по координатам (1, 2), нам надо определить расстояние между игроком и взрывом, чтобы рассчитать степень ущерба, нанесённого игроку. Это легко сделать, комбинируя две вышеописанных операции: вычитание векторов и их длину.
Мы вычитаем P — E, чтобы получить вектор между ними. А затем определяем длину этого вектора, что и даёт нам искомое расстояние. Порядок следования операндов тут не имеет значения, |E — P| даст тот-же самый результат.

Расстояние = |P — E| = |(3, 3) — (1, 2)| = |(2, 1)| = sqrt(2 2 +1 2 ) = sqrt(5) = 2.23

Нормализация

Когда мы имеем дело с направлениями (в отличие от местоположений и скоростей), важно, чтобы вектор направления имел длину, равную единице. Это сильно упрощает нам жизнь. Например, допустим орудие развёрнуто в направлении (1, 0) и выстреливает снаряд со скоростью 20 метров в секунду. Каков в данном случае вектор скорости для выпущенного снаряда?

Так как вектор направления имеет длину равную единице, мы умножаем направление на скорость снаряда и получаем вектор скорости (20, 0). Если-же вектор направления имеет отличную от единицы длину, мы не сможем сделать этого. Снаряд будет либо слишком быстрым, либо слишком медленным.

Вектор с длиной равной единице называется «нормализованным». Как сделать вектор нормализованным? Довольно просто. Мы делим каждый компонент вектора на его длину. Если, к примеру, мы хотим нормализовать вектор V с компонентами (3, 4), мы просто делим каждый компонент на его длину, то есть на 5, и получаем (3/5, 4/5). Теперь, с помощью теоремы Пифагора, мы убедимся в том, что его длина равна единице:

(3/5) 2 + (4/5) 2 = 9/25 + 16/25 = 25/25 = 1

Скалярное произведение векторов

Что такое скалярное произведение (записывается как •)? Чтобы рассчитать скалярное произведение двух векторов, мы должны умножить их компоненты, а затем сложить полученные результаты вместе

(a1, a2) • (b1, b2) = a1b1 + a2b2

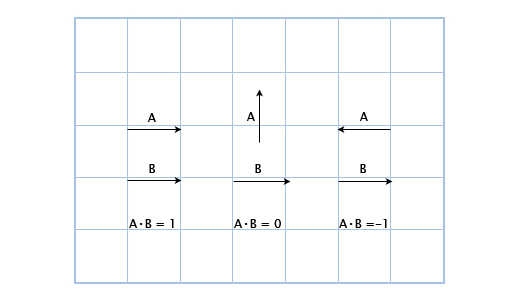
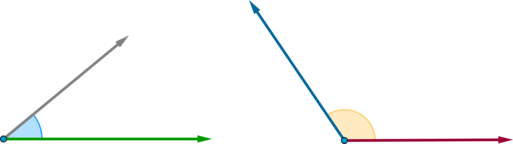
Например: (3, 2) • (1, 4) = 3*1 + 2*4 = 11. На первый взгляд это кажется бесполезным, но посмотрим внимательнее на это:

Здесь мы можем увидеть, что если вектора указывают в одном направлении, то их скалярное произведение больше нуля. Когда они перпендикулярны друг другу, то скалярное произведение равно нулю. И когда они указывают в противоположных направлениях, их скалярное произведение меньше нуля.
В основном, с помощью скалярного произведения векторов можно рассчитать, сколько их указывает в одном направлении. И хоть это лишь малая часть возможностей скалярного произведения, но уже очень для нас полезная.

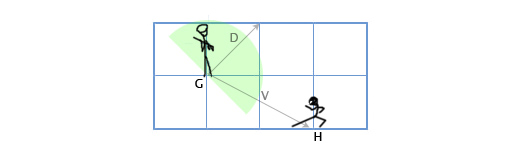
Допустим у нас есть стражник, расположенный в G(1, 3) смотрящий в направлении D(1,1), с углом обзора 180 градусов. Главный герой игры подсматривает за ним с позиции H(3, 2). Как определить, находится-ли главный герой в поле зрения стражника или нет? Сделаем это путём скалярного произведения векторов D и V (вектора, направленного от стражника к главному герою). Мы получим следующее:

V = H — G = (3, 2) — (1, 3) = (3-1, 2-3) = (2, -1)
D•V = (1, 1) • (2, -1) = 1*2 + 1*-1 = 2-1 = 1

Так как единица больше нуля, то главный герой находится в поле зрения стражника.

Мы уже знаем, что скалярное произведение имеет отношение к определению направления векторов. А каково его более точное определение? Математическое выражение скалярного произведения векторов выглядит так:

Где Θ (произносится как «theta») — угол между векторами A и B.

Это позволяет нам найти Θ (угол) с помощью выражения:

Как я говорил ранее, нормализация векторов упрощает нашу жизнь. И если A и B нормализованы, то выражение упрощается следующим образом:

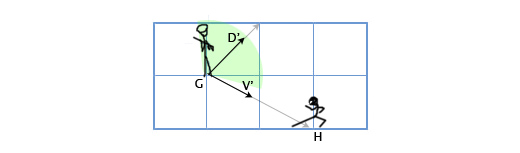
Давайте опять рассмотрим сценарий со стражником. Пусть теперь угол обзора стражника будет равен 120 градусам. Получим нормализованные вектора для направления взгляда стражника (D’) и для направления от стражника к главному герою (V’). Затем определим угол между ними. Если угол более 60 градусов (половина от угла обзора), то главный герой находится вне поля зрения стражника.

D’ = D / |D| = (1, 1) / sqrt(1 2 + 1 2 ) = (1, 1) / sqrt(2) = (0.71, 0.71)
V’ = V / |V| = (2, -1) / sqrt(2 2 + (-1) 2 ) = (2,-1) / sqrt(5) = (0.89, -0.45)

Θ = acos(D’V’) = acos(0.71*0.89 + 0.71*(-0.45)) = acos(0.31) = 72

Угол между центром поля зрения стражника и местоположением главного героя составляет 72 градуса, следовательно стражник его не видит.

Понимаю, что это выглядит довольно сложно, но это потому, что мы всё делаем вручную. В программе это всё довольно просто. Ниже показано как я сделал это в нашей игре Overgrowth с помощью написанных мной С++ библиотек для работы с векторами:

Векторное произведение

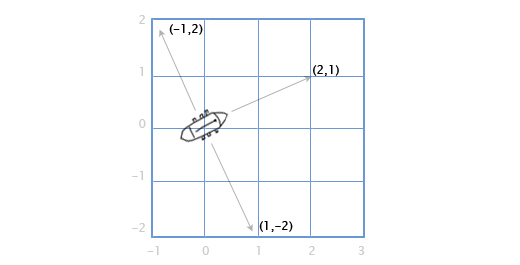
Допустим у нас есть корабль с пушками, которые стреляют в правую и в левую стороны по курсу. Допустим, что лодка расположена вдоль вектора направления (2, 1). В каких направлениях теперь стреляют пушки?

Это довольно просто в двухмерной графике. Чтобы повернуть направление на 90 градусов по часовой стрелке, достаточно поменять местами компоненты вектора, а затем поменять знак второму компоненту.
(a, b) превращается в (b, -a). Следовательно у корабля, расположенного вдоль вектора (2, 1), пушки справа по борту будут стрелять в направлении (1, -2), а пушки с левого борта, будут стрелять в противоположном направлении. Меняем знаки у компонент вектора и получаем (-1, 2).

А что если мы хотим рассчитать это всё для трехмерной графики? Рассмотрим пример с кораблём.
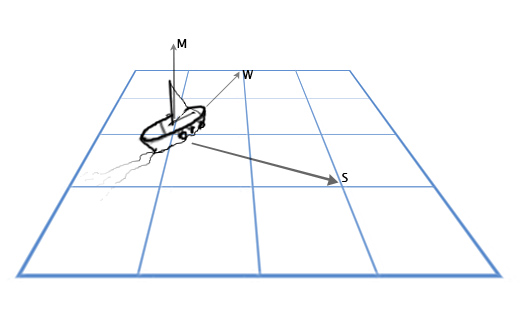
У нас есть вектор мачты M, направленной прямо вверх (0, 1, 0) и направление ветра: север-северо-восток W (1, 0, 2). И мы хотим вычислить вектор направления паруса S, чтобы наилучшим образом «поймать ветер».

Для решения этой задачи мы используем векторное произведение: S = M x W.

Подставим теперь нужные нам значения:

S = MxW = (0, 1, 0) x (1, 0, 2) = ([1*2 — 0*0], [0*1 — 0*2], [0*0 — 1*1]) = (2, 0, -1)

Для расчётов вручную довольно сложно, но для графических и игровых приложений я рекомендую написать функцию, подобную той, что указана ниже и не вдаваться более в детали подобных расчётов.

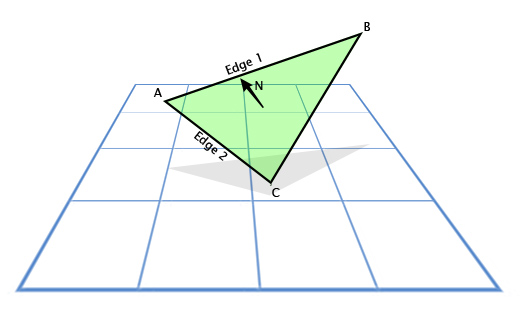
Векторное произведение часто используется в играх, чтобы рассчитать нормали к поверхностям. Направления, в которых «смотрит» та или иная поверхность. Например, рассмотрим треугольник с векторами вершин A, B и С. Как мы найдем направление в котором «смотрит» треугольник, то есть направление перпендикулярное его плоскости? Это кажется сложным, но у нас есть инструмент для решения этой задачи.

Используем вычитание, для определения направления из A в С (C — A), пусть это будет «грань 1» (Edge 1) и направление из A в B (B — A), пусть это будет «грань 2» (Edge 2). А затем применим векторное произведение, чтобы найти вектор, перпендикулярный им обоим, то есть перпендикулярный плоскости треугольника, также называемый «нормалью к плоскости».

Вот так это выглядит в коде:

В играх основное выражение освещённости записывается как N • L, где N — это нормаль к освещаемой поверхности, а L — это нормализованный вектор направления света. В результате поверхность выглядит яркой, когда на неё прямо падает свет, и тёмной, когда этого не происходит.

Теперь перейдем к рассмотрению такого важного для разработчиков игр понятия, как «матрица преобразований» (transformation matrix).

Для начала изучим «строительные блоки» матрицы преобразований.

Базисный вектор

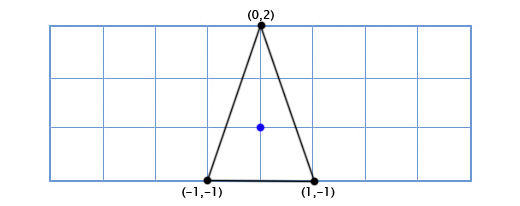
Допустим мы пишем игру Asteroids на очень старом «железе» и нам нужен простой двухмерный космический корабль, который может свободно вращаться в своей плоскости. Модель корабля выглядит так:

Как нам рисовать корабль, когда игрок поворачивает его на произвольный градус, скажем 49 градусов против часовой стрелки. Используя тригонометрию, мы можем написать функцию двухмерного поворота, которая принимает координаты точки и угол поворота, и возвращает координаты смещённой точки:

Применяя эту функцию ко всем трём точкам, мы получим следующую картину:

Операции с синусами и косинусами работают довольно медленно, но так как мы делаем расчёты лишь для трёх точек, это будет нормально работать даже на старом «железе» (прим. переводчика: в случаях, когда предполагается интенсивное использование тригонометрических функций, для ускорения вычислений, в памяти организуют таблицы значений для каждой функции и рассчитывают их во время запуска приложения. Затем при вычислении той или иной тригонометрической функции просто производится обращение к таблице).

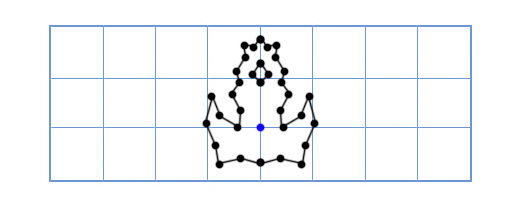
Пусть теперь наш корабль выглядит вот так:

Теперь старый подход будет слишком медленным, так как надо будет поворачивать довольно большое количество точек. Одно из элегантных решений данной проблемы будет звучать так — «Что если вместо поворота каждой точки модели корабля, мы повернём координатную решётку нашей модели?»

Как это работает? Давайте посмотрим внимательнее, что собой представляют координаты.
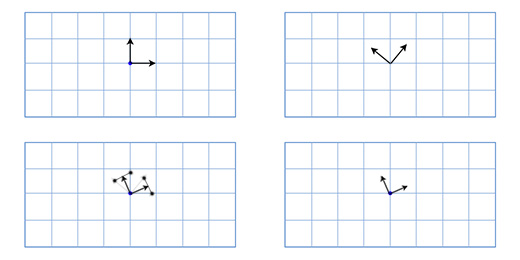
Когда мы говорим о точке с координатами (3, 2), мы говорим, что её местоположение находится в трех шагах от точки отсчёта по координатной оси X, и двух шагах от точки отсчёта по координатной оси Y.

По-умолчанию координатные оси расположены так: вектор координатной оси X (1, 0), вектор координатной оси Y (0, 1). И мы получим расположение: 3(1, 0) + 2(0, 1). Но координатные оси не обязательно должны быть в таком положении. Если мы повернём координатные оси, в это-же время мы повернём все точки в координатной решётке.

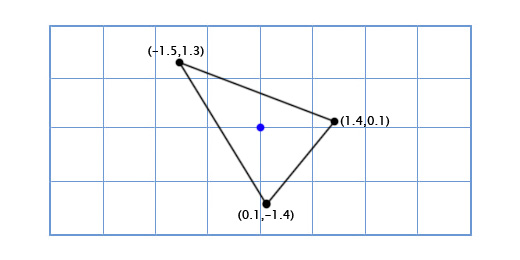
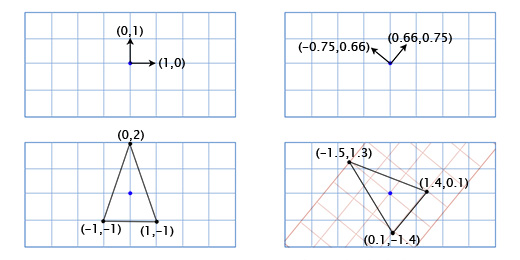
Чтобы получить повернутые оси X и Y мы применим тригонометрические функции, о которых говорили выше. Если мы поворачиваем на 49 градусов, то новая координатная ось X будет получена путём поворота вектора (0, 1) на 49 градусов, а новая координатная ось Y будет получена путём поворота вектора (0, 1) на 49 градусов. Итак вектор новой оси X у нас будет равен (0.66, 0.75), а вектор новой оси Y будет (-0.75, 0.66). Сделаем это вручную для нашей простой модели из трёх точек, чтобы убедиться, что это работает так, как нужно:

Координаты верхней точки (0, 2), что означает, что её новое местоположение находится в 0 на новой (повёрнутой) оси X и 2 на новой оси Y:

0*(0.66,0.75) + 2*(-0.75, 0.66) = (-1.5, 1.3)

Нижняя левая точка (-1, -1), что означает, что её новое местоположение находится в -1 на повернутой оси X, и -1 на повернутой оси Y:

-1*(0.66,0.75) + -1*(-0.75, 0.66) = (0.1, -1.4)

Нижняя правая точка (1, -1), что означает её новое местоположение находится в 1 на повернутой оси X, и -1 на повернутой оси Y

1*(0.66,0.75) + -1*(-0.75, 0.66) = (1.4, 0.1)

Мы показали, как координаты корабля отображаются в другой координатной сетке с повернутыми осями (или «базисными векторами»). Это удобно в нашем случае, так как избавляет нас от необходимости применять тригонометрические преобразования к каждой из точек модели корабля.

Каждый раз, когда мы изменяем базисные вектора (1, 0) и (0, 1) на (a, b) и (c, d), то новая координата точки (x, y) может быть найдена с помощью выражения:

Обычно базисные вектора равны (1, 0) и (0, 1) и мы просто получаем x(1, 0) + y(0, 1) = (x, y), и нет необходимости заботиться об этом дальше. Однако, важно помнить, что мы можем использовать и другие базисные вектора, когда нам это нужно.

Матрицы

Матрицы похожи на двухмерные вектора. Например, типичная 2×2 матрица, может выглядеть так:

Когда вы умножаете матрицу на вектор, вы суммируете скалярное произведение каждой строки с вектором, на который происходит умножение. Например, если мы умножаем вышеприведённую матрицу на вектор (x, y), то мы получаем:

Будучи записанным по-другому, это выражение выглядит так:

Выглядит знакомо, не так-ли? Это в точности такое-же выражение, которые мы использовали для смены базисных векторов. Это означает, что умножая 2×2 матрицу на двухмерный вектор, мы тем самым меняем базисные вектора. Например, если мы вставим стандартные базисные вектора в (1, 0) и (0, 1) в колонки матрицы, то мы получим:

Это единичная матрица, которая не даёт эффекта, который мы можем ожидать от нейтральных базисных векторов, которые мы указали. Если-же мы повернём базисные вектора на 49-градусов, то мы получим:

Эта матрица будет поворачивать двухмерный вектор на 49 градусов против часовой стрелки. Мы можем сделать код нашей игры Asteriods более элегантным, используя матрицы вроде этой. Например, функция поворота нашего корабля может выглядеть так:

Однако, наш код будет ещё более элегантным, если мы сможем также включить в эту матрицу перемещение корабля в пространстве. Тогда у нас будет единая структура данных, которая будет заключать в себе и применять информацию об ориентации объекта и его местоположении в пространстве.

К счастью есть способ добиться этого, хоть это и выглядит не очень элегантно. Если мы хотим переместиться с помощью вектора (e, f), мы лишь включаем его в нашу матрицу преобразования:

И добавляем дополнительную единицу в конец каждого вектора, определяющего местоположение объекта, например так:

Теперь, когда мы перемножаем их, мы получаем:

(a, c, e) • (x, y, 1) + (b, d, f) • (x, y, 1) + (0, 0, 1) • (x, y, 1)

Что, в свою очередь, может быть записано как:

x(a, b) + y(c, d) + (e, f)

Теперь у нас есть полный механизм трансформации, заключённый в одной матрице. Это важно, если не принимать в расчёт элегантность кода, так как с ней мы теперь можем использовать все стандартные манипуляции с матрицами. Например перемножить матрицы, чтобы добавить нужный эффект, или мы можем инвертировать матрицу, чтобы получить прямо противоположное положение объекта.

Трехмерные матрицы

Матрицы в трехмерном пространстве работают так-же как и в двухмерном. Я приводил примеры с двухмерными векторами и матрицами, так как их просто отобразить с помощью дисплея, показывающего двухмерную картинку. Нам просто надо определить три колонки для базисных векторов, вместо двух. Если базисные вектора это (a,b,c), (d,e,f) and (g,h,i) то наша матрица будет выглядеть так:

Если нам нужно перемещение (j,k,l), то мы добавляем дополнительную колонку и строку, как говорили раньше:

И добавляем единицу [1] в вектор, как здесь:

Вращение в двухмерном пространстве

Так как в нашем случае у нас только одна ось вращения (расположенная на дисплее), единственное, что нам надо знать, это угол. Я говорил об этом ранее, упоминая, что мы можем применять тригонометрические функции для реализации функции двухмерного вращения наподобие этой:

Более элегантно это можно выразить в матричной форме. Чтобы определить матрицу, мы можем применить эту функцию к осям (1, 0) и (0, 1) для угла Θ, а затем включить полученные оси в колонки нашей матрицы. Итак, начнём с координатной оси X (1, 0). Если мы применим к ней нашу функцию, мы получим:

(1*cos(Θ) — 0*sin(Θ), 1*sin(Θ) + 0*cos(Θ)) = (cos(Θ), sin(Θ))

Затем, мы включаем координатную ось Y (0, 1). Получим:

(0*cos(Θ) — 1*sin(Θ), 0*sin(Θ) + 1*cos(Θ)) = (-sin(Θ), cos(Θ))

Включаем полученные координатные оси в матрицу, и получаем двухмерную матрицу вращения:

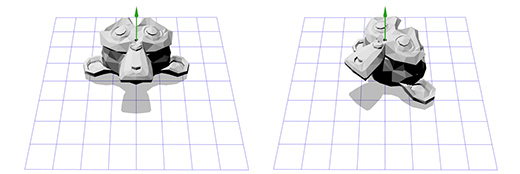
Применим эту матрицу к Сюзанне, мартышке из графического пакета Blender. Угол поворота Θ равен 45 градусов по часовой стрелке.

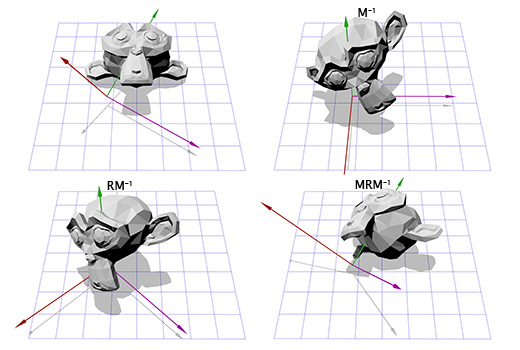
Как видите — это работает. Но что если нам надо осуществить вращение вокруг точки, отличной от (0, 0)?
Например, мы хотим вращать голову мартышки вокруг точки, расположенной в её ухе:

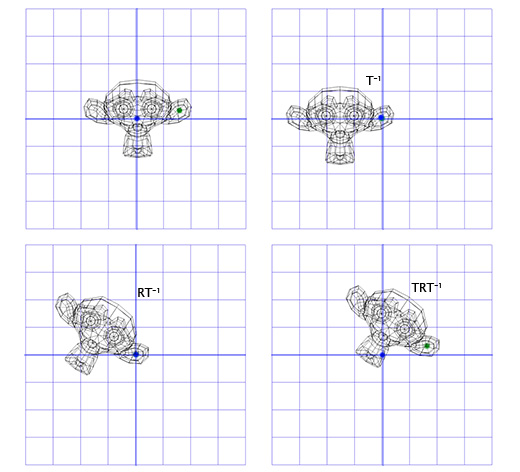
Чтобы сделать это, мы можем начать с создания матрицы перемещения (translation matrix) T, которая перемещает объект из начальной точки в точку вращения в ухе мартышки, и матрицу вращения R, для вращения объекта вокруг начальной точки. Теперь для вращения вокруг точки, расположенной в ухе, мы можем сперва переместить точку в ухе на место начальной точки, с помощью инвертирования матрицы T, записанной как T -1 . Затем, мы вращаем объект вокруг начальной точки, с помощью матрицы R, а затем применяем матрицу T для перемещения точки вращения назад, к своему исходному положению.
Ниже дана иллюстрация к каждому из описанных шагов:

Это важный шаблон, который мы будем применять позднее — применение вращения для двух противоположных трансформаций позволяет нам вращать объект в другом «пространстве». Что очень удобно и полезно.

Теперь рассмотрим трёхмерное вращение.

Трёхмерное вращение

Вращение вокруг оси Z работает по тому-же принципу, что и вращение в двухмерном пространстве. Нам лишь нужно изменить нашу старую матрицу, добавив к ней дополнительную колонку и строку:

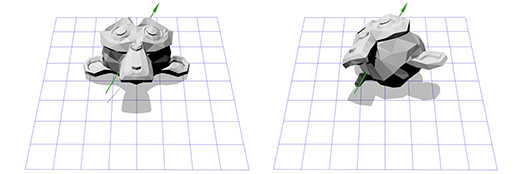
Применим эту матрицу к трехмерной версии Сюзанны, мартышки из пакета Blender. Угол поворота Θ пусть будет равен 45 градусов по часовой стрелке.

То-же самое. Вращение только вокруг оси Z ограничивает нас, как насчёт вращения вокруг произвольной оси?

Вращение, определяемое осью и углом (Axis-angle rotation)

Представление вращения, определяемого осью и углом, также известно как вращение в экспоненциальных координатах, параметризованное вращением двух величин. Вектора, определяющего вращение направляющей оси (прямая линия) и угла, описывающего величину поворота вокруг этой оси. Вращение осуществляется согласно правилу правой руки.

Итак, вращение задаётся двумя параметрами (axis, angle), где axis — вектор оси вращения, а angle — угол вращения. Этот приём довольно прост и являет собой отправную точку для множества других операций вращения, с которыми я работаю. Как практически применить вращение, определяемое осью и углом?

Допустим мы имеем дело с осью вращения, показанной на рисунке ниже:

Мы знаем как вращать объект вокруг оси Z, и мы знаем как вращать объект в других пространствах. Итак, нам лишь надо создать пространство, где наша ось вращения будет являться осью Z. И если эта ось будет осью Z, то что будет являться осями X и Y? Займемся вычислениями сейчас.

Чтобы создать новые оси X и Y нам нужно лишь выбрать два вектора, которые перпендикулярны новой оси Z и перпендикулярны друг другу. Мы уже говорили ранее о векторном умножении, которое берёт два вектора и даёт в итоге перпендикулярный им вектор.

У нас есть один вектор сейчас, это ось вращения, назовём его A. Возьмём теперь случайный другой вектор B, который находится не в том-же направлении, что и вектор A. Пусть это будет (0, 0, 1) к примеру.

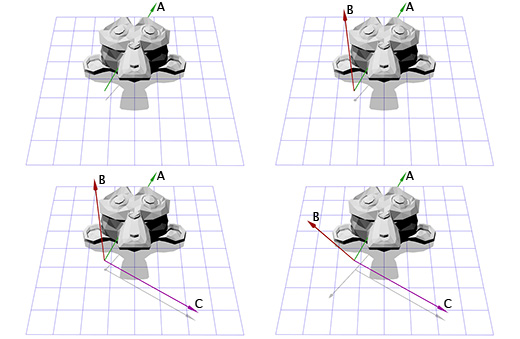
Теперь мы имеем ось вращения A и случайный вектор B, мы можем получить нормаль C, через векторное произведение A и B. С перпендикулярен векторам A и B. Теперь мы делаем вектор B перпендикулярным векторам A и C через их векторное произведение. И всё, у нас есть все нужные нам оси координат.

На словах это звучит сложно, но довольно просто выглядит в коде или будучи показанным в картинках.
Ниже показано, как это выглядит в коде:

Тут показана иллюстрация для каждого шага:

Теперь, имея информацию о новых координатных осях, мы можем составить матрицу M, включив каждую ось как колонку в эту матрицу. Нам надо убедиться, что вектор A является третьей колонкой, чтобы он был нашей новой осью координат Z.

Теперь это похоже на то, что мы делали для поворота в двухмерном пространстве. Мы можем применить инвертированную матрицу M, чтобы переместиться в новую систему координат, затем произвести вращение, согласно матрице R, чтобы повернуть объект вокруг оси Z, затем применить матрицу M, чтобы вернуться в исходное координатное пространство.

Теперь мы можем вращать объект вокруг произвольной оси. В конце концов мы можем просто создать матрицу T = T = M -1 RM и использовать её много раз, без дополнительных усилий с нашей стороны. Есть более эффективные способы конвертирования вращений, определяемых осью и углом во вращения, определяемые матрицами. Просто описанный нами подход показывает многое из того, о чём мы говорили ранее.

Вращение, определяемое осью и углом, возможно, самый интуитивно понятный способ. Применяя его, очень легко инвертировать поворот, поменяв знак у угла, и легко интерполировать, путём интерполяции угла. Однако тут есть серьёзное ограничение, и заключается оно в том, что такое вращение не является суммирующим. То есть вы не можете комбинировать два вращения, определяемых осью и углом в третье.
Вращение, определяемое осью и углом — хороший способ для начала, но оно должно быть преобразовано во что-то другое, чтобы использоваться в более сложных случаях.

Эйлеровские углы

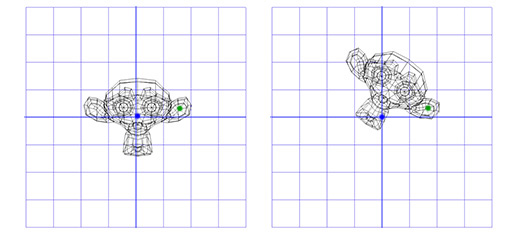
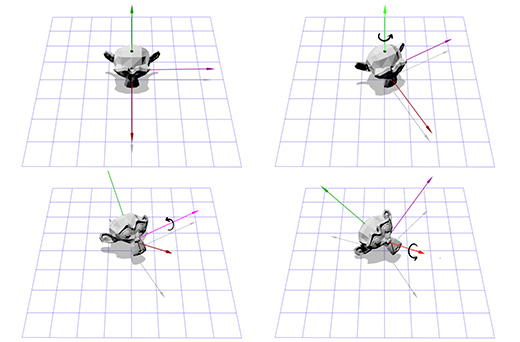
Эйлеровские углы представляют собой другой способ вращения, заключающийся в трёх вложенных вращениях относительно осей X, Y и Z. Вы, возможно, сталкивались с их применением в играх, где камера показывает действие от первого лица, либо от третьего лица.

Допустим вы играете в шутер от первого лица и вы повернулись на 30 градусов влево, а затем посмотрели на 40 градусов вверх. В конце-концов в вас стреляют, попадают, и, в результате удара, камера поворачивается вокруг своей оси на 45 градусов. Ниже показано вращение с помощью углов Эйлера (30, 40, 45).

Углы Эйлера — удобное и простое в управлении средство. Но у этого способа есть два недостатка.

Первый, это вероятность возникновения ситуации под названием «блокировка оси» или «шарнирный замок» (gimbal lock). Представьте, что вы играете в шутер от первого лица, где вы можете посмотреть влево, вправо, вверх и вниз или повернуть камеру вокруг зрительной оси. Теперь представьте, что вы смотрите прямо вверх. В этой ситуации попытка взглянуть налево или направо будет аналогична попытке вращения камеры. Всё что мы можем вы этом случае, это вращать камеру вокруг своей оси, либо посмотреть вниз. Как вы можете представить, это ограничение делает непрактичным применение углов Эйлера в лётных симуляторах.

Второе — интерполяция между двумя эйлеровскими углами вращения не даёт кратчайшего пути между ними.
Например, у вас две интерполяции между двумя одинаковыми вращениями. Первая использует интерполяцию эйлеровского угла, вторая использует сферическую линейную интерполяцию (spherical linear interpolation (SLERP)), чтобы найти кратчайший путь.

Итак, что-же больше подойдет для интерполяции вращений? Может быть матрицы?

Вращение с помощью матриц

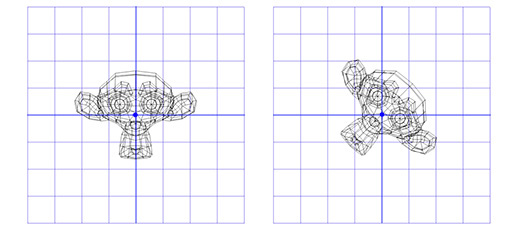
Как мы уже говорили ранее, матрицы вращения хранят в себе информацию о трёх осях. Это означает, что интерполяция между двумя матрицами лишь линейно интерполирует каждую ось. В результате это даёт нам эффективный путь, то так-же привносит новые проблемы. Например, тут показаны два вращения и одно интерполированное полу-вращение:

Как вы можете заметить, интерполированное вращение значительно меньше, чем любое из исходных вращений, и две оси более не перпендикулярны друг другу. Это логично, если вдуматься — середина отрезка, соединяющего любые две точки на сфере будет расположена ближе к центру сферы.

Это в свою очередь порождает известный «эффект фантика» (candy wrapper effect), при применении скелетной анимации. Ниже показана демонстрация этого эффекта на примере кролика из нашей игры Overgrowth (прим. переводчика: обратите внимание на середину туловища кролика).

Вращение, основанное на матричных операциях, очень полезно, так как они могут аккумулировать вращения без всяких проблем, вроде блокировки оси (gimbal lock), и может очень эффективно применяться к точкам сцены. Вот почему поддержка вращения на матрицах встроена в графические карты. Для любого типа трёхмерной графики матричный формат вращения — это всегда итоговый применяемый способ.

Однако, как мы уже знаем, матрицы не очень хорошо интерполируются, и они не столь интуитивно понятны.

Итак, остался только один главный формат вращения. Последний, но тем не менее, важный.

Кватернионы

Что-же такое кватернионы? Если очень кратко, то это альтернативный вариант вращения, основанный на оси и угле (axis-angle rotation), который существует в пространстве.

Подобно матрицам они могут аккумулировать вращения, то есть вы можете составлять из них цепочку вращений, без опаски получить блокировку оси (gimbal lock). И в то-же время, в отличие от матриц, они могут хорошо интерполироваться из одного положения в другое.

Являются-ли кватернионы лучшим решением, нежели остальные способы вращений (rotation formats)?
На сегодняшний день они комбинируют все сильные стороны других способов вращений. Но у них есть два слабых места, рассмотрев которые, мы придём к выводу, что кватернионы лучше использовать для промежуточных вращений. Итак, каковы недостатки кватернионов.

Во-первых кватернионы непросто отобразить на трёхмерном пространстве. И мы вынуждены всегда реализовывать вращение более простым способом, а затем конвертировать его. Во-вторых, кватернионы не могут эффективно вращать точки, и мы вынуждены конвертировать их в матрицы, чтобы повернуть значительное количество точек.

Это означает, что вы скорее всего не начнете или не закончите серию вращений с помощью кватернионов. Но с их помощью можно реализовать промежуточные вращения более эффективно, нежели при применении любого другого подхода.

«Внутренняя кухня» механизма кватернионов не очень понятна и не интересна мне. И, возможно, не будет интересна и вам, если только вы не математик. И я советую вам найти библиотеки, которые работают с кватернионами, чтобы облегчить вам решение ваших задач с их помощью.

Математические библиотеки «Bullet» или «Blender» будут хорошим вариантом для начала.

Видео:РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ 10 и 11 классСкачать

Векторы. Метод координат. Угол между прямыми, плоскостями. Расстояние от точки до плоскости, между скрещивающимися прямыми

(<color<textbf>>)
(bullet) Если в пространстве заданы две точки (A(x_1;y_1;z_1)) и (B(x_2;y_2;z_2)) , то вектор (overrightarrow) имеет координаты [overrightarrow = ]
(bullet) Если в пространстве заданы два вектора (vec =) и (vec= ) , то:

(qquad blacktriangleright) разность этих векторов (vec-vec=)

(bullet) Справедливы следующие утверждения:

I. Скалярное произведение ненулевых векторов (их длины не равны нулю) равно нулю тогда и только тогда, когда они перпендикулярны: [(vec, vec)=0 quadLeftrightarrowquad vecperp vec]

II. Длина вектора равна квадратному корню из скалярного произведения вектора на себя: [|vec|=sqrt]

III. Переместительный закон: [(vec, vec)=(vec, vec)]

(<color<textbf>>)
(bullet) Если (vec=) – нормаль к плоскости, то уравнение плоскости имеет вид [ax+by+cz+d=0] Для того, чтобы найти (d) , нужно подставить в уравнение плоскости вместо (x, y, z) координаты любой точки, лежащей в этой плоскости. Пример: если (vec=) – нормаль к плоскости, (O(4;5;6)) – точка из плоскости, то справедливо: (1cdot 4+2cdot 5+3cdot 6+d=0) , откуда (d=-32) , следовательно, уравнение плоскости имеет вид (x+2y+3z-32=0) . (bullet) Уравнение плоскости можно составить, используя три точки из плоскости, не лежащие на одной прямой.
Пусть (A(1;0;0), B(0;3;4), C(2;0;5)) – точки из плоскости. Тогда уравнение плоскости можно найти, решив систему: [begin 1cdot a+0cdot b+0cdot c+d=0\ 0cdot a+3cdot b+4cdot c+d=0\ 2cdot a+0cdot b+5cdot c+d=0end quadRightarrowquad begin d=-a\ 3b+4c-a=0\ a+5c=0endquadRightarrowquad begin d=-a\ a=-5c\ b=-3cendquadRightarrowquadbegina=-5c\ b=-3c\ d=5cend] Следовательно, уравнение плоскости имеет вид: [-5ccdot x-3ccdot y+ccdot z+5c=0] Можно разделить обе части на (c) , так как (cne 0) (иначе (a=b=c=d=0) ), следовательно, уравнение плоскости имеет вид [-5x-3y+z+5=0]

(<color<textbf>>)
(bullet) Если (M(x_0;y_0;z_0)) — некоторая точка вне плоскости (phi) , (ax+by+cz+d=0) — уравнение плоскости (phi) , то расстояние от точки (M) до плоскости (phi) ищется по формуле: [rho(M, phi)=dfrac<sqrt >]
(bullet) Для того, чтобы найти расстояние между скрещивающимися прямыми, нужно
— построить плоскость, проходящую через одну из них и параллельную другой;
— найти уравнение этой плоскости;
— найти расстояние от любой точки первой прямой до этой плоскости.