Что такое полюс окружности

Сферическая геометрия – математическая дисциплина, изучающая геометрические образы (точки, линии, фигуры), находящиеся на сфере, и соотношения между ними.

По-видимому, первым обращением человечества к тому, что потом получит название сферической геометрии, была планетарная теория греческого математика Евдокса (ок. 408–355), одного из участников Академии Платона. Это была попытка объяснить движение планет вокруг Земли с помощью четырех вращающихся концентрических сфер, каждая из которых имела особую ось вращения с концами, закрепленными на охватывающей сфере, к которой, в свою очередь, были «прибиты» звезды. Таким образом объяснялись замысловатые траектории планет (в переводе с греческого «планета» – блуждающая). Именно благодаря такой модели древнегреческие ученые умели достаточно точно описывать и предсказывать движения планет. Это было необходимо, например, в мореплавании, а так же во многих других «земных» задачах, где нужно было учитывать, что Земля – не плоский блин, покоящийся на трех китах. Значительный вклад в сферическую геометрию внес Менелай из Александрии (ок. 100 н.э.). Его труд Сферика стал вершиной достижений греков в этой области. В Сферике рассматриваются сферические треугольники – предмет, которого нет у Евклида. Менелай перенес на сферу евклидову теорию плоских треугольников и в числе прочего получил условие, при котором три точки на сторонах сферического треугольника или их продолжениях лежат на одной прямой. Соответствующая теорема для плоскости в то время была уже широко известна, однако в историю геометрии она вошла именно как теорема Менелая, причем, в отличие от Птолемея (ок. 150), у которого в работах немало вычислений, трактат Менелая геометричен строго в духе евклидовой традиции.

Основные положения сферической геометрии

Всякая плоскость, пересекающая сферу, дает в сечении окружность. Если плоскость проходит через центр сферы, то в сечении получается так называемый большой круг. Через любые две точки на сфере, кроме диаметрально противоположных, можно провести единственный большой круг. (На глобусе примером большого круга служит экватор и все меридианы.) Через диаметрально противоположные точки проходит же бесконечное количество больших кругов. Меньшая дуга AmB (рис. 1) большого круга является кратчайшей из всех линий на сфере, соединяющих заданные точки. Такая линия называется геодезической. Геодезические линии играют на сфере ту же роль, что и прямые в планиметрии. Многие положения геометрии на плоскости справедливы и на сфере, но, в отличие от плоскости, две сферические прямые пересекаются в двух диаметрально противоположных точках. Таким образом, в сферической геометрии просто не существует понятия параллельности. Еще одно отличие – сферическая прямая замкнута, т.е. двигаясь по ней в одном и том же направлении, мы вернемся в исходную точку, точка не разбивает прямую на две части. И еще один удивительный с точки зрения планиметрии факт – треугольник на сфере может иметь все три прямых угла.

Рисунок 1 – Сферическая прямая

Прямые, отрезки, расстояния и углы на сфере

Прямыми на сфере считаются большие окружности. Если две точки принадлежат большой окружности, то длина меньшей из дуг, соединяющих эти точки, определяется как сферическое расстояние между этими точками, а сама дуга – как сферический отрезок. Диаметрально противоположные точки соединены бесконечным числом сферических отрезков – больших полуокружностей. Длина сферического отрезка определяется через радианную меру центрального угла α и радиус сферы R (рис. 2), по формуле длины дуги она равна R α. Любая точка С сферического отрезка АВ разбивает его на два, и сумма их сферических длин, как и в планиметрии, равна длине всего отрезка, т.е. АОС + СОВ = АОВ. Для любой же точки D вне отрезка АВ имеет место сферическое неравенство треугольника : сумма сферических расстояний от D до А и от D до В больше АВ, т.е. AOD + DOB > AOB, – полное соответствие между сферической и плоской геометриями. Неравенство треугольника – одно из основополагающих в сферической геометрии, из него следует, что, как и в планиметрии, сферический отрезок короче любой сферической ломаной, а значит, и любой кривой на сфере, соединяющей его концы.

Рисунок 2 – Длина сферического отрезка

Таким же образом на сферу можно перенести и многие другие понятия планиметрии, в частности те, которые можно выразить через расстояния. Например, сферическая окружность – множество точек сферы, равноудаленных от заданной точки Р. Легко показать, что окружность лежит в плоскости, перпендикулярной диаметру сферы РР` (рис. 3), т.е. это обычная плоская окружность с центром на диаметре РР`. Но сферических центров у нее два: Р и Р`. Эти центры принято называть полюсами. Если обратиться к глобусу, то можно видеть, что идет речь именно о таких окружностях, как параллели, и сферическими центрами всех параллелей являются Северный и Южный полюса. Если диаметр r сферической окружности равен π/2, то сферическая окружность превращается в сферическую прямую. (На глобусе – экватор). В этом случае такую окружность называют полярой каждой из точек Р и P`.

Рисунок 3 – Сферическая окружность

Одним из важнейших понятий в геометрии является равенство фигур. Фигуры считаются равными, если одну на другую можно отобразить таким образом (поворотом и переносом), что сохранятся расстояния. Это верно и для сферической геометрии.

Углы на сфере определяются следующим образом. При пересечении двух сферических прямых a и b на сфере образуются четыре сферических двуугольника, подобно тому, как две пересекающиеся прямые на плоскости разбивают ее на четыре плоских угла (рис. 4). Каждому из двуугольников соответствует двугранный угол, образованный диаметральными плоскостями, содержащими a и b. А угол между сферическими прямыми равен меньшему из углов образуемых ими двуугольников.

Рисунок 4 – Углы на сфере

Отметим так же, что угол ABC, образованный на сфере двумя дугами большого круга, измеряют углом A`BC` между касательными к соответствующим дугам в точке В (рис. 5) или двугранным углом, образованным диаметральными плоскостями, содержащими сферические отрезки АВ и ВС.

Рисунок 5 – Угол на сфере, образованный дугами большого круга

Точно так же, как и в стереометрии, каждой точке сферы сопоставляется луч, проведенный из центра сферы в эту точку, а любой фигуре на сфере – объединение всех пересекающих ее лучей. Так, сферической прямой соответствует содержащая ее диаметральная плоскость, сферическому отрезку – плоский угол, двуугольнику – двугранный угол, сферической окружности – коническая поверхность, ось которой проходит через полюсы окружности.

Многогранный угол с вершиной в центре сферы пересекает сферу по сферическому многоугольнику (рис. 6). Это область на сфере, ограниченная ломаной из сферических отрезков. Звенья ломаной – стороны сферического многоугольника. Их длины равны величинам соответствующих плоских углов многогранного угла, а величина угла при любой вершине А равна величине двугранного угла при ребре ОА.

Рисунок 6 – Многогранный угол

Сферический треугольник

Среди всех сферических многоугольников наибольший интерес представляет сферический треугольник. Три больших окружности, пересекаясь попарно в двух точках, образуют на сфере восемь сферических треугольников. Зная элементы (стороны и углы) одного из них, можно определить элементы все остальных, поэтому рассматривают соотношения между элементами одного из них, того, у которого все стороны меньше половины большой окружности. Стороны треугольника измеряются плоскими углами трехгранного угла ОАВС, углы треугольника – двугранными углами того же трехгранного угла (рис. 7).

Рисунок 7 – Трехгранный угол

Многие свойства сферического треугольника (а они одновременно являются и свойствами трехгранных углов) почти полностью повторяют свойства обычного треугольника. Среди них – неравенство треугольника, которое на языке трехгранных углов гласит, что любой плоский угол трёхгранного угла меньше суммы двух других. Или, например, три признака равенства треугольников. Все планиметрические следствия упомянутых теорем вместе с их доказательствами остаются справедливыми на сфере. Так, множество точек, равноудаленных от концов отрезка, будет и на сфере перпендикулярной к нему прямой, проходящей через его середину, откуда следует, что серединные перпендикуляры к сторонам сферического треугольника AВС имеют общую точку, точнее, две диаметрально противоположные общие точки Р и Р`, являющиеся полюсами его единственной описанной окружности (рис. 8). В стереометрии это означает, что около любого трёхгранного угла можно описать конус. Легко перенести на сферу и теорему о том, что биссектрисы треугольника пересекаются в центре его вписанной окружности.

Рисунок 8 – Описанная окружность сферического треугольника

Теоремы о пересечении высот и медиан также остаются верными, но их обычные доказательства в планиметрии прямо или косвенно используют параллельность, которой, на сфере нет, и потому проще доказать их заново, на языке стереометрии. Рис. 9 иллюстрирует доказательство сферической теоремы о медианах: плоскости, содержащие медианы сферического треугольника АВС, пересекают плоский треугольник с теми же вершинами по его обычным медианам, следовательно, все они содержат радиус сферы, проходящий через точку пересечения плоских медиан. Конец радиуса и будет общей точкой трех «сферических» медиан.

Рисунок 9 – Доказательство сферической теоремы о медианах

Свойства сферических треугольников во многом отличаются от свойств треугольников на плоскости. Так, к известным трем случаям равенства прямолинейных треугольников добавляется еще и четвертый: два треугольника АВС и А`В`С` равны, если равны соответственно три угла РА = РА`, РВ = РВ`, РС = РС`. Таким образом, на сфере не существует подобных треугольников, более того, в сферической геометрии нет самого понятия подобия, т.к. не существует преобразований, изменяющих все расстояния в одинаковое (не равное 1) число раз. Эти особенности связаны с нарушением евклидовой аксиомы о параллельных прямых и также присущи геометрии Лобачевского. Треугольники, имеющие равные элементы и различную ориентацию, называются симметричными, таковы, например, треугольники АС`С и ВСС` (рис. 10).

Рисунок 10 – Симметричные треугольники

Сумма углов всякого сферического треугольника всегда больше 180°. Разность А + В + С – π = d (измеряемая в радианах) – величина положительная и называется сферическим избытком данного сферического треугольника. Площадь сферического треугольника: S = R 2 d где R – радиус сферы, а d – сферический избыток. Эта формула впервые была опубликована голландцем А.Жираром в 1629 и названа его именем.

Если рассматривать двуугольник с углом a, то при 226 = 2π/n (n – целое число) сферу можно разрезать ровно на n копий такого двуугольника, а площадь сферы равна 4πR 2 = 4π при R = 1, поэтому площадь двуугольника равна 4π/n = 2α. Эта формула верна и при α = 2πm/n и, следовательно, верна для всех a. Если продолжить стороны сферического треугольника АВС и выразить площадь сферы через площади образующихся при этом двуугольников с углами А, В, С и его собственную площадь, то можно прийти к вышеприведенной формуле Жирара.

Координаты на сфере

Каждая точка на сфере вполне определяется заданием двух чисел; эти числа (координаты) определяются следующим образом (рис. 11). Фиксируется некоторый большой круг QQ` (экватор), одна из двух точек пересечения диаметра сферы PP`, перпендикулярного к плоскости экватора, с поверхностью сферы, например Р (полюс), и один из больших полукругов PAP`, выходящих из полюса (первый меридиан). Большие полукруги, выходящие из P, называются меридианами, малые круги, параллельные экватору, такие, как LL`, – параллелями. В качестве одной из координат точки M на сфере принимается угол q = POM (высота точки), в качестве второй – угол j = AON между первым меридианом и меридианом, проходящим через точку M (долгота точки, отсчитываемая против часовой стрелки).

Рисунок 11 – Координаты точки на сфере

В географии (на глобусе) в качестве первого меридиана принято использовать Гринвичский меридиан, проходящий через главный зал Гринвичской обсерватории (Гринвич – городской округ Лондона), он разделяет Землю на Восточное и Западное полушария, соответственно и долгота бывает восточной либо западной и измеряется от 0 до 180° в обе стороны от Гринвича. А вместо высоты точки в географии принято использовать широту, т.е. угол NOM = 90° – θ, отсчитываемый от экватора. Т.к. экватор делит Землю на Северное и Южное полушария, то и широта бывает северной либо южной и изменяется от 0 до 90°.

Видео:Тропики и полярные кругиСкачать

ПОЛЮСЫ И ПОЛЯРЫ ОТНОСИТЕЛЬНО ОКРУЖНОСТИ

Видео:Полярная система координатСкачать

ПОЛЮСЫ И ПОЛЯРЫ ОТНОСИТЕЛЬНО ОКРУЖНОСТИ

ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

204. Теорема. Если через точку а, взятую в плоскости круга,
провести произвольную секущую, пересекающую окружность
в точках М и N, то геометрическое место точек Р, гармонически
сопряжённых с точкой а относительно
точек М и N, есть
прямая линия (черт. 191).

Действительно, середина /
отрезка аР удовлетворяет
(п. 189) равенству
1а? = 1М • IN.
Эта точка I принадлежит,
таким образом, определённой
прямой—радикальной оси данной
окружности и точки а
(п. 136, примечание 1°). Черт. 191.
Точка Р опишет прямую,
гомотетичную этой прямой относительно точки а, причём коэффициент
подобия равен 2 .
Обратно, какая-либо точка Р прямой, таким образом определённой,
принадлежит рассматриваемому геометрическому месту, если луч
аР пересекает окружность (что всегда имеет место, если точка а
лежит внутри окружности).
Эта прямая — геометрическое место точек Р—называется полярой
точки а относительно окружности, а точка а — полюсом этой
прямой.
Следствие. Поляра точки а перпендикулярна к прямой, соединяющей
эту точку с центром О окружности, и пересекает эту
прямую в некоторой точке Н, которая лежит по ту же сторону от
центра, как и точка а, и определяется равенством
O a — O H = R v (5)
где R — радиус окружности.
Действительно, это равенство показывает, что точки а и Н делят
гармонически диаметр, лежащий на прямой Оа.
Из отрезков Оа и ОН один больше, а другой меньше радиуса,
таккак радиус является их средним пропорциональным; следовательно,
поляра пересекает окружность или не пересекает её, смотря по
тому, лежит ли полюс вне или внутри окружности.

193 ПОЛЮСЫ И ПОЛЯРЫ ОТНОСИТЕЛЬНО ОКРУЖНОСТИ.

Определение поляры и её построение

Если точка а лежит вне окружности, то полярой этой точки
служит хорда, соединяющая точки прикосновения касательных,
проходящих через эту точку.
Действительно, рассуждения, которыми мы пользовались для обоснования
существования поляры, остаются верными, если секущая
aMN на чертеже 191 обращается в касательную, причём обе точки
М и N совпадут с точкой прикосновения Т этой касательной. Точка
Р будет в этом случае совпадать с точкой Т, и поляра должна проходить
через эту точку.
Если точка а лежит на окружности, то определение поляры
как геометрического места точек, собственно говоря, теряет свой
смысл1); но мы можем найти эту прямую с помощью доказанного выше
следствия: точка Н в данном случае совпадает с точкой а, и полярой
является касательная в этой точке.
Отрезок ОН, определённый равенством (5), бесконечно велик
только в том случае, когда точка а совпадает с точкой О; только
в этом случае соответствующее построение невозможно. Впрочем,
d priori очевидно, что поляра удаляется при этом в бесконечность, так
как точка О есть середина всех хорд, проходящих через эту точку.
То же самое равенство позволяет, обратно, найти полюс, если
известна поляра. Проводим из центра перпендикуляр ОН к данной
поляре и откладываем на прямой ОН отрезок Оа, определяемый равенством
(5). Это невозможно сделать, только если ОН равно нулю,
т. е. если данная прямая есть один из диаметров окружности:
при этом полюс удаляется в бесконечность в направлении, перпендикулярном
к диаметру.

194 ПОЛЮСЫ И ПОЛЯРЫ ОТНОСИТЕЛЬНО ОКРУЖНОСТИ.

Определение поляры и её построение

205. Наиболее важным является следующее свойство поляры.
Теорема. Если точка а лежит на поляре точки Ь, то, обратноу
последняя лежит на поляре точки а.
Точки а и b называются в этом случае сопряжёнными относительно
окружности. Их поляры, т. е. две прямые, каждая из которых
проходит через полюс другой, точно также называются сопряжёнными.
Так как точка а (черт. 192) лежит на поляре точки b, то её
проекция на ОЬ есть такая точка К, что OK * Ob = R2. Пусть точка
Н—проекция точки b на Оа тогда четырёхугольник аНЬК можно
вписать в окружность (а именно в окружность, построенную на отрезке
ab как на диаметре), и мы имеем:
O H — O a = O K — O b = R
Следовательно, прямая Н Ь — поляра точки а .
*) Одна из точек пересечения М и iV всё время совпадает с точкой я,
й, следовательно, точка Р также, вообще говоря, совпадает с точкой а ;
однако, если секущая обращается в касательную, то обе точки М и N совпадают
с точкой а, и положение . Точки Р на этой касательной неопреде-
лено.

194 Теорема о сопряжённых точках.

П р и м е ч а н и е . Теорема очевидна, если прямая ab пересекает
окружность, так как в этом случае условие и заключение выражают
одно и то же, а именно, что окружность делит отрезок ab гармонически.
206. Предыдущая теорема позволяет переходить от свойств некоторой
фигуры (F) к свойствам другой фигуры (F’), которую мы
сейчас определим и которая называется фигурой взаимно-полярной
(или коррелятивной) данной.
Пусть F—фигура, состоящая из любого числа точек и прямых1).
Каждой точке а этой фигуры поставим в соответствие прямую А, а
именно—поляру точки а относительно некоторой окружности, выбранной
раз навсегда и называемой направляющей
окружностью. Каждой
прямой В фигуры (F) поставим
в соответствие точку Ьу а именно —
полюс этой прямой относительно направляющей
окружности. Прямые
А и точки b образуют фигуру ( F ) ,
взаимно-полярную фигуре (F ).
В силу предыдущей теоремы будем
иметь следующее предложение:
Если прямая В фигуры (F ) проходит
через точку а, то соответствующая
точка b фигуры ( F r ) лежит на Черт. 192.
прямой А, соответствующей точке а.
Следовательно, если прямая фигуры (F) вращается около неподвижной
точки, то соответствующая точка фигуры (Fr) описывает
прямую линию, и обратно.

Или иначе, если три прямые линии фигуры (F) проходят через
одну точку, то соответствующие им точки фигуры (.F) лежат
на одной прямой, и обратно.
207. Предположим, например, что фигура (.F) есть фигура п. 195
(черт. 186), образованная такими двумя треугольниками abc и arbrc
что прямые аа ЬЪ ссг проходят через одну точку о. Поляры Л, В,
С, А В С точек а, b, с, а Ь с образуют два новых треугольника.
Прямым аа!, ЬЪ ссг соответствуют точки пересечения сторон
А, Аг; В, Вг С, С; так как первые три прямые проходят через
одну точку, то последние три точки лежат на одной прямой.
Обратно, каждую пару треугольников, стороны которых соответствуют
друг другу так, что точки пересечения соответственных
сторон лежат на одной прямой, можно рассматривать как фигуру,
взаимно-полярную паре треугольников, аналогичных треугольникам
abc и агЬТс’
* ) Определение взаимно-полярных фигур распространяется с помощью
соображений, которые мы будем рассматривать в геометрии пространства
и на фигуры, содержащие кривые линии.

195 Теорема о сопряжённых точках

Мы доказали (п. 195), что точки пересечения соответственных
сторон треугольников abc, a!brcr лежат на одной прямой; следовательно,
прямые, которые соответствуют этим точкам, т. е. прямые,
которые соединяют соответственные вершины треугольников, образованных
прямыми Л, В, С; Л’, В С’пересекаются в одной точке. Другими
словами, теорема, обратная теореме, доказанной в п. 195,
верна.

196 Теорема о сопряжённых точках

Определение поляры и её построение

208. Предположим теперь, что фигура (F) — шестиугольник, вписанный
в окружность; пусть Л, В, С, Ь, Е, F (черт. 193) — стороны
этого шестиугольника.
Примем окружность, описанную около шестиугольника, за направляющую
окружность; поляры вершин шестиугольника будут касательными
в этих точках и будут попарно пересекаться
в точках а, b, с, d, е, /—полюсах
сторон Л, В, С, Д Д F. Эти последние
точки будут вершинами шестиугольника, описанного
около окружности. Обратно, всякий
шестиугольник, описанный около окружности,
можно рассматривать как взаимно-полярный
некоторому вписанному шестиугольнику.
Но мы доказали, что во вписанном шестиугольнике
точки пересечения Л, D; В, Е
Че т С, F лежат на одной прямой (п. 196).

Таким
образом, мы имеем теорему Б р и а н ш о н а :
Во всяком шестиугольнике abcdef, описанном около окружности,
диагонали, соединяющие противоположные вершины, пересекаются
в одной точке.
Точно так же предельный случай, относящийся к вписанному
треугольнику (п. 196, примечание), даёт:
Во всяком треугольнике, описанном около окружности, прямые,
соединяющие каждую вершину с точкой касания противоположной
стороны, пересекаются в одной точке.

196 Взаимно-полярные фигуры

209. Мы знаем, что соответствует в фигуре (F) трём лежащим
на одной прямой точкам или трём пересекающимся в одной точке
прямым фигуры (Z7); эти свойства (т. е. свойство трёх точек лежать
на одной прямой и свойство трёх прямых проходить через одну точку)
называются дескриптивными в отличие от тех, в которых фигурируют
значения тех или других величин и которые называются метрическими.
Мы рассмотрим теперь законы преобразования некоторых
из последних.
Прежде всего, если две прямые линии фигуры F параллельны,
то их полюсы лежат на одной прямой с центром О направляющей
окружности (на диаметре, перпендикулярном к направлению
параллельных прямых), и обратно.
Например, мы могли бы, таким образом, легко доказать теорему
п. 195, рассмотрев фигуру, взаимно-полярную данной относительно
направляющей окружности с центром в точке о (черт. 186).

196 Преобразование метрических свойств

Точкам а, о! b> V с, с’ соответствовали бы прямые, попарно
параллельные, и, следовательно, образующие два гомотетичных треугольника,
так что прямые, соединяющие соответственные вершины
двух последних треугольников, пересекались бы в одной точке; отсюда,
возвращаясь к первоначальной фигуре, мы получили бы требуемое
заключение.
Вообще, угол между двумя прямыми равен углу, под которым
отрезок, соединяющий их полюсы, виден из центра О направляющей
окружности (или углу, ему пополнительному), так как эти
два угла имеют соответственно перпендикулярные стороны (черт. 192).
Преобразуем, например, теорему о высотах треугольника (п. 53).
Вершинам а, b, с какого-либо треугольника соответствуют стороны
Л, В, С нового треугольника. Высота, опущенная из точки а, даёт
в новой фигуре точку, лежащую, с одной стороны, на прямой Л и,
с другой стороны, на прямой, проходящей через центр направляющей
окружности О и перпендикулярной к прямой, которая проходит через
точку О и соответствующую вершину (точку пересечения сторон В и С)
нового треугольника.
Так как три высоты треугольника abc пересекаются в одной и
той же точке, мы имеем *) следующее предложение:
Если через какую-либо точку О, лежащую в плоскости треугольника,
провести прямые, перпендикулярные к прямым, которые
соединяют эту точку с тремя вершинами, то проведённые
прямые пересекают соответствующие стороны в трёх точках,
лежащих на одной прямой.
210, Сложное отношение четырёх прямых Dv D%, Z)3, Z) 4 пересекающихся
в точке а, равно сложному отношению их полюсов
du ^2, d3, d4, так как четвёрки прямых ( O d v Od%, Od%, Od4) и ( D l y
Z)2, D%, Z)4), где О — центр направляющей окружности, равны: они
получаются одна из другой, если переместить первую параллельно самой
себе из точки О в точку а и повернуть её затем на прямой
угол около этой точки. Следовательно, обе четвёрки имеют одно и
то же сложное отношение.
В частности, эта теорема позволяет преобразовать отношение расстояний
точки d s до точек dt и В самом деле, достаточно предположить,
что точка d4 находится в бесконечности. Прямая Z) 4 проходит
при этом через точку О; итак, отношение равниол асложному
отношению прямых Ds, аО

197 Преобразование метрических свойств

211. Теорема. Если через точку а, взятую в плоскости данной

окружности, провести к окружности две секущие aMN и
aMrNr

(«черт. 194) и соединить попарно точки пересечения М, N,
Mr, N’ этих секущих с окружностью, то полученные прямые пе*)
Как и в предыдущих примерах, доказательство не будет полным, если
мы не убедимся, что надлежащим выбором точек а, £, с можно достичь
произвольного расположения точки О и прямых Л, В , С.

197 Новое определение поляры и её построение

ресекаются в двух точках Н и К> геометрическое место которых
есть поляра точки а, если секущие вращаются около этой точки.
Действительно, пусть Н—точка пересечения прямых ММ! и AW’,
К—точка пересечения прямых MNr и NM’.
Прямая НК пересекает хорды MN и MrNr в точках Р и Р гармонически
сопряжённых с точкой а относительно концов этих хорд
(п. 2 0 2 ). Следовательно, она будет полярой точки а.
Эта теорема даёт простой способ построения поляры точки относительно
окружности. Если точка лежит вне окружности, то она позволяет,
следовательно, пост-
Н роить с помощью одной линейки
касательные к окружности,
выходящие из этой точки.
Если обе секущие сливаются
в одну, то предыдущее геометрическое
место обращается
в геометрическое место точек
пересечения касательных к окружности
в концах хорды MN.
Но это геометрическое место
мы уже знаем (п. 205), так как
точка пересечения двух касательных
есть полюс прямой MN.

198 Новое определение поляры и её построение

212. В, С, D — четыре точки одной
окружности, то сложное отношение четырёх прямых, полученных
соединением этих точек с какой-либо точкой М окружности, не
зависит от положения точки М на кривой.
Действительно, если М и Мг— две точки окружности, то две
четвёрки (.MA, MB, МС, MD) и (MrА, М’В, М’С, М D) равны, так как
прямые, их составляющие, можно всегда рассматривать (п. 82) как
образующие между собой одни и те же углы с одним и тем же направлением
вращения.
П р и м е ч а н и е . Ничто не мешает принять за точку М одну из
данных точек, например А. Прямая МА заменяется при этом касательной
в точке А и предыдущее рассуждение остаётся в силе.
Постоянное сложное отношение, о котором была речь, называется
сложным отношением четырёх точек А, В, С, D, лежащих
на окружности. Если оно равно — 1, то говорят, что четыре соответствующие
точки, лежащие на окружности, — гармонические.
Следствие. Четыре данные касательные к одной окружности
определяют на подвижной касательной к той же окружности
четыре точки, имеющие постоянное сложное отношение.
Действительно, фигура, образованная четырьмя точками пересечения
неподвижных касательных с перемещающейся касательной,
имеет в качестве взаимно-полярной фигуры относительно данной
окружности четвёрку лучей (MA, MB, МС, MD) предыдущей теоремы.

198 Сложное отношение точек, лежащих на окружности

Сложным отношением четырёх касательных к одной окружности
называется сложное отношение четырёх точек пересечения этих
касательных с какой-либо подвижной касательной. Из нашего рассуждения
следует, что сложное отношение четырёх касательных равно
сложному отношению их точек касания.

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Приложение к сопряжённым хордам.

Две хорды, сопряжённые
относительно окружности, делят эту
окружность гармонически.
Пусть АВ и CD (черт. 195) — две такие
хорды, что CD проходит через полюс Р хорды
АВ. Прямые АР, АВ, ЛС, AD образуют
гармонический пучок, так как они делят гармонически
секущую PCD.
Но сложное отношение этих прямых равно
сложному отношению точек Л, В, С, D окружности,
так как прямая АР касается окружности
в точке Л. Черт. 195.

Следствие. Четыре касательные, проведённые
к окружности через две сопряжённые точки, делят любую
касательную гармонически.
Теоремы, обратные двум последним теоремам, также справедливы.
Их доказательство мы предоставляем читателю.

УПРАЖНЕНИЯ.
237. Две точки Л и В сопряжены относительно окружности О . Доказать, что
1°. окружности, имеющие своими центрами точки А и В и ортогональные
к окружности О, ортогональны между собой;
2°. окружность, построенная на отрезке А В как на диаметре, пересекает
ортогонально окружность О.
Найти зависимость, существующую между тремя сторонами треугольника
О А В и радиусом R окружности.
238. Найти, пользуясь предыдущим упражнением, геометрическое место
точек, поляры которых относительно трёх данных окружностей пересекаются
в одной точке, и геометрическое место точек пересечения этих поляр.
239. Если провести в вершинах вписанного в окружность четырёхугольника
касательные к этой окружности так, чтобы получился описанный
четырёхугольник, то
1°. диагонали обоих четырёхугольников проходят через одну и ту же
точку и образуют гармоническую четвёрку;
2°. третьи диагонали соответствующих полных четырёхсторонников лежат
на одной и той же прямой и делят друг друга гармонически.
240. Через две точки прямой D проведены к окружности касательные.
Таким образом, получается полный четырёхсторонник, одной из диагоналей
которого служит сама прямая D . Доказать, что две другие диагонали проходят
через полюс прямой D .
241. Даны две окружности О и О’ и их предельные точки (упр. 152) Р
и Q ; доказать, что
1°. полярой каждой из предельных точек относительно той и другой
окружности будет одна и та же прямая, проходящая через другую предельную
точку;
2°. не существует других точек (на конечном расстоянии), которые имели
бы одну и ту же поляру относительно обеих окружностей;

198 Сложное отношение точек, лежащих на окружности

3°. перпендикуляр к линии центров, проведённый через точку пересечения
внутренней общей касательной и внешней общей касательной, проходит
через одну из точек Р или Q (доказать, что этот перпендикуляр имеет
один и тот же полюс относительно обеих окружностей);
4°. прямая, которая соединяет между собой точки касания одной из
окружностей с внешней общей касательной и с внутренней общей касательной,
проходит через одну из точек Р или Q .

199 Приложение к сопряжённым хордам

Видео:ЧТО ТАКОЕ ПОЛЮСА ЗЕМЛИ ?Скачать

Что собой представляет полярный круг? А что за кругом?

Многим полярный круг представляется как какая-то далекая граница, за которой находятся вечно снежные суровые края, где всегда лютуют морозы, дуют сильные ветра. Что же собой представляет этот «круг», и как он выглядит?

Видео:Всё обо всём Экватор ЗемлиСкачать

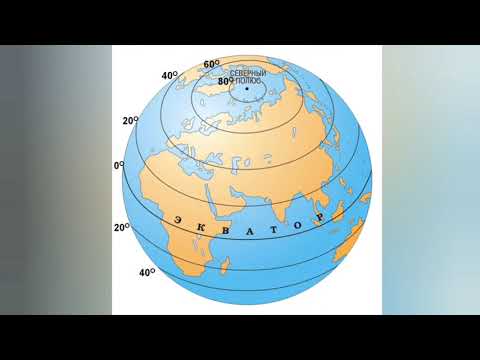
Что такое полярный круг?

Это воображаемые линии на поверхности Земли, лежащие на широте 66’33» к северу и к югу от экватора — условная граница, за которой можно наблюдать такие природные явления, как полярные день и ночь. Там ночь длится от 1 суток на широте самих кругов (Северного и Южного) до 176 — собственно на полюсах (Северном и Южном).

Полярный день — это такое время, когда солнце не уходит за горизонт. При этом чем ближе территория к полюсу, тем длиннее этот период. На широте самой границы он длится 24 часа, а на полюсе — 189 суток. К примеру, на широте г. Мурманска ночь может длиться 40 суток, а день — 61.

В Северном полушарии, на широте самого полярного круга, такой день начинается с июня, с 22 числа. Подобное явление параллельно происходит и в Южном полушарии, но в другое полугодии.

Видео:Определение географических координат 5 класс.Скачать

Как движется Земля? Немного о распределении света и тепла

Движение Земли происходит по орбите вокруг Солнца. Кроме этого, она вращается и вокруг своей оси, которая находится под наклоном к плоскости орбиты движения. Когда Земля расположена на одной стороне этой орбиты, Северное полушарие освещается солнечными лучами больше, чем Южное.

Таким образом, в это время в Северном и Южном полушарии, соответственно, лето и зима. А в обратном случае (Земля на другой стороне орбиты), наоборот — зима и лето.

Солнце отдает энергию всем процессам, которые происходят на планете Земля. Естественно, когда солнце располагается высоко над горизонтом, свет падает почти вертикально на поверхность планеты и, конечно, сильнее нагревает ее. При расположении солнца низко над горизонтом лучи только скользят по поверхности земли, слабее нагревая ее. Поэтому существует разделение на тепловые пояса.

Большую часть света и тепла получают территории, расположенные по обе стороны от экватора. Почти круглый год солнце здесь постоянно расположено высоко над горизонтом, при этом сильно прогревает сушу и океан. Эта часть земли называется тропическим поясом, потому что она располагается между тропиками (Северным и Южным).

У полюсов Земли, наоборот, весь год холодно. Даже в летнее время здесь солнце расположено довольно низко над горизонтом. Эти районы называются Северным и Южным полярными поясами Земли. Между тропическими и полярными поясами находятся умеренные, которые соответственно ограничены Северным и Южным тропиками и теми самыми полярными кругами.

Видео:§2 Различные уравнения окружностиСкачать

Полярный круг Северного полушария Земли

Северный, как и Южный круг — это одна из 5 главных географических параллелей, обозначенных на географической карте планеты. Северный полярный круг, широта которого 66°33’44», расположен в северной стороне от экватора. А область, расположенная к северу от этого круга, — Арктика. Южнее от него расположен пояс умеренного климата (северный).

Сам Северный полярный круг представляет собой южную границу той территории, где бывают полярные дни.

Немного людей живет на территориях в тех местах в связи с суровым климатом и исключительно тяжелыми условиями.

И все же Северный полярный круг России имеет на своей территории три крупных города с немалым количеством населения: Мурманск, Норильск и Воркута. Также здесь находится 4-й по количеству жителей город Тромсё (Норвегия).

Видео:Загадки Севера. Северный полюсСкачать

География Северного полярного круга

В Аляске, на обочине шоссе Далтон, есть знак, обозначающий размещение данного полярного круга по планете. Он простирается через океан (Северный Ледовитый), Скандинавский полуостров, Северную Азию, Северную Америку и Гренландию.

По суше эта условная граница проходит через территории восьми стран: Норвегию, Швецию, Финляндию, Россию, США (Аляску), Канаду, Данию (Гренландию) и Исландию.

Полярный круг России представляет за своей чертой территории Заполярья (вышеперечисленные города).

Видео:Физика - движение по окружностиСкачать

Южное полушарие Земли

Полярный круг, широта которого составляет 66°33’44» в южную сторону от экватора, является параллелью, аналогичной северному, расположенному в противоположном полушарии планеты. Это тоже одна из пяти географических главных параллелей географической карты Земли.

Видео:Полярные координатыСкачать

Антарктида и Арктика, особенности

Эти географические зоны имеют некоторые отличия:

• Антарктида — континент, омываемый со всех сторон водами морей и океанов.
• Арктика — океан, который находится под вечными ледниками, окруженный со всех сторон землей.
• Впервые люди высадились на берег Антарктиды лишь двести лет тому назад, она никогда не была заселена людьми.
• На территории Арктики люди проживают уже около четырех столетий.
• В Антарктиде обитают многочисленные животные (огромное количество полярных птиц, моржей, белых медведей и овцебыков), а в Арктике — большое количество птиц и морских млекопитающих (большие колонии пингвинов, альбатросов, морских котиков).
• В Арктику лучше совершать путешествие с июня по сентябрь, а в Антарктиду — с октября по март.
• В любое время года в полярных областях можно увидеть обилие снега и величавые айсберги самых удивительных форм.

Жителям Заполярья приходится в декабре-январе обходиться без солнечного света, а летом (в июне) можно и не включать освещение в домах.

Полярное солнце довольно слабо греет. В связи с этим и лето в этих краях холодное и очень короткое.

📹 Видео

ИНТЕРЕСНЫЕ ФАКТЫ ПРО СЕВЕРНЫЙ И ЮЖНЫЙ ПОЛЮСАСкачать

Физика - Магнитное полеСкачать

Особые точки ФКП.Порядок полюсаСкачать

Полярная система координат.Скачать

Поляры | Олимпиадная математикаСкачать

Почему над Антарктидой не летают Самолеты?Скачать

Построение кривой в полярной системе координатСкачать

Почему Никому не Разрешено Проводить Исследования в Антарктике?Скачать

Почему нам запрещено посещать АнтарктидуСкачать

Киножурнал - Хочу всё знать (2 серия) - О Северном Полюсе, играх и электричествеСкачать