Чертежный треугольник и транспортир (7 видео)

Измерение углов. Транспортир. Виды углов

Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения (1 мм, 1 см, 1 м и т.д.). Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения — с градусом, записывают так 1 ° .

Градусная мера угла — это число, которое показывает, сколько раз градус и его части укладываются в данном угле.

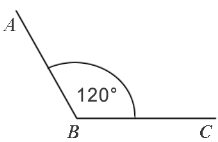
Пример:

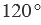
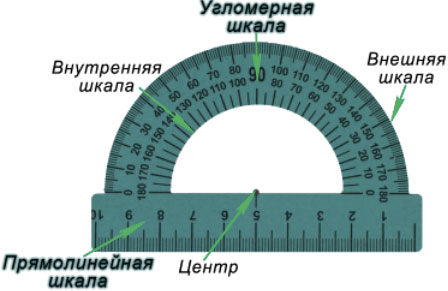
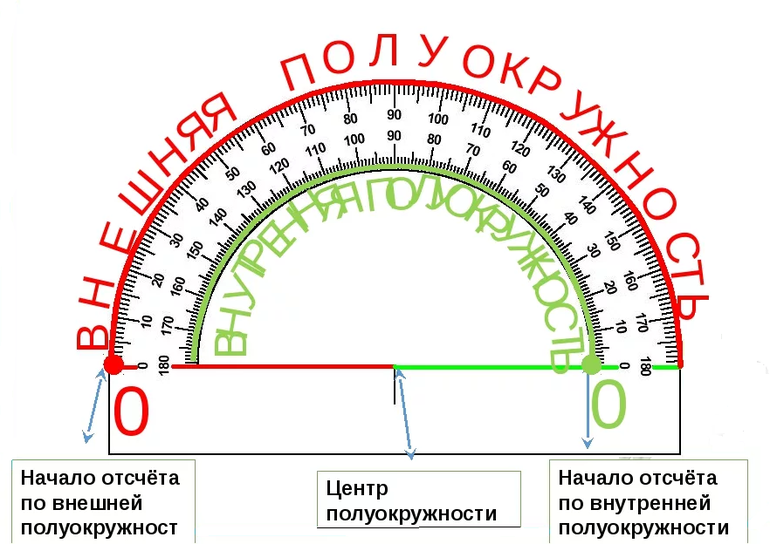
Градусная мера угла ABC равна . Говорят: «Угол ABC равен 120 градусам». Пишут: .

Транспортир — это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .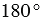

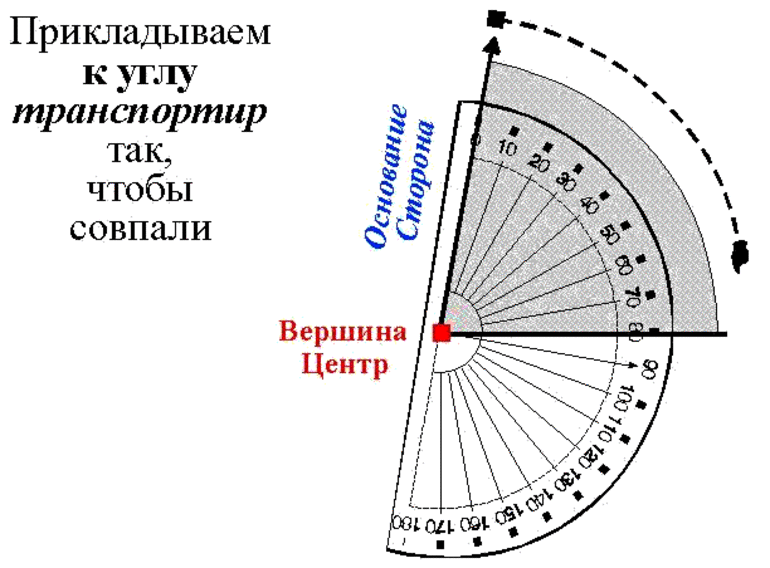
Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.

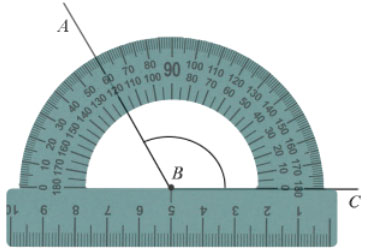
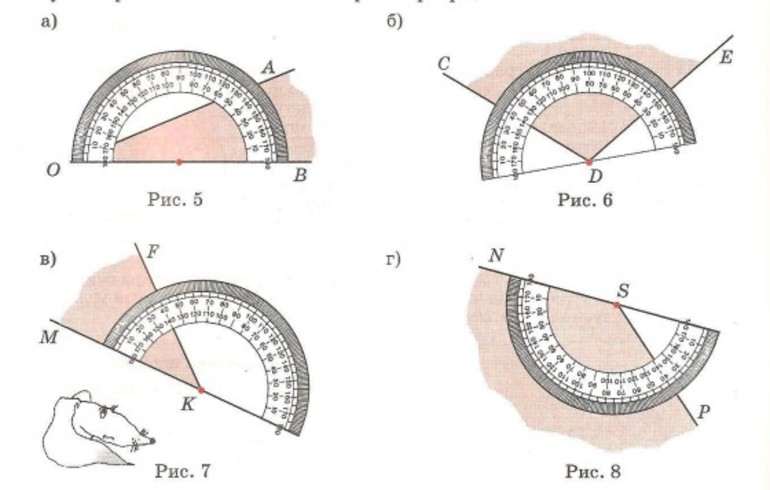
Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).

Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .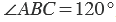

Содержание

Свойства:
Виды углов:
Транспортир — как правильно пользоваться инструментом для построения и измерения углов?
История изобретения
Разновидности и использование
Измерение градусов угла
Построение угла
Измерение углов
💥 Видео

Свойства:

Равные углы имеют равные градусные меры.
Меньший угол имеетменьшую градусную меру.
Развернутый угол равен.
Неразвернутый угол меньше.
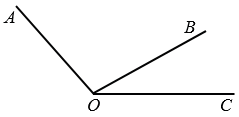
Если лучделит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов, т.е. на рисунке ниже

АОС = АОВ + ВОС.

Виды углов:

Острый угол — угол, градусная мера которого меньше 90 ° .

Прямой угол — угол, градусная мера которого равна 90 ° .

Тупой угол — угол, градусная мера которого больше 90 °, но меньше 180 ° .

Биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90 0 .

АОС — развернутый, ОВ — биссектриса, АОВ = ВОС = 90 0 .

Поделись с друзьями в социальных сетях:

Видео:Измерение угла с помощью транспортираСкачать

Транспортир — как правильно пользоваться инструментом для построения и измерения углов?

Люди обычно сталкиваются с транспортирами в математике, когда учатся в школе создавать точные геометрические фигуры. Возможно, у многих из них никогда больше не будет причин снова использовать эти приборы, тем не менее транспортиры имеют долгую историю применения в различных областях.

Видео:Сравнение углов. Виды углов. Чертежный треугольник. 5 класс.Скачать

История изобретения

Происхождение этого математического инструмента восходит к жрецам в Египте и Вавилоне, которые установили меру углов в градусах, минутах и секундах. Однако до времён классической Греции тригонометрия не использовалась в математике.

Во втором веке до нашей эры астроном Гиппарх из Никии изобрёл тригонометрический стол, для измерения треугольников. Затем Птолемей включил в свою великую астрономическую книгу «Альмагест» таблицу, с угловыми приращениями от 0 до 180°, с погрешностью менее 1/3600 единиц. Он также объяснил метод составления этой таблицы, и на протяжении всей книги приводил много примеров того, как вычислять с помощью неё неизвестные элементы фигур.

Птолемей также был автором, так называемой теоремы Менелая для решения сферических треугольников, и на протяжении многих веков его тригонометрия была основным пособием для астрономов.

Возможно, в то же время, учёные Индии также разработали тригонометрическую систему, основанную на функции синуса, которая, в отличие от используемого в настоящее время синуса, была не пропорцией, а длиной стороны, противоположной углу в прямом треугольнике этой гипотенузы. Индийские математики использовали разные значения для этого в своих таблицах.

Томас Бландевиль рассказал о приборе специально созданном, для рисования и измерения фигур в своём «Кратком описании универсальных карт» 1589 года. Как видно из названия, он применял его, чтобы править навигационные карты для использования в высоких широтах.

Другие европейские математики также описывали подобные приборы примерно в то же время. Независимо от того, кто первым придумал этот инструмент, к началу XVII века он вошёл в стандартную практику мореплавателей и геодезистов. К XVIII веку транспортиры начали появляться в учебниках по геодезии и геометрии.

Транспортиры в современном понимании возникли во второй половине XVIII века, когда такие учёные, как Джесси Рамсден и Георг Фридрих Брандер, усовершенствовали ранее созданные устройства.

В то время предпочтительными материалами для их изготовления были:

В первой половине XX века начали применять олово и целлулоид.

Называться транспортиром (рус.) прибор стал в 1610 году. Термин произошёл от средневекового слова protractor, что означает «переносить», который, в свою очередь, произошел от латинского слова protrahere «тянуть вперёд».

Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Разновидности и использование

Транспортир — это простой гониометр для измерения или создания угла. Он выглядит как круглый или полукруглый диск с делением. Диск может быть изготовлен из пластика, прочной бумаги или листового металла. Типичными являются диаметры от 8 до 15 см и деления на 1° и 0,5°, при измерении также 0,5 Гон (новый градус). Точность составляет от 0,1 до 0,5° в зависимости от диаметра шкалы. Более точные приборы имеют поворотную рейку со шкалой (длина до миллиметра).

Частично из-за различного использования их изготавливают во многих формах: знакомый полукруг, а также круги, прямоугольники, квадраты или четверть круга (квадранты). Они также могут иметь различные диаметры. Их изготавливают из латуни, стали, дерева, слоновой кости или пластика. Самой распространённой формой является полукруг с ограничительной шкалой в 180 градусов.

Угловой транспортир — градуированный круглый инструмент с одной поворотной рукой; используется для измерения или разметки. В строительстве часто требуется отмерить угол в 90 градусов. Иногда прилагается шкала Вернье, чтобы дать более точные показания. Прибор широко применяется для изготовления архитектурных и механических чертежей, хотя его использование уменьшилось с появлением современного программного обеспечения для рисования.

Универсальные транспортиры скоса используются изготовителями инструментов; поскольку они делают измерения посредством механического контакта с предметом, то классифицируются как механические транспортиры.

Угловой транспортир применяется для того, чтобы измерить и проверить углы с очень жёсткими допусками. Он считывает до 5 угловых минут (5 или 1/12°) и может измерять от 0 до 360°.

Сегодня также применяются электронные приборы, которые обычно работают с поворотным датчиком. Кроме того, связанными с транспортиром приборами являются:

теодолит;
оптический транспортир в строительной промышленности и геодезии;
инклинометр для определения уклонов и косвенной альтиметрии;
секстант для навигации.

Видео:Построение угла с помощью транспортираСкачать

Измерение градусов угла

Для того чтобы научиться пользоваться транспортиром инструкция нужна на начальном этапе. Для его освоения достаточно нескольких минут и примеров (смотреть онлайн) того, как можно измерить и построить угол с помощью этого прибора.

Измерить угол, значит найти его величину. Углы разделяют на три типа: острый, тупой и прямой. Прямоугольный имеет 90 градусов. Все углы что имеют больше этого значения называются тупыми, и соответственно меньше 90 градусов называются острыми. Развёрнутый угол имеет 180 градусов.

Понимание того, что углы являются частями окружностей, полезно, потому что тогда конструкция транспортира обретает смысл. Поскольку полный круг имеет 360º, отдельный угол должен быть меньше этого числа, потому что он часть круга.

Алгоритм измерения следующий: для того чтобы измерить угол транспортиром необходимо приложить его центр верхней кромки линейки к вершине измеряемого угла. Вершина — это точка, в которой две из трёх сторон треугольника пересекаются.

Нижнюю планку (основание) транспортира нужно выставить горизонтально. Каждый транспортир имеет точку, спроектированную в центре основания, Эта средняя точка располагается на вершине угла, который должен быть измерен или нанесён на график. Другая сторона должна пересекать транспортир в одной из точек его дуги.

Если вторая сторона (линия) до дуги не доходит нужно продолжить её с помощью простой или масштабной линейки. То число, на шкале дуги, которое будет пересечено линией и есть величина угла в градусах.

Для удобства на большинстве транспортиров сделано две шкалы, внутренняя и внешняя, которые отображают числа в каждой строке.

Видео:Построение угла с помощью транспортира. 5 клСкачать

Построение угла

Берётся чистый лист бумаги в клетку. На нём карандашом отмечается точка, от которой проводиться прямая линия, как одна из сторон будущего угла. Эта черта служит для того, чтобы задать направление второй стороне. В простых упражнениях, для приобретения навыка построения угла, линия проводится горизонтально.

Центр основы транспортира располагается на любом из концов черты, который будет вершиной угла. Эта точка отмечается на бумаге карандашом. И именно к этому месту, внутри отверстия и присоединяется вершина угла, одна из сторон которого должна совпадать в горизонтальной плоскости с внутренней стороной линейки транспортира.

Затем на шкале отмечается необходимый градус. С внутренней стороны отверстия также обозначается точка возле этого градуса. И от вершины проводится прямая линия к этой точке. Таким образом, получается необходимый угол.

Для того чтобы правильно пользоваться транспортиром очень важно его выровнять, и точно прикладывать, для получения верных измерений.

Пересечённые линии в верхней части прямой кромки линейки должны совпадать с вершиной (конечной точкой), где соединяются два луча.

Видео:КАК ИЗМЕРИТЬ УГЛЫ ТРЕУГОЛЬНИКА ТРАНСПОРТИРОМ? Примеры | МАТЕМАТИКА 5 классСкачать

Измерение углов

Андрей Андреев, Полина Ачева, Алексей Панов
«Квантик» №12, 2020

В школьной геометрии угол — это фигура, состоящая из двух лучей, выходящих из одной точки (рис. 1). Эта точка называется вершиной угла, а лучи — его сторонами. Угол разбивает плоскость на две части: на рисунке 2 они окрашены в зелёный и жёлтый цвет. Эти части называются плоскими углами.

Измерить угол можно обычным транспортиром, который размечен в градусах от 0° до 180° (рис. 3, слева).

Рис. 2 (слева). Два плоских угла — зелёный и жёлтый. Рис. 3. Транспортиры — полукруговой и круговой

Плоские углы удобно измерять круговым транспортиром, размеченным от 0° до 360° (рис. 3, справа). Конечно, для научных и технических измерений углов нужны более точные приборы: например, такие, как на рисунке 4. Слева там изображён один из астрономических инструментов Тихо Браге, с которым он проводил свои высокоточные наблюдения. Результаты этих наблюдений позволили Кеплеру вывести законы движения планет. Справа — современный электронный теодолит, используемый в геодезии.

Рис. 4. Секстант Тихо Браге и современный теодолит

А можно ли измерять углы, не применяя вообще никаких инструментов?

«Ручное измерение» углов. Об этом методе мы прочли в книге «Музыка сфер. Математика и астрономия», написанной Розой Марией Рос. Цитируем:

. Существует очень простой, хотя и не слишком точный, способ измерения углов вручную. Если мы вытянем руку перед собой, то растопыренная ладонь будет указывать интервал в 20°, кулак — 10°, большой палец — 2°, мизинец — 1°. Этот способ могут использовать и взрослые, и дети, так как размеры ладони человека увеличиваются пропорционально длине его руки.

Поясним сказанное. Пусть мы наблюдаем за двумя звёздами, расположенными на небе недалеко друг от друга. Направление взгляда на каждую из них задаёт луч. Угол между этими двумя лучами (с вершиной в глазу наблюдателя) мы и хотим измерить. Его величина называется угловым расстоянием между звёздами. Вытянем правую руку с растопыренной ладонью, как на рисунке 5 справа. Если кончик большого пальца закрывает одну звезду, а кончик мизинца — другую, угловое расстояние между звёздами можно оценить в 20°. Прикладывая ладони друг к другу, можно измерять углы до 40° (рис. 5, справа внизу).

Рис. 5. Ручное измерение углов

Задача 1. Звёздной ночью найдите на небе ковш Большой Медведицы (рис. 6) и «вручную» оцените угловое расстояние между звёздами Мерак и Дубхе.

Рис. 6. Ковш Большой Медведицы

Напомним: в направлении Мерак → Дубхе расположена Полярная звезда, указывающая путь на север.

Задача 2. Отыщите на небе Полярную звезду и найдите угловое расстояние между ней и звездой Дубхе.

Решив задачи, вы сможете проверить себя, так как известно, что расстояние Дубхе — Полярная звезда примерно в 5 раз больше расстояния Мерак — Дубхе.

Конечно, ручное измерение углов не позволяет добиться хорошей точности. Сейчас мы опишем бесприборный метод измерения углов, позволяющий проводить измерения со сколь угодно высокой точностью. Начнём с нескольких экспериментов.

Рис. 7. Треугольник

Эксперименты с треугольниками: «60°» ≠ 60°. Мы купили несколько одинаковых треугольников, как на рисунке 7. Углы этого треугольника по стандарту должны быть равны 30°, 60° и 90°, но мы хотим проверить, так ли это на самом деле. Начнём со среднего по величине из этих углов, обозначив его α. Итак, верно ли, что α = 60°?

Рис. 8. Каждый треугольник получается из соседнего поворотом на угол α, см. видео

Эксперимент № 1: поворачиваем треугольники. Выложим на плоскость один за другим шесть треугольников, как на рисунке 8: каждый получен из соседнего поворотом на угол α.

Видно, что первый и последний треугольники не сомкнулись, и это означает, что в сумме шесть одинаковых углов α дают меньше 360°, то есть 6α 360°, откуда α > 360°/7. Объединим полученные два неравенства и запишем их в виде

Эксперимент № 2: переворачиваем треугольники. На рисунке 9 представлен другой способ выкладывания треугольников. Каждый треугольник получается из соседнего переворотом вокруг их общей стороны на 180°. Этот способ даёт такую же оценку измеряемого угла, но он будет удобнее для нас в дальнейшем.

Практический совет: чтобы треугольники не смещались при малейшем прикосновении, не укладывайте их на скользкую поверхность. На видео мы воспользовались оборотной стороной коврика для ванной: она сделана из материала, не скользящего даже по влажному гладкому полу ванной комнаты, и идеально подходит для наших экспериментов.

Уменьшаем число треугольников, увеличиваем точность измерения. Первое усовершенствование: будем использовать единственный экземпляр треугольника. Опять обозначим один из его углов через α. Нарисуем на плоскости луч и совместим вершину угла с вершиной луча, а одну из сторон угла направим вдоль луча, как на рисунке 7. Перевернём треугольник вокруг другой стороны угла (не лежащей на луче). Потом перевернём треугольник вокруг другой стороны угла, опять перевернём и т. д., пока максимально не приблизимся к нарисованному лучу. Так мы определим максимальное k, для которого kα 360°, то есть

Задача 3. На рисунке 10 представлен угол α . Увеличьте рисунок и по этому шаблону из тонкого жёсткого листа пластика вырежьте соответствующий плоский угол. Используя разобранный нами метод измерения, с помощью переворотов оцените величину этого угла. Тут вас ждёт небольшой сюрприз. Угол на рисунке подобран специальным образом. Существует такое небольшое число n, что величина α укладывается в n · 360° целое число раз. Так что с помощью нашего метода вы сможете определить это n и найти точное значение угла α.

Задача 4 (Г. Фельдман, Д. Баранов, XXXI Турнир городов). Нарисован угол, и ещё имеется только циркуль.

Какое наименьшее число окружностей надо провести, чтобы наверняка определить, является ли данный угол острым?
Как определить, равен ли данный угол 31° (разрешается проводить сколько угодно окружностей)?

В пункте б можно обойтись и без циркуля, если есть деревянный угольник с данным углом, о котором мы хотим выяснить, равен ли он 31°.

И напоследок — небольшой список увлекательных книг, в которых обсуждается измерение углов в астрономии и геометрии, с небольшими аннотациями.

Роза Мария Рос. Музыка сфер. Астрономия и математика (М.: Де Агостини, 2014). В этой замечательной книге рассказывается о планетах и звёздах, об измерении углов, космических расстояний и времени.
Александр Шень. Космография (М.: МЦНМО, 2019). В книге разбираются основные вопросы космографии: как движутся звёзды по небу, отчего бывают зима и лето, почему Луна видна в форме серпа, когда и как происходят затмения. Прочитав её, вы поймёте, что астрономия не может обойтись без измерения углов.
Яков Перельман. Занимательная геометрия на вольном воздухе и дома, 7-е изд. (М.-Л.: ГИТТЛ, 1950). Обязательно обратите внимание на эту книгу. В третьей главе разобрано много задач на измерение углов подручными средствами и подробно рассказано о простейших устройствах для измерения углов, в том числе о посохе Якова и о грабельном угломере.
Особо рекомендуем раздел «Определение величины данного угла без всяких измерений» (с. 138–140), где описан метод измерения углов, «предложенный в 1946 г. З. Рупейка из Каунаса». По-видимому, этот раздел был добавлен редактором седьмого издания книги Б. А. Кордемским. Сам Яков Перельман скончался в 1942 году в блокадном Ленинграде.
Александр Шень. Геометрия в задачах (М.: МЦНМО, 2017). Второй раздел этой книги как раз называется «Измерение углов». Там много интересных задач, над которыми стоит подумать. Среди них мы выделим задачу № 38.