Биссектриса прямоугольного треугольника 7 класс

Базовым понятием и одним из наиболее интересных и полезных объектов школьной математики является биссектриса. С её помощью доказываются многие положения планиметрии, упрощается решение задач.

Известные свойства позволяют рассматривать геометрические фигуры с разных точек зрения. Появляется вариативность при выборе пути доказательств.

Становится возможным использование инструмента алгебры, например, свойство пропорции, нахождение неизвестных величин, решение алгебраических уравнений при рассмотрении геометрических вопросов.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Что такое биссектриса в геометрии

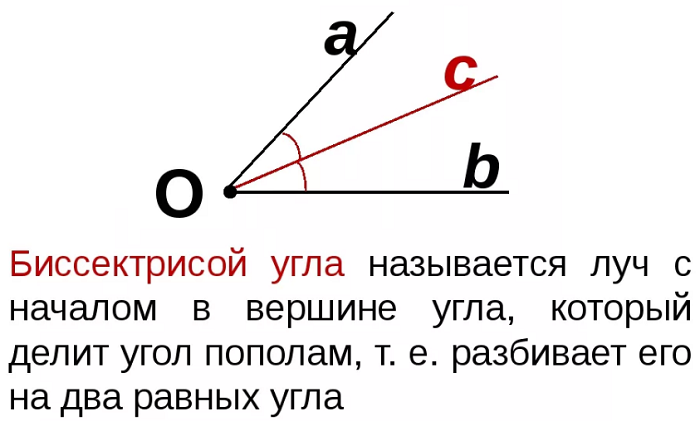
Рассматривают луч, выходящий из вершины угла или его часть (отрезок), который делит угол пополам. Такой луч (или, соответственно, отрезок) называется биссектрисой.

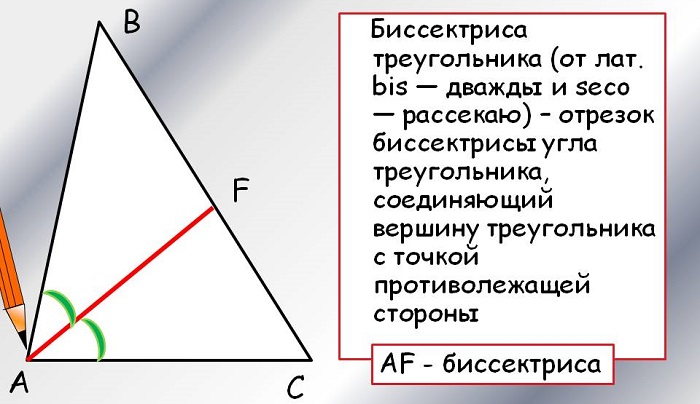
Часто для треугольников определение немного сужают, говоря об отрезке, соединяющем вершину угла, делящем его пополам, с точкой на противолежащей стороне. При этом рассматривается внутренняя область фигуры.

В то же время, часто при решении задач используются прямые, делящие внешние углы на два равных.

Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Биссектриса прямоугольного треугольника

Для прямоугольного треугольника одна из биссектрис образует равные углы, величины которых хорошо просчитываются (45 градусов).

Это помогает вычислять углы при решении задач, связанных с фигурами, которые можно представить в виде прямоугольных треугольников или прямоугольников.

В тупоугольном треугольнике биссектриса делит больший угол на равные части, величина которых меньше 90 0 .

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Свойства биссектрисы треугольника

1. Каждая точка этой линии равноудалена от сторон угла. Часто эту характеристику выбирают в качестве определения, поскольку верно и обратное утверждение для любого произвольного треугольника. Это позволяет находить и радиус вписанной окружности.

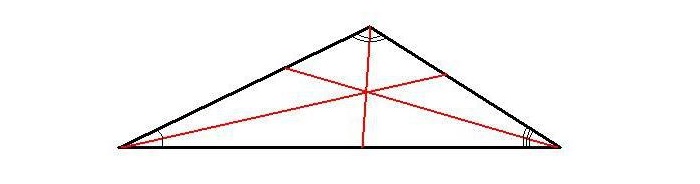
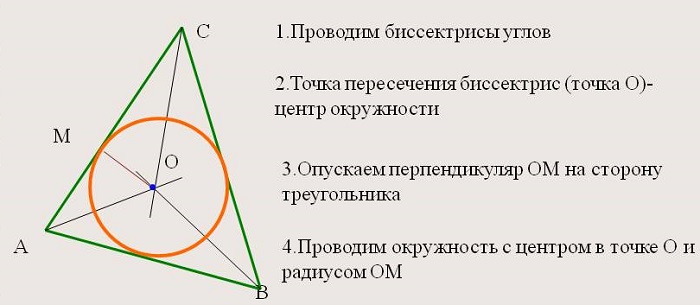
2. Все внутренние отрезки, делящие углы пополам, пересекаются в одной точке, которая является центром окружности, вписанной в фигуру, т. е. точка пересечения находится на равных расстояниях от сторон.

Данное свойство позволяет решать целый класс разнообразных задач, выводить формулы для радиусов вписанных окружностей правильных многоугольников.

Благодаря этому утверждению, легко доказывается следующее правило:

Площадь описанного многоугольника равна:

где p – полупериметр, а r – радиус вписанной окружности.

Это позволяет находить решение не только планиметрических, но и стереометрических задач.

Важную роль играют внешние биссектрисы треугольника. Вместе с внутренними они образуют прямые углы;

3. Сумма величин двух прилежащих сторон, делённая на длину противолежащей стороны, задаёт отношение частей биссектрисы (считая от вершины), полученных точкой пересечения всех трёх соответствующих линий.

Некоторые виды геометрических фигур, в силу своих особенностей, порождают особые примечательные характеристики;

4. В равнобедренном треугольнике биссектриса, проведённая к основанию, одновременно является медианой и высотой. Две другие – равны между собой.

В этом случае основание параллельно внешней биссектрисе.

Обратное положение также имеет место. Если прямая проведена параллельно основанию равнобедренного треугольника через некоторую вершину, то внешняя биссектриса при этой вершине является частью этой линии;

5. Для равностороннего многоугольника важной характеристикой считается равенство всех биссектрис;

6. У правильного треугольника все внешние биссектрисы параллельны сторонам;

7. Выделяют несколько особенностей, среди которых есть следующая теорема:

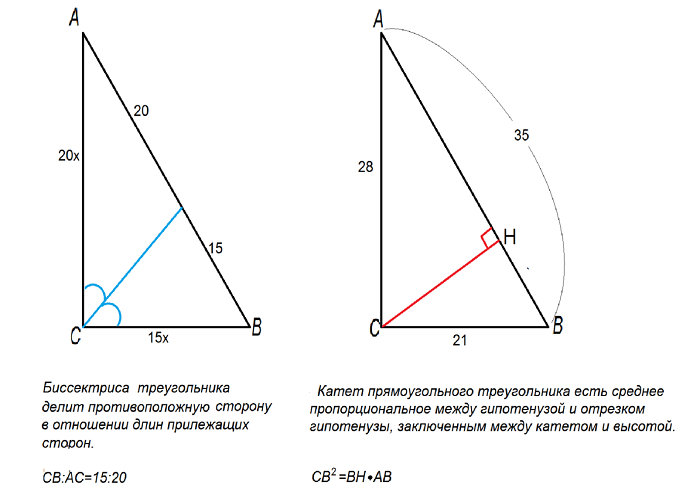
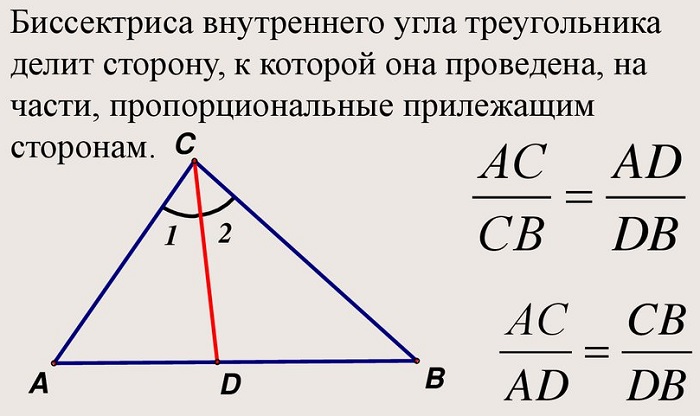
«Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам».

Обратное утверждение («Прямая делит сторону на отрезки, пропорциональные двум другим сторонам») выражает признаки того, что рассматриваемая линия является внутренней биссектрисой;

8. Разносторонний треугольник позволяет определить взаимное расположение его высоты, медианы и биссектрисы, проведённых из одной точки. В частности, медиана и высота располагаются по разные стороны от третьей линии.

Видео:ГЕОМЕТРИЯ 7 класс : Решение задач по теме "Равнобедренный треугольник"Скачать

Все формулы биссектрисы в треугольнике

В зависимости от исходных данных, длина биссектрисы, проведённой к стороне C, l_c, равна:

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Примеры решения задач

Задача №1

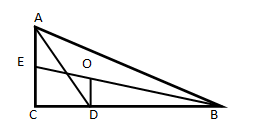
В ΔABC ∠C = 90°, проведена биссектриса острого угла. Отрезок, соединяющий её основание с точкой пересечения медиан, перпендикулярен катету. Найти углы заданной фигуры.

Пусть ∠ACB = 90°, AD – биссектриса, BE – медиана, O – точка пересечения медиан, OD⊥BC.

Тогда OE : OB = 1 : 2по свойству медиан.

Так как OD⊥BC, то ODIIOC, следовательно, ΔBOD ∼ ΔBEC по второму признаку подобия, поэтому, по свойству подобных фигур, CD : DB = 1 : 2.

Это означает, что CA : AB = 1 : 2.

Так как катет равен половине гипотенузы, то ∠ABC = 30°, откуда ∠CAB = 60°.

Задача №2

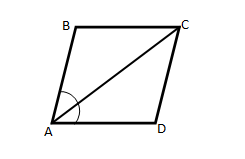
Диагональ параллелограмма делит его острый угол пополам. Доказать, что этот параллелограмм является ромбом.

Так как ABCD – параллелограмм, то ∠DAC = ∠ACB, как накрест лежащие при параллельных прямых AD, BC и секущей AC.

По условию, ∠DAC = ∠ACB = ∠BAC, поэтому ΔACB равнобедренный, то есть AB = BC, следовательно, ABCD – ромб.

Видео:Свойства прямоугольного треугольника. Практическая часть. 7 класс.Скачать

Свойства биссектрисы прямоугольного треугольника

В данной публикации мы рассмотрим основные свойства биссектрисы прямоугольного треугольника, проведенной из прямого и острого углов, а также разберем примеры решения задач по данной теме.

Примечание: напомним, что прямоугольным называется треугольник, в котором один из углов прямой (т.е. равен 90°), а два остальных – острые ( Содержание скрыть

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Свойства биссектрисы прямоугольного треугольника

Свойство 1

Если в прямоугольном треугольнике известны катеты, то длину биссектрисы, проведенной из прямого угла к гипотенузе, можно вычислить по формуле:

Свойство 2

Длину биссектрисы в прямоугольном треугольнике, проведенную из острого угла к противолежащему катету, можно вычислить по формуле:

• l_a – биссектриса к катету;
• α – острый угол, из которого проведена биссектриса.

Также можно использовать другую формулу, если известны все три стороны треугольника:

Примечания:

• Прямоугольный треугольник может быть равнобедренным, и в этом случае к нему, в т.ч., применимы свойства биссектрисы равнобедренного треугольника.
• Общие свойства биссектрисы в любом треугольнике представлены в нашей публикации – “Определение и свойства биссектрисы угла треугольника”.

Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Примеры задач

Задача 1
Найдите длину биссектрисы, которая проведена к гипотенузе прямоугольного треугольника, если известно, что его катеты равны 21 и 28 см.

Решение
Воспользуемся формулой, приведенной в Свойстве 1, подставив в нее известные значения:

Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Вычислите длину биссектрисы, проведенной к катету с наименьшей длиной.

Решение
Пример катеты за “a” (9 см) и “b” (12 см).

Для начала найдем гипотенузу треугольника (c), воспользовавшись теоремой Пифагора, согласно которой квадрат гипотенузы равняется сумме квадратов катетов:
c 2 = a 2 + b 2 = 9 2 + 12 2 = 225.
Следовательно, c = 15 см.

Теперь мы можем применить формулу, рассмотренную в Свойстве 2 для нахождения длины биссектрисы:

Видео:КАК СТАТЬ ОТЛИЧНИКОМ // Как Хорошо Учиться? // Советы для школыСкачать

Свойства биссектрис треугольника (Геометрия 7 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Видео:Построение биссектрисы угла. 7 класс.Скачать

Свойства биссектрис треугольника

Свойство 1

Биссектрисы треугольника пересекаются в одной точке — центре вписанной в треугольник окружности.

Свойство 2

Если CD — биссектриса угла C ? ABC, то

Свойство 3

Точка пересечения биссектрис делит биссектрису угла С в отношении a + bc , считая от вершины:

Свойство 4

Биссектриса угла C вычисляется по формулам:

Признак равенства прямоугольных треугольников по двум катетам

Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.

Признак равенства прямоугольных треугольников по катету и гипотенузе

Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.

Признак равенства по гипотенузе и острому углу

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Признак равенства прямоугольных треугольников по катету и острому углу

Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Видео:Свойство биссектрисы треугольника с доказательствомСкачать

Свойства серединного перпендикуляра

Рассмотрим свойства серединного перпендикуляра. Начнем со свойства серединного перпендикуляра к отрезку.

I) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

II) И обратно: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

I)

AB- отрезок, C — середина AB,

m — серединный перпендикуляр к AB,

1. Если точка M совпадает с точкой C.

Так как AC=BC по условию, то и AM=BM.

2. Если точка M не совпадает с точкой C.

Рассмотрим треугольники ACM и BCM

то есть треугольники ACM и BCM — прямоугольные.

AC=BC (по условию), CM — общий катет.

Из равенства треугольников следует равенство соответствующих сторон: AM=BM.

Что и требовалось доказать.

II) Дано: AB — отрезок, C — середина AB,

m — серединный перпендикуляр к AB,

Так как AK=BK (по условию), то треугольник AKB — равнобедренный с основанием AB (по определению ). Так как C — середина AB, то KC — медиана треугольника AKB.

По свойству равнобедренного треугольника медиана, проведенная к основанию, является также его высотой, то есть

Что и требовалось доказать.

Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 991 человек из 78 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 672 человека из 74 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 307 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Построение биссектрисы в треугольникеСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 546 250 материалов в базе

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 21.09.2018
• 376
• 1

• 21.09.2018
• 1048
• 23

• 21.09.2018
• 381
• 1

• 21.09.2018
• 228
• 0

• 21.09.2018
• 345
• 0

• 21.09.2018
• 939
• 6

• 21.09.2018
• 239
• 0

• 21.09.2018
• 173
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 22.09.2018 2264
• DOCX 150 кбайт
• 6 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Шаронова Селена Михайловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 2 месяца
• Подписчики: 0
• Всего просмотров: 436531
• Всего материалов: 175

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Минобрнауки подготовит государственный рейтинг университетов

Время чтения: 1 минута

В Омской области школы и колледжи перейдут на дистанционное обучение с 7 по 21 февраля

Время чтения: 1 минута

В «Единой России» предложили ввести раздел безопасности детей в интернете в курс ОБЖ

Время чтения: 3 минуты

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

В Госдуме предложили ввести пост уполномоченного по правам учителей

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🎥 Видео

биссектриса прямоугольного треугольника #SHORTSСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать

ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.Скачать

7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать