Через вершину c прямого угла треугольника abc проведена плоскость параллельная гипотенузе ab

2. Через вершину прямого угла С равнобедренного прямоугольного треугольника АСВ проведена плоскость а, параллельная гипотенузе и составляющая с катетом угол 30°. Найдите угол между плоскостью АВС и плоскостью а.

ответ

См. чертеж. М — середина АВ.
Плоскость альфа — это плоскость СВ1А1. Прямая В1А1 — проекция (. ) прямой АВ на «альфа». Прямая, проходящая через С и ппраллельная АВ и А1В1 — это ребро двугранного угла между плоскостями АВС и «альфа».
По условию, угол АСА1 = 30 градусов. Это означает, что расстояние между прямой АВ и плоскостью «альфа» равно АС*sin(30) = AC/2; То есть ММ1 = АС/2.
МС = АС/корень(2)
поэтому sin(M1CM) = M1M/MC = (AC/2)/(АС/корень(2)) = корень(2)/2
Значит угол М1СМ = 45 градусам.

Ясно, что оба отрезка перпендикулярны ребру двугранного угла, так как в равнобедренных треугольниках (АВС и А1В1С) они являются медианами к основанию, а значит, высотами, основания же параллельны ребру. Это я так, для ясности добавил :)))

https://znanija.com/task/463491

Задача№1.
Через вершину прямого угла С равнобедренного прямоугольного треугольника АВС проведена плоскость альфа параллельная гипотенузе и составляющая с катетом угол 30 градусов. Найдите угол между плоскостью АВС и плоскостью альфа.

Из вершины прямого угла С опустим перпендикуляр СМ на гипотенузу АВ. Восстановим перпендикуляры в точках А и М к плоскости АВС. Эти перпендикуляры пересекут плоскость альфа в точках А1 и М1 соответственно. Обозначим длину этих перпендикуляров буквой h, а длину катета треугольника АВС буквой а. Тогда из треугольника АВС находим: СМ = a/ √2. Из треугольника САА1 определяем h = a/ √3. Наконец, из треугольника СММ1 найдём тангенс угла MСM1 — угла между плоскостью АВС и плоскостью альфа
tg(СММ1) = √2/3.

Видео:№155. Через вершину прямого угла С равнобедренного прямоугольного треугольника ABCСкачать

2. Через вершину прямого угла С равнобедренного прямоугольного треугольника. Геометрия Зив Б.Г. 10 класс. Самостоятельная работа 11. Вариант 4

2. Через вершину прямого угла С равнобедренного прямоугольного треугольника АСВ проведена плоскость а, параллельная гипотенузе и составляющая с катетом угол 30°. Найдите угол между плоскостью АВС и плоскостью а.

ответ

См. чертеж. М — середина АВ.
Плоскость альфа — это плоскость СВ1А1. Прямая В1А1 — проекция (. ) прямой АВ на «альфа». Прямая, проходящая через С и ппраллельная АВ и А1В1 — это ребро двугранного угла между плоскостями АВС и «альфа».
По условию, угол АСА1 = 30 градусов. Это означает, что расстояние между прямой АВ и плоскостью «альфа» равно АС*sin(30) = AC/2; То есть ММ1 = АС/2.
МС = АС/корень(2)
поэтому sin(M1CM) = M1M/MC = (AC/2)/(АС/корень(2)) = корень(2)/2
Значит угол М1СМ = 45 градусам.

Ясно, что оба отрезка перпендикулярны ребру двугранного угла, так как в равнобедренных треугольниках (АВС и А1В1С) они являются медианами к основанию, а значит, высотами, основания же параллельны ребру. Это я так, для ясности добавил :)))

https://znanija.com/task/463491

Задача№1.
Через вершину прямого угла С равнобедренного прямоугольного треугольника АВС проведена плоскость альфа параллельная гипотенузе и составляющая с катетом угол 30 градусов. Найдите угол между плоскостью АВС и плоскостью альфа.

Из вершины прямого угла С опустим перпендикуляр СМ на гипотенузу АВ. Восстановим перпендикуляры в точках А и М к плоскости АВС. Эти перпендикуляры пересекут плоскость альфа в точках А1 и М1 соответственно. Обозначим длину этих перпендикуляров буквой h, а длину катета треугольника АВС буквой а. Тогда из треугольника АВС находим: СМ = a/ √2. Из треугольника САА1 определяем h = a/ √3. Наконец, из треугольника СММ1 найдём тангенс угла MСM1 — угла между плоскостью АВС и плоскостью альфа
tg(СММ1) = √2/3.

Видео:№205. Через вершину С прямого угла прямоугольного треугольника ABC проведена прямая CD, перпендикуляСкачать

Через вершину прямого угла С равнобедренного прямоугольного треугольника ABC проведена плоскость а, параллельная гипотенузе и составляющая с катетом угол 30°?

Математика | 5 — 9 классы

Через вершину прямого угла С равнобедренного прямоугольного треугольника ABC проведена плоскость а, параллельная гипотенузе и составляющая с катетом угол 30°.

Найдите угол между плоскостью ABC и плоскостью а.

Из вершины прямого угла С опустим перпендикуляр СМ на гипотенузу АВ.

Восстановим перпендикуляры в точках А и М к плоскости АВС.

Эти перпендикуляры пересекут плоскость альфа в точках А1 и М1 соответственно.

Обозначим длину этих перпендикуляров буквой h, а длину катета треугольника АВС буквой а.

Тогда из треугольника АВС находим : СМ = a / √2.

Из треугольника САА1 определяем h = a / √3.

Наконец, из треугольника СММ1 найдём тангенс угла MСM1 — угла между плоскостью АВС и плоскостью альфа

Видео:№145. Через вершину А прямоугольного треугольника ABC с прямым углом С проведена прямая AD,Скачать

Основанием пирамиды DABC является прямоугольный треугольник ABC с прямым углом C ?

Основанием пирамиды DABC является прямоугольный треугольник ABC с прямым углом C .

Катет AC равен 2.

Боковое ребро DC, перпендикулярное плоскости основания, равно 1.

Чему равен (в градусах) угол наклона боковой грани к плоскости основания?

Видео:№473. Через вершину С треугольника ABC проведена прямая m, параллельная стороне АВ. Докажите,Скачать

Помогите, умоляю?

Через вершину острого угла прямоугольного треугольника проведена плоскость, параллельная одному из катетов.

Проекция другого катета на эту плоскость равна 3 см, а проекция гипотенузы на эту плоскость равна 6 см.

Найти длину катета параллельного к плоскости.

С рисунком пожалуйста.

Видео:Геометрия Через вершину прямого угла B прямоугольного треугольника ABC к его плоскости проведенСкачать

Дан треугольник ABC со сторонами : AВ = 9 ; ВС = 6 и АС = 5?

Дан треугольник ABC со сторонами : AВ = 9 ; ВС = 6 и АС = 5.

Через сторону АС проходит плоскость М, составляющая с плоскостью треугольника угол в 45°.

Найти расстояние между плоскостью М и вершиной В.

Видео:№243. Через вершину С треугольника ABC проведена прямая, параллельная его биссектрисе АА1Скачать

К плоскости прямоугольного треугольника ABC (угол С = 90°) восстановлен перпендикуляр АК?

К плоскости прямоугольного треугольника ABC (угол С = 90°) восстановлен перпендикуляр АК.

Укажите прямые, перпендикулярные друг другу.

Видео:Геометрия Через вершину угла C треугольника ABC к его плоскости проведен перпендикуляр CNСкачать

Катеты прямоугольного треугольника АВС равны 3см?

Катеты прямоугольного треугольника АВС равны 3см.

Из вершины прямого угла С проведен к плоскости этого треугольника перпендикуляр СД = 1см.

Найти расстояние от точки Д до гипотенузы АВ.

Видео:№150. Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная к плоскостиСкачать

Треугольник abc — прямоугольный и равнобедренный с прямым углом c и гипотенузой 4 см?

Треугольник abc — прямоугольный и равнобедренный с прямым углом c и гипотенузой 4 см.

Отрезок cm перпендикулярен плоскости треугольника и равен 2 см.

Найдите расстояние от точки m до прямой ab.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Гипотенуза прямоугольного треугольника принадлежит плоскости b, а вершина прямого угла этой плоскости не принадлежит?

Гипотенуза прямоугольного треугольника принадлежит плоскости b, а вершина прямого угла этой плоскости не принадлежит.

Проведена из вершины прямого угла делит гипотенузу на отрезки длиной 2, 25 см и 4 см, а угол между плоскостью треугольника и плоскостью b равен 30.

Найти угол который образует больший катет с плоскостью b.

Видео:№130. Через вершину В квадрата ABCD проведена прямая ВМ. Известно, что ∠MBA = ∠MBC=90°, МВ =m, АВСкачать

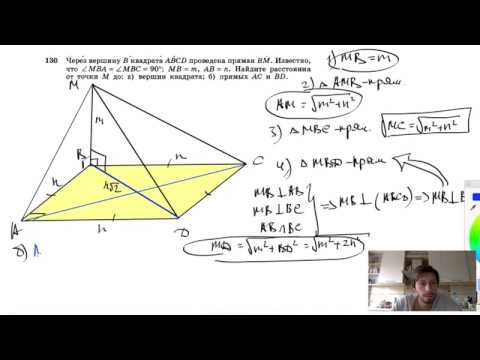
Дан прямоугольный треугольник abc : (угол с = 90)?

Дан прямоугольный треугольник abc : (угол с = 90).

Прямая bd перпендикулярна плоскости abc.

, точка k принадлежит cd.

Найдите угол между прямыми ac и bk.

Видео:Геометрия В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину ВСкачать

Основанием пирамиды DABCявляется правильный треугольник ABC сторона которого равна p?

Основанием пирамиды DABCявляется правильный треугольник ABC сторона которого равна p.

Ребро DA перпендикулярно к плоскости ABC, а плоскость DBC составляет с плоскостью ABC угол 30°.

Найдите площадь боковой и площадь полной поверхности пирамиды.

Видео:№158. Через вершину В ромба ABCD проведена прямая ВМ, перпендикулярная к его плоскости. НайдитеСкачать

К плоскости треугольника abc (угол c = 90°) через середину гипотенузы проведен перпендикуляр OM?

К плоскости треугольника abc (угол c = 90°) через середину гипотенузы проведен перпендикуляр OM.

Из точки М опустите перпендикуляры на катеты треугольника.

На этой странице сайта вы найдете ответы на вопрос Через вершину прямого угла С равнобедренного прямоугольного треугольника ABC проведена плоскость а, параллельная гипотенузе и составляющая с катетом угол 30°?, относящийся к категории Математика. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

📽️ Видео

№152. Через вершину В квадрата ABCD проведена прямая BF, перпендикулярная к его плоскости. НайдитеСкачать

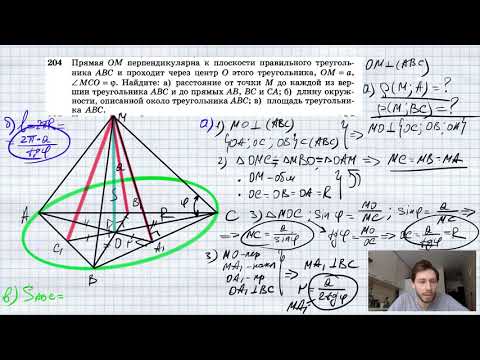
№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать

№121. В треугольнике ABC дано: ∠C = 90°, AC = 6 см, ВС = 8 см, СМ — медиана. Через вершину ССкачать

№172. Катет АС прямоугольного треугольника ABC с прямым углом С лежит в плоскости α, а уголСкачать

№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

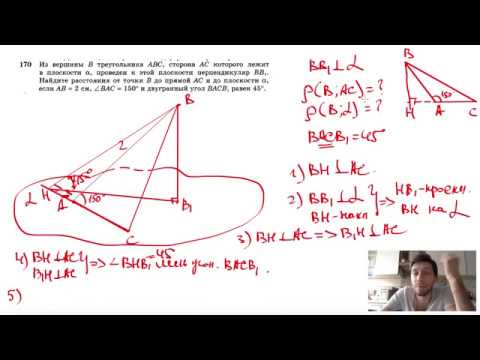
№170. Из вершины В треугольника ABC, сторона АС которого лежит в плоскости а, проведен к этойСкачать

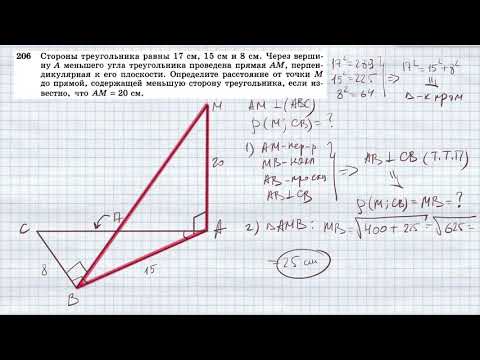
№206. Стороны треугольника равны 17 см, 15 см и 8 см. Через вершину A меньшего угла треугольника проСкачать

ЕГЭ 2023 Ященко 8 вариант ФИПИ школе полный разбор!Скачать