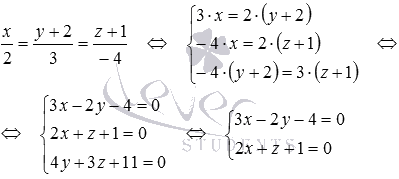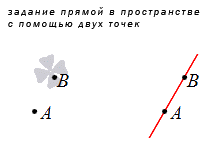Эта статья является развернутым ответом на вопрос: «Как составить уравнение прямой, проходящей через заданную точку плоскости параллельно заданной прямой»? Сначала приведена необходимая теория, после чего разобраны решения характерных задач. В заключении разобрано нахождение уравнений прямой, проходящей через заданную точку трехмерного пространства параллельно заданной прямой.
Навигация по странице.
- Уравнение прямой, проходящей через заданную точку плоскости параллельно заданной прямой.
- Уравнения прямой, проходящей через заданную точку пространства параллельно заданной прямой.
- Прямая в пространстве – необходимые сведения
- Прямая в пространстве – понятие
- Взаимное расположение прямых в пространстве
- Способы задания прямой в пространстве
- Параллельные прямые в пространстве. Параллельность трех прямых
- 🌟 Видео
Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Уравнение прямой, проходящей через заданную точку плоскости параллельно заданной прямой.
Чтобы составление уравнения прямой, проходящей через заданную точку плоскости параллельно заданной прямой, не вызвало затруднений, вспомним важные факты.
Аксиома параллельных прямых гласит: на плоскости через точку, не лежащую на заданной прямой, проходит единственная прямая, параллельная данной. Таким образом, мы можем определить конкретную прямую a на плоскости, указав прямую линию b , которой параллельна прямая a , и точку М1 , не лежащую на прямой b , через которую проходит прямая a .
Поставим перед собой следующую задачу.
Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy . Пусть в этой системе координат задана точка 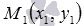
Решим поставленную задачу.
Из условия мы знаем координаты точки М1 , через которую проходит прямая a . Этих данных не достаточно, чтобы написать уравнение прямой a .
Нам еще нужно знать
Как же их найти?
По условию прямая a параллельна прямой b , тогда, на основании необходимого и достаточного условия параллельности двух прямых на плоскости, в качестве направляющего вектора прямой a мы можем принять направляющий вектор прямой b , в качестве нормального вектора прямой a мы можем взять нормальный вектор прямой b , а угловой коэффициент прямой a равен угловому коэффициенту прямой b (или они оба бесконечны).
Таким образом, чтобы в прямоугольной системе координат на плоскости написать уравнение прямой a , проходящей через заданную точку 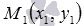
- или координаты направляющего вектора прямой b (
),
- или координаты нормального вектора прямой b (
),
- или угловой коэффициент прямой b (
),
принять их соответственно в качестве
- координат направляющего вектора прямой a (
),
- координат нормального вектора прямой a (
),
- углового коэффициента прямой a (
),
и записать требуемое уравнение прямой a соответственно в виде
или
,
,
.
Внесем ясности – приведем примеры с подробными решениями на каждый случай.
Напишите уравнение прямой, которая в прямоугольной системе координат Oxy на плоскости проходит через точку 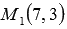
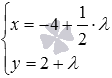
Из параметрических уравнений прямой 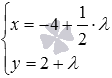
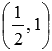
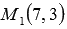
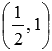
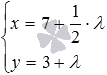
Это и есть искомые уравнения прямой, проходящей через заданную точку 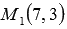
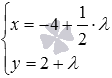
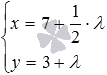
Иногда требуется составить уравнение прямой определенного вида, проходящей через заданную точку плоскости параллельно заданной прямой. В этом случае сначала записываем уравнение прямой, которое проще всего получить, после чего приводим его к нужному виду.
Составьте уравнение прямой в отрезках, если эта прямая в прямоугольной системе координат Oxy проходит через точку плоскости с координатами 
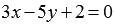
Очевидно, нормальным вектором прямой, общее уравнение которой имеет вид 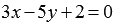
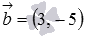

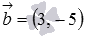
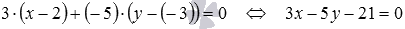

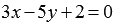
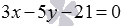
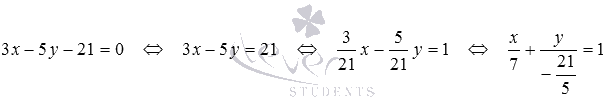
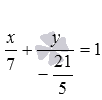
Напишите уравнение прямой, которая в прямоугольной системе координат Oxy на плоскости проходит через точку 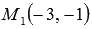
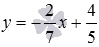
Мы знаем, что угловые коэффициенты параллельных прямых равны (или бесконечны), тогда 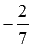
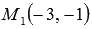
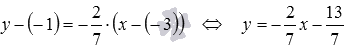
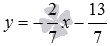
Итак, уравнение прямой a , проходящей через заданную точку плоскости M1 параллельно заданной прямой b , проще всего записывать в таком виде, в котором записано уравнение заданной прямой b .
Видео:12. Уравнения прямой в пространстве Решение задачСкачать

Уравнения прямой, проходящей через заданную точку пространства параллельно заданной прямой.
В трехмерном пространстве через точку М1 , не лежащую на прямой b , проходит единственная прямая a , параллельная прямой b . Таким образом, прямую в пространстве можно задать, указав точку, через которую она проходит, и прямую, которой она параллельна.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , задана прямая b некоторыми уравнениями прямой в пространстве и точка 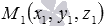
Направляющим вектором прямой a является направляющий вектор прямой b . Таким образом, по известным уравнениям прямой b мы можем определить координаты ее направляющего вектора, а, следовательно, и координаты направляющего вектора прямой a . После этого мы можем записать канонические уравнения прямой a в пространстве и параметрические уравнения прямой a в пространстве, так как известны координаты точки, лежащей на прямой a , и координаты направляющего вектора прямой a .
Рассмотрим решения примеров.
Напишите уравнения прямой, которая проходит через начало прямоугольной системы координат Oxyz в трехмерном пространстве параллельно прямой 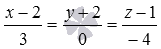
Очевидно, направляющим вектором прямой 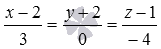
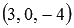
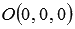
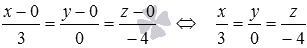
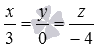
От канонических уравнений прямой a при необходимости можно будет перейти к уравнениям двух плоскостей, пересекающихся по прямой a .
В трехмерном пространстве в прямоугольной системе координат Oxyz заданы три точки 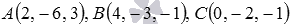
Направляющим вектором прямой, проходящей через точку С параллельно прямой АВ , является вектор 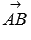
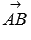
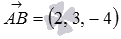
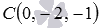
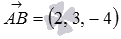
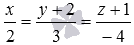
Осталось получить уравнения двух пересекающихся плоскостей, задающих эту прямую:
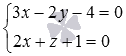
Видео:10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Прямая в пространстве – необходимые сведения
Статья рассказывает о взаимном расположении линий в пространстве. Будут рассмотрены основные способы задания прямой с приведением примеров и наглядных рисунков.
Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Прямая в пространстве – понятие
Раздел о прямой на плоскости дает представление о течки и прямой. Расположение прямой в пространстве аналогично. Если мысленно отметить две точки и провести линию, соединив их, получим прямую, уходящую в бесконечность.
Точки, прямые и отрезки в пространстве обозначаются аналогично расположению в плоскости.
Если прямая располагается на плоскости в пространстве, тогда это можно подкрепить аксиомами:
- через две точки можно провести единственную прямую;
- если две точки прямой лежат в плоскости, то все остальные точки, расположенные на прямой принадлежат плоскости.
Имеет место аксиома, благодаря которой можно рассматривать прямую в пространстве в качестве двух пересеченных плоскостей:
Если две плоскости имеют общую точку, тогда имеют общую прямую, на которой лежат все общие точки этих плоскостей. Показано на рисунке, приведенном ниже.
Видео:Уравнение параллельной прямойСкачать

Взаимное расположение прямых в пространстве
Прямые в пространстве могут совпадать, в таком случае они будут иметь большое количество общих точек или хотя бы 2 .
Две прямые, расположенные в пространстве, могут пересекаться в случае наличия одной общей точки.
Данный случай говорит о том, что прямые располагаются на плоскости трехмерного пространства. Когда прямые, расположенные в пространстве, пересекаются, то переходим к определению угла между пересекающимися прямыми.
Две прямые пространства параллельны в том случае, если расположены в одной плоскости без общих точек.
Рассмотрим ниже расположение параллельных прямых.
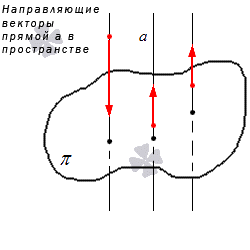
После рассмотрения определения параллельных прямых, расположенных в пространстве, необходимо добавить о направляющих векторах прямой.
Ненулевой вектор, который располагается на прямой или на параллельной ему прямой, называют направляющим вектором данной прямой.
Если по условию дана линия в пространстве, то он используется для решения задач.
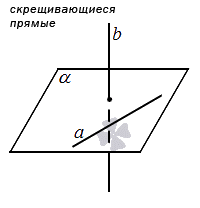
Две прямые пространства могут быть скрещивающимися.
Две прямые называют скрещивающимися, при условии, что они лежат в одной плоскости.
Это тесно связано с определением угла между скрещивающимися прямыми.
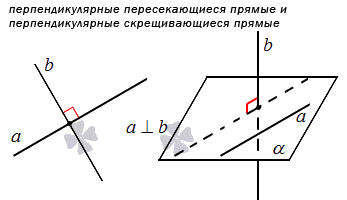
Особым случаем считается пересечение или скрещивание прямых под прямым углом в пространстве. Их называют перпендикулярными. Рассмотрим на рисунке.
Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Способы задания прямой в пространстве
Для того, чтобы расположить прямую в пространстве, существует несколько методов.
Из аксиомы для двух точек плоскости имеем, что через них может быть задана единственная прямая. При расположении двух точек в пространстве также задается только одна прямая, проходящая через них.
При прямоугольной системе координат прямая задается с помощью координат точек, которые располагаются в трехмерном пространстве. Это и позволяет составить уравнение прямой, проходящей через две заданные точки.
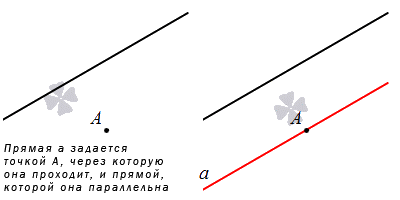
Еще один способ задания прямой – это теорема. Через любую точку пространства, не лежащую на данной прямой, может проходить прямая, параллельная данной, причем только одна.
Отсюда следует, что при задавании прямой и точки, не лежащей на ней, сможем определить прямую, которая параллельна заданной и проходит через указанную точку.
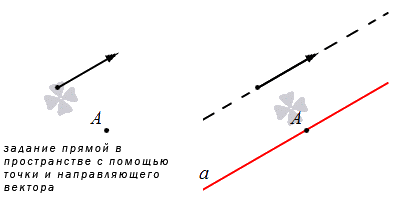
Есть способ, когда можно указать точку, направляющий вектор и прямую, которая проходит через нее. При задании прямой относительно прямоугольной систему координат, можно говорить о канонических и параметрических уравнениях прямой в пространстве.
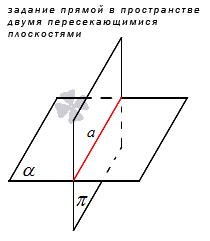
Немаловажный способ задания прямой – это способ, основанный на аксиоме: если две плоскости имеют общую точку, тогда имеют общую прямую, где располагаются общие точки заданных плоскостей. При задании двух пересекающихся плоскостей можно определить прямую пространства.
Если задана плоскость и нележащая в ней точка, тогда существует прямая, проходящая через нее и перпендикулярная заданной плоскости, причем только одна. Этот способ задания базируется на теореме. Получаем, что для определения прямой достаточно задать плоскость, перпендикулярную ей, с точкой, через которую проходит заданная прямая.
В случае, если прямая задается относительно введенной прямоугольной системы координат, то следует укрепить знания из статьиуравнения прямой, проходящей через заданную точку перпендикулярно в заданной плоскости.Рассмотрим задание прямой, используя точку, через которую она пройдет, и плоскости, которая располагается перпендикулярно относительно заданной прямой.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Параллельные прямые в пространстве. Параллельность трех прямых
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы дадим основные определения и теоремы на тему параллельных прямых в пространстве.
В начале урока рассмотрим определение параллельных прямых в пространстве и докажем теорему о том, что через любую точку пространства можно провести только одну прямую, параллельную данной. Далее докажем лемму о двух параллельных прямых, пересекающих плоскость. И с ее помощью докажем теорему о двух прямых, параллельных третьей прямой.
🌟 Видео
Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Видеоурок "Канонические уравнения прямой"Скачать

11. Прямая в пространстве и ее уравненияСкачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Построение прямой, параллельной даннойСкачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Параллельность прямых. 10 класс.Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Параллельные прямые циркулемСкачать

Написать канонические и параметрические уравнения прямой в пространствеСкачать

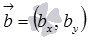 ),
),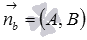 ),
),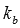 ),
),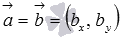 ),
),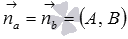 ),
),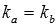 ),
),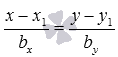 или
или 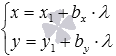 ,
,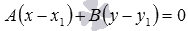 ,
,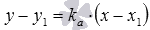 .
.