Через точку пересечения медиан треугольника проведена прямая параллельная одной из сторон

Геометрия | 5 — 9 классы

В треугольнике абс через точку пересечения медиан проведена прямая параллельная стороне ас и пересекающая стороны аб и бс в точка к и е соответственно найдите ас если ке = 12 см найдите площадь треугольника бке если площадь треугольника равна = 72 см.

Тр — кBKE итр — кABC подобны по равным углам.

(соответственныеуглы при пересечении параллельных прямых секущей).

В подобных тр — ках отношение площадей равно квадрату коэффицента подобия.

Отношение медиан — коэффиценту подобия.

КЕ проходит через точку Опересечения медиан.

Медиана ВР делится точкой О в отношении 2 : 1, т.

Е. ВО ОР = 2 1 значит ВО ВР = 2 3 — коэффицент подобия.

КЕ АС = 2 3 АС = 12 * 3 2 = 18см

Sbke Sabc = 4 9 Sbke = 4 * 72 9 = 32cm² BO BP является отношением медиан, тк ВО медиана ВКЕ(Медиана ВР делит тр — к АВС и ВКЕ на два треугольника, которые попарно подобны с коэф — м 2 3, из соотношения подобия следует КО = ОЕ).

Видео:№245. Через точку пересечения биссектрис ВВ1 и СС1 треугольника ABC проведена прямая, параллельнаяСкачать

Медианы треугольника ABC пересекаются в точке O?

Медианы треугольника ABC пересекаются в точке O.

Через точку O проведена прямая, параллельная стороне AC и пересекающая стороны AB и BC в точках E и F соответственно.

Найдите EF, если сторона AC = 15 см.

Видео:Точка пересечения медиан в треугольникеСкачать

Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС в точке Р?

Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС в точке Р.

Найдите отношение площади треугольника АВК и к площади КРСМ.

Видео:Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Помогите пожалуйста?

В треугольнике АВС через точку пересечения медиан проведена прямая, параллельная стороне АС и пересекающая стороны АВ и ВС в точках К и Е соответственно.

Найдите АС, если КЕ = 12 см.

Найдите площадь треугольника ВКЕ, если площадь треугольника АВС равна 72 см ^ 2 (желательно с рисунком).

Видео:Уравнения стороны треугольника и медианыСкачать

В треугольнике АВС через точку пересечения медиан проведена прямая, параллельная ВС, пересекающая стороны АС и АВ в точках К и D соответственно?

В треугольнике АВС через точку пересечения медиан проведена прямая, параллельная ВС, пересекающая стороны АС и АВ в точках К и D соответственно.

Найдите KD, если CB = 15 см.

Найдите отношение площадей треугольников АВС и ADK.

Видео:№74. Через точку пересечения медиан грани BCD тетраэдра ABCD проведена плоскостьСкачать

Медианы треугольника АВС пересекаются в точке О, через точку О проведена прямая параллельная АС и пересекающаяя стороны АВ и ВС в точке Е и F соответственно?

Медианы треугольника АВС пересекаются в точке О, через точку О проведена прямая параллельная АС и пересекающаяя стороны АВ и ВС в точке Е и F соответственно.

Найдите ЕF, если сторона АС = 15.

Видео:Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС вСкачать

Медианы треугольника ABC пересекаются в точке O?

Медианы треугольника ABC пересекаются в точке O.

Через точку O проведена прямая, параллельная стороне AC и пересекающая стороны AB и BC в точках E и F соответственно.

Найдите EF, если сторона AC = 15см.

Видео:№366. Докажите, что если М — точка пересечения медиан треугольника ABC, а О — произвольная точкаСкачать

Медианы треугольника МNK пересекаются в точке О?

Медианы треугольника МNK пересекаются в точке О.

Через точку О проведена прямая, параллельная стороне МК и пересекающая стороны МN и NК в точках А и В соответственно.

Найдите МК, Если длина отрезка АВ равна 12 см.

Видео:Точка пересечения медиан.Скачать

Медианы треугольника MNK пересекаются в точке О?

Медианы треугольника MNK пересекаются в точке О.

Через точку О проведена прямая, параллельная стороне МК и пересекающая стороны МN и NK в точках А и В соответственно.

Найдите МК, если длина отрезка АВ равна 12 см.

Видео:№563. Через точку М, взятую на медиане AD треугольника ABC, и вершину В проведена прямая,Скачать

Медианы треугольника АВС пересекаются в точке О?

Медианы треугольника АВС пересекаются в точке О.

Через точку О проведена прямая, параллельная стороне Ас и пересекающая стороны АВ и ВС в точках К и М соответственно.

Найдите КМ, если сторона АС = 30 см.

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Медианы треугольника АВС пересекаются в точке О?

Медианы треугольника АВС пересекаются в точке О.

Через точку О проведена прямая, параллельная стороне АС и пересекающая стороны АВ и ВС в точках E и F соответственно.

Найдите EF, если сторона АС = 15 см.

На этой странице вы найдете ответ на вопрос В треугольнике абс через точку пересечения медиан проведена прямая параллельная стороне ас и пересекающая стороны аб и бс в точка к и е соответственно найдите ас если ке = 12 см найдите площадь треуго?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

В треугольниках ОА = ОВ как радиусы одной окружности, и О1А = О1В как радиусы другой окружности, сторона ОО1 — общая, треугольники равны по трём сторонам.

В условии допущена ошибка.

1. Где па — мм S = высота проведённая на сторону * сторона, следовательно S = BE * AD, тока на твоём рисунке нифига не понятно по длинам сторон 2. Где треугольник S = высота * 1 / 2 * основание, авс равнобедренный тк оас равнобедренный, во = 5 тк эт..

П о л у ч а е т с я 60 и 120 г р а д у с о в.

KF = ON = 3 TK = KF ; FK + KT = FT = 3 + 3 = 6 ; KO = FN = 7 ; FN = NE ; FN + NE = FE ; 7 + 7 = 14 ; FE = TS = 14 ; TF = SE = 6.

∠AOE = ∠AOB — ∠EOB = 24°.

Исходя из свойств высоты, получаем, что угол АВС равен 30, а катет лежащий на против угла в 30 градусов, равен половине гипотенузы, в данном случае катет это наша высота, следовательно ВС = 3, 45 * 2 = 6, 9.

1)120 2)80 3)60 4)В — 70, С — 40 5)60 6)30 7)40 8) A — 50, C — 70 9)M и К = 50, N — 80 10)Е — 40, D — 60 11)A — 30, D — 90, B — 60 12)A и B — 45, D — 90, M — 90.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Через точку пересечения медиан треугольника проведена прямая параллельная одной из сторон

Две фигуры $$ F$$ и $$ ^<text>$$ называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между двумя точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры $$ F$$ и $$ ^<text>$$ подобны, то пишется $$ Fsim ^<text>$$Напомним, что в записи подобия треугольников $$ ∆ABC

Два треугольника подобны:

• 1) если два угла одного соответственно равны двум углам другого;
• 2) если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;
• 3) если три стороны одного треугольника пропорциональны трём сторонам другого.

Из признаков подобия следует утверждения, которые удобно использовать в решении задач:

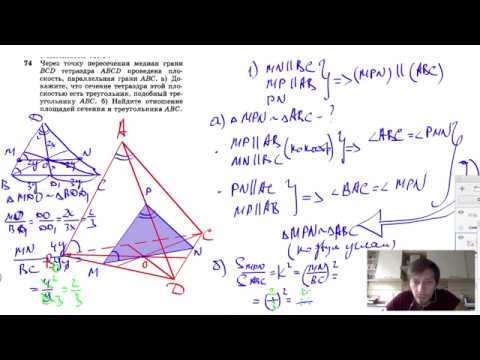
1°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие в различных точках, отсекает треугольник, подобный данному.

Рис. 5

2°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие стороны, отсекает на них отрезки, пропорциональные данным сторонам, т. е. если $$ MNleft|right|AC$$ (рис. 5), то

3°. Если прямая пересекает две стороны треугольника и отсекает на них пропорциональные отрезки, то она параллельна третьей стороне, т. е. если (см. рис. 5)

то $$ MN$$ параллельна $$ AC$$ (доказательство было дано в задании для 9 класса).

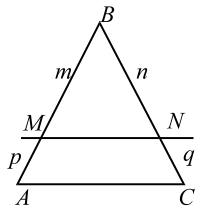
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках $$ M$$ и $$ N$$. Найти длину отрезка `MN`, если основания трапеции равны $$ a$$ и $$ b$$.

Пусть $$ O$$ точка пересечения диагоналей трапеции (рис. 6). Обозначим:

$$ AD=a, BC=b, MO=x, BO=p, OD=q.$$

$$1.;left.beginBCparallel AD\bigtriangleup BOCsimbigtriangleup DOA;(mathrm;mathrm;mathrm)endright|Rightarrowdfrac ba=dfrac pq$$ (1)

$$2.;left.beginMOparallel AD\bigtriangleup MBOsimbigtriangleup ABDendright|Rightarrowdfrac xa=dfrac p

$$. (2)

Результат этой задачи, как утверждение, верное для любой трапеции, следует запомнить.

Рис. 6

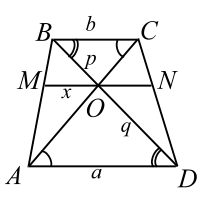
Из определения подобия фигур следует, что в подобных фигурах все соответствующие линейные элементы пропорциональны. Так, отношение периметров подобных треугольников равно отношению длин соответствующих сторон. Или, например, в подобных треугольниках отношение радиусов вписанных окружностей (также и описанных окружностей) равно отношению длин соответствующих сторон. Это замечание поможет нам решить следующую задачу.

Рис. 7

В прямоугольном треугольнике $$ ABC$$ из вершины $$ C$$ прямого угла проведена высота $$ CD$$ (рис. 7). Радиусы окружностей, вписанных в треугольники $$ ACD$$ и $$ BCD$$ равны соответственно $$ _$$ и $$ _$$. Найти радиус окружности, вписанной в треугольник $$ ABC$$.

Напомним, что площади подобных фигур относятся как квадраты соответствующих линейных элементов. Для треугольников это утверждение можно сформулировать так: площади подобных треугольников относятся как квадраты соответствующих сторон. Рассмотрим характерную задачу на эту тему.

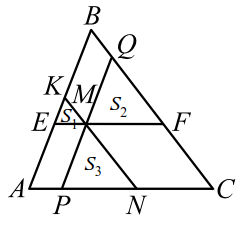Рис. 8

Через точку $$ M$$, лежащую внутри треугольника $$ ABC$$, проведены три прямые, параллельные его сторонам. При этом образовались три треугольника (рис. 8), площади которых равны $$ _$$, $$ _$$ и $$ _$$. Найти площадь треугольника $$ ABC$$.

Легко видеть, что треугольники $$ EKM$$, $$ MQF$$ и $$ PMN$$ подобны треугольнику $$ ABC$$.

Пусть $$ S$$ -площадь треугольника $$ ABC$$, тогда

А так как $$ EM=AP, MF=NC$$, то $$ EM+PN+MF=AP+PN+NC=AC$$.

Свойства медиан, высот, биссектрис треугольника

В наших заданиях 9-го и 10-го классов здесь повторяемые теоремы и утверждения были доказаны. Для некоторых из них мы напоминаем пути доказательств, доказывая их моменты и давая поясняющие рисунки.

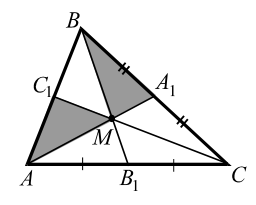Рис. 9

Теорема 1. Три медианы треугольника пересекаются в одной точке и точкой пересечения каждая медиана делится в отношении `2 : 1`, считая от вершины.

Теорема 2. Три медианы, пересекаясь, разбивают треугольник на `6` треугольников с общей вершиной, площади которых равны между собой.

(На рис. 9 площадь каждого из `6` треугольников с вершиной `M` и основанием, равным половине стороны, равна $$ <displaystyle frac>_$$. Точка пересечения медиан называется центром тяжести треугольника.

Теорема 3. Пусть $$ BD$$ — медиана треугольника

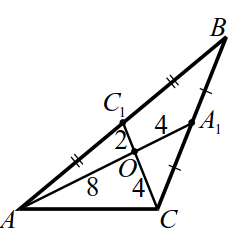Рис. 10

Расставим на рисунке 10 длины отрезков медиан. По условию, одна из сторон треугольника равна `12`, сторона $$ AC$$ не может равняться `12`, иначе $$ AC=AO+OC$$ — нарушено неравенство треугольника. Также не может равняться `12` сторона $$ AB$$, так в этом случае $$ A_=6$$ и треугольник $$ AO_$$ со сторонами `8`, `2`, `6` не существует. Значит, $$ BC=12$$ и $$ A_=6$$.

2. Площадь треугольника находим по формуле Герона:

По теореме 2 площадь треугольника $$ ABC$$ в `6` раз больше, находим $$ _=18sqrt$$.

Теорема 4. Три высоты треугольника или три прямые, на которых лежат высоты, пересекаются в одной точке. (Эта точка называется ортоцентром треугольника). В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.

Были доказаны также две леммы о высотах

1-ая лемма.

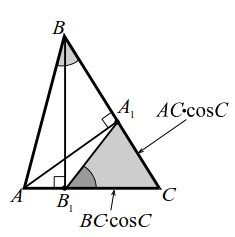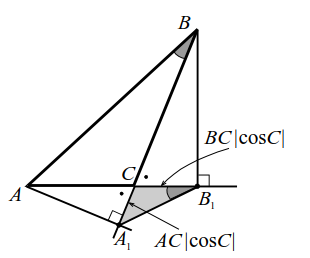Рис. 11a	Рис. 11б

2-ая лемма.

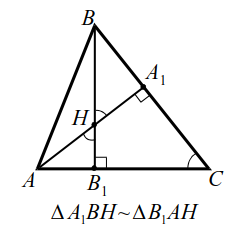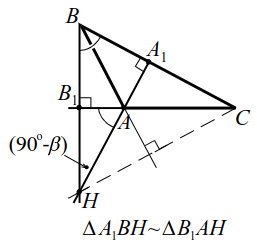Рис. 12a	Рис. 12б

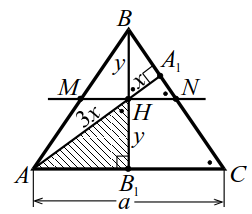Рис. 13

1. Точка $$ H$$ — середина высоты (рис. 13). Если отрезок $$ MH$$ проходит через точку $$ H$$ и параллелен основаниям, то `MN` — средняя линия; `MN=a/2`.

3. $$ angle _BC=90°-angle C$$, поэтому `ul(/_BHA_1=/_AHB_1=/_C)`, а по второй лемме о высотах $$ AH·H_=BH·H_$$ т. е. $$ 3^=^, y=xsqrt$$.

Теорема 5. Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если $$ AD$$ — биссектриса треугольника $$ ABC$$ (рис. 14), то

Доказательство легко выполните сами, применяя теорему синусов к треугольникам $$ ADB$$ и $$ ADC$$.

Теорема 6. Пусть $$ AD$$ — биссектриса треугольника $$ ABC$$ (рис. 14), тогда $$ AD=sqrt$$ (в обозначениях рисунка 14а)

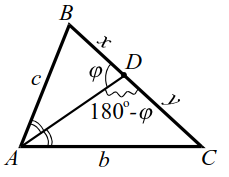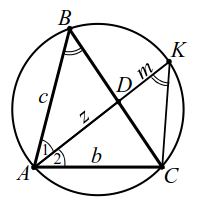Рис. 14	Рис. 14а

Эту теорему докажем. Опишем около треугольника $$ ABC$$ окружность, точку пересечения прямой $$ AD$$ и окружности обозначим $$ K$$ (рис. 14а).

По свойству пересекающихся хорд: $$ AD·DK=BD·CD$$, т. е. $$ z·m=x·y$$, тогда $$ ^=bc-xy$$, $$ z=sqrt$$.

В треугольнике $$ ABC$$ со сторонами $$ AB=5$$, $$ AC=3$$ биссектриса $$ AD=<displaystyle frac>$$. Найти сторону $$ BC$$ и радиус вписанной окружности.

Видео:№120. Через точку О пересечения диагоналей квадрата со стороной а проведена прямая ОКСкачать

Через точку пересечения медиан треугольника проведена прямая параллельная одной из сторон

Через точку пересечения медиан треугольника ABC параллельно прямой AB проведена прямая пересекающая стороны AC и BC в точках D и E соответственно. Найдите отрезок DE, если AB = 18 см

Объяснение:

1) АМ=МВ=9 см . По т. о точке пересечения медиан .

2) Т.к. стороны угла ∠ВСМ пересекают две параллельные прямые АВ и DE, по т. о пропорциональных отрезках или

3) Т.к. стороны угла ∠АСМ пересекают две параллельные прямые АВ и DE, по т. о пропорциональных отрезках или

📽️ Видео

Медианы | Свойства медиан | Точка пересечения медиан на прямой ЭйлераСкачать

№384. Через середину М стороны АВ треугольника ABC проведена прямая,Скачать

🔥 Свойства МЕДИАНЫ #shortsСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Точка пересечения медиан треугольника.Скачать

22 Медианы треугольника пересекаются в одной точкеСкачать

Вычисляем высоту через координаты вершин 1Скачать