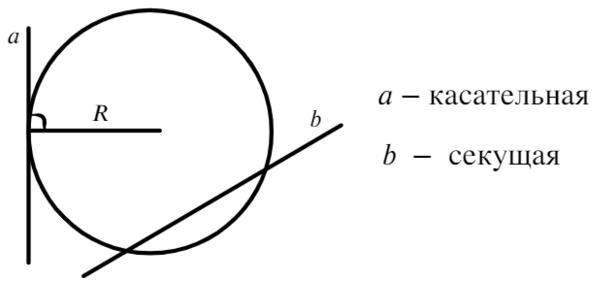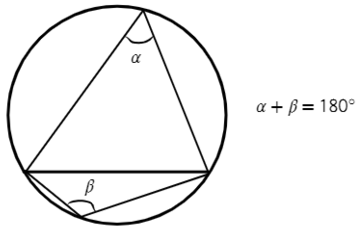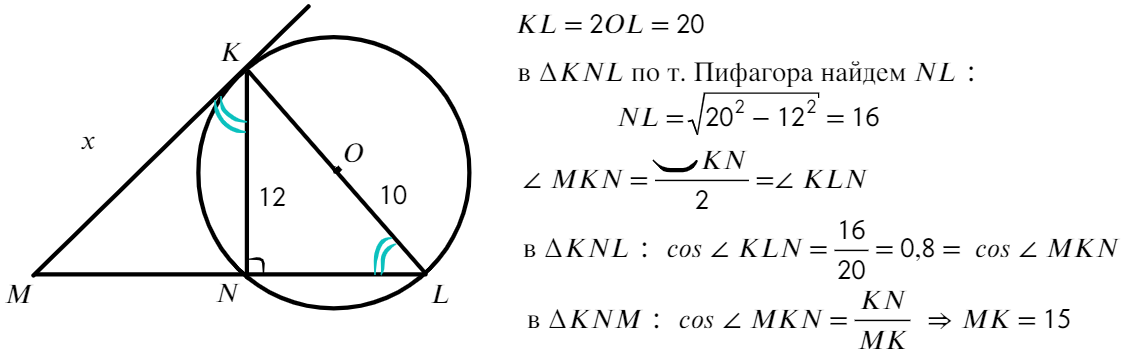Отрезки и прямые, связанные с окружностью Отрезки и прямые, связанные с окружностью |
 Свойства хорд и дуг окружности Свойства хорд и дуг окружности |
 Теоремы о длинах хорд, касательных и секущих Теоремы о длинах хорд, касательных и секущих |
 Доказательства теорем о длинах хорд, касательных и секущих Доказательства теорем о длинах хорд, касательных и секущих |
 Теорема о бабочке Теорема о бабочке |
- Отрезки и прямые, связанные с окружностью
- Свойства хорд и дуг окружности
- Теоремы о длинах хорд, касательных и секущих
- Доказательства теорем о длинах хорд, касательных и секущих
- Теорема о бабочке
- Через точку не лежащую вне окружности можно провести
- Теория и практика окружности
- Аналогично в каждом отрезке присутствует точка, вне окружности (О).
- Задача №1. Дано на рисунке:
- Достаточно вспомнить свойства центральных и вписанных углов.
- Ответ: 39°
- Задача №2. Дано на рисунке:
- Найти нужно меньшую дугу BD
- Ответ: 100°
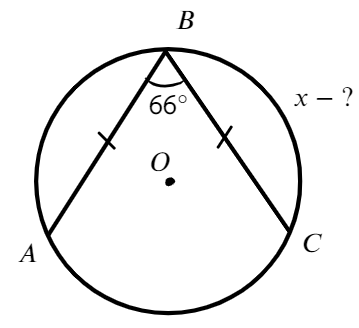
- Найти меньшую дугу ВС
- Ответ: 114°
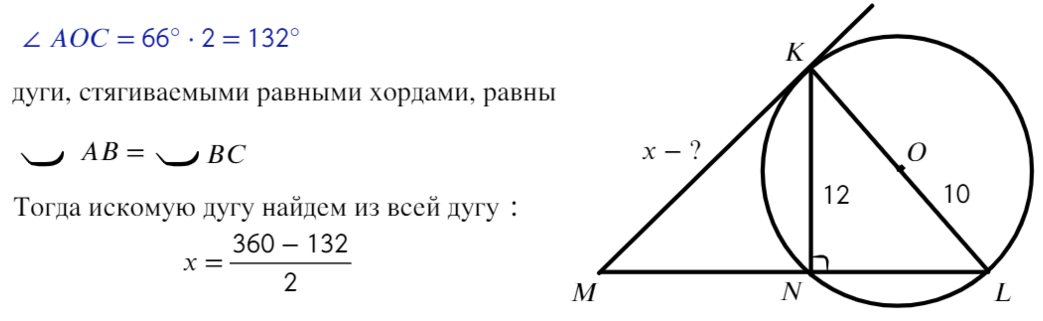
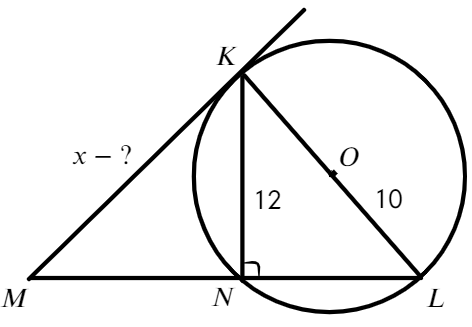
- Задача №4. Дано на рисунке:
- Найти отрезок МК
- Ответ: МК = 15.
- Задача №5. Дано на рисунке:
- Попробуй найти подобные треугольники
- Ответ: 6
- Задача №5. Дано на рисунке:
- Без свойства секущей и касательной здесь будет тяжело
- Ответ: 12√7.
- Я могу долго тебе показывать, как решать задачи, но без твоих усилий ничего не выйдет.
- О треугольниках О четырехуголниках
- 📽️ Видео
Видео:7 класс, 16 урок, Перпендикуляр к прямойСкачать

Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства | ||||||||||||||||||||||||||
| Окружность |  | |||||||||||||||||||||||||||
| Круг |  | |||||||||||||||||||||||||||
| Радиус |  | |||||||||||||||||||||||||||
| Хорда |  | |||||||||||||||||||||||||||
| Диаметр |  | |||||||||||||||||||||||||||
| Касательная |  | |||||||||||||||||||||||||||
| Секущая |  | |||||||||||||||||||||||||||
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
Видео:Через точку A, лежащую вне окружности, проведены две прямые.Скачать

Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  | Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  | У равных дуг равны и хорды. |
| Параллельные хорды |  | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
 |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Большая из двух хорд расположена ближе к центру окружности.

У равных дуг равны и хорды.

Дуги, заключённые между параллельными хордами, равны.
Видео:через точку А, лежащую вне окружности проведены две прямые. Одна прямая касается.. ФИПИСкачать

Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема | ||||||||||||||||
| Пересекающиеся хорды |  | |||||||||||||||||
| Касательные, проведённые к окружности из одной точки |  | |||||||||||||||||
| Касательная и секущая, проведённые к окружности из одной точки |  | |||||||||||||||||
| Секущие, проведённые из одной точки вне круга |  | |||||||||||||||||
| Пересекающиеся хорды | ||
 | ||
| Касательные, проведённые к окружности из одной точки | ||
 | ||
| Касательная и секущая, проведённые к окружности из одной точки | ||
 | ||
| Секущие, проведённые из одной точки вне круга | ||
 | ||
| Пересекающиеся хорды |
 |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Видео:Через любую точку, лежащую вне окружности ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Видео:№660. Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 32Скачать
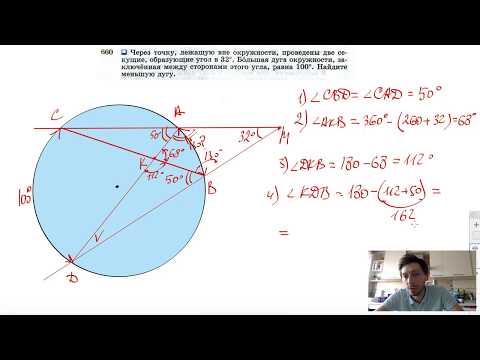
Теорема о бабочке
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Через точку не лежащую вне окружности можно провести
Какое из следующих утверждений верно?
1) В прямоугольном треугольнике гипотенуза равна сумме катетов.
2) Всегда один из двух смежных углов острый, а другой тупой.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
В ответ запишите номер выбранного утверждения.
Рассмотрим каждое из утверждений:
1) «В прямоугольном треугольнике гипотенуза равна сумме катетов» — неверно, по теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
2) «Всегда один из двух смежных углов острый, а другой тупой» — неверно, так как сумма смежных углов равна 180°, следовательно, если один из углов прямой, то смежный ему будет тоже прямой.
3) «Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности» — верно по свойству окружности.
Видео:Построение перпендикуляра к прямойСкачать

Теория и практика окружности
Свойства касательных и секущих.
Площадь, сектор, длина окружности.
Задачи на окружности.
По статистике окружности никто не любит, но при этом леденец любим, солнце любим, давай и окружность полюбим!
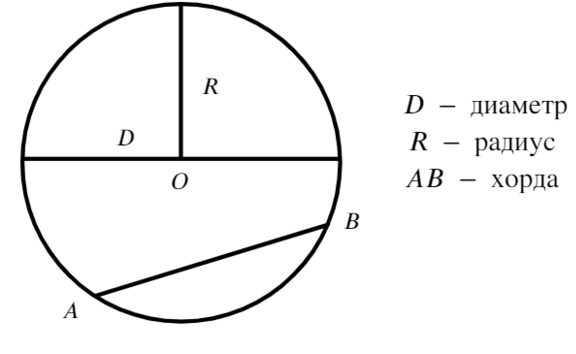
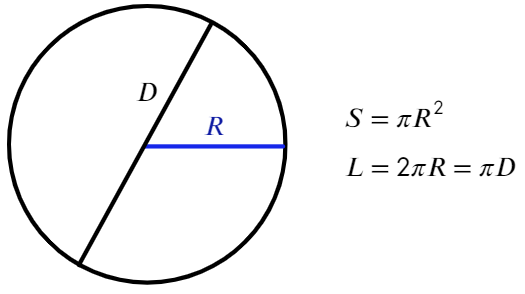
Окружность − геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). На рисунке центр − точка О.
В окружности может быть проведено 3 типа отрезка:
Отрезок, проходящий через две точки окружности, но не через центр, называют хордой (AB).
Хорда, проходящая через центр окружности, называется диаметром (самая большая хорда в окружности − диаметр (D)).
Радиус − отрезок, соединяющий центр окружности с точкой на окружности. Диаметр в два раза больше радиуса (R).
А также две прямые снаружи от окружности:
Касательная имеет одну общую точку с окружностью. Сразу стоит сказать о том, что радиус, проведенный в точку касания, будет иметь с касательной угол 90°.
Секущая пересекает окружность в двух точках, внутри окружности получается хорда или, в частном случае, диаметр.
Теперь чуть-чуть об углах и дугах:
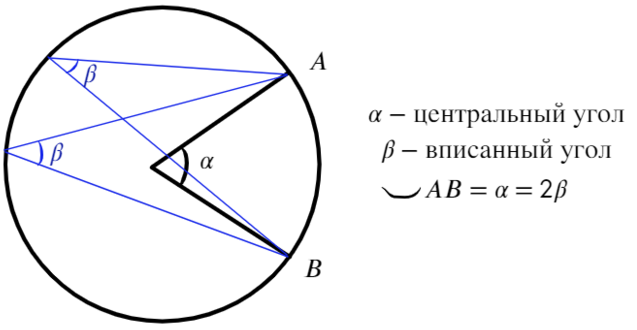
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее. Он в два раза меньше дуги, на которую опирается.
Центральный угол — это угол, вершина которого находится в центре окружности, равен дуге на которую опирается.
Вписанные углы, опирающиеся на одну дугу, равны между собой (β=β=α/2) и равны половине дуги, на которую опираются.
Градусная мера дуги – величина в °, соответствует центральному углу. Длина дуги равна α.
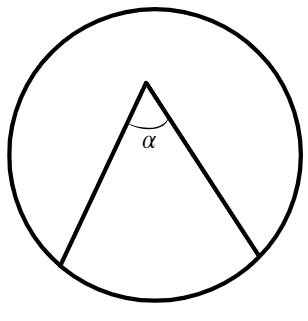
А вот такой угол НЕвписанный, такой угол «никто и звать никак».
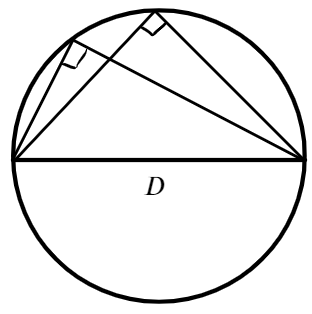
Можно сделать вывод, что вписанный угол, который опирается на половину дуги окружности, будет прямым, а также будет опираться на диаметр:
Любая пара углов, опирающихся на одну и ту же хорду, вершина которых находится по разные стороны от хорды, составляет в сумме 180°.
Запишем основные свойства углов в окружности:
Нашел что-то общее?
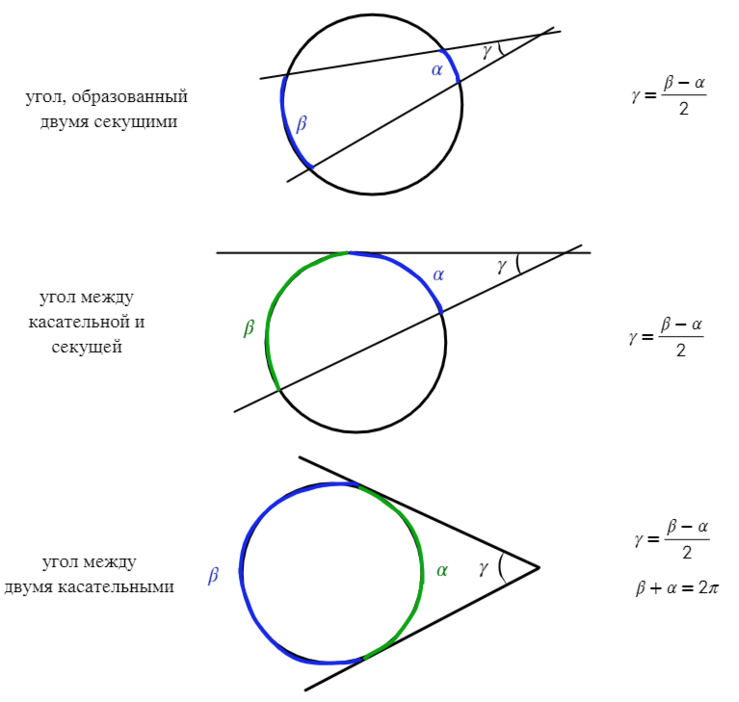
Если угол находится вне окружности, без разницы, чем он получен (касательной или секущей), то найти его можно через половину разности дуг.
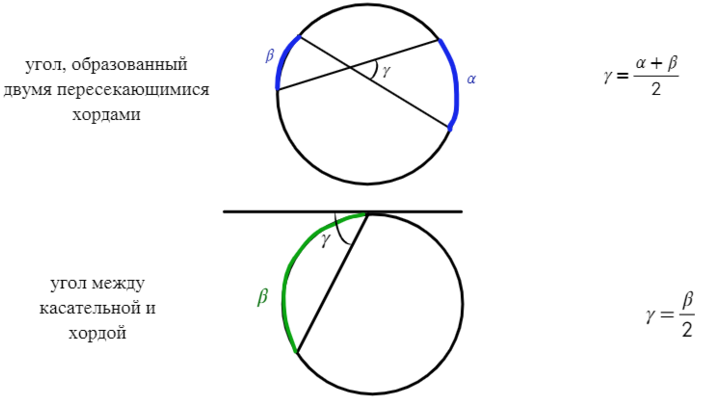
Если угол находится внутри окружности, то находим его через полусумму дуг.
Если есть одна дуга, которая находится на требуемом угле, то угол равен половине этой дуги.
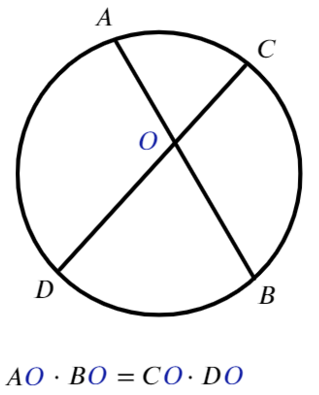
Для любых двух хорд, проходящих через некоторую точку О, выполняет равенство:
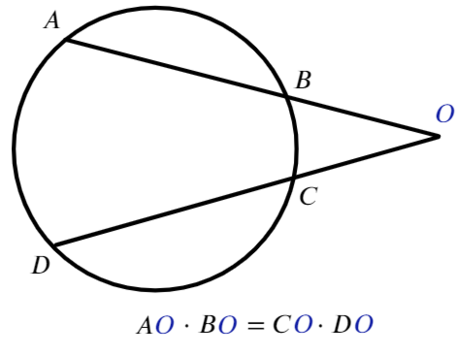
Для любых двух секущих, проходящих через некоторую точку O, выполняется равенство:
Согласен, что они похожи, особенно если не смотреть на картинки.
Как не перепутать такие равенства? В каждом отрезке должна присутствовать точка, вне окружности (О).
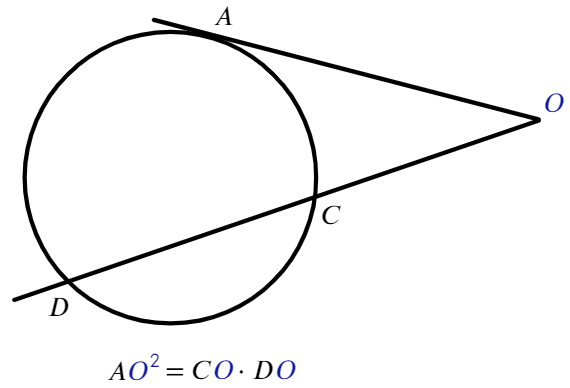
Если из точки, лежащей вне окружности, проведены касательная и секущая:
Аналогично в каждом отрезке присутствует точка, вне окружности (О).
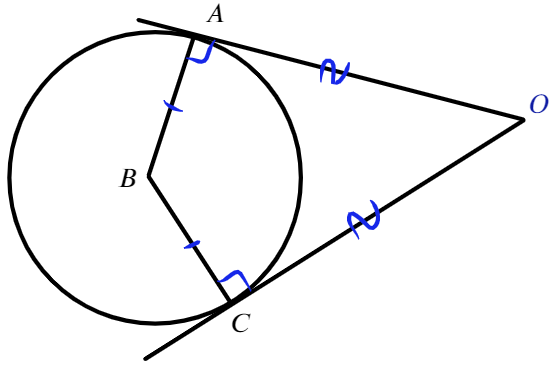
Если теперь провести две касательные из точки O, то получим такие равные отрезки:
Касательные равны, как, сообственно, и радиусы!
Площадь и длина окружности находятся по формуле:
По своему определению число π показывает, во сколько раз длина окружности больше диаметра, отсюда такая формула: L = πD
Если хочешь вывести площадь круга, можешь проинтегрировать длину окружности относительно R или вывести зависимость, как сделал Архимед!
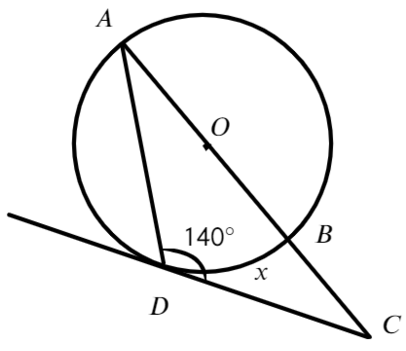
Задача №1. Дано на рисунке:
Достаточно вспомнить свойства центральных и вписанных углов.
Ответ: 39°
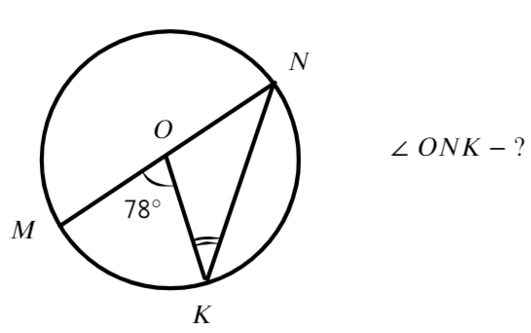
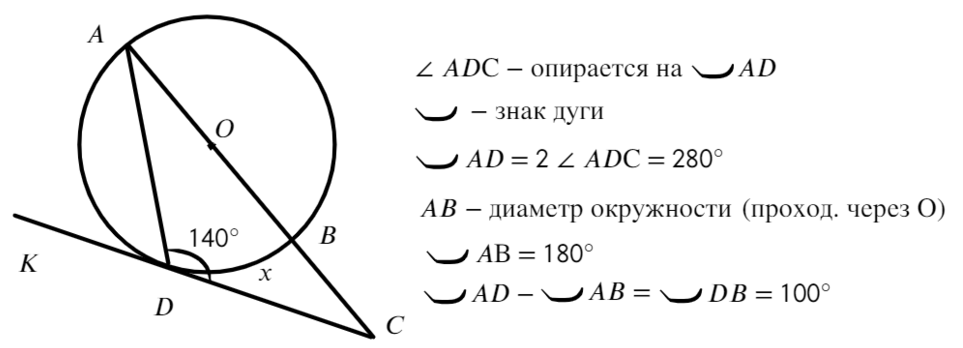
Задача №2. Дано на рисунке:
Найти нужно меньшую дугу BD
Ответ: 100°
Задача №3. Дано на рисунке:
Найти меньшую дугу ВС
Ответ: 114°
Задача №4. Дано на рисунке:
Найти отрезок МК
Ответ: МК = 15.
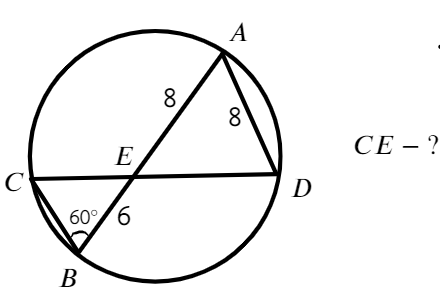
Задача №5. Дано на рисунке:
Попробуй найти подобные треугольники
Ответ: 6
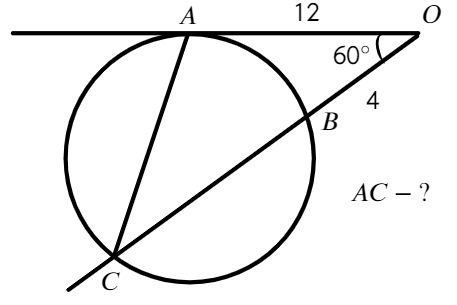
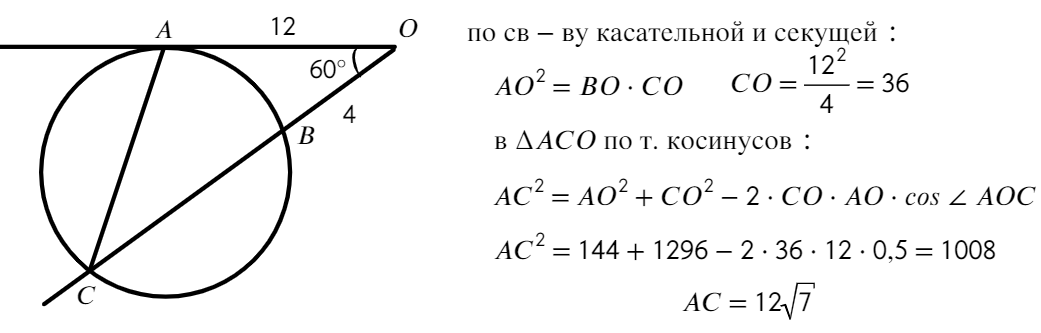
Задача №5. Дано на рисунке:
Без свойства секущей и касательной здесь будет тяжело
Ответ: 12√7.
Я могу долго тебе показывать, как решать задачи, но без твоих усилий ничего не выйдет.
О треугольниках
О четырехуголниках
p.s. Не бойся ошибаться и задавать вопросы!
Если нашел опечатку, или что-то непонятно − напиши.
📽️ Видео
Перпендикуляр к прямой через заданную точку.Скачать

Геометрия 7 класс (Урок№11 - Перпендикуляр к прямой.)Скачать

Геометрия. 7 класс. Теоремы. Т4. Перпендикуляр к прямой.Скачать

Геометрия Через точку A, лежащую вне окружности с центром в точке O, проведены две прямые, однаСкачать

Через точку, не лежащую на данной прямой, можно ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

№672. Через точку А, лежащую вне окружности, проведены две секущие, одна из которых пересекаетСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Построение прямой, параллельной даннойСкачать

Через точку, не лежащую на данной прямой, можно ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Геометрия Через точку A, лежащую вне окружности, проведены две прямые, одна из которых пересекаетСкачать

Построение касательной к окружностиСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать