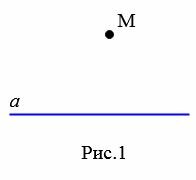
Через точку не лежащую на данной прямой можно провести прямую параллельную перпендикулярно (6 видео)

Аксиома параллельных прямых

Рассмотрим прямую a и точку M, не лежащую на этой прямой (Рис.1). Докажем, что через точку M можно провести прямую, параллельную прямой a.

Через точку не лежащую на данной прямой можно провести прямую параллельную перпендикулярно

Проведем через точку M прямую c, перпендикулярно прямой a, и прямую b, перпендикулярно прямой c (Рис.2).

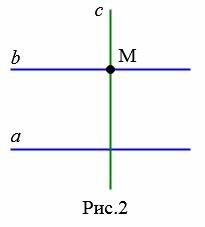Поскольку a и b перпендикулярны прямой с, то они параллельны (статья Перпендикулярные прямые Теорема 1 и статья Параллельные прямые. Признаки параллельности прямых Определение 1). Таким образом через точку M проходит прямая, параллельная прямой a.

Возникает вопрос, существует ли другая прямая, проходящая через точку M параллельно прямой a. Интуитивно ясно, что если немного повернуть прямую b вокруг оси M, то прямые b и a пересекутся. Но доказать это утверждение до сих пор не удалось. основываясь на стальных аксиомах геометрии.

Таким образом имеем это утверждение в виде аксиомы:

Аксиома 1. Через точку, не лежащую на данной прямой проходит только одна прямая, параллельная данной.

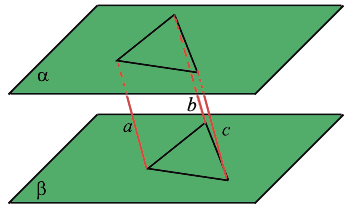
Следствие 1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

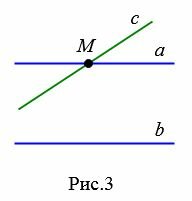Доказательство. Пусть заданы параллельные прямые a и b и пусть прямая c пересекает a в точке M (Рис.3). Докажем, что прямая c пересекает и прямую b.

Предположим обратное, т.е. c не пересекает b. Тогда получается, что через точку M проходят две прямые a и c параллельно прямой b, что невозможно (Аксиома 1). Следовательно прямая с пересекает и прямую b.

Следствие 2. Если две прямые параллельны третьей прямой, то они параллельны.

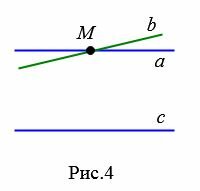Действительно. Предположим, что прямые a и b параллельны прямой c. Докажем, что прямая a параллельна прямой b. Предположим обратное, т.е. прямые a и b пересекаются в точке M (Рис.4). Тогда получается, что через точку M проходят две прямые, параллельные прямой c. Но это невозможно (Аксиома 1). Значит прямые a и b параллельны.

Видео:Перпендикуляр к прямой через заданную точку.Скачать

Параллельность и перпендикулярность прямых и плоскостей в пространстве

Две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости называются скрещивающимися. Прямая и плоскость в пространстве называются параллельными, если они не пересекаются.

Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.

Две плоскости называются параллельными, если они не пересекаются.

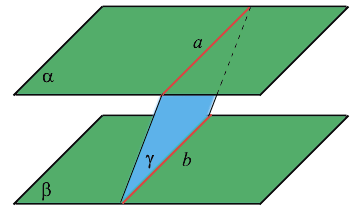
Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны. Через точку, не лежащую в данной плоскости, можно провести параллельную плоскость, и притом только одну.

, так как

Отрезки параллельных прямых между параллельными плоскостями равны.

= =

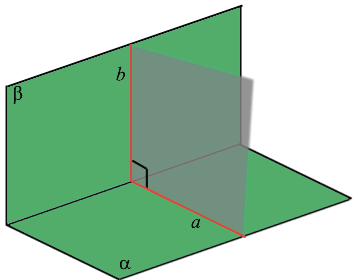
Прямые в пространстве называются перпендикулярными, если они пересекаются под прямым углом. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой в плоскости, проходящей через точку их пересечения.

Прямая, пересекающая плоскость, перпендикулярна плоскости, если она перпендикулярна двум прямым в плоскости, проходящим через точку их пересечения.

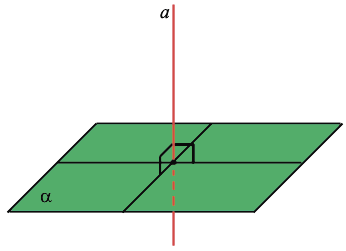
Через каждую точку плоскости можно провести перпендикулярную ей прямую, и только одну. Все прямые, перпендикулярные данной плоскости, параллельны.

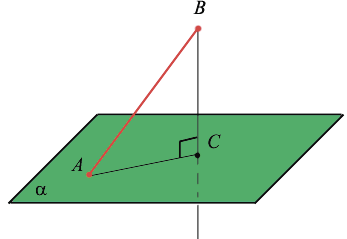
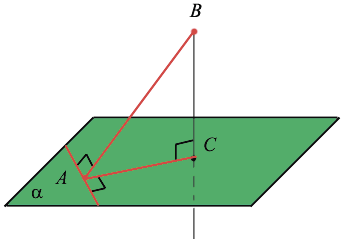
Перпендикуляр, опущенный из данной точки на данную плоскость, — это отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, которая перпендикулярна плоскости. Основание перпендикуляра — это его конец, лежащий в плоскости.

Расстояние от точки до плоскости — это длина перпендикуляра, опущенного от этой точки на плоскость.

Наклонная, проведенная из данной точки к данной плоскости, — это любой отрезок, соединяющий данную точку с точкой плоскости, который не является перпендикуляром к плоскости. Конец отрезка, который лежит в плоскости, — это основание наклонной. Проекция наклонной — это отрезок, который соединяет основания перпендикуляра (точку С) и наклонной (точку А).

Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной. И обратно, если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Две пересекающиеся плоскости называются перпендикулярными, если плоскость, перпендикулярная прямой их пересечения, пересекает данные плоскости по перпендикулярным прямым.

Так как , то .

Поделись с друзьями в социальных сетях:

Видео:Через точку, не лежащую на данной прямой, можно ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Через точку не лежащую на данной прямой можно провести прямую параллельную перпендикулярно

Какое из следующих утверждений верно?

1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.

2) В любой прямоугольник можно вписать окружность.

3) Каждая из биссектрис равнобедренного треугольника является его медианой.

В ответе запишите номер выбранного утверждения.

1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой. — верно.

2) В любой прямоугольник можно вписать окружность. — неверно, в четырехугольник, у которого суммы длин противоположных сторон равны, можно вписать окружность.

3) Каждая из биссектрис равнобедренного треугольника является его медианой. — неверно, верным будет утверждение «Каждая из биссектрис равностороннего треугольника является его медианой».