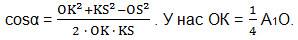Через середину ребра ab куба abcda1b1c1d1 проведена плоскость параллельная прямым bd1 и a1c1

ПОДЕЛИТЬСЯ

Р. К. Гордин ЕГЭ 2020 математика 11 класс геометрия, стереометрия задача 14 (профильный уровень) под редакцией И. В. Ященко соответствует ФГОС.

Ссылка для скачивания пособия задание №14 ЕГЭ: скачать сборник

Р.К.Гордин, Ященко И.В ЕГЭ задание 14 математика 11 класс профильный уровень ФГОС:

Некоторые задания:

1)Дан параллелепипед ABCDA1B1C1D1. Постройте прямую пересечения плоскостей BB1D1 и АВС1.

2)Основание пирамиды SABCDEF — шестиугольник ABCDEF, противоположные стороны которого попарно равны и параллельны. Постройте прямую пересечения плоскостей ASD и CSF.

3)Дана шестиугольная призма ABCDEFA1B1C1D1E1F1, основания которой — правильные шестиугольники. Точка О —центр основания ABCDEF, М— середина бокового ребра DDV Постройте прямую пересечения плоскости А1В1С1 с плоскостью, проходящей через точки О и М параллельно прямой АЕ.

4)Дана четырёхугольная пирамида SABCD, основание которой — параллелограмм ABCD. Точка М лежит на боковом ребре SC. Постройте точку пересечения прямой ВМ с плоскостью ASD.

5)Точки М и N — середины рёбер соответственно АС и треугольной призмы АВСА1В1С1. а) Постройте прямую пересечения плоскостей MNC1 и А1С1 б) В каком отношении плоскость MNC, делит ребро АВ?

6)Основание шестиугольной пирамиды SABCDEF — правильный шестиугольник ABCDEF. Точки М и N — середины рёбер SA и SC соответственно. а) Постройте сечение пирамиды плоскостью, проходящей через точки М, N и В. б) В каком отношении плоскость сечения делит отрезок, соединяющий вершину S с центром основания пирамиды?

7)Основание шестиугольной пирамиды SABCDEF — правильный шестиугольник ABCDEF. Точка М — середина ребра ВС. а) Постройте прямую пересечения плоскостей FSM и ASB. б) В каком отношении плоскость FSM делит отрезок, соединяющий точку А с серединой ребра SD?

8)Основание пирамиды SABCD—параллелограмм ABCD. Точка К лежит на ребре SD и отлична от S и D. а) Может ли сечение пирамиды плоскостью, проходящей через прямую АВ и точку К, быть параллелограммом? б) Пусть К — середина ребра SD, М — середина ребра АВ, а пирамида SABCD правильная, причём все её рёбра равны. Найдите угол между прямыми АК и SM.

9)Дана четырёхугольная пирамида SABCD, основание которой — прямоугольник ABCD, а высота проходит через центр О основания. Через середину А1 бокового ребра SA проведена плоскость а, параллельная плоскости основания, а через середину С1 бокового ребра SC и ребро АВ — плоскость b. Найдите угол между плоскостями а и 13, если АВ : ВС: SA = 8: 6:13.

10)Дана правильная четырёхугольная пирамида SABCD с вершиной S. Все рёбра пирамиды равны, Е —середина бокового ребра SC. Найдите углы между плоскостями: a) SAD и SBC; б) АВС и SCD; в) АВС и BDE; г) BSC и DSC; д) АВЕ и АВС.

11)Дана правильная шестиугольная пирамида SABCDEF с вершиной S. Стороны основания равны 1, боковые рёбра равны 2. Точка G — середина ребра SC. Найдите расстояния: а) от точки S до прямой BF; б) от точки В до прямой SA; в) от точки F до прямой BG; г) от точки А до прямой SD; д) от точки А до прямой SC; е) от точки А до плоскости SDE; ж) от точки А до плоскости SBF; з) от точки А до плоскости SCE.

12)Высота PC треугольной пирамиды РАВС с вершиной Р проходит через точку С. Прямые РА и ВС перпендикулярны. а) Докажите, что основание пирамиды — прямоугольный треугольник. б) Найдите углы, которые образуют боковые рёбра РА и РВ с плоскостью основания, если АС = 6, ВС — 8, а расстояние от точки Р до прямой АВ равно 5.

13)Точка М — середина ребра АВ правильного тетраэдра DABC. а) Докажите, что ортогональная проекция точки М на плоскость ACD лежит на медиане АР грани ACD. б) Найдите угол между прямой DM и плоскостью ACD.

14)Дана правильная четырёхугольная пирамида РАВCD с вершиной в точке Р. Через точку С и середину ребра АВ перпендикулярно к основанию пирамиды проведена плоскость а. а) Докажите, что плоскость а делит ребро ВР в отношении 2: 1, считая от точки В. б) Найдите площадь сечения пирамиды плоскостью а, если известно, что РА = 10, АС = 16.

15)Через середину ребра АВ куба ABCDA1B1C1D1 проведена плоскость, параллельная прямым BD1 и А1С1. Докажите, что эта плоскость делит диагональ DB1 в отношении 3 : 5, считая от от вершины D.

16)Высота конуса равна 6, а радиус основания равен 8. а) Докажите, что наибольшая площадь сечения конуса плоскостью, проходящей через его вершину, равна 50. б) Найдите расстояние от центра основания конуса до этой плоскости.

17)В окружность основания конуса с вершиной Р вписан правильный шестиугольник ABCDEF. а) Докажите, что объём пирамиды PABD вдвое больше объёма пирамиды PDEF. б) Найдите площадь сечения конуса плоскостью АВР, если радиус основания конуса равен 6, а длина его образующей равна 9.

18)На ребре SD правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка М, причём SM: MD = 1:4. Точки Р и Q — середины рёбер ВС и AD соответственно. а) Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией. б) Найдите отношение объёмов многогранников, на которые плоскость MPQ разбивает пирамиду.

19)В правильной треугольной пирамиде SABC сторона АВ основания АВС равна 12, а боковое ребро SA равно 8. Точки М и N — середины рёбер SA и SB соответственно. Плоскость а проходит через прямую MN и перпендикулярна плоскости основания пирамиды.

Видео:№364. Точка К—середина ребра В1С1 куба ABCDA1B1C1D1. Разложите вектор АК по векторам а = АВ,Скачать

Проверочная работа «13 задание ПРОФИЛЬ ЕГЭ математика»

Видео:№69. Через середины ребер АВ и ВС тетраэдра SABC проведена плоскость параллельно ребру SBСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

ПРОФИЛЬ ЕГЭ математика

1. Дана правильная четырехугольная пирамида SABCD. Плоскость α параллельна прямой АС, проходит через точку В и середину высоты пирамиды.

а) Докажите, что плоскость α делит ребро SD в отношении 2 : 1, считая от точки D.

б) Найдите синус угла между плоскостью α и плоскостью ASC, если угол SAC равен 30°.

2. Боковое ребро правильной треугольной пирамиды SABC равно 6, а косинус угла ASB при вершине боковой грани равен Точка M — середина ребра SC, точка — середина ребра AC.

а) Докажите, что угол между прямыми BM и SA равен углу BMN.

б) Найдите косинус угла между прямыми BM и SA.

3. В основании правильной пирамиды PABCD лежит квадрат ABCD со стороной 9. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.

а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.

б) Найдите площадь сечения пирамиды.

4. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB = 4 и диагональю BD = 7. Все боковые рёбра пирамиды равны 4. На диагонали BD основания ABCD отмечена точка E, а на ребре AS — точка F так, что SF = BE = 3.

а) Докажите, что плоскость CEF параллельна ребру SB .

б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.

5. В конус, радиус основания которого равен 6, вписан шар радиуса 3.

а) Изобразите осевое сечение комбинации этих тел.

б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.

6. В пирамиде SABC в основании лежит правильный треугольник ABC со стороной Точка O — основание высоты пирамиды, проведённой из вершины S.

а) Докажите, что точка O лежит вне треугольника ABC.

б) Найдите объём четырёхугольной пирамиды SABCO.

7. Точка M середина ребра AB правильного тетраэдра DABC.

а) Докажите, что ортогональная проекция точки M на плоскость ACD лежит на медиане AP грани ACD.

б) Найдите угол между прямой DM и плоскостью ACD.

8. Основанием прямой треугольной призмы ABCA₁B₁C₁ является прямоугольный треугольник ABC с прямым углом C. Грань ACC₁A₁ является квадратом.

а) Докажите, что прямые CA₁ и AB₁ перпендикулярны.

б) Найдите расстояние между прямыми CA₁ и AB₁, если AC = 4, BC = 7.

9. Длины всех ребер правильной четырёхугольной пирамиды PABCD с вершиной P равны между собой. Точка M — середина бокового ребра пирамиды AP.

а) Докажите, что плоскость, проходящая через точки B и M и перпендикулярная плоскости BDP, делит высоту пирамиды пополам.

б) Найдите угол между прямой BM и плоскостью BDP.

а) Докажите, что B₁KLM — правильная пирамида.

ПРОФИЛЬ ЕГЭ математика

1. Точки A, B и C лежат на окружности основания конуса с вершиной S, причём A и C диаметрально противоположны. Точка M — середина BC.

а) Докажите, что прямая SM образует с плоскостью ABC такой же угол, как и прямая AB с плоскостью SBC.

б) Найдите угол между прямой SA и плоскостью SBC, если AB = 4, BC = 6 и

2. В кубе ABCDA₁B₁C₁D₁ все рёбра равны 4. На его ребре BB₁ отмечена точка K так, что KB = 3. Через точки K и C₁ построена плоскость α, параллельная прямой BD₁.

б) Найдите угол наклона плоскости α к плоскости грани BB₁C₁C.

3. В основании четырехугольной пирамиды SАВСD лежит параллелограмм АВСD c центром О. Точка N — середина ребра SC, точка L — середина ребра SA.

а) Докажите, что плоскость BNL делит ребро SD в отношении 1 : 2, считая от вершины S.

б) Найдите угол между плоскостями BNL и АВС, если пирамида правильная, SA = 8, а тангенс угла между боковым ребром и плоскостью основания пирамиды равен

4. Основание ABCD призмы — трапеция с основаниями AB = 2CD.

а) Докажите проходит через середину бокового ребра

б) Найдите угол между боковым ребром и этой плоскостью, если призма прямая, трапеция ABCD прямоугольная с прямым углом при вершине B, а BC = CD и

5. В правильной треугольной пирамиде SABC сторона основания AB равна 9, а боковое ребро SA = 6. На рёбрах AB и SC отмечены точки K и M соответственно, причём AK : KB = SM : MC = 2 : 7. Плоскость α содержит прямую KM и параллельна прямой SA.

а) Докажите, что плоскость α делит ребро SB в отношении 2 : 7, считая от вершины S.

б) Найдите расстояние между прямыми SA и KM.

6. Сторона правильной треугольной призмы ABCA₁B₁C₁ равна 8. Высота этой призмы равна 6.

а) Докажите, что плоскость, содержащая прямую и параллельная прямой делит пополам ребро

7. Дана треугольная пирамида DABC, точки M, N, P и Q лежат на рёбрах AB, BC, AD, CD, причём AM : MB = CN : NB = 3 : 1. Точки P и Q — середины рёбер DA и DC соответственно.

а) Докажите, что точки P, Q, M и N лежат в одной плоскости.

б) Найдите отношение многоугольников на которые делит плоскость PQM пирамиду.

8. ABCA ₁ B ₁ C ₁ — правильная призма, сторона AB равна 16. Через точки M и P, лежащие на рёбрах AC и BB1 соответственно, проведена плоскость α, параллельная прямой AB. Сечение призмы этой плоскостью — четырёхугольник, одна сторона которого равна 16, а три другие равны между собой.

а) Докажите что периметр сечения призмы плоскостью α больше 40.

б) Найдите расстояние от точки A до плоскости α, если упомянутый периметр равен 46.

9. В правильной треугольной призме ABCA₁B₁C₁ сторона основания а боковое ребро AA₁ = 5.

а) Найдите длину отрезка A₁K, где K — середина ребра BC.

10. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB = 4 и диагональю BD = 7. Все боковые рёбра пирамиды равны 4. На диагонали BD основания ABCD отмечена точка E, а на ребре AS — точка F так, что SF = BE = 3.

а) Докажите, что плоскость CEF параллельна ребру SB .

б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.

ПРОФИЛЬ ЕГЭ математика

б) Найдите угол между плоскостью α и плоскостью ADD₁.

2. В правильном тетраэдре MNPQ через биссектрисы NA и QB граней MNP и QNP проведены параллельные плоскости.

а) Найдите отношение суммы объемов отсекаемых от MNPQ тетраэдров к объему MNPQ

б) Найдите расстояние между NA и QB, если ребро тетраэдра равно 1.

а) Докажите, что прямые B₁P и QB перпендикулярны.

б) Найдите площадь сечения куба плоскостью, проходящей через точку P и перпендикулярной прямой BQ, если ребро куба равно 10.

4. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В₁ и С₁, причем ВВ₁ — образующая цилиндра, а отрезок АС₁ пересекает ось цилиндра.

а) Докажите, что угол АВС₁ прямой.

б) Найдите площадь боковой поверхности цилиндра, если AB = 20, BB₁ = 15, B₁C₁ = 21.

5. Дана треугольная пирамида DABC, точки M, N, P и Q лежат на рёбрах AB, BC, AD, CD, причём AM : MB = CN : NB = 3 : 1. Точки P и Q — середины рёбер DA и DC соответственно.

а) Докажите, что точки P, Q, M и N лежат в одной плоскости.

б) Найдите отношение многоугольников на которые делит плоскость PQM пирамиду.

6. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 12 и Длины боковых рёбер пирамиды SA = 5, SB = 13, SD = 10.

а) Докажите, что SA — высота пирамиды.

б) Найдите расстояние от вершины A до плоскости SBC.

7. а) Дан прямоугольный параллелепипед Докажите, что все грани тетраэдра — равные треугольники (тетраэдр, обладающий таким свойством, называют равногранным).

8. В правильной треугольной призме ABCA₁B₁C₁ все рёбра равны 1.

а) Докажите, что прямая AB₁ параллельна прямой, проходящей через середины отрезков AC и BC₁.

б) Найдите косинус угла между прямыми AB₁ и BC₁.

9. Прямоугольник ABCD и цилиндр расположены таким образом, что AB — диаметр верхнего основания цилиндра, а CD лежит в плоскости нижнего основания и касается его окружности, при этом плоскость прямоугольника наклонена к плоскости основания цилиндра под углом 60°.

а) Докажите, что ABCD — квадрат.

б) Найдите длину той части отрезка BD, которая находится снаружи цилиндра, если радиус цилиндра равен

а) Докажите, что плоскость EFT проходит через вершину D₁.

б) Найдите угол между плоскостью EFT и плоскостью BB₁C₁.

ПРОФИЛЬ ЕГЭ математика

а) В каком отношении плоскость ETD₁ делит ребро BB₁?

б) Найдите угол между плоскостью ETD₁ и плоскостью AA₁B₁.

2. В основании прямой треугольной призмы ABCA₁B₁C₁ лежит равнобедренный треугольник ABC с основанием AC. Точка K — середина ребра A₁B₁, а точка M делит ребро AC в отношении AM : MC = 1 : 3.

а) Докажите, что KM перпендикулярно AC.

б) Найдите угол между прямой KM и плоскостью ABC, если AB = 12, AC = 16 и AA₁ = 6.

3. В треугольной пирамиде SABC известны боковые рёбра: Основанием высоты этой пирамиды является середина медианы CM треугольника ABC. Эта высота равна 4.

а) Докажите, что треугольник ABC равнобедренный.

б) Найдите объём пирамиды SABC.

4. В основании правильной треугольной призмы ABCA₁B₁C₁лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A₁C₁.

а) Постройте сечение призмы плоскостью BAN.

б) Найдите периметр этого сечения.

5. В основании MABCD лежит прямоугольник ABCD со сторонами AB = 4 и BC = все боковые ребра пирамиды равны 4. На диагонали BD основания ABCD отмечена точка Е, а на ребрах AM и AB — точка F и G соответственно так, что MF = BE = BG = 3.

а) Докажите, что плоскость GEF проходит через точку C.

б) Найдите длину отрезка, по которому плоскость GEF пересекает грань CMD пирамиды.

6. Длина ребра правильного тетраэдра ABCD равна 1. M — середина ребра BC, L — середина ребра AB.

а) Докажите, что плоскость, параллельная прямой CL и содержащая прямую DM, делит ребро AB в отношении 3 : 1, считая от вершины A.

б) Найдите угол между прямыми DM и CL.

7. Дана пирамида SABC, в которой

а) Докажите, что ребро SA перпендикулярно ребру BC.

б) Найдите расстояние между ребрами BC и SA.

8. Радиус основания конуса равен 12, а высота конуса равна 5.

а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие.

б) Найдите расстояние от плоскости сечения до центра основания конуса.

9. В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ сторона основания AB = 6, а боковое ребро На рёбрах AB, A₁D₁ и C₁D₁ отмечены точки M, N и K соответственно, причём AM = A₁N = C₁K = 1.

а) Пусть L — точка пересечения плоскости MNK с ребром BC. Докажите, что MNKL — квадрат.

б) Найдите площадь сечения призмы плоскостью MNK.

10. В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 4, точка N — середина ребра AC, точка O центр основания пирамиды, точка P делит отрезок SO в отношении 3 : 1, считая от вершины пирамиды.

а) Докажите, что прямая NP перпендикулярна прямой BS.

б) Найдите расстояние от точки B до прямой NP.

Видео:№196. Изобразите куб ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через:Скачать

ЕГЭ ФИПИ-2015, задача 16 (варианты 14, 15)

Вариант 14

Две параллельные плоскости, находящиеся на расстоянии 8 друг от друга, пересекают шар. Получившиеся сечения одинаковы, и площадь каждого из них равна 9π.

а) Постройте эти сечения.

б) Найдите площадь поверхности шара.

Решение. Всякое сечение шара плоскостью есть круг.

Каждая из плоскостей удалена от центра шара на 4, представляет собой круг, радиус которого равен 3.

9π=πr 2 ⇒ r 2 =9 ⇒ r=3.

Тогда радиус шара ОА=5 (египетский треугольник имеет стороны 3; 4; 5). Площадь поверхности шара S=4πR 2 ; S=4π·5 2 =100π (кв. ед.).

Вариант 15

а) Постройте сечение куба плоскостью, проходящей через середины его рёбер АВ, В₁С₁, АD.

б) Найдите угол между плоскостью A₁BD и плоскостью, проходящей через середины рёбер АВ, В₁С₁, АD.

Середина АВ – точка М; середина В₁С₁ – точка N, середина AD – точка P. Проведем прямую МР – пересечения плоскости MNP с основанием. Секущая плоскость MNP пересечет верхнее основание по прямой, проходящей через точку N параллельно МР, и эта прямая NE пересечет C₁D₁ в точке Е — середине C₁D₁. Прямая МР пересечет CD в точке Х. Таким образом, секущая плоскость имеет с гранью CC₁D₁D две общие точки Е и Х, поэтому пересечет эту грань по прямой EF, причем точка F – середина DD₁. Прямая МР пересечет ВС в точке У. Тогда плоскость MNP пересечет грань ВВ₁С₁С по прямой УN и пересечет ВВ₁ в точке Z, которая также является серединой ВВ₁. Переднюю грань куба плоскость MNP пересечет по прямой ZМ. Итак, мы построили сечение куба плоскостью, проходящей через середины его рёбер АВ, В₁С₁, АD. Получился правильный шестиугольник MZNEFP.

Плоскость A₁BD – правильный треугольник, стороны которого являются диагоналями равных квадратов – граней куба. Плоскости MNP и A₁BD имеют две общие точки Q и Q₁, следовательно, пересекутся по прямой QQ_1.

Найдем угол между плоскостью A₁BD и плоскостью MNP. Это будет угол, образованный двумя полупрямыми, перпендикулярными QQ₁ – линии пересечения наших плоскостей. Построим этот угол.

Проведем A₁О, где О – пересечение диагоналей квадрата ABCD. Медиана A₁О в равностороннем ∆BA₁D является и высотой. A₁О пересечет в точке К отрезок QQ₁, который делит стороны A₁B и A₁D в отношении 1 : 4, считая от точек В и D, следовательно, и ОК : A₁О = 1 : 4.

Почему в отношении 1: 4? Смотрите:

Медиана BQ в этом треугольнике, проведенная к гипотенузе, равна половине гипотенузы, т.е.

Следовательно, BQ : A₁B = 1 : 4. Аналогично, DQ₁ : A₁D =1 : 4. Треугольники A₁QQ₁ и A₁BD подобны по двум пропорциональным сторонам и углу ВА₁D между этими сторонами. QQ₁ II BD, треугольники QA₁K и BA₁O также подобны по углам, образованным соответственно параллельными сторонами, поэтому и ОК : A₁О = 1 : 4.

Так как А₁О ⊥ BD и QQ₁ II BD, то А₁О ⊥ QQ₁, а значит и OK⊥QQ₁.

Так как BD || MP и BD || QQ₁, то MP || QQ_1.

Обозначим через S точку пересечения MP с АС — диагональю квадрата АBСD.

KS – расстояние от МР до QQ₁, т.е. KS ⊥QQ₁ и угол OKS – линейный угол между плоскостью A₁BD и плоскостью MNP. Обозначим угол OKS через α. Проведем KT⊥OS. Треугольник OKT подобен треугольнику OA₁A и OT:OA=OK:ОА₁=1:4.

Так как в ∆OKS высота КТ является и медианой, то ∆OKS – равнобедренный. КТ– биссектриса искомого угла α. Обозначим угол А₁ОА через φ. Из прямоугольного ∆OAA₁ найдем

Углы при основании OS равнобедренного треугольника OKS равны φ, следовательно, угол α = 180°-2φ. Тогда tgα = tg(180 0 -2φ) = -tg2φ.

А можно решить так: установим, что ∆OKS – равнобедренный и проведем SL⊥OK.

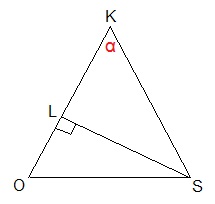
Из прямоугольного треугольника SLK, по определению тангенса острого угла, следует, что tgα = SL : KL. Обозначим KL = x.

Из ∆KLS по теореме Пифагора: SL 2 =KS 2 -KL 2

Из ∆ОLS по теореме Пифагора: SL 2 =ОS 2 -ОL 2 . Левые части равенств равны, значит, и правые части равенств будут равны:

KS 2 -KL 2 = ОS 2 -ОL 2 . Подставляем данные:

Однако, на мой взгляд, самым целесообразным (естественным) было бы рассуждать так:

установили, что угол OKS – искомый и обозначили его через α. Применим теорему косинусов к этому треугольнику и выразим косинус α.

Высота А₁О в правильном треугольнике ВА₁D равна произведению стороны А₁В на синус 60° (катет, противолежащий углу, равен произведению гипотенузы на синус этого угла). Если ребро куба обозначить через а, то

где r₆ – радиус окружности, вписанной в правильный шестиугольник MZNEFP.

Если обозначить сторону правильного шестиугольника через b, то радиус вписанной окружности

Подставляем значения OK, KS, OS и найдем косинус α.

Дорогие друзья, мы решили данную задачу тремя способами (но понятно, что способов больше!), и вы должны знать, что вольны выбирать любой способ решения. Проверяющие вас экзаменаторы зачтут любое обоснованное решение. Да, ну а все же, давайте убедимся в том,

🎬 Видео

В правильной четырёхугольной призме ABCDA1B1C1D1 ребро АА1 равно 15, а диагональ BD1 равна 17.Скачать

№114. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте на ребре АВ точку М. Постройте сечение паралСкачать

№176. Через сторону AD ромба ABCD проведена плоскость ADM так, что двугранный угол BADM равенСкачать

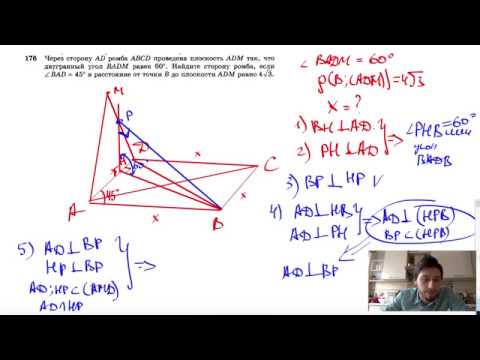
№84. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящейСкачать

№131. В тетраэдре ABCD точка М — середина ребра ВС, АВ = AC, DB = DC. Докажите, что плоскостьСкачать

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

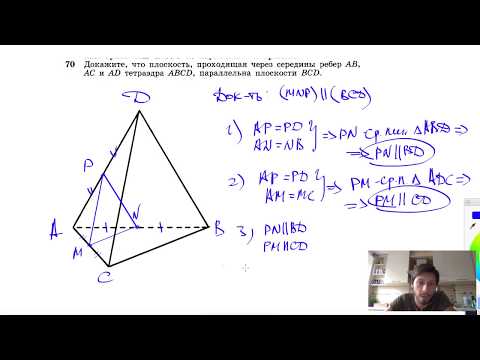
№70. Докажите, что плоскость, проходящая через середины ребер АВ, АС и AD тетраэдра ABCD,Скачать

Геометрия 10 класс Мерзляк 5.44Скачать

№194. Ребро куба равно а. Найдите расстояние между скрещивающимися прямыми, содержащимиСкачать

№190. Дан куб ABCDA1B1C1D1. Найдите следующие двугранные углы: а) АВВ1ССкачать

№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать

№81. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки М и N соответственноСкачать

№402. Даны координаты четырех вершин куба ABCDA1B1C1D1: А (0; 0; 0), В (0; 0; 1), D (0; 1; 0)Скачать

№76. Дан параллелепипед ABCDA1B1C1D1. Докажите, что AC||A1C1 и BD||B1D1.Скачать

№191. Дан куб ABCDA1B1C1D1. Докажите, что плоскостиСкачать

№110. Докажите, что в параллелепипеде ABCDA1B1C1D1 плоскость A1DB параллельна плоскости D1CB1.Скачать

№88. Параллельные прямые АС и BD пересекают плоскость α соответственно в точках А и В. Точки С и DСкачать