Черчение начертить дугу окружности

Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.

Точка, от которой одинаково удалены все точки окружности, называется центром окружности. Центр окружности обычно обозначают большой латинской буквой O:

Окружность делит плоскость на две области — внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это круг:

Видео:Сопряжение окружностейСкачать

Построение окружности циркулем

Для построения окружности используют специальный прибор — циркуль:

Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:

Видео:Черчение. Внутреннее, внешнее и смешенное сопряжение двух окружностей.Скачать

Радиус, хорда и диаметр

Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:

Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r.

Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.

Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:

Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:

Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:

Для обозначения дуг используется символ :

• AFB — дуга с концами в точках A и B, содержащая точку F;
• AJB — дуга с концами в точках A и B, содержащая точку J.

О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.

Хорда AB стягивает дуги AFB и AJB.

Видео:1 2 4 сопряжение окружностейСкачать

Окружность. Круг. Приемы работы циркулем, использование трафаретов

Цели и задачи:

• Дать определение окружность, круг.
• Научить делить окружность на равные части.
• Научить выполнять геометрические построения при помощи циркуля и трафаретов.
• Ознакомить с применением данных геометрических построений в различных областях деятельности человека.
• Воспитывать терпение, аккуратность при выполнении заданий.

Тип урока: комбинированный.

Формы работы: индивидуальная, групповая.

Видео:Внешнее сопряжение двух дуг окружностей третьей дугой. Урок13.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Ход занятия:

Организационный момент:

Проверка готовности к уроку.

Повторение:

Анализ графического упражнения.

Новый материал:

Рубрика «Это интересно!»

С незапамятных времен человек использовал в своей жизни простейшие геометрические построения. Одним из таких построений является деление окружности на равные части. Примеров можно привести много. Превращение колеса из сплошного диска в обод со спицами поставило человека перед необходимостью распределить спицы в колесе равномерно.

С делением окружности неразрывно связано построение правильных многоугольников. Правильные многоугольники встречаются в древнейших орнаментах у всех народов.

В декоративно- прикладном искусстве дизайнеры, ювелиры и представители многих других профессий с успехом применяли деление окружности, создавая прекрасные произведения. Это ордена, медали, монеты и ювелирные украшения.

Орден Красной Звезды
Орден Отечественной войны

Самым распространенным примером применение деления окружности на равные части является создание логотипов, эмблем, товарных знаков различных фирм. Иногда достаточно увидеть эмблему на капоте или крыле автомобиля и безошибочно назвать марку.

Показ наглядных пособий использования геометрических построений в строительстве, архитектуре, машиностроении, а также природные явления.

Построение круга, окружности.

Круг – это часть плоскости, ограниченная окружностью.

Окружность – замкнутая плоская кривая, все точки которой равноудалены от центра.

Чтобы изобразить круг, достаточно взять блюдце или тарелку и обвести.

Для построения окружности необходимо найти центр. Из центра циркулем провести окружность.

Этапы построения:

1. Начертить квадрат.
2. Разделить стороны квадрата на две равные части, отметить буквами или цифрами.
3. Через полученные точки провести центровую линию (штрихпунктирную) Сначала горизонтальную, затем вертикальную.
4. Пересечение линий отметить точкой О – центр окружности.
5. В точку О поставить ножку циркуля и начертить окружность. Центр окружности является также и центром круга.

Запомнить: в центре должны обязательно пересекаться штрихи, проведенных центровых (осевых) линий, а не точки. В окружностях меньших размеров допускается проводить вместо штрихпунктирных линий тонкие линии построения.

Для построения окружностей и кругов используют трафареты.

Демонстрация, показ.

Деление окружности на равные части.

Любая прямая, проведенная через центр окружности, делит эту окружность на две равные части. Две взаимно перпендикулярные прямые, проведенные через центр окружности, делят эту окружность на 4 равные части.

Окружность можно разделить на 8 равных частей, используя линейку или угольники.

Демонстрация, показ.

Если соединить, полученные при делении точки окружности, то мы получим правильные многоугольники.

При делении окружности на 3, 6, 12 равных частей используют не только угольники, но и циркуль. В результате построения можно увидеть правильный равносторонний треугольник, правильный шестиугольник (рисунок 5)

Демонстрация, показ.

Физкультурная пауза.

Закрепление:

Фрагмент из рабочей тетради.

Приготовь для работы циркуль, карандаш с маркировкой Т и ТМ, линейку, трафарет. Все построения выполняй аккуратно.

Используя трафарет с окружностями, изобрази круг.

Для построения окружности необходимо провести штрихпунктирные линии. Эти линии состоят из штриха и точки. При пересечении они образуют центр окружности и являются центровыми или осевыми линиями.

Установи ножку циркуля в центре пересечения осевых (центровых) линий и проведи окружность.

Этапы построения окружности:

1. Начертить квадрат.
2. Разделить все стороны квадрата на две равные части, отметить полученные точки.
3. Через точки провести центровую линию (штрихпунктирную) карандашом с маркировкой Т. Сначала горизонтальную, затем вертикальную.
4. Пересечение линий отметить точкой О – центр окружности.
5. В точку О поставить ножку циркуля и начертить окружность.

Центр окружности является также и центром круга.

Запомни:
В центре должны обязательно пересекаться штрихи, проведенных центровых (осевых) линий, а не точки.
В окружностях меньших размеров допускается проводить вместо штрихпунктирных линий тонкие линии построения.

Рубрика «ЗАПОМНИ»: круг, окружность, осевая линия, центровая линия, штрихпкнктирная линия.

Видео:Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Построение дуг в КОМПАС

В одной из статей мы рассмотрели способы построения окружностей с помощью команды «Окружность» . Иногда требуется только часть дуги окружности и чтобы не строить окружность целиком, а потом её усекать, легче воспользоваться командой «Дуга»

Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Построение дуги в КОМПАС

• Для построения дуги Вам необходимо вызвать команду «Дуга», которая находится на инструментальной панели «Геометрия»

• По умолчанию представлена команда «Дуга» , которая позволяет построить простую дугу указанием: координат центра дуги, начальной и конечной точек дуги, координат центра дуги, радиуса дуги и начального и конечного угла дуги.

Альтернативный способ запуска команды «Дуга» — использование главного текстового меню. Путь: Черчение — Дуги- Дуга

• Если Вам нужно построить дугу по двум или трем точкам, касательную дугу к кривой, дугу и по двум точкам и углу раствора, то проще всего воспользоваться командой из расширенного списка

О наличии расширенного списка команд говорит черный треугольник в правом нижнем углу пиктограммы команды . Расширенный список команд откроется, если нажать и удерживать левую кнопку мыши на названии или пиктограмме команды. Кроме того, команды из расширенного списка доступны на панели параметров, при выборе любой команды из данной группы.

Например, Вам нужно построить дугу по трем точкам . Вы вызываете команду «Дуга», а на «Дуга по трем точкам» переходите, выбрав соответствующую кнопку на Панели параметров (данный способ возможен на версиях КОМПАС не ранее 17).

Видео:СОПРЯЖЕНИЕ ОКРУЖНОСТИ С ЛИНИЕЙ [pairing the circle with the line]Скачать

Пошаговая инструкция построения простой дуги

• Вызовите команду «Дуга» с Инструментальной панели «Геометрия».

Альтернативный вариант воспользоваться Главным текстовым меню. Путь: Черчение – Дуги- Дуга

• Укажите точку центра дуги, кликнув в нужном месте рабочей области, либо указав координаты X и Y на Панели параметров
• Выберите стиль дуги (по умолчанию строится дуга со стилем линии «Основная»)
• Укажите начальную точку дуги, кликнув в любом месте рабочей области, либо указав радиус дуги (или диаметр) и её начальный угол. Переключатель ввода данных: радиус/диаметр находится на Панели параметров

• Укажите конечную точку дуги, кликнув в любом месте рабочей области, либо указав конечный угол дуги.

• Дуга построена

Видео:Внешнее сопряжение дуги и прямой дугой заданного радиуса. Урок16.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Пошаговая инструкция построения дуги по трем точкам

• Вызовите команду «Дуга» с Инструментальной панели «Геометрия»

• На Панели параметров смените команду на «Дуга по трем точкам»

• Выберите стиль дуги (по умолчанию строится дуга со стилем линии «Основная»)

• Укажите начальную точку дуги, кликнув в нужном месте рабочей области, либо указав координаты X и Y.
• Укажите конечную точку дуги, кликнув в нужном месте рабочей области, либо указав координаты X и Y.
• Укажите произвольную точку дуги, кликнув в нужном месте рабочей области, либо указав координаты X и Y.

Видео:Внутреннее сопряжение двух дуг окружностей третьей дугой. Урок14.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Пошаговая инструкция построения дуги по двум точкам

• Вызовите команду «Дуга» с Инструментальной панели «Геометрия»

• На Панели параметров смените команду на «Дуга по двум точкам»

• Выберите стиль дуги (по умолчанию строится дуга со стилем линии «Основная»)

• Укажите начальную точку дуги, кликнув в нужном месте рабочей области, либо указав координаты X и Y.
• Укажите радиус дуги (или диаметр). Переключатель ввода данных: радиус/диаметр находится на Панели параметров
• Укажите конечную точку дуги, кликнув в нужном месте рабочей области, либо указав координаты X и Y.

Видео:#2.4 Автокад уроки для начинающих: КРУГ, ДУГАСкачать

Пошаговая инструкция построения дуги по двум точкам и углу раствора

• Вызовите команду «Дуга» с Инструментальной панели «Геометрия»

• На Панели параметров смените команду на «Дуга по двум точкам и углу раствора»

• Выберите стиль дуги (по умолчанию строится дуга со стилем линии «Основная»)

• Укажите начальную точку дуги, кликнув в нужном месте рабочей области, либо указав координаты X и Y.
• Укажите угол раствора дуги на Панели параметров.
• Укажите конечную точку дуги, кликнув в нужном месте рабочей области, либо указав координаты X и Y.

Видео:Сопряжение прямой с окружностьюСкачать

Пошаговая инструкция построения дуги касательной к кривой

• Вызовите команду «Дуга» с Инструментальной панели «Геометрия»

• На панели Параметров смените команду на «Дуга, касательная к кривой»

• Укажите кривую, по касательной к которой должна располагаться дуга
• Укажите точку на дуге, кликнув в нужном месте рабочей области, либо указав координаты X и Y.

• Выберите стиль дуги (по умолчанию строится дуга со стилем линии «Основная»)

• Укажите конечную точку дуги, кликнув в нужном месте рабочей области, либо указав координаты X и Y.

Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Как определить длину дуги

Для измерения длины дуги нужно воспользоваться командой Длина кривой, расположенной на инструментальной панели Диагностика

После вызова команды нужно кликнуть по дуге и её длина отобразится в окне Информация

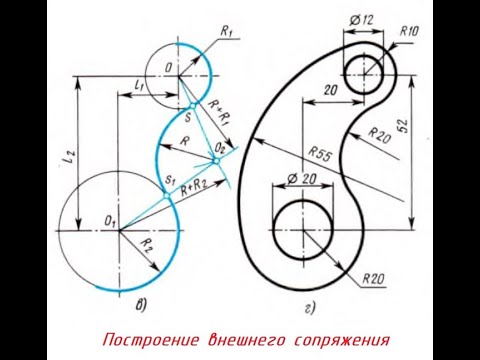
Видео:Построение ВНЕШНЕГО СОПРЯЖЕНИЯСкачать

Как задать длину дуги

Команды построения дуги, в которой в явном виде указывается длина, нет. Обходной путь — проставить размер «Размер дуги окружности» в параметрическом режиме и назначать значения данного размера также не работает. Единственное что можно сделать. Включить Параметрический режим

Поставить к дуге радиальный размер. И вместо значения указать формулу l/(2*M_PI)

После этого на закладке Переменные Панели параметров появится переменная l, которая является длиной дуги и которую можно задавать и управлять радиусом дуги.

В нашем примере значение длины дуги 120, меняя цифры на закладке переменные, мы можем менять радиус.

📺 Видео

Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

[Курс Автокад 2D] Как нарисовать круг (окружность), дугу в AutoCADСкачать

Как задать длину дуги в SolidWorksСкачать

Параметризация длины дуги окружностиСкачать

Видеоуроки по КОМПАС 3D. Урок 1 Деление окружности на равные частиСкачать

Сопряжение окружностей #черчение #сопряжениеСкачать

2 2 3 построение изометрии окружностиСкачать