Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение окружности
- Отрезки в окружности
- Определение окружности
- Отрезки в окружности
- Дуга в окружности
- Углы в окружности
- Длина окружности, длина дуги
- Площадь круга и его частей
- Теорема синусов
- Примеры решений заданий из ОГЭ
- Длина дуги
- Онлайн калькулятор
- Теория
- Формула
- Пример
- Геометрия окружность дуга угол
- Углы, связанные с окружностью
- Вписанные и центральные углы
- Теоремы о вписанных и центральных углах
- Теоремы об углах, образованных хордами, касательными и секущими
- Доказательства теорем об углах, связанных с окружностью
- Геометрия. Урок 5. Окружность
- Определение окружности
- Отрезки в окружности
- Дуга в окружности
- Углы в окружности
- Длина окружности, длина дуги
- Площадь круга и его частей
- Теорема синусов
- Примеры решений заданий из ОГЭ
- Центральные и вписанные углы
- Центральный угол и вписанный угол
- Свойства центральных и вписанных углов
- Примеры решения задач
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности .
Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Видео:Длина дуги окружности. 9 класс.Скачать

Дуга в окружности
Часть окружности, заключенная между двумя точками, называется дугой окружности .
Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .
Теорема 4:
Равные хорды стягивают равные дуги.
Если A B = C D , то ∪ A B = ∪ C D
Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360 ° .
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ A C B – вписанный.
Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Видео:Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Длина окружности, длина дуги
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .
Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
Длина дуги окружности , на которую опирается центральный угол α равна:
l α = π R 180 ∘ ⋅ α
Видео:Вписанные и центральные углы #огэ #огэматематика #математикаСкачать

Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Видео:№1084. Сколько сторон имеет правильный вписанный многоугольник, если дуга описаннойСкачать

Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Видео:8 класс, 33 урок, Градусная мера дуги окружностиСкачать

Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
Видео:8 класс, 34 урок, Теорема о вписанном углеСкачать

Длина дуги
Видео:УГОЛ И ОКРУЖНОСТЬ: центральный угол, вписанный угол, длина дуги окружностиСкачать

Онлайн калькулятор

радиус r =
угол α =
Видео:№653. Найдите вписанный угол ABC, если дуга АС, на которую он опирается, равна: а) 48°; б) 57°Скачать

Теория
Чему равна длина дуги окружности L если её радиус r, а угол между двумя прямыми, проведёнными от центра окружности к конечным точкам дуги — центральный угол α?
Формула
Если угол в градусах:
Если угол в радианах:
Пример
Для примера посчитаем чему равна длина дуги окружности с радиусом r = 2 см и центральным углом α = 45° :
L = 3.14 ⋅ 2 ⋅ 45/180 = 6.28 ⋅ 0.25 = 1.57 см
Видео:Вписанные и центральные углыСкачать

Геометрия окружность дуга угол
Видео:Задача 6 №27885 ЕГЭ по математике. Урок 122Скачать

Углы, связанные с окружностью
 Вписанные и центральные углы Вписанные и центральные углы |
 Углы, образованные хордами, касательными и секущими Углы, образованные хордами, касательными и секущими |
 Доказательства теорем об углах, связанных с окружностью Доказательства теорем об углах, связанных с окружностью |
Видео:Вписанный угол равен половине центрального углаСкачать
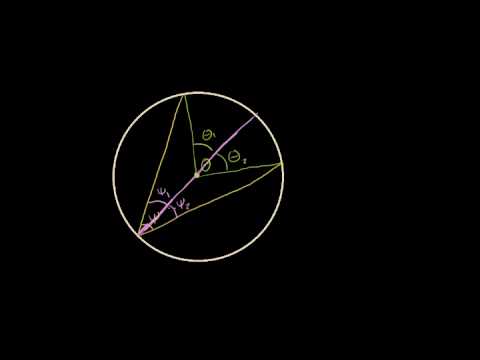
Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Видео:ВПИСАННЫЕ И ЦЕНТРАЛЬНЫЕ УГЛЫ (КРАТКО)Скачать

Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема |
| Вписанный угол |  |
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.





Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.
| Вписанный угол | |||
| Окружность, описанная около прямоугольного треугольника |
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |
Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.


Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами


Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами


Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами


Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
Формула:  |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
 |
Формула:  |
| Угол, образованный касательной и секущей касательной и секущей |
Формула:  |
| Угол, образованный двумя касательными касательными к окружности |
Формулы:  |