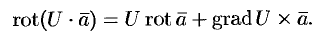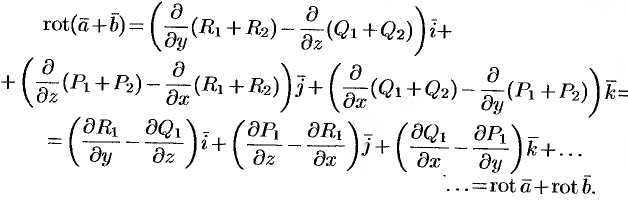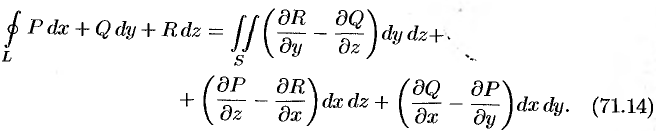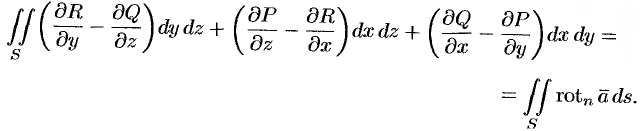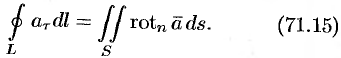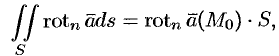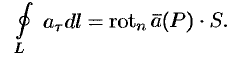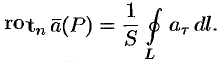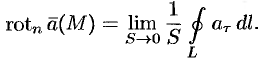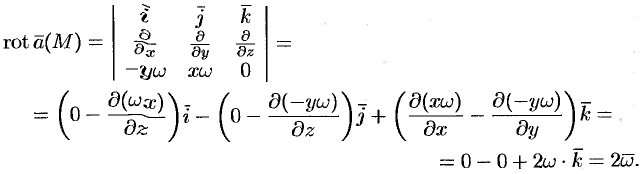Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
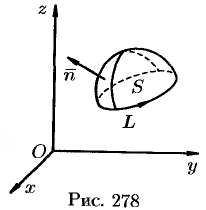
Пусть в некоторой области G задано непрерывное векторное поле а ) к и замкнутый ориентированный контур L. Определение 1. Циркуляцией вектора а по замкнутому контуру L называется криволинейный интеграл 2-го рода от оектора а по контуру L Здесь dr — вектор, длина которого равна дифференциалу дуги L, а направление совпадаете направлением касательной к L, оп- Рис. 31 ределяемымориентацией контура (рис. 31); символ f означает, что интеграл берется по зам1«угому контуру L. ь
Пример 1. вычислить циркуляцию векторного поля вдоль эллипса L: По определению циркуляции имеем Параметрические уравнения данного эллипса имеют вид: , и, значит, . Подставляя эти выражения в формулу (2), найдем Циркуляция векторного поля. Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля Правила вычисления ротора 8.1.
Ротор (вихрь) векторного поля Рассмотрим поле вектора Р, Q, R которого непрерывны и имеют непрерывные частные производные первого порядка по всем своим аргументам. Огределенив 2. Ротором вектора »(М) называется вектор, обозначаемый символом rot а и определяемый равенством или, в символической, удобной для запоминания форме, Этот определитель раскрывают по элементам первой строки, при этом операции умножения элементов второй строки на элементы третьей строки понимаются как операции дифференцирования, например,
Определение 3. Если в некоторой области G имеем rot а = 0, то поле вектора а в области G называете я безвихревым. Пример 2. Найти ротор вектора 4 Согласно формуле (3) имеем Так как rot а — вектор, то мы можем рассматривать векторное поле — поле ротора вектора а. Предполагая, что координаты вектора а имеют непрерывные частные производные второго порядка, вычислим дивергенцию вектора rot а. Получим Таким образом, поле вектора rot а соленоида л ьно.
Теорема 7 (Стокса). Циркуляция вектора а вдоль ориентированного замкнутого контура L равна потоку ротора этого вектора через любую поверхность Е, натянутую на контур L, При этом предполагается, что координаты вектора а имеют непрерывные частные производные в некоторой области G пространства, содержащей поверхность Е, и что ориентация орта нормали п° к поверхности ЕС G согласована с ориентацией контура L так, что из конца нормши обход контура в заданном направлении виден совершающимся против часовой стрелки.
Учитывая, что , и пользуясь определением ротора (3), перепишем формулу (4) в следующем виде: Рассмотрим сначала случай, когда гладкая поверхность Е и ее контур L однозначно проектируются на область D плоскости хОу и ее границу — контур А соответственно (рис. 32). Ориентация контура L порождает определенную ориентацию контура А. Для определенности будем считать, что контур L ориентирован так, что поверхность Е остается слева, так что веетор нормали п к поверхности Е составдя етсосью Oz острый угол 7 (cos 7 >0).
Возможно вам будут полезны данные страницы:
Пусть — уравнение поверхности Е и функция ф(х>у) непрерывна и имеет непрерывные частные производные gf и ^ в замкнутой области D.
Рассмотрим интеграл Линия L лежит на поверхности Е. Поэтому, пользуясь уравнением этой поверхности , мы можем заменить г под знаком интеграла на ^(ж, у). Координаты перемсннойточки кривой А равны координатам соответствующей точки на кривой L, а потому интегрирование по L можно заменить интегрированием по А, Применим к интегралу, стоящему справа, формулу Грина.
Имеем Перейдем теперь от интеграла по области D к интегралу по поверхности Е. Так как dS = cos 7 • da, то из формулы (8) получим, что Вектор нормали п° к поверхности Е определяется выражением к. Отсюда видно, что . Поэтому равенсгво (9) можно переписать так: Считая Е гладкой поверхностью, однозначно проектирующейся на все три координатные плоскости, аналогично убеждаемся в справедливости формул Циркуляция векторного поля.
Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля Правила вычисления ротора Складывая равенства почленно, получим формулу Стокса (5), или, короче, Замечание 1. Мы показали, что поле вектора rote — соленоидальное, и потому поток вектора rota не зависит от вида поверхности Е, натянутой на контур L. Замечание 2. Формула (4) выведена в предположении, что поверхность £ однозначно проектируется на все три координатные плоскости. Бели это условие не выполнено, то разбиваем £ на частя так, чтобы каждая часть указанному условию удовлетворяла, а затем пользуемся аддитивностью интегралов.
- Пример 3:
- Правила вычисления ротора
- Ротор векторного поля. Формула Стокса
- Ротор поля. Формула Стокса
- ЛЕКЦИЯ №6
- 1. Работа электростатического поля.
- 2. Работа поля точечного заряда.
- 3. Теорема о циркуляции.
- 4. Циркуляция и ротор(математическое отступление).
- 5. Ротор в различных системах координат.
- 6. Формула Стокса(математическое отступление).
- 7. Ротор в физике.
- 8. Дивергенция и ротор (Как вы это поняли).
- 9. Потенциальная энергия.
- 10. Разность потенциалов.
- 11. Единица разности потенциалов.
- 12. Потенциал точечного заряда.
- 13. Потенциал системы точечных зарядов.
- 14. Потенциал тела с непрерывным распределением заряда.
- 15. Измерение разности потенциалов.
- 16. Соединение с Землей.
- 17. Гидростатические аналогии.
- 🔍 Видео
Пример 3:
Вычислить циркуляцию вектора по линии 1) пользуясь определением; 2) по теореме Стокса. 4 1) Зададим линию L параметрически: Тогда 2) Найдем rota: Натянем на контур L кусок плосхости Тогда . Инвариантное определение ротора поля Из теоремы Стокса можно получить инвариантное определение ротора поля, не связанное с выбором системы координат. Теорема 8.
Проекция ротора а на любое направление не зависит от выбора системы координат и равна поверхностной плотности циркуляции вектора а по контуру площадки, перпендикулярной этому направлению, Здесь (Е) — плоская площадка, перпендикулярная вектору л; 5 — площадь этой площадки; L — контур площадки, ориентированный так, чтобы обход контура был виден из конца вектора п против хода часовой стрелки; (Е) М означает, что площадка (Е) стягивается к точке М, в которой рассматривается вектор rot а, причем вектор нормали п к этой площадке остается все время одним и тем же (рис. 33). 4
Применим сначала к циркуляции (a,dr) вектора а теорему Стокса, а затем к полученному двойному интегралу — теорему о среднем значении: откуда (скалярное произведение берется в некоторой средней точке Мф площадки (Е)). Пристягивании площадки (Е) кточке М средняяточка Л/ср тоже стремится кточ-ке М и, в силу предполагаемой непрерывности частных производных от координат вектора а (а значит, и непрерывности rot а), мы получаем Поскольку проекция вектора rot а на произвольное направление не зависитотвы-бора системы координат,то и сам вектор rota инвариантен относительно этого выбора.
Отсюда получаем следующее инвариантное определение ротора поля: ротор поля есть вектор, длина которого равна наибольшей поверхностной плотности циркуляции в данной точке, направленный перпендикулярно той площадке, на которой эта наибольшая плотность циркуляции достигается; при этом ориентация вектора rota согласуется с ориентацией контура, при которой циркуляция положительна, по правилу правого винта. 8.3.
| Физический смысл ротора поля Пустьтвердое |
тело вращается вокруг неподвижной оси I с угловой скоростью и. Не нарушая общности, можно считать, что ось I совпадает с осью Oz (рис. 34). Пусть М(г) — изучаемая точка тела, где Вектор угловой скорости в нашем случае равен из = wk, вычислим вектор v линейной скорости точки М, Отсюда Циркуляция векторного поля. Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля.
Правила вычисления ротора
Итак, вихрь поля скоростей вращающегося твердого тела одинаков во всех точках поля, параллелен оси вращения и равен удвоенной угловой скорости вращения. 8.4. Правила вычисления ротора 1. Ротор постоянного вектора с равен нулевому вектору, 2. Ротор обладает свойством линейности постоянные числа. 3. Ротор произведения скалярной функции и<М) на векторную а(М) вычисляется по формуле
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:#8 Ротор/Дивергенция/ГрадиентСкачать

Ротор векторного поля. Формула Стокса
Ротор поля. Формула Стокса
Ротором (или вихрем) векторного поля
называется вектор, обозначаемый 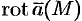
Формулу (71.13) можно записать с помощью символического определителя в виде, удобном для запоминания:
Отметим некоторые свойства ротора.
- Если
— постоянный вектор, то
.
, где
.
, т. e. ротор суммы двух векторов равен сумме роторов слагаемых.
- Если
— скалярная функция, а
— векторная, то
Эти свойства легко проверить, используя формулу (71.13). Покажем, например, справедливость свойства 3:
Используя понятия ротора и циркуляции, векторного поля, запишем известную в математическом анализе (см. п. 58.4) формулу Стокса:
Левая часть формулы (71.14) представляет собой циркуляцию вектора 

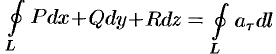
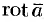


Следовательно, формулу Стокса можно записать в виде
Такое представление формулы Стокса называют ее векторной формой. В этой формуле положительное направление на контуре 

Формула (71.15) показывает, что циркуляция вектора 





Используя формулу (71.14), можно дать другое определение ротора поля, эквивалентное первому и не зависящее от выбора координатной системы.
Для этого применим формулу Стокса (71.15) для достаточно малой плоской площадки 


По теореме о среднем для поверхностного интеграла (п. 57.1, свойство 7) имеем:
где 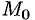

Тогда формулу (71.15) можно записать в виде
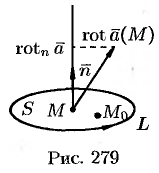
Пусть контур 

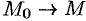
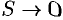
Ротором вектора 




Как видно из определения, ротор вектора 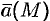
Дадим физическое истолкование понятия ротора векторного поля. Найдем ротор ноля линейных скоростей твердого тела, вращающегося вокруг оси 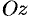
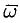
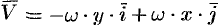
По определению ротора
Ротор этого поля направлен параллельно оси вращения, его модуль равен удвоенной угловой скорости вращения.
С точностью до числового множителя ротор поля скоростей 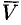
Замечание. Из определения (71.13) ротора вытекает, что направление ротора — это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадке 
Так что связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению (см. п. 70.3).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Ротор векторного поляСкачать

ЛЕКЦИЯ №6
| Потенция (книжн.) — возможность, то, что существует в скрытом виде и может проявиться при известных условиях. (С.И.Ожегов. Словарь . ) |
Видео:Демидович №4437а: ротор скаляра на постоянный векторСкачать

1. Работа электростатического поля.
Из механики известно определение элементарной работы

Вычислим работу по перемещению точечного заряда q силой электростатического поля 

где 
Видео:Оператор Набла. Градиент. Дивергенция. Ротор. Лапласиан.Скачать

2. Работа поля точечного заряда.
Более правильно название данного раздела должно звучать так: «Работа электростатического поля, созданного точечным зарядом Q, по перемещению точечного заряда q из точки 1 в точку 2». Но мы с вами и так понимаем, о чем речь.
Начало координат выбрано в точке, в которой находится заряд Q. Из рис.6.2 видно, что 



Можно сделать вывод, что работа электростатического поля, созданного точечным зарядом, а также любого другого центрально-симметричного поля, не зависит от формы пути, а определяется только начальным и конечным положением.
очевидно, что работа поля при перемещении заряда по замкнутому контуру равна 0.

Видео:РоторСкачать

3. Теорема о циркуляции.
Пусть имеется произвольное электростатическое поле, созданное системой из N точечных зарядов. Тогда на основании принципа суперпозиции (4.5) и формулы (6.4) можно записать
 | Lex: Криволинейный интеграл по произвольному замкнутому контуру от напряженности электростатического поля равен 0.  (6.4) (6.4) |
Такого вида интеграл в математике называется циркуляцией вектора, поэтому вышеприведенный закон это теорема о циркуляции напряженности электростатического поля.
 | rem: Если поле не электростатическое, то закон несправедлив. |
Видео:Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

4. Циркуляция и ротор(математическое отступление).
Как мы видели в пункте 1, работа электростатического поля оказалась равной криволинейному интегралу, вычисленному вдоль траектории, по которой движется заряд.
Вообще в математике криволинейный интеграл от любой векторной функции 


Пусть теперь в области пространства, в которой определено векторное поле 
 | def: Циркуляцией вектора  по произвольному замкнутому контуру L называется криволинейный интеграл Г по произвольному замкнутому контуру L называется криволинейный интеграл Г  , (6.7) где , (6.7) где  — единичный вектор, касательный к контуру L, указывающий направление обхода этого контура. — единичный вектор, касательный к контуру L, указывающий направление обхода этого контура. |
Фактически интегрируется только касательная составляющая векторного поля Аl, поэтому помимо (6.7) для обозначения циркуляции используют ещё следующие эквивалентные формулы:

Будем, кроме того, считать, что на контуре выбрано положительное направление обхода, то есть направление, при движении, вдоль которого область, ограниченная контуром, остаётся всегда слева (более точно см. ниже).
Вновь вспомним о гидродинамике. Если мы рассмотрим векторное поле скоростей 
Следует отметить, однако, что характеризовать завихрённость поля непосредственно циркуляцией Г нельзя, поскольку поле может быть очень неоднородным, и степень его завихрённости будет изменяться от точки к точке. Желая же определить такую «локальную» завихрённость, мы должны будем уменьшать размеры контура L, стягивая его в точку. При этом, очевидно, циркуляция будет стремиться к 0. В связи с этим, для характеристики степени завихрённости поля вводят понятие плотности циркуляции, определяя её как предел, к которому стремится отношение циркуляции вектора 

Вычисляя этот предел, мы будем иметь уже некоторое конечное, отличное от нуля число. Однако, это значение будет зависеть от ориентации контура L в поле. Например, как уже говорилось ранее, от ориентации турбинки в жидкости. Изменяя ориентацию турбинки, мы можем получить максимальное и минимальное значения Г (соответствующие двум противоположным ориентациям турбинки, при этом одно из них будет положительным, а другое отрицательным), а также при некоторой ориентации турбинка вообще перестанет вращаться, что соответствует Г=0. Данные обстоятельства показывают, что всё многообразие значений плотности циркуляции векторного поля может быть, вообще говоря, представлено в виде проекции некоторого вектора, на нормаль к площадке контура L. При этом данный вектор по абсолютной величине будет равен максимальному значению плотности циркуляции вектора 
Данный вектор называется ротором или вихрем векторного поля 

Здесь 
Видео:Александр Чирцов: ротор, дивергенция и градиентСкачать

5. Ротор в различных системах координат.
Исходя из определения (6.10) можно получить проекции 
в декартовых координатах:


Видео:Дивергенция векторного поляСкачать

6. Формула Стокса(математическое отступление).
В математике доказывается следующее соотношение, называемое формулой (теоремой) Стокса, связывающее циркуляцию вектора 
 | Lex: Циркуляция векторного поля  вдоль некоторого замкнутого контура L равна потоку ротора этого векторного поля через поверхность S, опирающуюся (натянутую) на этот контур. вдоль некоторого замкнутого контура L равна потоку ротора этого векторного поля через поверхность S, опирающуюся (натянутую) на этот контур.  , (6.14) , (6.14) |
При этом направление нормали 
Наблюдатель, обходящий контур L и направленный по нормали 
Видео:Демидович №4436.1: значение ротора в точкеСкачать

7. Ротор в физике.
Понятно, что если циркуляция напряженности электростатического поля равна 0, то и

Если поле имеет ротор, отличный от нуля, то оно имеет некоторую завихренность, например, вода, вытекающая из ванны.
Проведем дальнейшие аналогии с гидродинамикой. На реке скорость течения обычно у берегов меньше, чем на фарватере. Деревянная щепка может служить “ротор-метром”. Она будет вращаться во всех точках, кроме строго центральных. Поэтому ротор этого векторного поля скоростей отличен от нуля.
Чтобы построить электрический “ ротор-метр” — по крайней мере в воображении — следует положительные пробные заряды прикрепить к какому-либо центру на изолирующих спицах. Если в поле эта система будет вращаться, то ротор отличен от нуля. Понятно, что размеры нашего прибора должны быть достаточно малы.
Видео:Ротор векторного поля. Гидродинамическая аналогия. Теорема Стокса.Скачать

8. Дивергенция и ротор (Как вы это поняли).
На рис.6.7 представлены различные картины векторного поля. Попробуйте сказать, где ротор и дивергенция равны 0, а где нет. При этом прежде всего нужно обратить внимание на контуры интегрирования, заметив, что они выбраны так, чтобы вдоль каждой из сторон, проекция векторов поля имела одно и тоже значение (причём для двух сторон в случаях а, б, г, д она равна 0).

a)  вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. ротор не равен нулю. Сравните с рекой. | б)  Явно виден источник поля. Дивергенция не равна нулю. Явно виден источник поля. Дивергенция не равна нулю. Поле центрально — симметричное. Поэтому ротор равен 0. | в)  вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Проекции векторов поля на противоположные стороны контура разных знаков, но одинаковы по абсолютной величине, и поэтому при сложении линейных интегралов они уничтожают друг друга. Поэтому ротор равен нулю. |
г)  вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Вектор убывает по мере удаления от центра поля (за пределами рисунка) поэтому ротор может быть равен 0. | д)  вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Вектор не убывает, поэтому линейный интеграл по левой стороне контура не компенсируется таким же интегралом по правой. Поэтому ротор не равен нулю. | е)  Явно виден сток поля. Поэтому дивергенция не равна 0. Явно виден сток поля. Поэтому дивергенция не равна 0. Так же и ротор не равен нулю, поскольку циркуляция вдоль указанного контура не равна 0, так как проекции векторов поля на все стороны контура одного знака (отрицательны) и при сложении (интегрировании) не компенсируют друг друга. |
Подводя итог, ещё раз отметим, что ротор характеризует степень завихрённости векторного поля, его «вращательную составляющую». При этом, однако, нужно иметь в виду, что данная «вращательная компонента» поля может быть обусловлена не только искривлением векторных линий (завихрённость «в чистом виде»), как при вытекании воды из ванны, или в примере е), но и поперечной неоднородностью поля, когда векторные линии — прямые, как в случае течения воды в реке (рис.6.5), или в случае примера а).
Видео:41. Основные понятия теории векторных полейСкачать

9. Потенциальная энергия.
Теперь вспомним механику. Сила называется консервативной, если ее работа не зависит от формы пути. Поле называется потенциальным, если интеграл по замкнутому контуру равен 0. Ясно, что электростатические или кулоновские силы — консервативные, а электростатическое поле потенциальное. Следовательно, можно ввести понятие потенциальной энергии, зная, что работа равна разности потенциальных энергий.

Видео:Демидович №4436а: ротор радиус-вектораСкачать

10. Разность потенциалов.
Из (6.16) и (6.1) следует, что
Видим, что отношение работы поля по перемещению заряда к самому этому заряду есть величина, зависящая только от самого поля, т.е. это скалярная характеристика поля, которую назвали разностью потенциалов.
 | def: Разностью потенциалов между точками 1 и 2 называется отношение работы, совершаемой силой электростатического поля по перемещению заряда между этими точками, к величине этого заряда.  (6.18) (6.18) |
 | rem: · помним, что изменение потенциала  , поэтому будем отличать изменение от разности. , поэтому будем отличать изменение от разности. · Как для любого вида потенциальной энергии, физический смысл имеет не она сама, а ее разность (или изменение). · Линии электростатического поля не могут быть замкнуты, иначе вычислив криволинейный интеграл вдоль этой линии (контура) не получим 0. Линии напряженности могут начинаться и заканчиваться на бесконечности или на зарядах. · Напряженность и потенциал — это два эквивалентных друг другу способа описания электростатического поля. Напряженность — это силовая характеристика, а потенциал — энергетическая. · Если среда — не вакуум, то потенциал и напряженность в e раз меньше, чем в вакууме. Здесь e — диэлектрическая проницаемость среды. |
Видео:ДивергенцияСкачать

11. Единица разности потенциалов.
В честь А.Вольта единица разности потенциалов называется 1 Вольт.
 | def: 1 Вольт — единица СИ разности потенциалов, равная разности потенциалов между двумя точками пространства, при перемещении между которыми заряда в 1 Кулон электростатическое поле совершает работу 1 Джоуль.  (6.19) (6.19) |
Если считать потенциальную энергию на бесконечности равной 0, то можно говорить о потенциале точки пространства. Тогда 1 Вольт — это потенциал точки при перемещении из которой на бесконечность заряда 1 Кл электростатическим полем совершается работа 1 Дж.
Видео:Скалярное и векторное поля. Определения и отличия.Скачать

12. Потенциал точечного заряда.
Мы его вычислили практически в пункте 2. Считая потенциал на бесконечности равным 0, и связывая систему отсчета с зарядом, сразу запишем
 (6.20) График данной зависимости показан на рисунке 6.8. (6.20) График данной зависимости показан на рисунке 6.8. |  |
Видео:Потенциальное поле. Нахождение потенциала векторного поляСкачать

13. Потенциал системы точечных зарядов.
Из (6.18) следует, что


Видео:Найти дивергенцию и ротор векторного поляСкачать

14. Потенциал тела с непрерывным распределением заряда.
Очевидно, что в случае непрерывного распределения заряда по телу (см. рис.4.2), потенциал по аналогии с (4.6), можно записать как

Если плотность заряда 

Интеграл, по прежнему, вычисляется по объему заряженного тела.
Видео:Александр Чирцов про дивергенцию и роторСкачать

15. Измерение разности потенциалов.
Измерить напряженность — весьма непростая задача. Гораздо проще измерить разность потенциалов с помощью электрометров (электростатических вольтметров), устройство и принцип действия которых понятен из рис.6.9.
Измеряется разность потенциалов между стрелкой и корпусом. Так можно измерить разность потенциалов между заряженным проводником и Землей (см. рис.6.10). Электрометр принципиально отличается от электроскопа наличием металлического корпуса. В случае электроскопа роль корпуса играют окружающие предметы, поэтому отклонение стрелки зависит от их расположения. Ясно, что электроскопом измерить разность потенциалов нельзя.
Отметим, что как бы сложна не была форма проводника, электрометр показывает везде один и тот же потенциал (см. рис.6.10).
При попытках измерить потенциал в диэлектрике (в воздухе) на пробном шарике возникнет индукционный заряд, а на стрелке электрометра такой же заряд, но противоположного знака. Возникает сильное искажение первоначального поля. Электрометр, конечно, покажет потенциал стрелки относительно корпуса, однако он будет уже другим.
Следовательно, возникает задача убрать индукционный заряд с пробного шарика. Во-первых, можно подождать довольно долгое время. Тогда заряды сами стекут с пробного шарика, уравняв его потенциал с потенциалом воздуха в данной точке пространства. Во-вторых, этот процесс можно ускорить, ионизовав воздух вокруг шарика. Тогда ионы, разноименные с зарядом шарика, будут переходить на него до тех пор, пока не нейтрализуют индукционный заряд. Так работает электрический зонд. Ионизовать воздух можно различными способами, например, с помощью пламени (пламенный зонд), устройство которого показано на рис.6.11. В-третьих, вместо пробного шарика можно использовать небольшое ведерко с водой. Если в ведре сделать дырку, то утекающая вода будет уносить избыточный заряд.
Перемещая зонд в поле заряженного металлического шара, можно убедиться, что электрометр дает одно и то же показание, если зонд остается на поверхности сферы, центр которой совпадает с центром шара. Если перемещать зонд по радиальным прямым, то показания электрометра будут изменяться сильнее всего.
Видео:ротор от радиус вектора на модуль радиус вектораСкачать

16. Соединение с Землей.
Чтобы разрядить какое-либо тело, мы соединяем его с заземленным предметом, например, с водопроводным краном, или просто касаемся рукой. При этом мы говорим, что «заряды ушли с проводника в землю».
Более точно явление заключается в следующем. Действие электрического поля мы наблюдаем только тогда, когда есть разность потенциалов между рассматриваемым телом и окружающими предметами. Если же соединить это тело с землей, то разность потенциалов между этим телом и окружающими заземленными предметами исчезает, и, следовательно, исчезает электрическое поле.
Следует заметить, что соединение именно с землей не играет принципиальной роли. Наблюдалось бы то же самое, если бы вместо заземленных предметов, например, стен комнаты, был замкнутый проводник изолированный от земли.
Видео:Демидович №4435б: ротор произведенияСкачать

17. Гидростатические аналогии.
В заключении данной лекции вновь вспомним об аналогиях с гидростатикой.
Разность потенциалов можно уподобить разности уровней жидкости в сосуде, а заряд -массе жидкости. Если в двух сообщающихся сосудах уровни жидкости различны, то при их соединении жидкость будет перетекать до тех пор, пока уровни не сравняются (см. рис.6.13). Так же и при соединении двух проводников с разными потенциалами, заряд будет переходить до тех пор, пока не станет равным потенциал. Попробуйте сами определить, какими станут заряды на шарах после их соединения проволокой (рис.6.13).
🔍 Видео
Демидович №4437б: ротор векторного произведенияСкачать










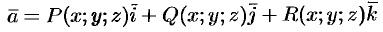
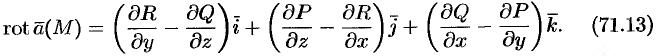
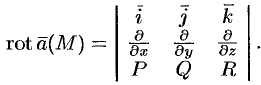
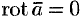 .
.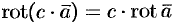 , где
, где 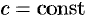 .
.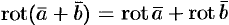 , т. e. ротор суммы двух векторов равен сумме роторов слагаемых.
, т. e. ротор суммы двух векторов равен сумме роторов слагаемых. — скалярная функция, а
— скалярная функция, а