Чем площадь круга отличается от длины окружности

Здесь вы можете рассчитать площадь круга по известным параметрам. Для вычисления достаточно знать радиус, диаметр круга или длину его окружности.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Окружность и круг — в чём отличие?

Часто понятия круг и окружность путают, хотя это разные вещи. Окружность — это замкнутая линия, а круг — это плоская фигура, ограниченная окружностью. Таким образом, гимнастический обруч или колечко — это окружности, а монета или вкусный блин — это круги.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от одной заданной точки — центра окружности.

Круг — бесконечное множество точек на плоскости, которые удалены от заданной точки, называемой центром круга, на значение, не превышающее заданного неотрицательного числа, называемого радиусом этого круга.

Окружность и круг

Видео:Окружность и круг, 6 классСкачать

Урок 25 Бесплатно Длина окружности и площадь круга

На этом уроке мы рассмотрим одни из самых древнейших геометрических фигур: окружность и круг.

Определим, какими элементами характеризуются круг и окружность, в чем сходство и различие этих фигур.

Узнаем, как рассчитать длину окружности и площадь круга.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Окружность и круг

Мы часто встречаем такие понятия, как окружность и круг.

Давайте попробуем разобраться, что называют окружностью, а что кругом.

Окружность — это замкнутая плоская кривая, все точки которой удалены на одинаковые расстояния от заданной точки, называемой центром окружности.

Центр окружности— это точка, которая находится на одинаковом расстоянии (равноудаленная) от любой точки окружности, ее обозначают обычно заглавной буквой О.

По сути, окружность — это изогнутая линия. Наглядно представить данную геометрическую фигуру можно, обведя стакан или блюдце карандашом, — оставшийся нарисованный след и будет окружностью.

Круг — это часть плоскости, ограниченная окружностью. Можно также сказать что это часть плоскости, которая находится внутри линии окружности.

Круг — плоская фигура, ее можно получить, закрасив окружность или вырезав его из бумаги по контуру окружности.

Свои имена окружность и круг приобрели не сразу.

В древние времена специальных названий для этих фигур не существовало. Люди пытались описать различные геометрические формы, сравнивая объекты. Например, говоря про что-то круглое, говорили: «такой, как солнце» или «такой, как орех» и т.п.

Только в Древней Греции окружность и круг приобрели себе свои названия.

Круг всегда привлекал к себе внимание как самая простая фигура из кривых, но самая загадочная.

У меня есть дополнительная информация к этой части урока!

Древние греки считали круг и окружность символом бесконечности и совершенства. Поражало то, что в каждой своей точке окружность устроена одинаково, представляя собой бесконечную линию, которая движется сама по себе.

У древних славян еще за долго до христианства круг был символом солнца.

В Древнем Египте и Греции круг изображали в виде змея Уробороса, который кусает свой хвост, образуя тем самым, окружность — этот символ обозначал бесконечность и цикличность во всей вселенной (смена дня и ночи, жизни и смерти т.д.).

Символика круга в различных религиях сопоставляется с целостностью, вечностью и бесконечной мудростью.

Например, в масонских учениях круг как форма без начала и конца — это источник бесконечного времени и пространства, в котором заключена тайна творения.

У буддистов круг символизирует единство внутреннего и внешнего мира.

В дзен-буддизме круг — это символ высшей степени просветления и совершенства. На основе этого представления построены принципы инь и янь (в виде круга, разделенного на две части, — символа взаимодействия и борьбы двух начал).

В христианстве круг служит эталоном божественного и духовного совершенства.

В живой и неживой природе круги и окружности встречаются как на макроуровнях, так и на микроуровнях. Например, движение электронов вокруг атомного ядра; вращение планет вокруг солнца; распространение волн на воде от упавшего груза; образование солнечного и лунного гало; срез дерева; зрачок глаза у человека и многое другое.

Рассмотрим подробней элементы, характерные для окружности.

Радиус окружности— это отрезок, соединяющий центр окружности и любую другую точку, расположенную на линии окружности.

С латинского радиус (radius)- луч, спица колеса. Радиус не сразу приобрел себе такое название.

Слово радиус впервые встречается в 1569 году у французского ученого П. Рамуса, а общепризнанным становится к концу XVII века.

Радиус обозначается маленькой латинской буквой (r) или заглавной (R).

В окружности можно провести столько же радиусов, сколько точек имеет линия окружности; все эти радиусы равны.

Диаметр — это отрезок прямой, проходящий через центр окружности и соединяющий две точки на этой окружности.

Диаметр в переводе с греческого (diametros) — поперечник.

Обычно диаметр обозначают латинской маленькой буквой d или заглавной D.

По величине диаметр равен двум радиусам, лежащим на одной прямой.

d = 2r

Следовательно, радиус- это половина диаметра.

r = d: 2

Пример 1

Радиус окружности равен 6 см.

Чему равен диаметр окружности?

r = 6 см

d — ?

Решение:

d = 2r

d = 2r= 2*6 = 12 (см) диаметр окружности

Ответ: d= 12 см

Пример 2

Диаметр окружности равен 12 см.

Чему равен радиус окружности?

d = 12 см

r — ?

Решение:

r = d : 2

r = 12 : 2 = 6 (см) радиус окружности

Ответ: r = 6 см

У меня есть дополнительная информация к этой части урока!

Секущая окружности — это прямая, пересекающая окружность в двух точках. В результате окружность делится на дуги.

Точки А и В — точки пересечения секущей с окружностью.

Образовались две дуги: (mathbf)

Отрезок, который соединяет любые две точки на окружности (отрезок секущей), называется хордой.

Отрезок АВ (отрезок секущей) на рисунке — хорда окружности.

Хорда в переводе с греческого — струна, тетива.

На рисунке отрезок MN является хордой.

Если хорда проходит через центр окружности, то она является самой большой хордой для этой окружности. По своей сути она является диаметром для данной окружности и делит окружность на две равные дуги.

По мере удаления хорды от центра размеры ее уменьшаются, а дуги делятся на большую и малую.

АВ— самая большая хорда окружности- диаметр окружности.

CD, N₁M_1, NM, FE— хорды окружности.

Хорды окружности, удаленные на равные расстояния от центра, равны.

Хорды NM и N₁M₁ равны.

Если две хорды пересекаются в точке, то их отрезки пропорциональны.

Важно отметить, что все рассмотренные элементы окружности одинаковы и для круга.

Пройти тест и получить оценку можно после входа или регистрации

Видео:Площадь круга. Математика 6 класс.Скачать

Длина окружности и площадь круга

Давайте выясним, что такое длина окружности и как ее определить.

Представьте, что окружность обернута нитью.

Если разрезать эту нить в некоторой точке и размотать ее, то длина нитки будет равна длине окружности.

Обычно длина окружности обозначается заглавной буквой С

Длина окружности (С) зависит от длины ее диаметра (d)

Обратите внимание на рисунок.

Вы можете заметить, что чем больше диаметр, тем больше длина окружности.

Из этого следует, что длина окружности прямо пропорционально зависит от диаметра окружности.

А значит, для любых окружностей отношение длины окружности (С) к длине диаметра (d) является числом постоянным.

Это число (коэффициент пропорциональности) обозначают греческой буквой (mathbf), читается «пи».

С— это длина окружности

d— диаметр окружности

запишем отношение (mathbf)

отсюда следует, что длина окружности равна

Так как диаметр окружности вдвое больше радиуса d = 2r, получим еще одну формулу для вычисления длины окружности

Выясним, чему равна постоянная величина — число (mathbf)

Число (mathbf)- это иррациональное число, т.е. число, которое представлено в виде бесконечной непериодической десятичной дроби.

У меня есть дополнительная информация к этой части урока!

История числа (mathbf) насчитывает около 4 тысячелетий.

Одно из первых доказательств древнего существования этого числа (mathbf) заключено в папирусе Ахмеса, в одном из старейших задачников (1650 год до н.э.), найденного в Древнем Египте.

В папирусе дано достаточно точное, особенного для того времени, значение числа, равного 3,1605.

Точнее число (mathbf) рассчитал древнегреческий математик Архимед. Он приближенно представил значение константы в виде обыкновенной дроби (mathbf<frac >)

Архимеду удалось найти точное приближение числа (mathbf) (т.е. узкий числовой промежуток к которому принадлежит число (mathbf)).

Пройти тест и получить оценку можно после входа или регистрации

Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Решения задач по теме «Длина окружности и площадь круга»

Рассмотрим примеры решения задач

Задача 1

Найдите длину окружности, если ее радиус равен 4 см.

Число (mathbf<>) округлите до сотых.

r = 4 см

Длину окружности С — ?

Решение:

Подставив в формулу известные значения радиуса и постоянной (mathbf), получим:

Ответ: (mathbf)(см)

Задача 2

Длина окружности надувного бассейна 15,7м.

Найдите диаметр этого бассейна.

Число (mathbf) округлите до сотых.

C = 15,7 м

Диаметр d — ?

Решение:

Подставив в формулу известные значения длины окружности и постоянной (mathbf), получим:

Ответ: (mathbf) (м)

Задача 3

Диаметр окружности равен 6 см.

Найдите площадь круга, ограниченного этой окружностью.

Значение числа (mathbf) округлить до сотых.

d = 6 cм

Площадь круга S — ?

Решение:

Подставим в формулу известные значения диаметра окружности и постоянной , получим:

(mathbf<S = frac 3,146^2 = frac <3,1436> > = 3,149=28,26) (cм 2 ) площадь круга

Ответ: (mathbf) (см 2 )

Задача 4

Вычислите площадь полукруга, если радиус круга равен 5 см.

Значение (mathbf) округлить до целых.

r = 5 cм

Площадь полукруга S_п — ?

Решение:

Площадь круга найдем по формуле:

Площадь полукруга будет равна половине площади всего круга.

Следовательно, формула для расчета площади полукруга получится вида:

Подставим в формулу известные значения радиуса круга и постоянной (mathbf), получим:

(mathbf<S_п = frac =37,5>) (cм 2 ) площадь полукруга

Ответ: (mathbf) (см 2 )

Задача 5

Найдите площадь круга, если известна длина окружности С.

Длина окружности С

Площадь круга S — ?

Решение:

Длина окружности выражается формулой:

Выразим неизвестный радиус окружности через длину окружности:

Площадь круга определяем по формуле:

Подставим, полученные выражения для радиуса окружности, в формулу площади круга, получим:

Сократим полученную дробь:

У меня есть дополнительная информация к этой части урока!

Кроме вычислительных задач, существуют задачи на построение окружности и круга.

Окружность и круг можно начертить с помощью чертежного инструмента, который называется циркуль.

В переводе с латинского языка circulus означает «окружность», «круг».

Циркуль использовали еще с древности, много тысяч лет назад, об этом свидетельствуют найденные на раскопках находки, изображения.

Циркуль представляет собой две одинаковые по длине «ножки». На конце одной из них игла, а на второй- грифель.

Есть циркуль, у которого вместо «ножки» с грифелем помещается карандаш.

Рассмотрим, как построить окружность (круг) на бумаге с помощью циркуля и линейки.

Если задан радиус окружности (круга), то в нулевую отметку на линейке ставим иголку циркуля, другая «ножка» циркуля с грифелем в точку на линейке, равной по значению заданному радиусу.

Ставим точку на листе бумаги — это будет центр окружности (круга), в эту точку ставим иголку циркуля.

Не отрывая грифеля второй «ножки» циркуля от бумаги проводим окружность с заданным радиусом.

Если в задаче задан диаметр, то, прежде чем совершать замер по линейке, необходимо диаметр разделить пополам.

Таким образом, устанавливаем раствор циркуля по линейке на расстояние d:2 = r и чертим окружность по выше изложенной схеме.

Чтобы начертить окружность на местности, пользуются колышком и веревкой. Колышек вбивают в землю — предполагаемый центр окружности; веревка одним концом закрепляется к этому колышку, второй конец веревки туго натягивается; далее очерчивают окружность.

Данный способ построения окружности (круга) может быть применен и на бумаге, если под рукой не оказалось циркуля.

В качестве колышка берется кнопка, к ней привязывается нить определенной длинны (длина нити равна значению заданного радиуса), ко второму концу привязывается карандаш

Пройти тест и получить оценку можно после входа или регистрации

Видео:Математика 6 класс (Урок№76 - Длина окружности. Площадь круга.)Скачать

Формулы для длины окружности и площади круга и пример их использования

Окружность и круг — две совершенные плоские фигуры, свойства которых изучают в обязательном порядке в любом школьном курсе геометрии. В этой статье мы рассмотрим, как находить длину окружности и площадь круга, используя простые математические формулы.

Видео:Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

В чем разница между окружностью и кругом?

Прежде чем переходить к рассмотрению формул длины окружности и площади круга, следует привести определения этих фигур.

В геометрии под окружностью понимают совокупность точек на плоскости, которые находятся от фиксированной точки на одинаковом расстоянии R. В свою очередь, круг — это набор точек плоскости, которые от заданной точки расположены на расстояниях, равных или меньших, чем некоторое число R. Иными словами, окружность представляет собой одну единственную кривую линию, а круг занимает некоторую площадь. Окружность — это «обод» круга.

Вам будет интересно: Династия Шан: основоположник, исторические факты

Именно поэтому, вопрос, как находить площадь окружности, считается некорректно поставленным. Окружность (единственная линия) не имеет площади, однако имеет длину. Для круга же разговор о площади имеет смысл, кроме того, также можно говорить и о длине окружности, которая его ограничивает.

Видео:Длина окружности. Математика 6 класс.Скачать

Основные свойства рассматриваемых фигур

Окружность и круг обладают рядом общих характеристик, которые кратко перечислим ниже:

Поворот на произвольный угол круга или окружности вокруг оси, проходящей через его/ее центр и перпендикулярной плоскости фигуры, является операцией симметрии.

Видео:Длина окружности и площадь кругаСкачать

Формулы для длины окружности и площади круга

Познакомившись с понятием и основными свойствами рассматриваемых плоских фигур, можно перейти к количественному определению их размеров. Длина окружности и площадь круга вычисляются по следующим двум формулам:

Из этих формул следует, что величина R — радиус — полностью характеризует свойства обеих фигур. Величина L измеряется в метрах (

R), а S — в метрах квадратных (

В формулах символ π представляет некоторую константу, которая является иррациональным числом (ее нельзя вычислить точно). С точностью до 4 знаков после запятой число π равно 3,1416. Отметим, что при выполнении расчетов эта константа может быть заменена дробью 201/64. Если вычислить значение этой дроби, то получится число 3,1406, которое всего на 0,03 % отличается от истинной константы.

Заметим, что формула для длины окружности справедлива также для определения аналогичной характеристики круга.

Указанные формулы могут быть переписаны через диаметр, учитывая, что D = 2 * R, получаем:

Видео:Длина окружности. Площадь круга, 6 классСкачать

Использование рассмотренных формул для решения задачи

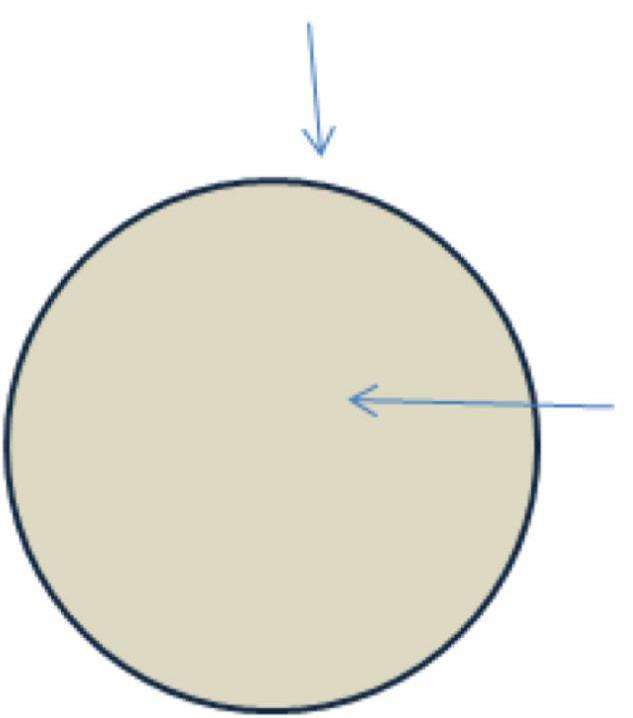
Формулы для площади круга и длины окружности используем для решения задач. Например, у Маши имеется кусок ткани прямоугольной формы, размеры которой равны 5 x 4 метра. Необходимо определить, какого максимального размера круг она сможет вырезать из этой ткани.

Смысл этой задачи состоит в определении размера круга, вписанного в четырехугольник. Эта ситуация изображена на рисунке ниже.

Из рисунка можно заметить, что диаметр вписанного круга D будет равен длине наименьшей стороны четырехугольника, в данном случае D = 4 метра. Зная диаметр, можно непосредственно применить формулы, которые записаны для длины и площади этой фигуры в предыдущем пункте статьи. Имеем:

1. L = π * D = 3,1416 * 4 = 12,5664 м.

2. S = π * D²/4 = 3,1416 * 4²/4 = 12,5664 м².

Мы получили любопытный результат: площадь круга равна точно такой же величине, что и длина его окружности, но единицы измерения являются разными для них. Этот результат является простым совпадением, поскольку D=4 — это единственное число, для которого абсолютные значения L и S равны.

📸 Видео

6 класс, 3 урок, Длина окружности и площадь кругаСкачать

Длина окружности и площадь круга | Математика 6 класс #24 | ИнфоурокСкачать

Окружность и круг. Центр, радиус, диаметр, хорда, дуга, сектор и длина окружности, площадь круга.Скачать

Чем отличается круг от окружностиСкачать

КАК НАЙТИ ПЛОЩАДЬ КРУГА, ЕСЛИ ИЗВЕСТЕН ДИАМЕТР? Примеры | МАТЕМАТИКА 6 классСкачать

ДЛИНА ОКРУЖНОСТИ и ПЛОЩАДЬ КРУГА 9 класс геометрия АтанасянСкачать

Длина окружности. Площадь круга.Скачать

ГЕОМЕТРИЯ 9 класс: Длина окружности, площадь круга и площадь кругового сектораСкачать

МАТЕМАТИКА 6 класс: Длина окружности и площадь круга | ВидеоурокСкачать

5 класс, 22 урок, Окружность и кругСкачать