Многоугольник называется описанным около окружности если ответ

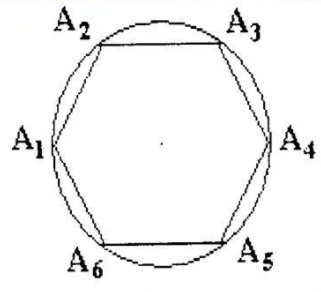
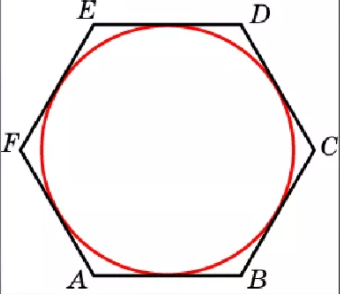
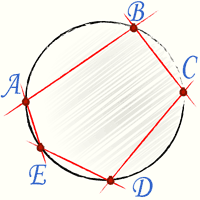
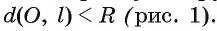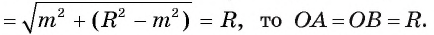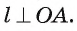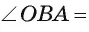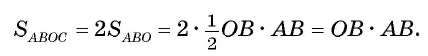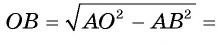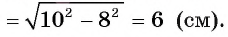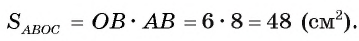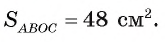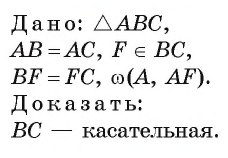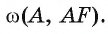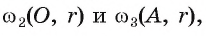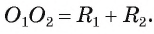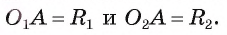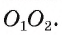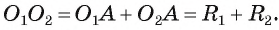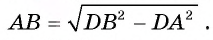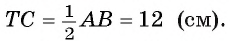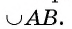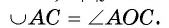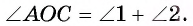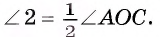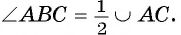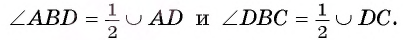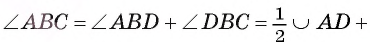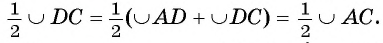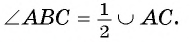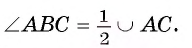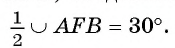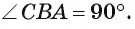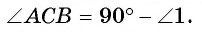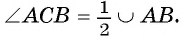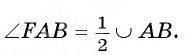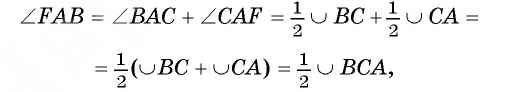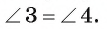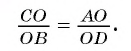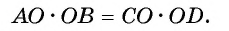Вписанным в круг многоугольником называется такой многоугольник, вершины которого лежат на окружности. Описанным около круга многоугольником называется такой многоугольник, стороны которого касаются окружности.

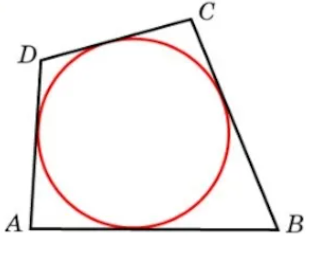
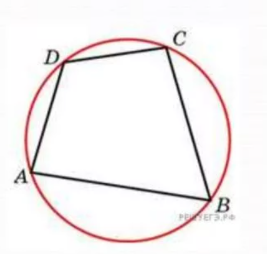
Описанной около многоугольника окружностью называется окружность, проходящая через его вершины. Вписанной в многоугольник окружностью называется окружность, касающаяся его сторон.

Вписанный многоугольник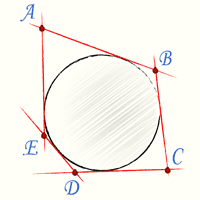

Описанный многоугольник

Если многоугольник взят произвольно, то в него нельзя вписать и около него нельзя описать окружность. Только многоугольники соответствующие некоторым правилам можно описать окружностью или вписать в них окружность.

Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Правила для многоугольников которые можно вписать в окружность и описать окружность вокруг них

Для треугольника всегда возможны и вписанная окружность и описанная окружность.

Для четырехугольника окружность можно вписать только в том случае, если суммы его противоположных сторон одинаковы. Из всех параллелограммов только в ромб и квадрат можно вписать окружность. Ее центр лежит на пересечении диагоналей.

Вокруг четырехугольника окружность можно описать только если сумма противоположных углов равна 180°. Из всех параллелограммов только около прямоугольника и квадрата можно описать окружность. Ее центр лежит на пересечении диагоналей.

Вокруг трапеции возможно описать окружность или в трапецию можно вписать окружность если трапеция равнобокая.

Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Какой многоугольник называется описанным около окружности если

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Вписанные и описанные многоугольники

Вписанным в круг многоугольником называется такой многоугольник, вершины которого лежат на окружности. Описанным около круга многоугольником называется такой многоугольник, стороны которого касаются окружности.

Описанной около многоугольника окружностью называется окружность, проходящая через его вершины. Вписанной в многоугольник окружностью называется окружность, касающаяся его сторон.

Вписанный многоугольник

Описанный многоугольник

Если многоугольник взят произвольно, то в него нельзя вписать и около него нельзя описать окружность. Только многоугольники соответствующие некоторым правилам можно описать окружностью или вписать в них окружность.

Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Правила для многоугольников которые можно вписать в окружность и описать окружность вокруг них

Для треугольника всегда возможны и вписанная окружность и описанная окружность.

Для четырехугольника окружность можно вписать только в том случае, если суммы его противоположных сторон одинаковы. Из всех параллелограммов только в ромб и квадрат можно вписать окружность. Ее центр лежит на пересечении диагоналей.

Вокруг четырехугольника окружность можно описать только если сумма противоположных углов равна 180°. Из всех параллелограммов только около прямоугольника и квадрата можно описать окружность. Ее центр лежит на пересечении диагоналей.

Вокруг трапеции возможно описать окружность или в трапецию можно вписать окружность если трапеция равнобокая.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Многоугольники, описанные около окружности Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности. Сама окружность. — презентация

Презентация была опубликована 6 лет назад пользователемМаксим Шишов

Похожие презентации

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Презентация на тему: » Многоугольники, описанные около окружности Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности. Сама окружность.» — Транскрипт:

1 Многоугольники, описанные около окружности Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности. Сама окружность при этом называется вписанной в многоугольник.

2 Теорема 1 В любой треугольник можно вписать окружность. Ее центром будет точка пересечения биссектрис этого треугольника.

3 Теорема 2 В любой правильный многоугольник можно вписать окружность. Ее центром является точка пересечения биссектрис углов многоугольника.

4 Теорема 3 В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны, т.е. AB + CD = AD + BC.

5 Вопрос 1 Какой многоугольник называется описанным около окружности? Ответ: Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности.

6 Вопрос 2 Какая окружность называется вписанной в многоугольник? Ответ: Вписанной в многоугольник называется окружность, касающаяся всех сторон этого многоугольника.

7 Вопрос 3 Во всякий ли треугольник можно вписать окружность? Ответ: Да.

8 Вопрос 4 Какая точка является центром вписанной в треугольник окружности? Ответ: Центром вписанной окружности является точка пересечения биссектрис этого треугольника.

9 Вопрос 5 В любой ли правильный многоугольник можно ли вписать окружность? Ответ: Да.

10 Вопрос 6 Можно ли вписать окружность в: а) остроугольный треугольник; б) прямоугольный треугольник; в) тупоугольный треугольник? Ответ: а) Да; б) да; в) да.

11 Вопрос 7 Может ли центр вписанной в треугольник окружности находиться вне этого треугольника? Ответ: Нет.

12 Вопрос 8 Какой вид имеет треугольник, если: а) центры вписанной и описанной около треугольника окружностей совпадают; б) центр вписанной в него окружности принадлежит одной из его высот? Ответ: а) Равносторонний; б) равнобедренный.

13 Упражнение 1 Укажите центр окружности, вписанной в квадрат ABCD. Ответ:

14 Упражнение 2 Укажите центр окружности, вписанной в квадрат ABCD. Ответ:

15 Упражнение 3 Укажите центр окружности, вписанной в ромб ABCD. Ответ:

16 Упражнение 4 Укажите центр окружности, вписанной в треугольник ABC. Ответ:

17 Упражнение 5 Укажите центр окружности, вписанной в треугольник ABC. Ответ:

18 Упражнение 6 Ответ: 2. Найдите радиус окружности, вписанной в квадрат со стороной 4.

19 Упражнение 7 Ответ: 6. Найдите сторону квадрата, описанного около окружности радиуса 3.

20 Упражнение 8 Ответ: 10. Найдите высоту трапеции, в которую вписана окружность радиуса 5.

21 Упражнение 9 Окружность, вписанная в треугольник ABC, делит сторону AB в точке касания D на два отрезка AD = 5 см и DB = 6 см. Найдите периметр треугольника ABC, если известно, что BC = 10 см. Ответ: 30 см.

22 Упражнение 10 Ответ: 20 см. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, которые равны 4 см и 3 см, считая от вершины. Найдите периметр треугольника.

23 Упражнение 11 К окружности, вписанной в треугольник АВС, проведены три касательные. Периметры отсеченных треугольников равны p 1, p 2, p 3. Найдите периметр данного треугольника. Ответ: p 1 + p 2 + p 3.

24 Упражнение 12 Ответ: 34 см. В равнобедренном треугольнике боковые стороны делятся точками касания вписанной в треугольник окружности в отношении 7:5, считая от вершины, противоположной основанию. Найдите периметр треугольника, если его основание равно 10 см.

25 Упражнение 13 Ответ: а) Нет; Всегда ли можно ли вписать окружность в: а) прямоугольник; б) параллелограмм; в) ромб; г) квадрат; д) дельтоид ? б) нет; в) да; г) да; д) да.

26 Упражнение 14 Два равнобедренных треугольника имеют общее основание и расположены по разные стороны от него. Можно ли в образованный ими выпуклый четырехугольник вписать окружность? Ответ: Да.

27 Упражнение 15 Можно ли вписать окружность в четырехугольник, стороны которого последовательно равны 1, 2, 3, 4? Ответ: Нет.

28 Упражнение 16 Какой вид имеет четырехугольник, если центр вписанной в него окружности совпадает с точкой пересечения диагоналей? Ответ: Ромб.

29 Упражнение 17 Около окружности описана трапеция, периметр которой равен 18 см. Найдите ее среднюю линию. Ответ: 4,5 см.

30 Упражнение 18 В трапецию, периметр которой равен 56 см, вписана окружность. Три последовательные стороны трапеции относятся как 2:7:12. Найдите стороны трапеции. Ответ: 4 см, 14 см, 24 см, 14 см.

31 Упражнение 19 Боковые стороны трапеции, описанной около окружности, равны 2 см и 4 см. Найдите среднюю линию трапеции. Ответ: 3 см.

32 Упражнение 20 Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности. Ответ: 2.

33 Упражнение 21 Докажите, что если в трапецию ABCD (AB||CD) вписана окружность с центром O, то углы AOD и BOC равны 90 о. Доказательство. Лучи AO и DO являются биссектрисами внутренних односторонних углов при параллельных прямых AB и CD. Следовательно, угол AOD равен 90 о. Аналогично, угол BOC равен 90 о.

34 Упражнение 22 Докажите, что если в равнобедренную трапецию ABCD (AB||CD) вписана окружность, ее боковые стороны AD и BC равны средней линии EF. Доказательство. Сумма боковых сторон трапеции равна сумме оснований. Следовательно, боковая сторона равна полусумме оснований, т.е. равна средней линии.

35 Упражнение 23 Три последовательные стороны четырехугольника, в который можно вписать окружность, равны 6 см, 8 см и 9 см. Найдите четвертую сторону и периметр этого четырехугольника. Ответ: 7 см, 30 см.

36 Упражнение 24 Противоположные стороны четырехугольника, описанного около окружности, равны 7 см и 10 см. Можно ли по этим данным найти периметр четырехугольника? Ответ: Да, 34 см.

37 Упражнение 25 Периметр четырехугольника, описанного около окружности, равен 24, две его стороны равны 5 и 6. Найдите большую из оставшихся сторон. Ответ: 7.

38 Упражнение 26 К окружности, вписанной в треугольник АВС, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника. Ответ: 24.

39 Упражнение 27 В шестиугольнике ABCDEF, описанном около окружности AB = 3, CD = 4, EF = 2. Найдите периметр этого шестиугольника. Ответ: 18.

40 Упражнение 28* Можно ли вписать окружность в пятиугольник, стороны которого последовательно равны 1, 2, 1, 2, 1? Ответ: Нет. Если в пятиугольник можно вписать окружность, то сумма любых двух его не соседних сторон меньше суммы трех оставшихся сторон.

41 Упражнение 29* Можно ли вписать окружность в шестиугольник, стороны которого последовательно равны 1, 2, 1, 2, 1, 2? Ответ: Нет. Если в шестиугольник можно вписать окружность, то сумма любых трех его не соседних сторон равна сумме трех оставшихся сторон.

42 Упражнение 30* Стороны пятиугольника, описанного около окружности, последовательно равны 1, 2, 3, 2, 1. Найдите радиус этой окружности, если угол, заключенный между сторонами, равными 1, равен 120 о. Ответ:

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Описанная и вписанная окружность

теория по математике 📈 планиметрия

Видео:110. Окружность, описанная около правильного многоугольникаСкачать

Описанная окружность

Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.

Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.

Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Вписанная окружность

Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.

В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.

Вписанный и описанный треугольники

Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.

В любой треугольник можно вписать окружность: 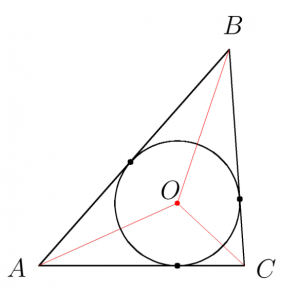Центр вписанной окружности

Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.

Вписанный и описанный четырехугольники

Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.

Условие вписанной в 4-х угольник окружности

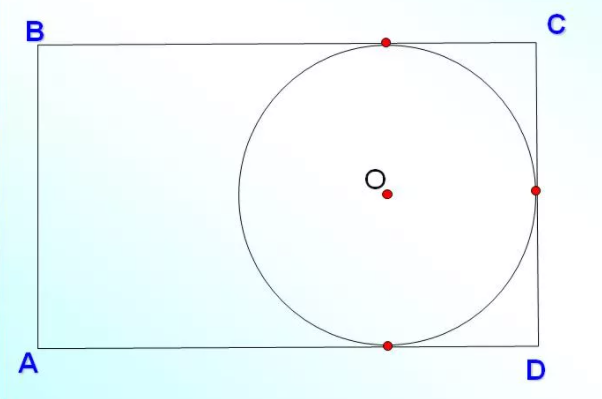
Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.

На рисунке выполняется данное условие, то есть AD + BC=DC + AB

Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.

На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.

Видео:Многоугольники. Вписанные и описанные около окружности - геометрия 8 классСкачать

Вписанные и описанные многоугольники — формулы, свойства и примеры с решением

Содержание:

Рассмотрим вопрос о взаимном расположении прямой и окружности. Ранее уже отмечалось, что возможны три случая взаимного расположения прямой и окружности:

1. прямая имеет только две общие точки с окружностью;
2. прямая имеет только одну общую точку с окружностью;
3. прямая не имеет общих точек с окружностью.

Если прямая имеет две общие точки с окружностью, то она называется секущей.

Видео:9 класс. Правильный многоугольник, вписанный в окружность и описанный около окружностиСкачать

Понятие о вписанных и описанных многоугольниках

Взаимное расположение окружности со (О, R) с центром в точке О радиуса R и прямой I характеризуется соотношением между расстоянием d(0, I) от центра О окружности до прямой I и радиусом R окружности. Докажем это.

1) Прямая I имеет только две общие точки с окружностью, если расстояние от центра окружности до прямой I меньше радиуса окружности, т. е.

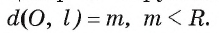
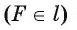
Пусть прямая I не проходит через центр О окружности и расстояние . Обозначим OF — перпендикуляр, проведенный из точки О к прямой I, тогда OF = m. Пусть точки А и В лежат на прямой I

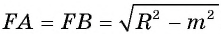
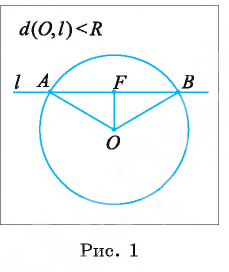
так, что . Докажем, что точки А и В принадлежат окружности.

Действительно, так как по теореме Пифагора

Таким образом, точки А и В — общие точки прямой и окружности. Докажем, что других общих точек прямая I и окружность 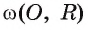не имеют.

Предположим, что существует еще одна точка X — общая для окружности и прямой. Тогда центр окружности О равноудален от точек А, В, и X, а значит, он лежит на серединных перпендикулярах к отрезкам АВ и ВХ, т. е. О — точка перессечения серединных перпендикуляров. Но так как,. Получили противоречие. Значит, наше предположение не верно и других общих точек прямой и окружности нет.

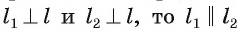
Если прямая I проходит через центр О окружности, т. е. d(0, Z) = 0, то она пересекает окружность в двух точках, которые являются концами диаметра, лежащего на этой прямой.

2) Прямая I имеет только одну общую точку с окружностью, если расстояние от центра окружности до прямой I равно радиусу окружности, т. е. если d(0, I) = R.

Пусть расстояние от центра окружности до прямой I равно радиусу окружности, а точка F — основание перпендикуляра, проведенного из центра окружности к прямой I (рис. 2). Тогда OF = R, а значит, точка F лежит на окружности. Других общих точек прямая и окружность не имеют. Действительно, для любой точки X прямой I, не совпадающей с точкой F, выполняется условие ОХ > OF, OF = R, так; как наклонная ОХ больше перпендикуляра OF.

Следовательно, точка X не лежит на окружности.

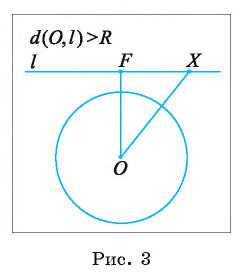
3) Прямая I не имеет общих точек с окружностью, если расстояние от центра О окружности до прямой I больше радиуса окружности, т. е. если d(0, I) > R.

Пусть расстояние от центра О окружности до прямой I больше радиуса R. Обозначим буквой F основание перпендикуляра, проведенного из центра О окружности к прямой I (рис. 3). Тогда OF = d(0, I), d(0, I) > R.

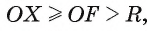
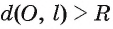
Для любой точки X прямой выполняется условие , следовательно, точка X не лежит на окружности. Таким образом, в случае прямая и окружность не имеют общих точек.

Касательная к окружности

Рассмотрим случай, когда прямая и окружность имеют единственную общую точку. Прямая, имеющая единственную общую точку с окружностью, имеет специальное название — касательная.

Определение. Касательной к окружности называется прямая, которая имеет с окружностью только одну общую точку.

Единственная общая точка прямой и окружности называется точкой касания прямой и окружности.

Если прямая I имеет единственную общую точку А с окружностью, то говорят, что прямая I касается окружности в точке А.

Теорема 1 (о свойстве касательной). Касательная к окружности перпендикулярна радиусу этой окружности, проведенному в точку касания.

1) Пусть прямая I касается окружности 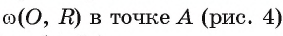Докажем, что

2) Предположим, что это не так. Тогда радиус ОА является наклонной к прямой I. Перпендикуляр, проведенный из точки О к прямой I, меньше наклонной ОА, следовательно, расстояние от центра окружности до прямой

меньше радиуса. Значит, прямая и окружность имеют две общие точки, что противоречит условию. Таким образом, прямая I перпендикулярна радиусу ОА.

Рассмотрим следствия из данной теоремы.

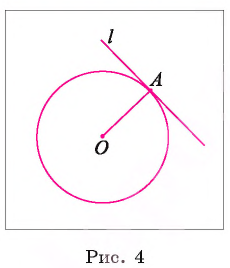
Пусть через точку А проведены две прямые, касающиеся окружности 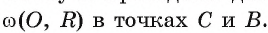Тогда отрезки АВ и АС называются отрезками касательных, проведенными из точки А (рис. 5).

Следствие 1. Отрезки касательных к окружности, проведенные из одной точки, равны.

1) Пусть АВ и АС — отрезки касательных, проведенные из точки А (рис. 5). Для доказательства равенства АВ = АС рассмотрим треугольники АВО и АСО.

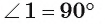
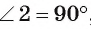
2) По свойству касательной и , т. е. треугольники АВО и АСО — прямоугольные.

3), так как АО — общая гипотенуза, а катеты О В и ОС равны как радиусы окружности. Отсюда следует, что АВ =АС.

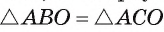
Следствие 1 доказано.

Из равенства треугольников АВО и АСО вытекает также, что 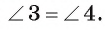. Таким образом, получим еще одно следствие.

Следствие 2. Отрезки касательных к окружности, проведенные из одной точки, составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Теперь докажем признак, который позволяет устанавливать, в каком случае прямая касается окружности. Оказывается, для этого достаточно установить, что прямая перпендикулярна радиусу и проходит через его конец, лежащий на окружности.

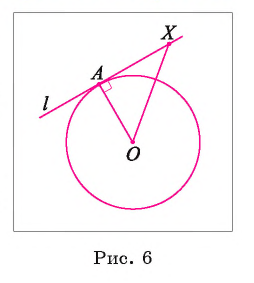
Теорема 2 (признак касательной). Если прямая перпендикулярна радиусу окружности и проходит через его конец, лежащий на окружности, то она касается этой окружности.

1) Пусть прямая I проходит через точку А окружности и перпендикулярна радиусу О А (рис. 6). Для доказательства того, что прямая I касается окружности, достаточно доказать, что она имеет с этой окружностью единственную общую точку.

2) Так как точка А лежит на окружности и прямая I проходит через точку А, то А — общая точка прямой I и окружности.

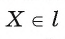
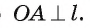
3) Других общих точек прямая I и окружность не имеют. Действительно, для любой точки отрезок ОХ является наклонной, так как по условию Следовательно, ОХ > ОА, т. е. точка X не принадлежит окружности.

Таким образом, точка А — единственная общая точка прямой I и окружности, а, значит, прямая I — касательная к окружности.

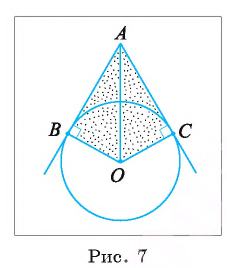
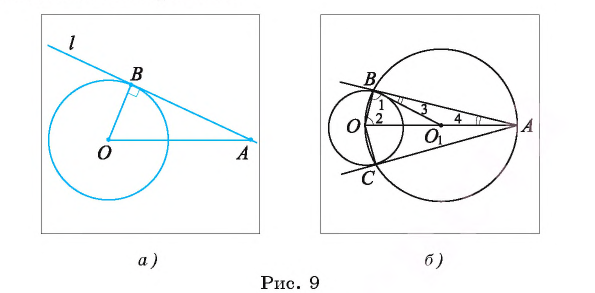
Пример №1

Через точку А, находящуюся от центра О окружности на расстоянии 10 см, проведены две касательные АВ и АС, где Б и С — точки касания. Вычислите площадь 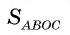четырехугольника АВОС, если АВ + АС = = 16 см ( рис. 7).

Решение:

1) Площадь четырехугольника АВОС равна сумме площадей треугольников АВО и АСО.

2) По свойству касательной 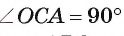. Прямоугольные треугольники АВО и АСО равны по гипотенузе и катету (АО — общая, ОВ = ОС). Значит,

3) Отрезки касательных к окружности, проведенные из одной точки, равны. Следовательно, АВ=АС = 8 см. Теперь, применив теорему Пифагора, вычислим

Таким образом,

Ответ:

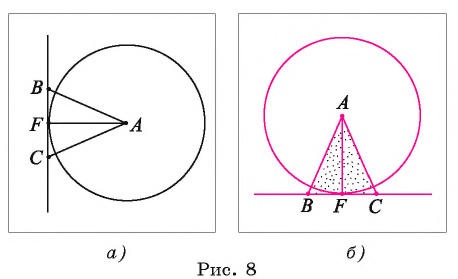
Пример №2

Точка F — середина основания ВС равнобедренного треугольника АБС. Докажите, что прямая ВС является касательной к окружности 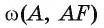(рис. 8, а, б).

Доказательство.

1) Прямая ВС проходит через конец F радиуса окружности 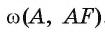. Для доказательства того, что ВС является касательной, достаточно доказать, что

2) В равнобедренном треугольнике AВС отрезок AF — медиана, проведенная к его основанию. Следовательно, 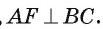Таким образом, по признаку касательной прямая ВС касается окружности

Что и требовалось доказать.

Пример №3

Точка А лежит вне окружности 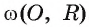Постройте прямую, которая касается окружности и проходит через точку А.

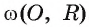
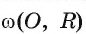
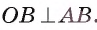
1) Пусть прямая I, проходящая через точку А и касающаяся окружности , построена. Точка В — точка касания. Тогда по свойству касательной OB LAB (рис. 9, а). Следовательно, для построения искомой касательной необходимо построить точку В на окружности так, что .

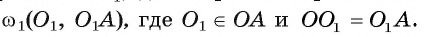
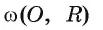
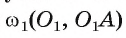
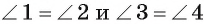
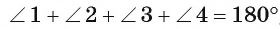
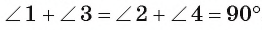
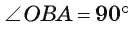
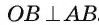
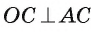
2) Рассмотрим окружность coj, диаметром которой является отрезок АО, т. е. Пусть В и С — точки пересечения окружностей и (рис. 9, б). Заметим, что , как углы при основании равнобедренных треугольников ВО,О и ВО,А соответственно. Так как , то Значит, , т. е.. Аналогично доказывается, что. Отсюда по признаку

касательной к окружности следует, что прямые АВ и АС являются касательными. Теперь понятна последовательность необходимых построений.

1) Проводим отрезок О А, соединяющий центр О данной окружности и точку А (рис. 10, а).

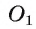
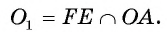
2) Строим середину отрезка ОА: Точки F и Е — точки пересечения окружностей

где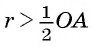(рис. 10, б).

3) Строим окружность 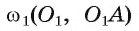(рис. 10, в) и точки Б, С — точки пересечения данной и построенной окружностей.

4) Прямые АВ и АС — искомые касательные к данной окружности.

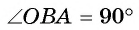
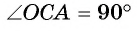
Доказательство. По построению и (см. задачу № 251 учебного пособия «Геометрия, 7»), т. е. АВ1ОВ и АС 1ОВ. Следовательно, по признаку касательной АВ и АС — касательные.

Взаимное расположение двух окружностей

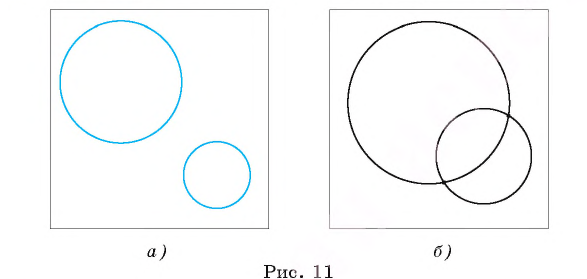
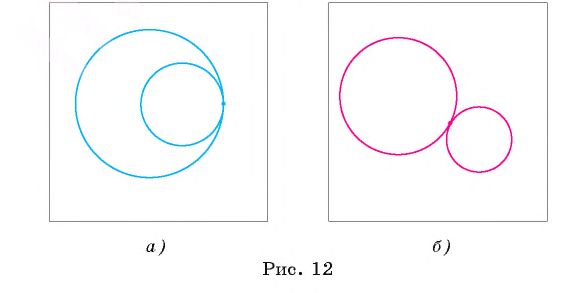
Рассмотрим вопрос о взаимном расположении двух окружностей в плоскости. Возможны следующие случаи взаимного расположения двух различных окружностей:

1) окружности не имеют общих точек (в этом случае говорят, что они не пересекаются (рис. 11, а ));

2) окружности имеют две общие точки (в этом случае говорят, что окружности пересекаются (рис. 11, б));

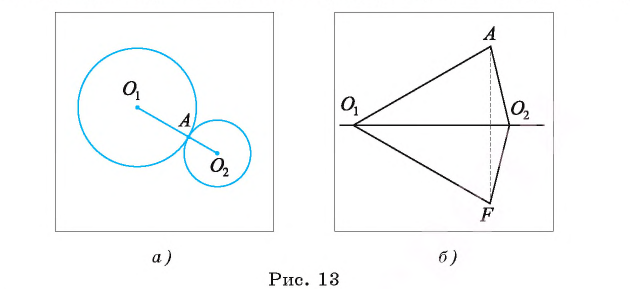
3) окружности имеют только одну общую точку, и одна из окружностей лежит внутри круга, ограниченного другой окружностью (в этом случае говорят, что они касаются внутренним образом (рис. 12, а ));

4) окружности имеют только одну общую точку, и ни одна из окружностей не лежит внутри круга, ограниченного другой окружностью (в этом случае говорят, что они касаются внешним образом, (рис. 12, б)).

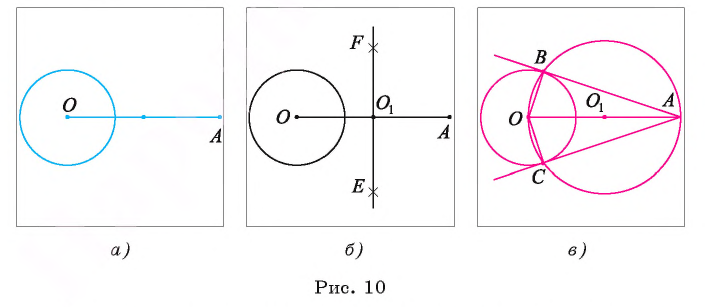
Пример №4

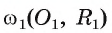
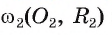
Докажите, что если две окружности и касаются внешним образом, то расстояние между их центрами равно сумме их радиусов, т. е.

Доказательство.

1) Пусть окружности 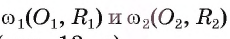касаются внешним образом в точке А (рис. 13, а).

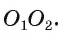
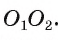
2) Докажем, что точка А лежит на отрезке Допустим, что точка А не лежит на отрезке Заметим, что в случае внешнего касания точка А не может лежать на продолжении отрезка Пусть точка касания А не лежит на отрезке (рис. 13, б). Тогда

3) Пусть F — точка, симметричная точке А относительно прямой . Тогда , а значит, точка F принадлежит каждой окружности. Таким образом, окружности имеют две общие точки А и F, что противоречит условию их касания. Следовательно, точка касания А лежит на отрезке

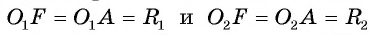
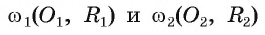
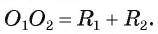
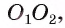
4) Докажем, что Точка А лежит на отрезке значит,

Справедливо и обратное утверждение.

Пример №5

Докажите, если расстояние между центрами двух окружностей, лежащих в плоскости, равно сумме их радиусов, то такие окружности касаются внешним образом.

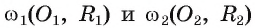
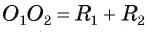
1) Пусть даны две окружности и известно, что Докажем, что окружности касаются внешним образом.

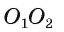
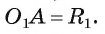
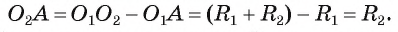
2) На отрезкерассмотрим точку А такую, что Тогда . Таким образом, точка А принадлежит каждой из данных окружностей.

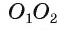
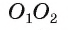
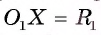
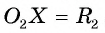
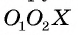
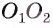
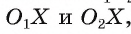
3) Докажем, что окружности не имеют других общих точек. Действительно, на прямой таких точек нет. Предположим, что существует точка X вне прямой принадлежащая каждой окружности. Тогда и В треугольнике длина стороныравна сумме длин сторон , что невозможно.

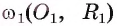
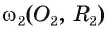
4) Таким образом, предположение о существовании еще одной точки, принадлежащей окружностям и , приводит к противоречию. Следовательно, других общих точек, кроме точки А, не существует, т. е. окружности касаются.

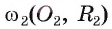
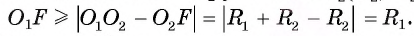
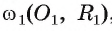
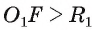
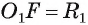
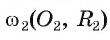
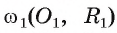
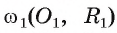
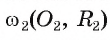
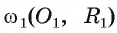
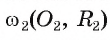
5) Докажем, что окружности касаются внешним образом. Для любой точки F окружностивыполняется условие Таким образом, либо точка F лежит вне окружности когда , либо эта точка принадлежит обеим окружностям, если Но в этом случае точка F есть точка А касания окружностей. Следовательно, окружность расположена вне части плоскости, ограниченной окружностью . Аналогично можно доказать, что окружность расположена вне части плоскости, ограниченной окружностью . Теперь доказано, что окружности и касаются внешним образом.

Пример №6

Докажите, что две окружности касаются внутренним образом тогда и только тогда, когда расстояние между их центрами равно модулю разности их радиусов.

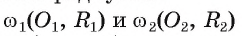
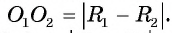
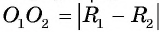
Другими словами, если окружности касаются внутренним образом, то И наоборот, если выполняется равенство , то окружности касаются внутренним образом.

Пример №7

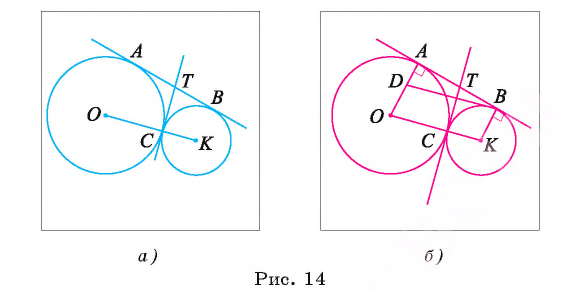
Две окружности с центрами в точках О и К, радиусы которых равны 16 см и 9 см соответственно, касаются внешним образом в точке С. К окружностям проведена общая касательная АВ, где точки А и В — точки касания.

Общая касательная, проведенная через точку С, пересекает касательную АВ в точке Т (рис. 14, а). Вычислите длину отрезка СТ.

Решение:

Для решения задачи воспользуемся тем, что отрезки касательных, проведенные к окружности из одной точки, равны, а радиусы, проведенные в точку касания, перпендикулярны касательной. Учтем также, что окружности касаются внешним образом, а значит, расстояние между их центрами равно сумме их радиусов.

1) Так как отрезки касательных к окружности, проведенные из одной точки, равны, то ТС = ТА = ТВ, т. е. 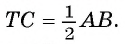. Значит, нам необходимо вычислить длину отрезка АВ.

2) Так как окружности касаются внешним образом, то ОК = ОС + СК = 16 + 9 = 25 (см).

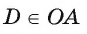
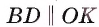
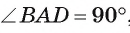
3) Рассмотрим четырехугольник ODBK. Пусть и (рис. 14, б). Так как радиус, проведенный в точку касания, перпендикулярен касательной, то, т. е. треугольник BAD — прямоугольный. Следовательно,

4) Четырехугольник ODBK — параллелограмм, так как его противолежащие стороны параллельны, значит, DB = ОК = = 25 см. Кроме того, DA = ОА — OD = ОА — КВ =16-9 = 7 (см).

Тогда 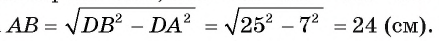Следовательно,

Ответ: ТС = 12 см.

Центральные и вписанные углы

В данном параграфе изучим понятия центрального и вписанного углов.

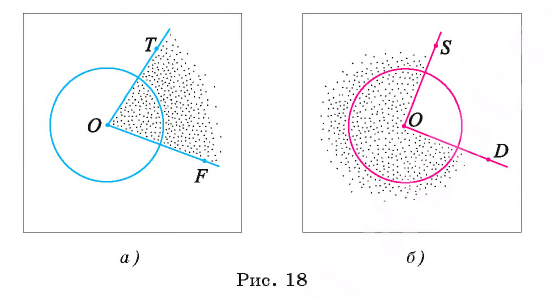
Определение. Центральным углом окружности называется угол с вершиной в центре этой окружности.

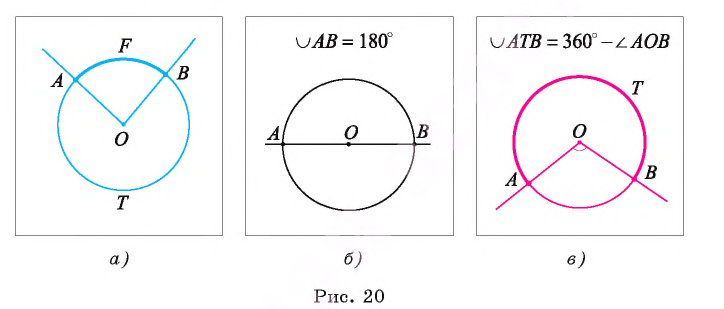
Например, на рисунке 18, а изображен центральный угол TOF, который меньше развернутого угла, а на рисунке 18, б — центральный угол SOD — больше развернутого угла.

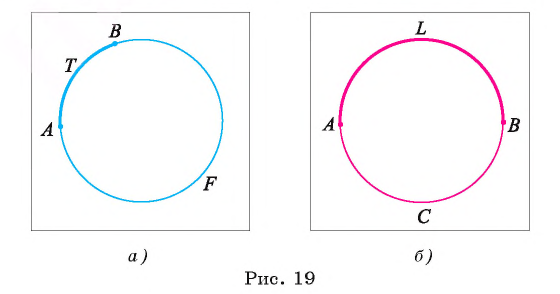
Любые две различные точки А и В окружности служат концами двух дуг. Для различия этих дуг на каждой из них отмечается некоторая промежуточная точка. Например, если на дугах отмечены точки F и Т, то в этом случае дуги обозначаются 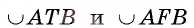и данная запись читается так: «дуга АТВ и дуга AFB» (рис. 19, а). Если понятно, о какой из двух дуг идет речь, употребляется также обозначение

Дуга АВ окружности называется полуокружностью, если ее концы служат концами диаметра этой окружности.

Например, на рисунке 19, б изображены полуокружности ALB и АС В.

Пусть точки А и Б не являются концами диаметра окружности с центром в точке О. Тогда лучи ОА и ОБ служат сторонами двух центральных углов, один из которых меньше, а другой больше развернутого угла (рис. 20, а).

Дуга АВ окружности 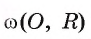и центральный угол АОВ, внутри которого лежит эта дуга, называются соответствующими.

Если дуга окружности лежит внутри соответствующего ей центрального угла, который меньше развернутого угла, то говорят, что эта дуга меньше полуокружности.

Если дуга окружности лежит внутри соответствующего ей центрального угла, который больше развернутого угла, то говорят, что дуга больше полуокружности.

Например, на рисунке 20, а изображены дуга AFB, которая меньше полуокружности, и дуга АТВ — больше полуокружности.

Для сравнения дуг окружности вводится понятие градусной меры дуги окружности.

Дадим определение градусной меры дуги окружности.

Определение. Градусной мерой дуги окружности называется градусная мера соответствующего ей центрального угла.

Градусная мера дуги АВ, как и сама дуга, обозначается

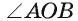
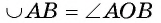
Таким образом, если дуга АВ окружности меньше полуокружности, a — соответствующий ей центральный угол, то (см. рис. 20, а).

Если дуга АВ является полуокружностью, то ее градусная мера равна 180° (рис. 20, б).

Градусная мера дуги АТВ, которая больше полуокружности и дополняет дугу АВ, меньшую полуокружности, до окружности, равна 360° 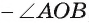, где угол АОВ соответствует дуге АВ (рис. 20, в).

Понятие градусной меры дуги позволяет определить понятие равенства дуг окружности.

Две дуги одной и той же окружности называются равными, если равны их градусные меры.

Если градусная мера дуги АВ равна 33°, то пишут 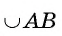= 33°. Читают: «Градусная мера дуги АВ равна 33°», или кратко «Дуга АВ равна 33°».

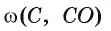
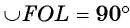
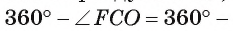
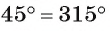
Рассмотрим примеры. Пусть диагонали квадрата ABCD пересекаются в точке О. Окружность пересекает стороны ВС и CD квадрата в точках F и L соответственно. Тогда , а градусная мера дуги FO, которая меньше полуокружности, равна 45°. Градусная мера дуги FLO, которая больше полуокружности, равна (рис. 21, а).

Рассмотрим еще один пример. Пусть точка О — центр окружности, отрезок АВ — хорда окружности, равная ее радиусу, а отрезок АС — диаметр окружности (рис. 21, б).

Тогда градусная мера дуги АВ, которая меньше полуокружности, равна 60°, так как треугольник АОВ — равносторонний, а значит, градусная мера соответствующего ей центрального угла АОВ равна 60°. Градусная мера дуги ВС, которая меньше полуокружности, равна 120°, так как градусная мера соответствующего ей центрального угла ВОС равна 120°.

Можем вычислить градусную меру дуги ВАС, которая больше полуокружности: 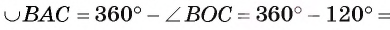= 240°.

Вписанные углы. Рассмотрим понятие вписанного угла

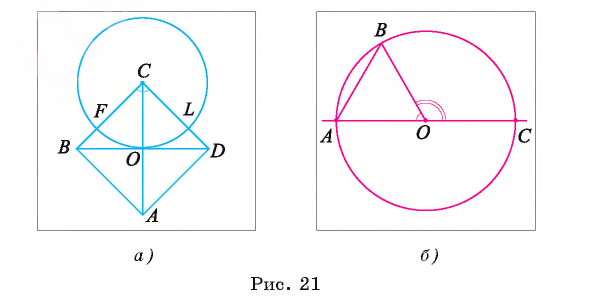
Определение. Угол называется вписанным в окружность, если он меньше развернутого угла, вершина его лежит на окружности, а стороны пересекают эту окружность.

Например, на рисунке 22, а изображен вписанный угол TOF. Если точки А, В и С лежат на окружности, то каждый из угол ABC, ВСА, САВ является вписанным (рис. 22, б).

Пусть 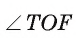— вписанный угол, при этом Г и В — точки пересечения его сторон с окружностью, a TF — дуга, которая лежит внутри этого вписанного угла. В этом случае говорят, что вписанный угол TOF опирается на дугу TF (см. рис. 22, а).

Например, на рисунке 22, в изображены вписанные углы ВАС, ВОС и BFC, которые опираются на одну и ту же дугу ВС.

Теперь докажем теорему о вписанном угле.

Теорема 1(о вписанном угле). Градусная мера вписанного угла равна половине градусной меры, дуги, на которую он опирается.

Пусть вписанный в окружность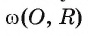угол ABC опирается на дугу АС.

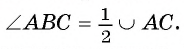
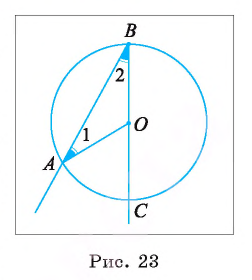
Докажем, что Рассмотрим три возможных случая. Центр О окружности лежит: 1) на одной из сторон угла; 2) во внутренней области угла; 3) во внешней области угла.

Первый случай. Центр О окружности лежит на одной из сторон угла ABC, например на стороне ВС (рис. 23).

1) Дуга АС меньше полуокружности, следовательно,

2) Угол АОС — внешний угол равнобедренного треугольника АОВ, значит,

3) Так как углы при основании равнобедренного треугольника АОВ равны, то

4) Так как 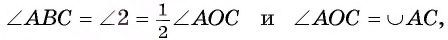, то

Второй случай. Центр О окружности лежит во внутренней области угла.

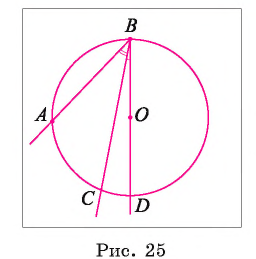
1) Пусть D — точка пересечения луча ВО и дуги АС (рис. 24). Тогда по доказанному в первом случае

Таким образом,

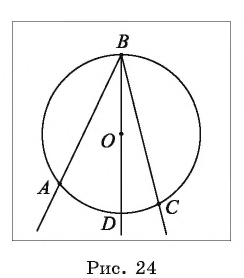
Третий случай. Центр О окружности лежит во внешней области угла ABC.

1) Пусть D — точка пересечения луча ВО с окружностью (рис. 25). Тогда согласно доказанному в первом случае

Таким образом,

Из данной теоремы получим следующие следствия.

Следствие 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис. 26, а).

Следствие 2. Вписанный угол, опирающийся на полуокружность, прямой (рис. 26, б).

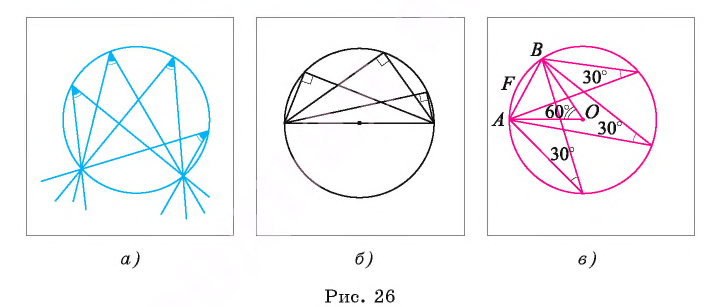
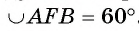
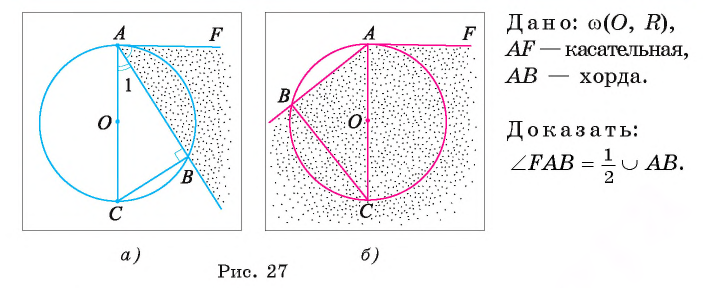
Рассмотрим пример. Пусть хорда АВ соединяет концы дуги AFB и равна радиусу окружности со (О, R). Тогда градусная мера каждого из вписанных углов, опирающихся на дугу AFB, равна 30° (рис. 26, в). Действительно, градусная мера центрального угла АОВ равна 60°, значит, . Каждый из указанных углов опирается на дугу AFB, следовательно, градусная мера каждого из них равна

Теорема 2 (об угле между хордой и касательной).

Градусная мера угла, сторонами которого служат касательная и хорда, равна половине градусной меры дуги, расположенной внутри этого угла.

Доказательство.

Первый случай. Пусть угол FAB — острый (рис. 27, о.).

1) Проведем диаметр АС. Тогда вписанный угол СВ А опирается на полуокружность, значит, по следствию 2 он прямой, т. е.

2) Треугольник СВА — прямоугольный, следовательно,

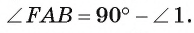
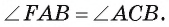
3) Так как диаметр АС перпендикулярен касательной FA, то Таким образом, Так как вписанный угол АСВ опирается на дугу

Следовательно,

Второй случай. Пусть угол FAB — тупой (рис. 27, б). Проведем диаметр СА. Тогда

но дуга ВСА лежит внутри тупого угла FAB.

Свойство пересекающихся хорд. Теорема о касательной и секущей

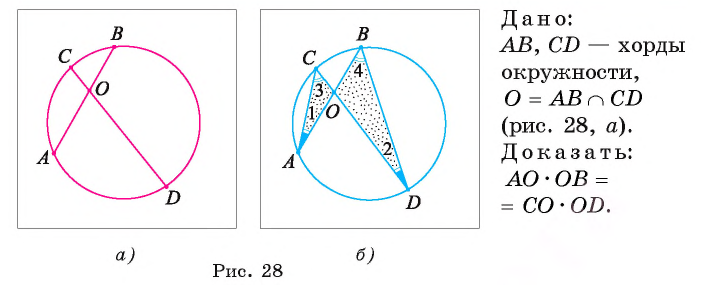
Теорема 3 (об отрезках пересекающихся хорд). Если две хорды окружности пересекаются, то произведение длин отрезков одной хорды равно произведению длин отрезков другой хорды.

1) Проведем хорды АС и BD (рис. 28, б). Рассмотрим треугольники АОСи DOB.

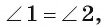
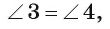
2) Заметим, что так как они вписанные и опираются на одну и ту же дугу СВ. Кроме того, , так как они вписанные и опираются на одну и ту же дугу AD.

3) Треугольник АОС подобен треугольнику DOB по первому признаку подобия треугольников, так как 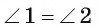и

4) Из подобия треугольников АОС и DOB следует, что

Значит,

Пусть через точку S, лежащую вне окружности, проведена секущая, которая пересекает окружность в точках С и Б, и SC

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

🌟 Видео

111. Окружность, вписанная в правильный многоугольникСкачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Многоугольники. Математика 8 класс | TutorOnlineСкачать

Многоугольники и окружности. ЕГЭ по математике. Be Student SchoolСкачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Задача 6 №27922 ЕГЭ по математике. Урок 139Скачать

Окружность, вписанная в правильный многоугольник | Геометрия 7-9 класс #106 | ИнфоурокСкачать

Окружность, описанная около правильного многоугольника | Геометрия 7-9 класс #105 | ИнфоурокСкачать