Чем отличаются свойства от признаков параллельных прямых (7 видео)

Параллельность прямых

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Содержание

Определение параллельности прямых
Свойства и признаки параллельных прямых
Задача 1
Задача 2
Признаки и свойства параллельных прямых
Признаки параллельных прямых
Свойства параллельных прямых
Признаки и свойства параллельных прямых
Презентация к уроку
💡 Видео

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

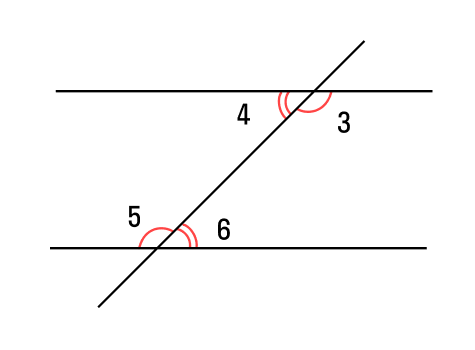
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

два внутренних накрест лежащих угла равны между собой:

два соответственных угла равны между собой:

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Соответственно, ∠MKD = 180° — ∠KDN = 180° — 150° = 30°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

Видео:Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Признаки и свойства параллельных прямых

Видео:Свойства параллельных прямых - 7 класс геометрияСкачать

Признаки параллельных прямых

1. Если две прямые параллельны третьей прямой, то они являются параллельными:

2. Если две прямые перпендикулярны третьей прямой, то они параллельны:

Остальные признаки параллельности прямых основаны на углах, образующихся при пересечении двух прямых третьей.

3. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны:

Если ∠1 + ∠2 = 180°, то a || b.

4. Если соответственные углы равны, то прямые параллельны:

5. Если внутренние накрест лежащие углы равны, то прямые параллельны:

Видео:Параллельность прямых. 10 класс.Скачать

Свойства параллельных прямых

Утверждения, обратные признакам параллельности прямых, являются их свойствами. Они основаны на свойствах углов, образованных пересечением двух параллельных прямых третьей прямой.

1. При пересечении двух параллельных прямых третьей прямой, сумма образованных ими внутренних односторонних углов равна 180°:

Если a || b, то ∠1 + ∠2 = 180°.

2. При пересечении двух параллельных прямых третьей прямой, образованные ими соответственные углы равны:

3. При пересечении двух параллельных прямых третьей прямой, образованные ими накрест лежащие углы равны:

Следующее свойство является частным случаем для каждого предыдущего:

4. Если прямая на плоскости перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой:

Пятое свойство — это аксиома параллельности прямых:

5. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой:

Видео:Геометрия. 7 класс. Параллельные прямые, их признаки и свойства /12.01.2021/Скачать

Признаки и свойства параллельных прямых

Презентация к уроку

По учебнику Л.С.Атанасян и др., Геометрия 7 класс.

Оборудование: Компьютер, проектор, интерактивная доска(по возможности), сигнальные карточки.

Цель урока:

установить взаимосвязь между признаками и свойствами предметов;
рассмотреть свойства параллельных прямых, опираясь на их признаки;
показать учащимся применение свойств параллельных прямых.

Ход урока

1. Актуализация знаний.

Игра “Я знаю все!”

На доске выведена таблица, вызвавшиеся учащиеся по очереди открывают ячейки и отвечают. Остальной класс работает с помощью сигналов “согласны” — зеленый, “нет” — красный.

— Параллельными называются прямые.

— Два отрезка называются параллельными, если.

— Если прямая пересекает одну из параллельных прямых, то она .

— Если две прямые параллельны третьей, то.

— Через любую точку, не лежащую на данной прямой можно провести.

— Если две прямые перпендикулярны третьей, то .

— Прямаях называется секущей по отношению к a и b, если .

— При пересечении aиb секущей m,

углы 1и 5, 2 и 6 называются .

углы 3 и 6, 4 и 5 называются .

углы 6 и 4, 5и 3 называются .

углы 2 и 8, 1 и 7 называются .

углы 1 и 8, 2 и 7 называются .

Если при пересечении двух прямых секущей накрест.

Если при пересечении двух прямых секущей соответственные.

Если при пересечении двух прямых секущей сумма.

Работа ребят оценивается одноклассниками.

2. Изучение нового материала.

Попробуйте отгадать что спрятано у меня на картинке? А вот подсказка:

В садочке есть плод,
Он сладок как мед,
Румян как калач,
Но не круглый, как мяч.
Он под самой ножкой
Вытянут немножко! (груша)

Что помогло вам отгадать картинку? (это — признаки предмета).

Замечательно! А теперь внимание на экран.

Что это? Ну, конечно, дыня. Давайте ее опишем. Дыня – она.

Что мы с вами перечислили? (свойства предмета).

Мы можем узнать, с каким предметом имеем дело, если перечислим его .	— . признаки.
А если мы видим предмет и хотим его описать, то говорим о .	— . свойствах.

Чудесно, а теперь вернемся к геометрии. Мы знаем признаки параллельных прямых.

Вот они – на экране, а как же будут выглядеть СВОЙСТВА? Попробуйте их сформулировать.(Идет работа с доской по формулированию свойствп.п. Щелчок по стрелкам меняет условие и заключение местами).

Хорошо, а теперь внимание на экран, послушаем доказательство одного из свойств.

Будьте предельно внимательны, после этого фрагмента я задам вам вопросы.

Видеофрагмент.

С чего началось доказательство? (с предположения, что накрест лежащие углы не равны.)
Что следовало из этого предположения? (значит можно провести прямую, для которой накрест лежащие углы будут равны.)
Что можно сказать о новой прямой? (она параллельна прямой а, признак параллельности прямых.)
Что получили? (две прямые, параллельные данной прямой, проходят через одну точку)

То есть получили противоречие с аксиомой параллельных прямых.

Значит предположение неверно и накрест лежащие углы равны.

3. Упражнения на понимание:

№1. (Фронтальная работа с классом)

Дано: а//в, какие из утверждений верные?

№2. Дано АС//КМ, какие из утверждений верны?(Учащиеся пишут номера верных равенств в тетрадях, затем меняются ими. Взаимопроверка.)