Задание 6. Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника.

Расширенная теорема синусов гласит, что

где a, b, c – соответствующие стороны треугольника; R – радиус описанной вокруг него окружности. Следовательно, радиус описанной окружности, равен:

Найдем косинус угла C по теореме косинусов:
Соответственно, синус угла C будет равен:
и радиус описанной окружности:

Видео:2080 Боковые стороны равнобедренного треугольника равны 569 основание равно 462Скачать

Боковые стороны треугольника основание равно найдите радиус описанной окружности
Боковые стороны равнобедренного треугольника равны 84,5, основание равно 156. Найдите радиус описанной окружности этого треугольника.
Это задание ещё не решено, приводим решение прототипа.
Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника.
Чтобы найти площадь треугольника ABC, воспользуемся формулой Герона:
Далее по формуле находим:
Приведем еще одно решение.
Проведем высоту CH прямоугольного треугольника ACH и найдем ее:
Следовательно,
Применим теорему синусов к треугольнику ABC, получим откуда
Приведем решение Павла Юкляева.
Треугольник ABC является остроугольным, поскольку 48 2 2 + 40 2 . В равнобедренном остроугольном треугольнике центр описанной окружности О лежит на высоте, проведенной к основанию.
Проведем высоту CH, найдем ее из прямоугольного треугольника ACH:
Из прямоугольного треугольника AOH получим:
а тогда
Приведем решение Артема Абросимова.
Запишем теорему косинусов:
Далее подставим числа:
Зная, найдем
Отрезки AO и OC равны искомому радиусу описанной окружности R, поэтому по теореме косинусов для треугольника AOC получаем:
откуда, подставляя числа, заключаем:
Таким образом, следовательно,
Еще одно решение приведено в задаче 53843.
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Решение №1979 Боковые стороны равнобедренного треугольника равны 104, основание равно 192.
Боковые стороны равнобедренного треугольника равны 104, основание равно 192. Найдите радиус описанной окружности этого треугольника.
Радиус описанной окружности находится по формуле:
Найдём полупериметр:
Площадь треугольника найдём по формуле Герона:
Найдём радиус:
Ответ: 135,2.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
🎥 Видео
Задача 6 №27923 ЕГЭ по математике. Урок 140Скачать

2074 Боковые стороны равнобедренного треугольника равны 5 основание равно 6 найдите радиусСкачать

Геометрия Боковые стороны равнобедренного треугольника равны 4, радиус описанной окружности равенСкачать

Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть II)Скачать

№689. В равнобедренном треугольнике основание равно 10 см, а боковая сторона равна 13 смСкачать

Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

Радиус описанной окружностиСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Задача 6 №27921 ЕГЭ по математике. Урок 138Скачать

Геометрия Найдите радиус окружности описанной около равнобедренного треугольника с основанием 16 смСкачать

ОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать
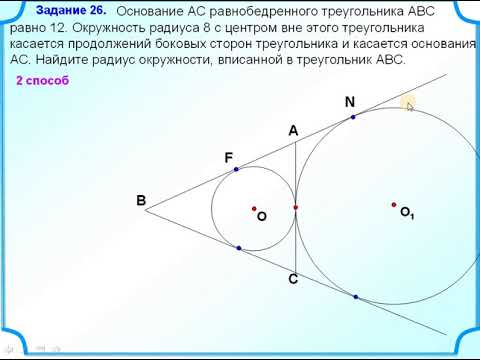
Геометрия, номера 45.1, 46.1 (радиус вписанной окружности)Скачать

№487. Боковая сторона равнобедренного треугольника равна 17 см, а основание равно 16 смСкачать

найти радиус окружности, описанной вокруг треугольникаСкачать

Задание В6 по математике.Скачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать