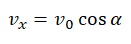Баллистическое движение по окружности

Путь движения тела (например, бомбы, ракеты, летательного аппарата), в котором отсутствует тяга либо управляющая сила и момент, называется баллистической траекторией. Если механизм, приводящий в действие объект, остается рабочим на протяжении всего времени передвижения – он относится к ряду авиационных либо динамических. Траекторию самолета во время полета с выключенными двигателями на большой высоте также можно назвать баллистической.

На объект, который передвигается по заданным координатам, действует лишь механизм, приводящий тело в действие, силы сопротивления и тяжести. Набор таких факторов исключает появление возможности к прямолинейному движению. Данное правило работает даже в космосе.

Тело описывает траекторию, которая подобна эллипсу, гиперболе, параболе либо окружности. Последние два варианта достигаются при второй и первой космических скоростях. Расчеты для движения по параболе или окружности проводятся для определения траектории баллистической ракеты.

Учитывая все параметры при запуске и полете (массу, скорость, температуру и т. д.), выделяют следующие особенности траектории:

• Для того чтобы запустить ракету как можно дальше необходимо подобрать правильный угол. Наилучшим является острый, около 45 º .
• Объект имеет одинаковую начальную и конечную скорости.
• Тело приземляется под таким же углом, как и запускается.
• Время движения объекта от старта и до середины, а также от середины до финишной точки является одинаковым.

Видео:Физика - движение по окружностиСкачать

Свойства траектории и практические значения

Движение тела после прекращения влияния на него движущей силы изучает внешняя баллистика. Данная наука предоставляет расчеты, таблицы, шкалы, прицелы и вырабатывает оптимальные варианты для стрельбы. Баллистическая траектория пули – это кривая линия, которую описывает центр тяжести объекта, находящегося в полете.

Так как на тело влияют сила тяжести и сопротивления, путь, который описывает пуля (снаряд), образует форму кривой линии. Под действием приведенных сил скорость и высота объекта постепенно снижается. Различают несколько траекторий: настильную, навесную и сопряженную.

Первая достигается при использовании угла возвышения, который является меньшим, нежели угол наибольшей дальности. Если при разных траекториях дальность полета остается одинаковой – такую траекторию можно назвать сопряженной. В случае, когда угол возвышения больше, чем угол наибольшей дальности, путь приобретает название навесного.

Траектория баллистического движения объекта (пули, снаряда) состоит из точек и участков:

• Вылета (например, дульный срез ствола) – данная точка является началом пути, и, соответственно, отсчета.
• Горизонта оружия – этот участок проходит через точку вылета. Траектория пересекает ее дважды: при выпуске и падении.
• Участка возвышения – это линия, которая является продолжением горизонта образует вертикальную плоскость. Данный участок носит название плоскости стрельбы.
• Вершины траектории – это точка, которая находится посредине между начальной и конечной точками (выстрела и падения), имеет наивысший угол на протяжении всего пути.
• Наводки – мишень или место прицела и начало движения объекта образуют линию прицеливания. Между горизонтом оружия и конечной целью формируется угол прицеливания.

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Ракеты: особенности запуска и движения

Различают управляемые и неуправляемые баллистические ракеты. На формирование траектории также влияют внешние и наружные факторы (силы сопротивления, трения, вес, температура, требуемая дальность полета и т.д).

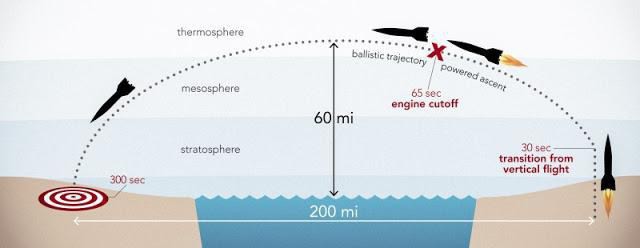
Общий путь запущенного тела можно описать следующими этапами:

• Запуск. При этом ракета переходит в первую стадию и начинает свое движение. С этого момента и начинается измерение высоты траектории полета баллистической ракеты.
• Приблизительно через минуту запускается второй двигатель.
• Через 60 секунд после второго этапа запускается третий двигатель.
• Далее тело входит в атмосферу.
• В последнюю очередь происходит взрыв боевых головок.

Видео:Урок 89. Движение по окружности (ч.1)Скачать

Запуск ракеты и формирование кривой передвижения

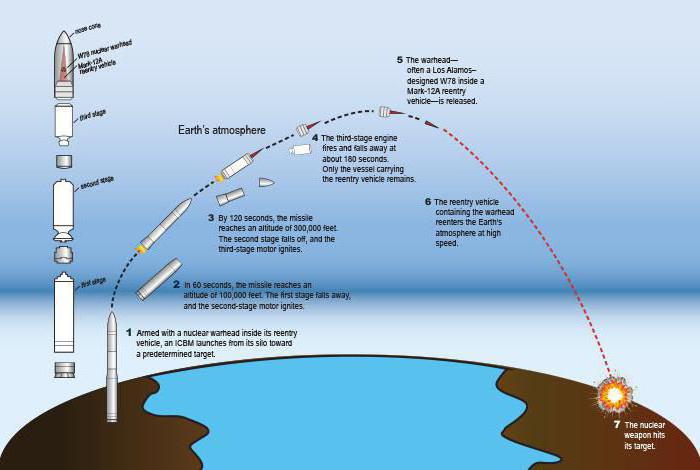
Кривая передвижения ракеты состоит из трех частей: периода запуска, свободного полета и повторного входа в земную атмосферу.

Боевые снаряды запускаются с фиксированной точки переносных установок, а также транспортных средств (судов, субмарин). Приведение в полет продолжается от десятых тысячных секунд до нескольких минут. Свободное падение составляет наибольшую часть траектории полета баллистической ракеты.

Преимуществами запуска такого приспособления являются:

• Продолжительное время свободного полета. Благодаря этому свойству существенно уменьшается расход топлива в сравнении с другими ракетами. Для полета прототипов (крылатых ракет) используются более экономичные двигатели (например, реактивные).
• На скорости, с которой движется межконтинентальная орудие (примерно 5 тыс. м/с), перехват дается с большой сложностью.
• Баллистическая ракета в состоянии поразить цель на расстоянии до 10 тыс. км.

В теории путь передвижения снаряда – это явление из общей теории физики, раздела динамики твердых тел в движении. Относительно данных объектов рассматривается передвижение центра масс и движение вокруг него. Первое относится к характеристике объекта, совершающего полет, второе – к устойчивости и управлению.

Так как тело имеет программные траектории для совершения полета, расчет баллистической траектории ракеты определяется физическими и динамическими расчетами.

Видео:Движение тела, брошенного под углом к горизонтуСкачать

Современные разработки в баллистике

Поскольку боевые ракеты любого вида являются опасными для жизнедеятельности, главной задачей обороны является усовершенствование точек для запуска поражающих систем. Последние должны обеспечить полную нейтрализацию межконтинентального и баллистического оружия в любой точке движения. К рассмотрению предложена многоярусная система:

• Данное изобретение состоит из отдельных ярусов, каждый из которых имеет свое назначение: первые два будут оснащены оружием лазерного типа (самонаводящиеся ракеты, электромагнитные пушки).
• Следующих два участка оснащаются тем же оружием, но предназначенного для поражения головных частей оружия противника.

Разработки в оборонном ракетостроении не стоят на месте. Ученные занимаются модернизацией квазибаллистической ракеты. Последняя представлена как объект, имеющий низкий путь в атмосфере, но при этом резко изменяющий направление и диапазон.

Баллистическая траектория такой ракеты не влияет на скорость: даже на предельно низкой высоте объект передвигается быстрее, нежели обычный. Например, разработка РФ «Искандер» летит на сверхзвуковой скорости – от 2100 до 2600 м/с при массе 4 кг 615 г, круизы ракеты передвигают боеголовку весом до 800 кг. При полете маневрирует и уклоняется от противоракетной обороны.

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Межконтинентальное оружие: теория управления и составляющие

Многоступенчатые баллистические ракеты носят название межконтинентальных. Такое название появилось неспроста: из-за большой дальности полета становится возможным перебросить груз на другой конец Земли. Основным боевым веществом (зарядом), в основном, является атомное либо термоядерное вещество. Последнее размещается в передней части снаряда.

Далее в конструкции устанавливается система управления, двигатели и баки с топливом. Габариты и масса зависят от требуемой дальности полета: чем больше расстояние, тем выше стартовый вес и габариты конструкции.

Баллистическую траекторию полета МБР отличают от траектории иных ракет по высоте. Многоступенчатая ракета проходит процесс запуска, затем на протяжении нескольких секунд движется вверх под прямым углом. Системой управления обеспечивается направления орудия в сторону цели. Первая ступень привода ракеты после полного выгорания самостоятельно отделяется, в этот же момент запускается следующая. При достижении заданной скорости и высоты полета ракета начинает стремительно двигаться вниз к цели. Скорость полета к объекту назначения достигает 25 тыс. км/ч.

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Мировые разработки ракет специального назначения

Около 20 лет назад в ходе модернизации одного из ракетных комплексов средней дальности был принят проект противокорабельных баллистических ракет. Такая конструкция размещается на автономной пусковой платформе. Вес снаряда составляет 15 тонн, а дальность пуска – почти 1,5 км.

Траектория баллистической ракеты для уничтожения кораблей не поддается для быстрых расчетов, поэтому предугадать действия противника и устранить данное орудие невозможно.

Такая разработка имеет преимущества:

• Дальность пуска. Эта величина в 2-3 раза больше, нежели у прототипов.
• Скорость и высота полета делают боевое оружие неуязвимым для противоракетной обороны.

Мировые специалисты уверены в том, что оружие массового поражения все-таки можно обнаружить и нейтрализовать. Для таких целей используются специальные разведывательные заорбитные станции, авиацию, подводные лодки, корабли и др. Самым главным «противодействием» является космическая разведка, которая представлена в виде радиолокационных станций.

Баллистическая траектория определяется системой разведки. Полученные данные передаются по месту назначения. Основной проблемой является быстрое устаревание информации – за короткий период времени данные теряют свою актуальность и могут расходиться с настоящим местом нахождения оружия на расстояние до 50 км.

Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

Характеристики боевых комплексов отечественной оборонной промышленности

Наиболее мощным оружием нынешнего времени считается межконтинентальная баллистическая ракета, которая размещается стационарно. Отечественный ракетный комплекс «Р-36М2» является одним из наилучших. На нем размещается сверхпрочное боевое орудие «15А18М», которое способно нести до 36 ядерных снарядов индивидуального точного наведения.

Баллистическую траекторию полета такого оружия практически невозможно предугадать, соответственно, нейтрализация ракеты также предоставляет сложности. Боевая мощность снаряда составляет 20 Мт. Если данный боеприпас взорвется на низкой высоте – системы связи, управления, противоракетной обороны выйдут из строя.

Модификации приведенной ракетной установки можно использовать и в мирных целях.

Среди твердотопливных ракет особенно мощной считается «РТ-23 УТТХ». Такое приспособление базируется автономно (мобильно). В стационарной станции-прототипе («15Ж60») стартовая тяга выше на 0,3, в сравнении с мобильной версией.

Запуск ракет, который проводится непосредственно со станций сложно нейтрализовать, ведь количество снарядов может достигать 92 единиц.

Видео:Баллистическое движениеСкачать

Ракетные комплексы и установки заграничной оборонной промышленности

Высота баллистической траектории ракеты американского комплекса «Минитмен-3» не особо отличается от характеристик полета отечественных изобретений.

Комплекс, который разработан в США, является единственным «защитником» Северной Америки среди оружия такого вида до сегодняшнего дня. Несмотря на давность изобретения, показатели устойчивости орудия являются неплохими и в нынешнее время, ведь ракеты комплекса могли противостоять противоракетной обороне, а также поразить цель с высоким уровнем защиты. Активный участок полета непродолжительный, и составляет 160 с.

Другое изобретение американцев – «Пискипер». Он также мог обеспечить точное попадание в цель благодаря наивыгоднейшей траектории баллистического движения. Специалисты утверждают, что боевые возможности приведенного комплекса почти в 8 раз выше, нежели у «Минитмена». Боевое дежурство «Пискипера» составляло 30 секунд.

Видео:Физика | Равномерное движение по окружностиСкачать

Полет снаряда и движение в атмосфере

Из раздела динамики известно влияние плотности воздуха на скорость передвижения любого тела в различных слоях атмосферы. Функция последнего параметра учитывает зависимость плотности непосредственно от высоты полета и выражается в зависимости:

где у – высота полета снаряда (м).

Расчет параметров, а также траектории межконтинентальной баллистической ракеты можно производить с помощью специальных программ на ЭВМ. Последние приведут ведомости, а также данные о высоте полета, скорости и ускорении, продолжительности каждого этапа.

Экспериментальная часть подтверждает расчетные характеристики, и доказывает, что на скорость оказывает влияние форма снаряда (чем лучше обтекаемость, тем выше скорость).

Видео:Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

Управляемое оружие массового поражения прошлого века

Все оружие приведенного типа можно разделить на две группы: наземное и авиационное. Наземным называется такие приспособления, запуск которых осуществляется со стационарных станций (например, шахт). Авиационное, соответственно, запускается с корабля-носителя (самолета).

К группе наземных относятся баллистические, крылатые и зенитные ракеты. К авиационным – самолеты-снаряды, АБР и управляемые снаряды воздушного боя.

Основной характеристикой расчета баллистической траектории движения является высота (несколько тысяч километров над слоем атмосферы). При заданном уровне над уровнем Земли снаряды достигают высоких скоростей и создают огромные сложности для их выявления и нейтрализации ПРО.

Известными БР, которые рассчитаны на среднюю дальность полета, являются: «Титан», «Тор», «Юпитер», «Атлас» и др.

Баллистическая траектория ракеты, которая запускается из точки и попадает по заданным координатам, имеет форму эллипса. Размер и протяженность дуги зависит от начальных параметров: скорости, угла запуска, массы. Если скорость снаряда приравнивается к первой космической (8 км/с), боевое орудие, которое запущено параллельно к горизонту, превратится в спутник планеты с круговой орбитой.

Несмотря на постоянное усовершенствование в области обороны, путь полета боевого снаряда практически не изменяется. На текущий момент технологии не в состоянии нарушить законы физики, которым подчиняются все тела. Небольшим исключением являются ракеты с самонаведением – они могут менять направление в зависимости от перемещения цели.

Изобретатели противоракетных комплексов также модернизируют и разрабатывают орудие для уничтожения средств массового поражения нового поколения.

Видео:Баллистическое движение | Физика ЕГЭ | УмскулСкачать

Баллистическое движение — характеристика, основные формулы и уравнения

Как упадет брошенный предмет, по какой траектории полетит пуля и как рассчитать правильное направление для попадания в цель – всё это объясняется таким понятием как баллистическое движение и изучается соответствующей наукой.

Наверное каждый при просмотре фильмов о работе экспертов-криминалистов слышал выражение «аэробаллистическая экспертиза», и удивлялся тому, как лихо они определяют местоположение стрелка, и тип, а иногда и модель оружия, из которого был произведен, зачастую, фатальный выстрел.

Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Понятие баллистики

Определение баллистики звучит следующим образом – наука о движении тел, двигающихся в пространстве. Она изучает в первую очередь принципы движения всевозможных объектов, в частности пуль и снарядов, а также законы природы, влияющие на это движение и способность тела преодолевать возникшие на его пути преграды.

Физика и математика — вот основы, на которых базируется эта наука, они позволяют при должных знаниях рассчитывать траекторию полёта пули, исходя из воздействия на неё внешних сил, и её проникающую способность.

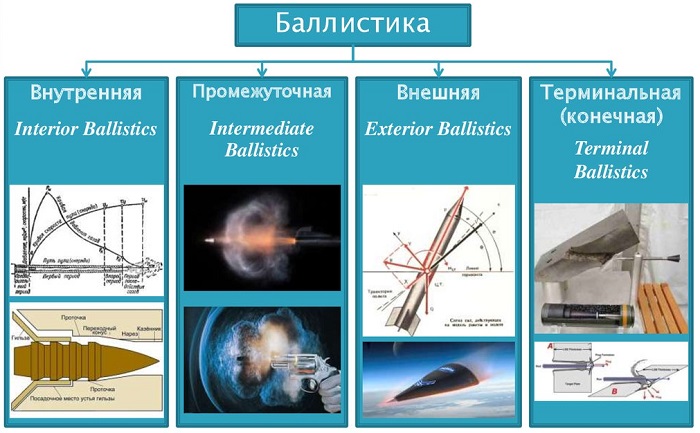
Сама же наука о законах полета снарядов делится на 4 направления:

Исследование движения пули или снаряда в канале ствола орудия изучает направление, которое называется внутренняя баллистика.

Поведение снаряда на выходе из канала ствола и в районе дульного среза исследуется промежуточной баллистикой и используется в разработке пламегасящих устройств и глушителей.

Вопросы движения снаряда в атмосфере и при воздействии внешних факторов изучаются внешней баллистикой. Основная область её применения – установление поправок на упреждение и влияние скорости ветра на траекторию.

Изучение проникающей способности снаряда – цель исследований баллистики под названием преградная (терминальная), которую изучают специалисты по вопросам бронезащиты.

Видео:Центростремительное ускорение. 9 класс.Скачать

История возникновения баллистики

Испокон веков основным занятием человека являлось уничтожение себе подобных. Сперва для этого использовались булыжники и палки, после чего человечество пришло к тому, что дистанционное оружие дает целый ряд преимуществ его владельцу.

Так или иначе баллистика изучалась по мере развития человечества, параллельно с развитием механизмов для поражения противника на расстоянии.

Метательные камни, ножи и дротики, ручные пращи, луки, арбалеты, а впоследствии – баллисты, катапульты, требушеты, толлеоны и, в конце концов, огнестрельное оружие и артиллерийские орудия — все эти средства толкали науку баллистики на протяжении всей своей истории.

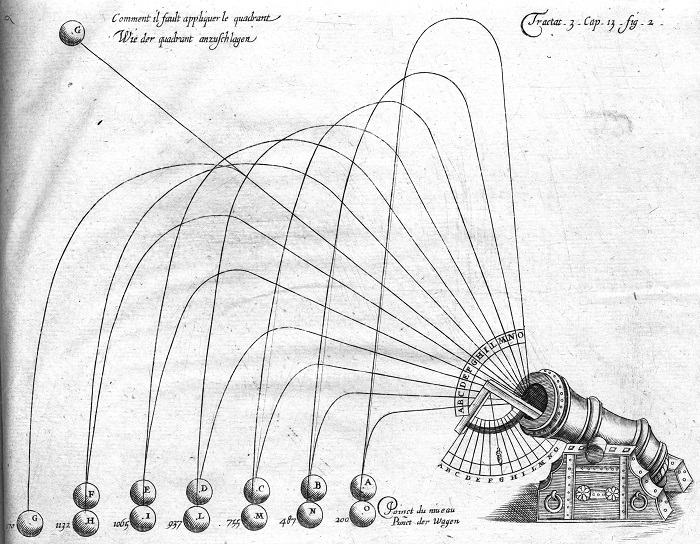
Начало изучения траектории полета снаряда, как науки, было положено Николло Тарталья в 1537 году, начавшим исследование кривой движения этого тела. Продолжил изучение Галилей, сформулировав параболическую теорию.

Развивал данную тему и Ньютон, благодаря изучению законов воздушного сопротивления которого стало возможным доказать невозможность параболической кривой полета снаряда. Его дело продолжил Бенджамин Робинс, основное исследование которого — расчет начальной скорости ядра.

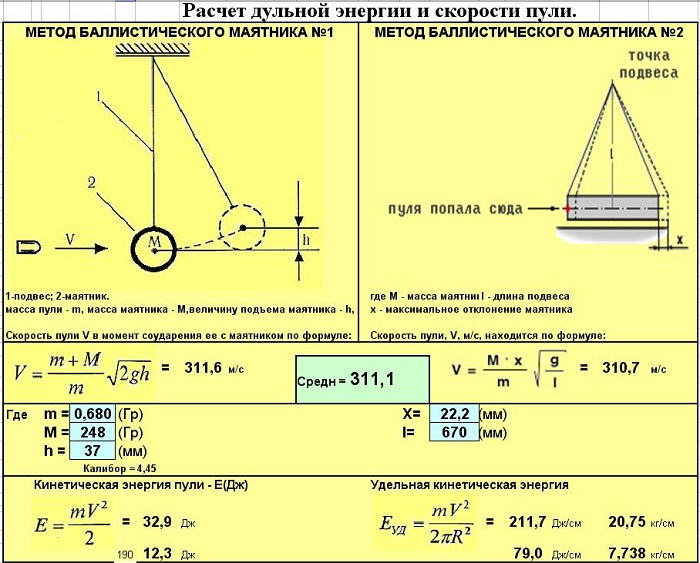
Он даже изобрел актуальный по сей день баллистический маятник. Прибор, с помощью которого определяют эффективность взрывчатых веществ, фиксируя при их подрыве угол отклонения маятника.

Далее баллистика развивалась семимильными шагами. Вошедшее в обиход в начале XIX века нарезное оружие, а также использование адаптированных под него снарядов и нового образца патрона, с пулей продолговатой формы, а точнее – необходимость изучения их эффективности и дальнейшей оптимизации, стали серьезным толчком в изучении данной науки, поскольку характеристики нового оружия были весьма высоки, что обуславливало широкую его популярность, и как следствие – высокий спрос.

Одним из ключевых витков истории баллистики стала разработка численного метода интегрирования дифференциальных уравнений, созданного Карлом Рунге и Мартином Кутта. Определенные элементы их метода позволяли с максимальной точностью вести расчеты траектории тел в пространстве.

Появлялись всё новые виды вооружения, конструкторы отчаянно экспериментировали с длиной ствола, внутренними нарезами и наполнением патрона, двигая науку вперед.

Видео:Свободное падение. Баллистика. Движение по окружности. Решение задач ЕГЭСкачать

Баллистическая траектория

Итак, что же в итоге представляет собой баллистическая траектория? Современная энциклопедия гласит: «Это траектория движения свободно брошенного тела под действием только силы тяжести».

Например, межконтинентальные баллистические ракеты считаются таковыми, поскольку продолжают своё движение к цели после выключения двигателей, как раз-таки по траектории, которую называют баллистической.

Здесь же – расчет ведения огня по настильной траектории, проще говоря – плавно опускающейся линии по ходу полета снаряда, и расчет возможности преодолевать возвышения по пути к конечной точке.

Фактически, таковым является движение любого тела в пространстве, при отсутствии какой-либо дополнительной тяги.

Видео:Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Основные формулы баллистического движения

При расчетах и изучении баллистического движения любого тела, стоит обратить внимание на огромное количество факторов – массу, скорость и обтекаемость тела, атмосферные условия и многое-многое другое. Но даже при учете этого, в баллистике есть свои основные формулы, применяемые в исследованиях.

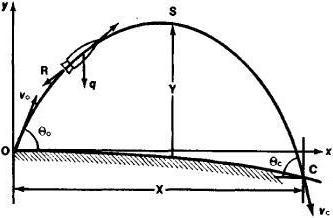
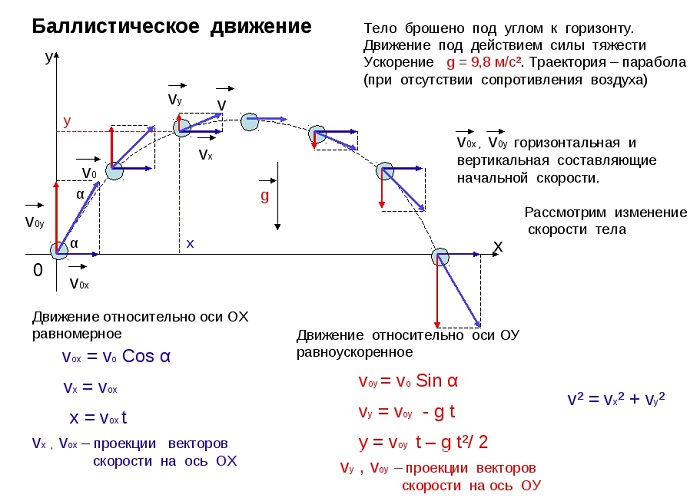
На брошенное под углом к горизонту тело в полете действует по меньшей мере – сила тяжести и сопротивление воздуха. Если исключить из этого силу сопротивления, то, согласно 2-го закону Ньютона, тело движется с ускорением, равным ускорению свободного падения; проекции ускорения на координатные оси равны ах = 0, ау = -g.

Проекции скорости тела, следовательно, изменяются со временем следующим образом:

где V₀ — начальная скорость, α – угол бросания.

Координаты тела, следовательно, изменяются так:

y = y₀ + V₀ * t * sin α – 0,5 * g * t 2 .

Если за точку отсчета берутся координаты х = у = 0, то:

x = V₀ * t * cos α;

y = V₀ * t * sin α – 0,5 * g * t 2 .

Дальнейшие расчеты производятся при введении таких переменных как дальность полета и время, в итоге же получается финальное уравнение траектории движения. Выглядит оно следующим образом:

y = x * tg α – g * x 2 / 2 * V₀ 2 * cos 2 α.

Видео:Урок 90. Движение по окружности (ч.2)Скачать

Движение тела, брошенного под углом к горизонту

теория по физике 🧲 кинематика

Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.

Важные факты! График движения тела, брошенного под углом к горизонту:

α — угол, под которым было брошено тело

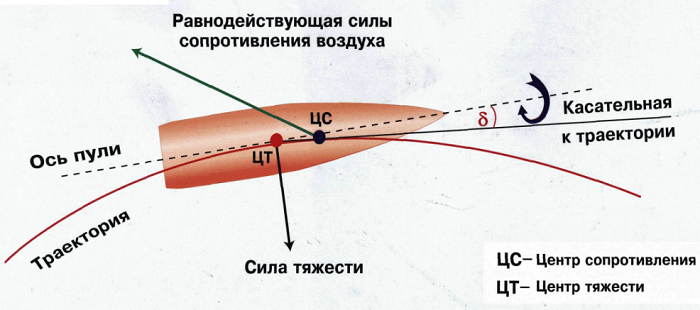
1. Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
2. Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v_0x = v₀cosα. Ее проекция на ось ОУ равна v_0y = v₀sinα.
3. Проекция мгновенной скорости на ось ОХ равна: v_x = v₀ cosα. Ее проекция на ось ОУ равна нулю: v_y = v₀ sinα – gt.
4. Проекция ускорения свободного падения на ось ОХ равна нулю: g_x = 0. Ее проекция на ось ОУ равна –g: g_y = –g.

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Кинематические характеристики

Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:

Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:

Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:

Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: v_y = 0. Время подъема определяется следующей формулой:

Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:

Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:

Подставляя в выражение формулу полного времени полета, получаем:

Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:

Учитывая, что x₀ = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v₀ cosα, данная формула принимает вид:

Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:

Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v₀ sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:

Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:

Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?

Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:

Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:

Видео:Кинематика. Движение по окружности. Урок 4Скачать

Тело, брошенное под углом к горизонту с некоторой высоты

Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.

График движения тела, брошенного под углом к горизонту с некоторой высоты:

Время падения тела больше времени его подъема: t_пад > t_под.

Полное время полета равно:

Уравнение координаты x:

Уравнение координаты y:

Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.

Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:

x = v₀ cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.

Алгоритм решения

Решение

Запишем исходные данные:

Построим чертеж и укажем на нем все необходимое:

Нулевой уровень — точка D.

Закон сохранения энергии:

Потенциальная энергия шарика в точке А равна:

Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.

В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:

Перед ударом кинетическая энергия шарика равна:

Согласно закону сохранения энергии:

E p A = E p B + E k B

m g H = m g l 1 + m v 2 2 . .

Отсюда высота H равна:

H = m g l 1 m g . . + m v 2 2 m g . . = l 1 + v 2 2 g . .

Относительно точки В шарик поднимется на высоту h – l₁. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:

h − l 1 = v 2 sin 2 . β 2 g . . = v 2 sin 2 . ( 90 − 2 α ) o 2 g . .

l 1 = h − v 2 sin 2 . ( 90 − 2 α ) o 2 g . .

Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:

H = l 1 + v 2 2 g . . = h − ( g t ) 2 sin 2 . ( 90 − 2 α ) o 2 g . . + ( g t ) 2 2 g . .

H = h − g t 2 sin 2 . ( 90 − 2 α ) 2 . . + g t 2 2 . . = h − g t 2 2 . . ( sin 2 . ( 90 − 2 α ) o − 1 )

H = 1 , 4 − 10 · 0 , 4 2 2 . . ( sin 2 . ( 90 − 6 0 ) o − 1 )

H = 1 , 4 − 5 · 0 , 16 ( sin 2 . 3 0 o − 1 )

H = 1 , 4 − 0 , 8 ( ( 1 2 . . ) 2 − 1 ) = 1 , 4 − 0 , 8 ( 1 4 . . − 1 )

H = 1 , 4 + 0 , 6 = 2 ( м )

pазбирался: Алиса Никитина | обсудить разбор | оценить

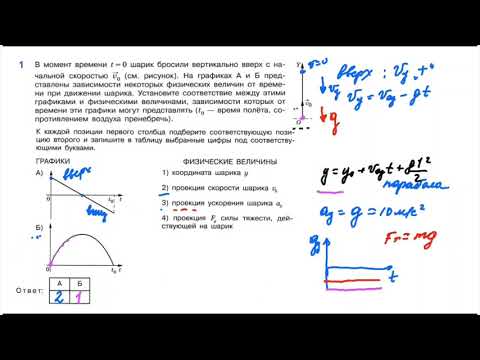
В момент t=0 мячик бросают с начальной скоростью v₀ под углом α к горизонту с балкона высотой h (см. рисунок).

Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).

К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.

Алгоритм решения

1. Установить вид механического движения, исходя из условий задачи.
2. Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
3. Определить, как зависят эти величины от времени.
4. Установить соответствие между графиками и величинами.

Решение

Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.

Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.

Координата x меняется согласно уравнению координаты x:

Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:

Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:

В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.

Формула проекции скорости мячика на ось ОХ:

Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.

Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.

Остается последний вариант — координата y. Уравнение этой координаты имеет вид:

Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.

Теперь записываем установленные соответствия в порядке АБ: 42.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?

Для каждой величины определите соответствующий характер изменения:

1. увеличивается
2. уменьшается
3. не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

1. Сделать чертеж, иллюстрирующий ситуацию.
2. Записать формулы, определяющие указанные в условии задачи величины.
3. Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.

Решение

Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).

Горизонтальная составляющая скорости шарика определяется формулой:

Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).

Ответом будет следующая последовательность цифр — 33.

pазбирался: Алиса Никитина | обсудить разбор | оценить

🎥 Видео

КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

ДВИЖЕНИЕ ПО ОКРУЖНОСТИ 9 класс физика ПерышкинСкачать