- Первый признак подобия треугольников
- Второй признак подобия треугольников
- Третий признак подобия треугольников
- Задачи
- Ответы к задачам
- Атанасян признаки подобия треугольников
- Урок 36. Решение задач на применение признаков подобия треугольников
- I. Организационный момент.
- II. Актуализация знаний учащихся
- III. Самостоятельная работа
- I уровень сложности
- II уровень сложности
- III уровень сложности
- IV. Рефлексия учебной деятельности
- Урок по теме «Признаки подобия треугольников» методическая разработка по геометрии (8 класс)
- Скачать:
- Предварительный просмотр:
- 📹 Видео
Первый признак подобия треугольников
| Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. |
По теореме о сумме углов треугольника ∠C = 180° — ∠A — ∠B, ∠C1 = 180° — ∠A1 — ∠B1, и, значит, ∠C = ∠C1. Таким образом, углы треугольника АВС соответственно равны углам треугольника А1В1С1.
Докажем, что стороны треугольника АВС пропорциональны сходственным сторонам треугольника А1В1С1. Так как ∠A = ∠A1 и ∠C = ∠C1, то 

Из этих равенств следует, что 

Итак, стороны треугольника АВС пропорциональны сходственным сторонам треугольника А1В1С1.
Второй признак подобия треугольников
| Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны. |
Рассмотрим два треугольника АВС и А1В1С1, у которых 
Рассмотрим треугольник АВС2, у которого ∠1 = ∠A1, ∠2 = ∠B1 (рис. 192, б). Треугольники АВС2 и А1В1С1 подобны по первому признаку подобия треугольников, поэтому 

Треугольники АВС и АВС2 равны по двум сторонам и углу между ними (АВ — общая сторона, АС = АС2 и ∠A = ∠1, поскольку ∠A = ∠A1 и ∠1 = ∠A1). Отсюда следует, что ∠B = ∠2, а так как ∠2 = ∠B1, то ∠B = ∠B1.
Третий признак подобия треугольников
| Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны. |
Пусть стороны треугольников АВС и А1В1С1 пропорциональны:
Докажем, что ΔАВС ∼ ΔА1В1С1. Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что ∠A = ∠A1. Рассмотрим треугольник АВС2, у которого ∠1 = ∠A1, ∠2 = ∠B1 (см. рис. 192,6). Треугольники АВС2 и А1В1С1 подобны по первому признаку подобия треугольников, поэтому
Сравнивая эти равенства с равенствами (1), получаем: ВС = ВС2, СА = С2А. Треугольники АВС и АВС2 равны по трём сторонам. Отсюда следует, что ∠A = ∠1, а так как ∠1 = ∠A1, то ∠A = ∠A1.
Задачи
550. По данным рисунка 193 найдите х и у.
551. На стороне CD параллелограмма ABCD отмечена точка Е. Прямые АЕ и ВС пересекаются в точке F. Найдите: a) EF и FC, если DE = 8 см, ЕС = 4 см, ВС= 7 см, А? = 10см; б) DE и ЕС, если АВ = 8 см, AD- 5 см, CF = 2 см.
552. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите: а) АВ, если ОВ = 4 см, ОЕ=10см, DС = 25 см; б) 
553. Подобны ли равнобедренные треугольники, если они имеют: а) по равному острому углу; б) по равному тупому углу; в) по прямому углу? Ответ обоснуйте.
554. Основания трапеции равны 5 см и 8 см. Боковые стороны, равные 3,6 см и 3,9 см, продолжены до пересечения в точке М. Найдите расстояния от точки М до концов меньшего основания.
555. Точки М, N и Р лежат соответственно на сторонах АВ, ВС и С А треугольника АВС, причём MN || АС, NP || АВ. Найдите стороны четырёхугольника AMNP, если: а) АВ = 10 см, АС = 15 см, PN : MN = 2 : 3; б) АМ = АР, АВ = а, АС = b.
556. Стороны угла О пересечены параллельными прямыми АВ и CD. Докажите, что отрезки О А и АС пропорциональны отрезкам ОВ и BD (рис. 194).
Проведём через точку А прямую АС,, параллельную прямой BD (С, — точка пересечения этой прямой с прямой CD). Тогда ΔОАВ ∼ ΔАСС1 по первому признаку подобия треугольников (∠O = ∠CAC1, ∠OAB = ∠C), следовательно, 

557. Стороны угла А пересечены параллельными прямыми ВС и DE, причём точки В и D лежат на одной стороне угла, а С и Е — на другой. Найдите: а) АС, если СЕ = 10 см, АD = 22 см, BD = 8 см; б) BD и DE, если АВ = 10 см, АС = 8 см, BС = 4 см, СЕ = 4 см; в) ВС, если АВ : BD = 2 : 1 и DE = 12 см.
558. Прямые а и b пересечены параллельными прямыми АА1, ВВ1, СС1, причём точки А, В и С лежат на прямой а, а точки А1, В1 и С1 — на прямой b. Докажите, что
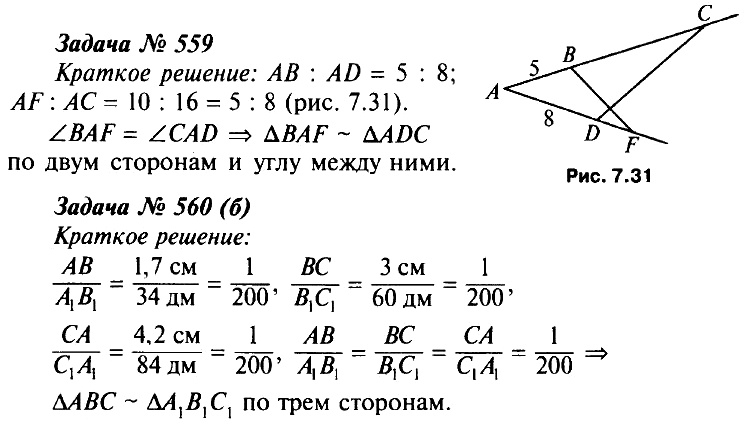
559. На одной из сторон данного угла А отложены отрезки АВ = 5 см и АС= 16 см. На другой стороне этого же угла отложены отрезки АD = 8 см и АF =10см. Подобны ли треугольники АСD и AFB? Ответ обоснуйте.
560. Подобны ли треугольники АВС и А1В1С1, если: а) АВ = 3см, ВС = 5 см, СА = 7 см, А1В1 = 4,5 см, В1С1 = 7,5 см, С1А1 = 10,5 см; б) АВ = 1,7 см, ВС = 3 см, СА = 4,2 см, А1В1 = 34 дм, В1С1 = 60 дм, С1А1 = 84 дм?
561. Докажите, что два равносторонних треугольника подобны.
562. В треугольнике АВС сторона АВ равна а, а высота СН равна h. Найдите сторону квадрата, вписанного в треугольник АВС так, что две соседние вершины квадрата лежат на стороне АВ, а две другие — соответственно на сторонах АС и ВС.
563. Через точку М, взятую на медиане AD треугольника АВС, и вершину В проведена прямая, пересекающая сторону АС в точке К. Найдите отношение 

Ответы к задачам
551. a) EF = 5см, FC = 3,5см; б) DE = 

552. а) 10 см; б) 
553. а) Не всегда; б) да; в) да.
554. 6 см и 6,5 см.
555. а) 5 см, 5 см, 7,5 см, 7,5 см; б) все четыре стороны равны 
557. а) 17,5 см; б) ВD = 5 см, DЕ = 6 см; в) 8см.
558. Указание. Если прямые а и b не параллельны, то через точку А провести прямую, параллельную прямой b.
562. 
563. а) 1/2; б) 1/4; Указание. Через точку D провести прямую, параллельную ВК.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Атанасян признаки подобия треугольников
Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 36. Решение задач на применение признаков подобия треугольников. Вернуться к Списку уроков Тематического планирования.
Видео:Геометрия 8 класс. Первый признак подобия треугольниковСкачать
Урок 36. Решение задач на применение
признаков подобия треугольников
Основные дидактические цели урока: сформировать у учащихся навыки применения признаков подобия треугольников при решении задач; совершенствовать навыки доказательств теорем.
Ход урока
I. Организационный момент.
Мотивация к учебной деятельности. (Учитель сообщает тему урока, формулирует цели урока.)
II. Актуализация знаний учащихся
- Проверка домашнего задания. (Учитель проверяет решение задач № 559, 560 (б). Два ученика заранее готовят решение на доске.)
- Теоретический опрос. (Два ученика готовят доказательства теорем у доски.)
- Сформулируйте признаки подобия треугольников.
- Докажите теоремы, выражающие второй и третий признаки подобия треугольников.
- Работа по индивидуальным карточкам. (3—6 учеников работают по карточкам во время теоретического опроса.)
I уровень сложности
Подобны ли треугольники АВС и А1В1С1, если известно, что:
II уровень сложности
- Прямая, параллельная стороне MN треугольника MNK, пересекает стороны КМ и KN в точках Е и F соответственно, КЕ = 6 см, KN = 10 см, KF = 9 см, KN = 15 см. Найдите отношения. a) EF: MN, б) PKMN : РКЕF, в) SKEF : SKMN.
- Точка Е — середина стороны AD параллелограмма ABCD. В каком отношении прямая BE делит диагональ АС параллелограмма? Найдите отношение площади треугольника АВЕ и четырехугольника BCDE.
III уровень сложности
- Основания трапеции равны 9 и 6 см, а высота равна 10 см. Найдите разность расстояний от точки пересечения диагоналей трапеции до ее оснований.
- Докажите признак подобия прямоугольных треугольников по гипотенузе и катету.
- Решение задач по готовым чертежам.
- 1) Рис. 7.32. Найти: ∠C1, В1С1.
- 2) Рис. 7.33. Найти: ∠C, ∠C1
- 3) Рис. 7.34. Найти: ВМ.
- 4) Рис. 7.35. Найти: ВС.
- 5) Рис. 7.36. Найти: ∠DCA.
- 6) Рис. 7.37. Найти АВ, NC.
Ответы к задачам по готовым чертежам:
- 1) ∠C1 = 71°, В1С1 = 15 см.
- 2) ∠C = ∠C1 = 60°.
- 3) ВМ = 6 см.
- 4) BC = 20/3.
- 5)Обратите внимание! Ответ автора задания ∠DCA = 90°. Однако, этот ответ нельзя признать правильным в виду каких-то опечаток в рис.7.36. Единственный вывод из рисунка: треугольники ABC и АCD подобны (по трем сторонам), но в таком случае ответ должен быть 80°, а не 90°. Но самый противоречивый момент связан с тем, что треугольники с заявленными сторонами и углами не существуют. Если считать, что стороны на рисунке указаны правильно, то вместо 80° должно быть указано 92,73°, а вместо 55° должно быть 45,52°. Тогда правильный ответ будет ∠DCA = 92,73°.
- 6) АВ = 8, NC= 8.
(После окончания самостоятельного решения задач и самопроверки по готовым ответам выполняется самооценка.) Критерии оценивания:
- оценка «5» — правильно решены пять-шесть задачи;
- оценка «4» — правильно решены четыре задачи;
- оценка «3» — правильно решены две-три задачи;
- оценка «2» — не ставится.
(Учащиеся, справившиеся со всеми задачами, решают дополнительные задачи.)
Дополнительные задачи
- Диагональ АС трапеции ABCD (АВ||CD) делит ее на два подобных треугольника. Найдите площадь трапеции ABCD, если АВ = 25 см, ВС = 20 см, АС = 15 см.
Ответ : SABCD = 204 см 2 .
- Угол В треугольника AВС в два раза больше угла А. Биссектриса угла В делит сторону АС на части AD = 6 см и CD = 3 см. Найдите стороны треугольника АВС.
Ответ : АС = 9 см, АВ = 6√3 см, ВС = 3√3 см.
III. Самостоятельная работа
I уровень сложности
Вариант 1
- Рис. 7.38. Доказать: ΔАВС
ΔА1В1С1
Вариант 2
- Рис. 7.39. Доказать: ΔАВС
ΔА1B1С1.
II уровень сложности
Вариант 1.
- Рис. 7.40. Доказать: ΔАВС
ΔА1В1С1
Вариант 2
- Рис. 7.41. Доказать: ΔМВН
ΔСВA.
III уровень сложности
Вариант 1
- Дано: ∠1 = ∠2, AD = 4, АС = 9 (рис. 7.42). Найти: АВ, SABD : SABC.
- Диагонали четырехугольника ABCD пересекаются в точке О, АО • ВО = СО • DO. Докажите, что площади треугольников ACD и ABD равны.
Вариант 2
- Дано: ВС ⊥ АС, МН ⊥ ВС, 2МС = ВС, МН = 0,5АС (рис. 7.43). Доказать: АВ||СН. Найти. SАВС : SMCH.
- В трапеции ABCD AD и ВС — основания, О — точка пересечения диагоналей, АО : ОС = 3 : 2. Найдите отношение площадей треугольников АВС и ACD.
( Ответы на самостоятельную работу смотрите в уроке 37)
IV. Рефлексия учебной деятельности
- Сформулируйте признаки подобия треугольников.
- В каком случае подобны равносторонние, равнобедренные, прямоугольные треугольники?
Домашнее задание. Решить задачи № 562, 563, 604, 605.
Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 36. Решение задач на применение признаков подобия треугольников.
Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Урок по теме «Признаки подобия треугольников»
методическая разработка по геометрии (8 класс)
Разработка урока геометрии в 8 классе по теме «Признаки подобия треугольников» УМК Атанасян.
Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Скачать:
| Вложение | Размер |
|---|---|
| priznaki_podobiya_treugolnikov.docx | 167.48 КБ |
| kartochka.docx | 32.72 КБ |
| samostoyatelnaya_rabota.docx | 12.27 КБ |
Видео:8 класс, 22 урок, Первый признак подобия треугольниковСкачать

Предварительный просмотр:
Конспект урока по геометрии
Тема: «Признаки подобия треугольников».
УМК: Геометрия. 7 – 9 классы: учеб. для общеобразоват. организаций/ Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – 2-е изд. – М.: Просвещение, 2014. – 383 с.: ил.
образовательная: формирование умения применять признаки подобия треугольников при решении задач.
развивающая: развитие умения анализировать учебный материал, развитие умения слушать и вступать в диалог.
воспитательная: воспитание самостоятельности, внимательности, целеустремленности.
- повторить определение подобных треугольников;
- повторить изученные ранее признаки подобия треугольников;
- повторить алгоритм решения простейших задач на применение признаков подобия треугольников;
- повторить определение сходственных сторон;
- формировать умение решать задачи на применение признаков подобия треугольников;
- осуществить самоконтроль новых знаний.
личностные: формирование самооценки на основе успешной деятельности;
регулятивные: планировать своё действие в соответствии с поставленной задачей; умение оценивать правильность выполнения действия на уровне адекватной оценки;
коммуникативные: слушать и понимать речь других, вступать в диалог;
познавательные: ориентироваться в системе знаний; составлять ответы на вопросы.
Тип урока: комбинированный.
Оборудование: раздаточный материал (карточки с заданиями для самостоятельной работы в конце урока и для работы в классе).
- Организационный этап (1 мин).
- Актуализация знаний (3 мин).
- Этап закрепления новых знаний и способов действий (27 мин).
- Этап контроля и самоконтроля знаний и способов действий (5 мин).
- Подведение итогов урока (3 мин).
- Этап информации о домашнем задании (1 мин).
Цель: создать благоприятный психологический настрой на работу.
Форма работы: фронтальная.
личностные: планирование учебного сотрудничества с учителем и сверстниками;
регулятивные: прогнозирование своей деятельности;
коммуникативные: умение слушать и вступать в диалог;
познавательные: осознанное и произвольное построение речевого высказывания.
Фиксация отсутствующих на уроке.
Проверка подготовленности к уроку: наличие учебника, тетради, письменных принадлежностей.
Дежурные называют отсутствующих
Проверяют наличие учебных
Цель: актуализация опорных знаний и способов действий.
Форма работы: фронтальная.
регулятивные : выделение и осознание того, что уже пройдено;
коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли;
познавательные: поиск и выделение необходимой информации.
Прежде чем перейти к решению задач, давайте вспомним, чем мы занимались на прошлом уроке?
Какие треугольники называются подобными?
Верно. А какие стороны мы называем сходственными?
Сколько существует признаков подобия треугольников?
Два треугольника являются подобными, если … .
по первому признаку подобия:
по второму признаку подобия:
по третьему признаку подобия:
По какому алгоритму мы решали простейшие задачи на применение признаков подобия треугольников?
На прошлом уроке мы решали задачи на применение признаков подобия треугольников.
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Сходственными называются стороны, которые лежат напротив равных углов.
Существует три признака подобия треугольников.
два угла одного треугольника соответственно равны двух углам другого треугольника.
две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны.
три стороны одного треугольника пропорциональны трем сторонам другого треугольника.
Мы решали задачи по следующему алгоритму:
1. Доказать подобие треугольников;
2. Составить отношение сходственных сторон;
3. Найти из составленного отношения необходимую по условию задачи сторону.
- Этап закрепления знаний и способов действий.
Цель: обеспечение закрепления в памяти детей знаний и способов действий.
Форма работы: фронтальная, самостоятельная.
личностные: формирование математической компетентности;
регулятивные : планирование своей деятельности для решения поставленной задачи, контроль полученного результата;
коммуникативные: умение слушать и вступать в диалог, участие в коллективном обсуждении проблем;
познавательные: структурирование знаний.
Мы с вами повторили основные понятия предыдущих уроков.
А теперь откройте тетради, запишите число, классная работа и тему урока: Решение задач на тему «Признаки подобия треугольников».
У каждого на столе лежит карточка с задачами. Каждая карточка содержит 3 задачи.
Выполняем задания, сначала самостоятельно в тетради, потом сверяем решение и ответы:
На рисунке 1 FD || AB.
Найдите AC, если AB = 12 см,
FC = 2 см, FD = 3 см.
На рисунке 2 MN || KL. а) Докажите, что MO 

б) Найдите MO, если MN =10 см, KL = 24 см, MK = 17 см.
Найдите отношение площадей треугольников MKL и DEF, если
MK = 5 см, KL = 8 см, ML = 12 см, DE = 20 см, EF = 32 см, DF = 48 см.
Откройте учебник на странице 159, выполним номер 604 письменно.
№ 604 . Треугольники ABC и 


Назовите и запишите, что дано и что нужно найти. Сделайте чертеж к задаче.
Поиск решения задачи:
Что достаточно знать, чтобы найти стороны
Как мы можем найти коэффициент подобия двух треугольников?
Чему равен коэффициент подобия?
Теперь мы можем найти длины неизвестных сторон. Чему будут равны стороны
№562. В треугольнике ABC сторона AB равна а, а высота CH равна h . Найдите сторону квадрата, списанного в треугольник ABC так, что две соседние вершины квадрата лежат на стороне AB, а две другие – соответственно на сторонах АС и ВС.
Назовите и запишите, что дано и что нужно найти. Сделайте чертеж к задаче.
Записывают дату, классная работа и тему урока в тетрадь.
Внимательно читают условие задачи и решают ее в тетради.
Решают задачу самостоятельно в тетради.
Дано: ABC – треугольник, FD || AB, AB = 12 см, FC = 2 см, FD = 3 см.
1. 

То ΔCFD подобен ΔACB, по 2-м равным углам.
2. Составим отношения сходственных сторон:

3. Выберем те отношения данные в которых нам известны:




Решают задачу самостоятельно в тетради.
Дано: MNKL – трапеция, MN || KL, MN =10 см, KL = 24 см, MK = 17 см.
Доказать: MO 

1. 

То ΔMON подобен ΔLOK, по 2-м равным углам.
2. Составим отношения сходственных сторон:

Отсюда следует, что MO 

3. Выберем те отношения данные в которых нам известны:







Решают задачу самостоятельно в тетради.
Дано: MKL, DEF – треугольники, MK = 5 см, KL = 8 см, ML = 12 см, DE = 20 см, EF = 32 см, DF = 48 см.
Найти: 
1. Найдем отношения соответствующих сторон:



Следовательно, Δ MKL подобен Δ DEF, по трем сторонам, сходственные стороны пропорциональны.
2. Из п.1 следует, что 
Ответ: 
Решают задачу самостоятельно, один человек решает около доски.
Дано: ABC, 


Найти: 
Достаточно знать коэффициент подобия треугольников ABC и 
Коэффициент подобия треугольников ABC и 

Подставим известные длины сторон треугольников в отношение и получим:


Выберем те отношения, в которых встречаются необходимые нам стороны:




1. Т. к. ΔABC подобен Δ 



2.


3.


Ответ: 

Решают задачу самостоятельно, один человек решает около доски.
Дано: ABC – треугольник, AB = а , CH = h, MNFE– квадрат: ME 


1. NF || AB, т.к. MN || FE, а ME 
2. 

Следовательно, ΔABC подобен ΔNCF, по 2-м углам.
3. Составим отношение сходственных сторон:

4. MN=NF=FE=EM=x, т.к. MNFE – квадрат. Тогда CQ = h-x;
5. 
ah=(a+h)x; x= 
Следовательно, MN = 
Ответ: 
- Этап контроля и самоконтроля знаний и способов действий.
Цель: выявление качества и уровня усвоения знаний и способов действий.
Форма работы: индивидуальная.
личностные: формирование правильной самооценки; умения признавать собственные ошибки;
регулятивные : контроль, коррекция;
коммуникативные: поддержание здорового духа соперничества для поддержания мотивации учебной деятельности;
познавательные: применение полученных ранее знаний.
У каждого на столе лежат карточки с заданиями для самостоятельной работы.
Всего два варианта, каждая карточка включает в себя одну задачу. Выполняем письменно в тетрадях.
На выполнения этого задания у вас 5 минут.
Высота CD прямоугольного треугольника ABC делит
гипотенузу АВ на части AD = 16 см и BD = 9 см. Докажите, что ΔACD подобен ΔCBD, и найдите высоту CD.
📹 Видео
8 класс, 23 урок, Второй признак подобия треугольниковСкачать

Геометрия 8 класс (Урок№15 - Признаки подобия треугольников.)Скачать

Геометрия 8 класс. Третий признак подобия треугольниковСкачать

ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ Атанасян 553 555 558 562Скачать

Геометрия 8 класс. Второй признак подобия треугольниковСкачать

Первый признак подобия треугольников. Доказательство. 8 класс.Скачать

63. Третий признак подобия треугольниковСкачать

ПОДОБИЕ ТРЕУГОЛЬНИКОВ 8 класс ЗАДАЧИ АтанасянСкачать

Самостоятельная работа 9 | Геометрия | 8 класс | Признаки подобия треугольников | Подробный разборСкачать

Второй признак подобия треугольников. Доказательство. 8 класс.Скачать

Задание № 551 — Геометрия 8 класс (Атанасян)Скачать

Геометрия 8 класс : Признаки подобия треугольниковСкачать

Признаки подобия треугольниковСкачать

8 класс, 20 урок, Определение подобных треугольниковСкачать

Первый признак подобия треугольников - геометрия 8 классСкачать