Апофема в равнобедренном треугольнике

Для решения задач на обширную тему «Стереометрия» нужно выучить и разобрать очень много элементов и тонкостей, полностью изучить все свойства фигур, а также не забывать свойства всех фигур, которые включены в курс «Планиметрии».

Среди задач по объемным фигурам очень часто встречается правильная пирамида, чтобы легко решать их, нужно хорошо с ней познакомиться. Пирамида называется правильной, если в ее основании лежит правильный многоугольник, а ее вершина спроецирована в центр основания. Как раз при изучении этого многоугольника вы услышите об апофеме.

Как вы уже поняли, в геометрии понятие апофемы — это широко распространенное явление. Невозможно узнать некоторые измерения пирамиды без знания этого. Само слово «апофема» — это пришедшее к нам из греческого языка явление, и переводится оно как «откладываю».

Видео:№119. В равнобедренном треугольнике DEK с основанием DK=16см отрезок EF— биссектриса,Скачать

Определение

В планиметрии апофема — перпендикуляр (как сам, так и его длина), который проведен к стороне правильного многоугольника из центра. В стереометрии апофема пирамиды — это высота в боковой грани, которая проведена к основанию. Используется только для правильных пирамид. Соответственно, апофема правильной треугольной пирамиды — это высота ее грани, которая представлена равнобедренным треугольником.

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Какова роль апофемы

Апофема — это очень важный элемент пирамиды, потому что с ее помощью можно решить огромное количество задач. В частности, боковая поверхность правильной пирамиды равна полупроизведению периметра основания и апофемы грани.

S_бп = (P_осн*h)/2; h — апофема, это ее ключевая роль.

Не путайте с H (высота объемной фигуры в стереометрии).

Также, благодаря знанию апофемы, можно найти площадь грани как равнобедренного треугольника.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Свойства апофемы

Их мало, но все же их нужно помнить. В целом это следствия, вытекающие из определения. Итак, апофема в правильной пирамиде:

1. Опущена на сторону основания под углом 90 градусов.
2. Делит сторону, на которую опущена, пополам, так как является высотой в равнобедренном/равностороннем треугольнике и по совместительству — медианой.

В правильной пирамиде все апофемы равны, так как все ее боковые грани также одинаковые. При нахождении длины апофемы вам придется воспользоваться как свойствами многоугольника, так и свойствами многогранника. Как же найти числовое значение апофемы в правильной пирамиде?

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Как найти апофему пирамиды

Ее можно найти, применяя все ранее полученные знания, вот всего лишь несколько примеров:

• Если известны боковое ребро и сторона основания. Так как апофема делит сторону основания пополам и образует с ней угол в 90 градусов, то найти ее из прямоугольного треугольника по теореме Пифагора вам не составит труда. Также можно найти апофему, используя знания соотношений в прямоугольном треугольнике.
• Если известен радиус вписанной окружности в основание правильной пирамиды и высота всей фигуры. Радиус, проведенный к точке касания, перпендикулярен касательной, и апофема перпендикулярна этой стороне основания (которая является касательной к вписанной окружности). Высота фигуры перпендикулярна основанию и попадает в центр окружности, вписанной в основание пирамиды. Следовательно, радиус и высота фигуры являются катетами и образуют прямой угол, а вместе с апофемой — прямоугольный треугольник. И опять же по теореме Пифагора или через соотношения в прямоугольном треугольнике вы легко найдете апофему.

• Также если дана площадь грани и известно основание.

В любом случае при нахождении апофемы вам придется вспоминать все основные законы и правила планиметрии. Если неизвестны какие-то элементы из этого списка, то вы можете оперировать данными параметрами, и, постепенно находя вышеописанные данные, найти апофему вам не составит труда. Надеемся, что наша статья помогла вам в освоении такой интересной темы.

Видео:Равнобедренный треугольник. 7 класс.Скачать

Апофема пирамиды. Формулы для апофемы правильной треугольной пирамиды

Пирамида — это пространственный полиэдр, или многогранник, который встречается в геометрических задачах. Основными свойствами этой фигуры являются ее объем и площадь поверхности, которые вычисляются из знания любых двух ее линейных характеристик. Одной из таких характеристик является апофема пирамиды. О ней пойдет речь в статье.

Видео:Апофема правильной пирамиды. Задание А2 из ЦТ 2020 #цт2020Скачать

Фигура пирамида

Прежде чем приводить определение апофемы пирамиды, познакомимся с самой фигурой. Пирамида представляет собой многогранник, который образован одним n-угольным основанием и n треугольниками, составляющими боковую поверхность фигуры.

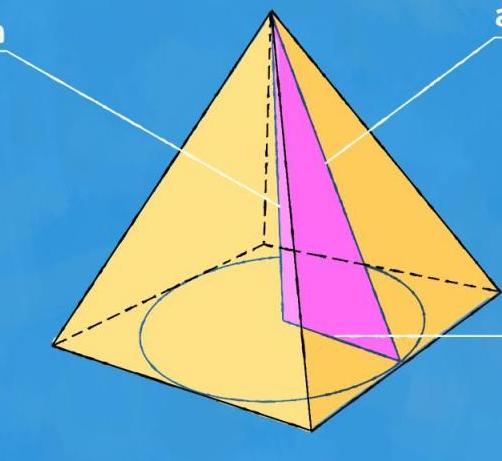
Всякая пирамида имеет вершину — точку соединения всех треугольников. Перпендикуляр, проведенный из этой вершины к основанию, называется высотой. Если высота пересекает в геометрическом центре основание, то фигура называется прямой. Пирамида прямая, имеющая равностороннее основание, называется правильной. На рисунке показана пирамида с шестиугольным основанием, на которую смотрят со стороны грани и ребра.

Видео:Пирамида. 11 класс.Скачать

Апофема правильной пирамиды

Ее также называют апотемой. Под ней понимают перпендикуляр, проведенный из вершины пирамиды к стороне основания фигуры. По своему определению этот перпендикуляр соответствует высоте треугольника, который образует боковую грань пирамиды.

Поскольку мы рассматриваем пирамиду правильную с n-угольным основанием, то все n апофем для нее будут одинаковыми, поскольку таковыми являются равнобедренные треугольники боковой поверхности фигуры. Заметим, что одинаковые апофемы являются свойством правильной пирамиды. Для фигуры общего типа (наклонной с неправильным n-угольником) все n апофем будут разными.

Еще одним свойством апофемы пирамиды правильной является то, что она одновременно является высотой, медианой и биссектрисой соответствующего треугольника. Это означает, что она делит его на два одинаковых прямоугольных треугольника.

Видео:№255. В равнобедренном треугольнике CDE с основанием СЕ проведена высота CF.Скачать

Треугольная пирамида и формулы для определения ее апофемы

В любой правильной пирамиде важными линейными характеристиками являются длина стороны ее основания, ребро боковое b, высота h и апофема h_b. Эти величины друг с другом связаны соответствующими формулами, которые можно получить, если начертить пирамиду и рассмотреть необходимые прямоугольные треугольники.

Правильная треугольная пирамида состоит из 4 треугольных граней, причем одна из них (основание) должна быть обязательно равносторонней. Остальные являются равнобедренными в общем случае. Апофему треугольной пирамиды можно определить через другие величины по следующим формулам:

Первое из этих выражений справедливо для пирамиды с любым правильным основанием. Второе выражение характерно исключительно для треугольной пирамиды. Оно показывает, что апофема всегда больше высоты фигуры.

Не следует путать апофему пирамиды с таковой для многогранника. В последнем случае апофемой называется перпендикулярный отрезок, проведенный к стороне многогранника из его центра. Например, апофема равностороннего треугольника равна √3/6*a.

Видео:№109. В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AMСкачать

Задача на вычисление апофемы

Пусть дана правильная пирамида с треугольником в основании. Необходимо вычислить ее апофему, если известно, что площадь этого треугольника равна 34 см 2 , а сама пирамида состоит из 4 одинаковых граней.

В соответствии с условием задачи мы имеем дело с тетраэдром, состоящим из равносторонних треугольников. Формула для площади одной грани имеет вид:

Откуда получаем длину стороны a:

Для определения апофемы h_b воспользуемся формулой, содержащей боковое ребро b. В рассматриваемом случае его длина равна длине основания, имеем:

Подставляя значение a через S, получим конечную формулу:

Мы получили простую формулу, в которой апофема пирамиды зависит только от площади ее основания. Если подставить значение S из условия задачи, то получим ответ: h_b ≈ 7,674 см.

Видео:Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | АлгебраСкачать

Пирамида

Пирамида – многогранник, основание которого — многоугольник , а остальные грани — треугольники, имеющие общую вершину.

По числу углов основания различают пирамиды треугольные , четырёхугольные и т. д.

Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.

Основание — многоугольник, которому не принадлежит вершина пирамиды.

Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.

Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).

Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Некоторые свойства пирамиды

1) Если все боковые ребра равны, то

– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр

– боковые ребра образуют с плоскостью основания равные углы

Верно и обратное.

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

2) Если все грани пирамиды наклонены к плоскости основания под одним углом , то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр

Верно и обратное.

Видео:Нахождение апофемы пирамидыСкачать

Виды пирамид

Пирамида называется правильной , если основанием её является правильный многоугольник, а вершина проецируется в центр основания.

Для правильной пирамиды справедливо:

– боковые ребра правильной пирамиды равны;

– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;

– в любую правильную пирамиду можно вписать сферу;

– около любой правильной пирамиды можно описать сферу;

– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Видео:№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

Пирамида называется прямоугольной , если одно из боковых рёбер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.

🎦 Видео

Равнобедренный треугольник. Практическая часть. 7 класс.Скачать

Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать

Вещдок (HD): расследование дела "Равнобедренный треугольник"Скачать

Свойства равнобедренного треугольника. 7 класс.Скачать

№ 119 - Геометрия 7-9 класс АтанасянСкачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

№ 107 - Геометрия 7-9 класс АтанасянСкачать