Определить видимость пересечения треугольников (5 видео)

Определение видимости на чертеже.

В начертательной геометрии плоскости считаются непрозрачными, поэтому необходимо на проекциях определить видимость.

Для определения видимости на чертеже используем метод конкурирующих точек, сущность которого заключается в выборе двух скрещивающихся прямых.

Для определения видимости на фронтальной плоскости проекций V поступают так. Выбираем две скрещивающиеся прямые В²С² и М²N², фронтальные проекции которых пересекаются в точках 1 и 3. По горизонтальной проекции определяем, что проекция точки 3¢, лежащая на проекции прямой M¢N¢, будет закрывать проекцию точки 1¢, лежащую на проекции прямой В¢С¢, т. к она будет ближе к наблюдателю. На чертеже направление взгляда наблюдателя показано стрелкой. Следовательно, на фронтальной плоскости проекций проекция М²N² будет закрывать проекцию В²С². Границей видимости является проекция точки пересечения К².

Для определения видимости на горизонтальной плоскости проекций Н выбираем две скрещивающиеся прямые А¢С¢ и M¢N¢, горизонтальные проекции которых пересекаются в точках 4¢ и 5¢. По фронтальной проекции определяем, что проекция точки 5², лежащая на проекции прямой М²N², будет закрывать проекцию точки 4², лежащую на проекции прямой А²С², т. к. она будет ближе к наблюдателю. На чертеже направление взгляда наблюдателя показано стрелкой. Следовательно, на горизонтальной плоскости проекций проекция M¢N¢ будет закрывать проекцию А¢С¢. Границей видимости является проекция точки пересечения К¢.

Задача 3. Построение линии пересечения двух плоскостей, одна из которых занимает частное положение.

Даны две плоскости: плоскость ∆АВС – плоскость общего положения, плоскость ∆DЕК – плоскость частного положения, которая расположена перпендикулярно фронтальной плоскости проекций (рис. 3).

Рис. 3. Построение линии пересечения двух плоскостей, одна из которых занимает
частное положение

Фронтальная проекция ∆DЕК совпадает с фронтальным следом плоскости и фронтальной проекцией линии пересечения треугольников.

(KL) ‑ линия пересечения двух треугольников. Проекции этой линии пересечения – фронтальную и горизонтальную строят исходя из свойства принадлежности точек K и L сторонам (АВ) и (ВС), соответственно. Видимость треугольников на горизонтальной плоскости проекций определяем методом конкурирующих точек, рассмотренном в задаче 2.

Задача 4. Построение линии пересечения двух плоскостей общего положения.

Даны две плоскости общего положения, заданные треугольниками АВС и DЕК. Построить линию пересечения двух треугольников, определить видимость треугольников на проекциях.

Прямая линия, получаемая при взаимном пересечении двух плоскостей, определяется двумя точками, каждая из которых одновременно принадлежит обеим плоскостям. Общие точки определяются решением основной позиционной задачи начертательной геометрии – построение точки пересечения прямой с плоскостью (см. рис. 2).

Для решения данной задачи проводят вспомогательные плоскости-посредники частного положения (проецирующие плоскости). Решение задачи приведено на рис. 4.

Алгоритм решения задачи:

1. Определяют первую точку линии пересечения двух треугольников – точку М.

1.1. Фронтально-проецирующая плоскость a проведена через сторону DК и задана на чертеже фронтальным следом a_V.

1.2. Плоскость a пересекает плоскость треугольника АВС по прямой (1,2), на чертеже строят две проекции этой прямой.

1.3. Прямая (1,2) пересекает сторону DК в точке М, строят две проекции точки М² и М¢.

2. Определяют вторую точку искомой линии пересечения двух треугольников – точку N.

2.1. Горизонтально-проецирующая плоскость b проведена через сторону АВ и задана на чертеже горизонтальным следом b_Н.

2.2. Плоскость b пересекает плоскость треугольника DЕК по прямой (3,4), на чертеже строят две проекции этой прямой.

2.3. Прямая (3,4) пересекает АВ в точке N, строят две проекции точки N² и N¢.

Плоскости треугольников АВС и DЕК пересекаются по прямой MN.

Рис. 4. Построение линии пересечения двух треугольников

3. Видимость плоских фигур на проекциях определяют методом конкурирующих точек.

Для определения видимости на фронтальной плоскости проекций V выбираем две скрещивающиеся прямые D²K² и A²B², фронтальные проекции которых пересекаются в точках 1² и 5². По горизонтальной проекции определяем, что проекция точки 5¢, лежащая на проекции прямой D¢K¢, будет закрывать проекцию точки 1¢, лежащую на проекции прямой А¢В¢, т. к. она будет ближе к наблюдателю. Следовательно, на фронтальной плоскости проекция D²K² будет закрывать проекцию A²B². Границей видимости является проекция линии пересечения M²N².

Для определения видимости на горизонтальной плоскости проекций Н выбираем две скрещивающиеся прямые А¢В¢ и D¢Е¢, горизонтальные проекции которых пересекаются в точках 3¢ и 6¢. По фронтальной проекции определяем, что проекция точки 3², лежащая на проекции прямой D²Е², будет закрывать проекцию точки 6², лежащую на проекции прямой A²B², т.к. она будет ближе к наблюдателю. Следовательно, на горизонтальной плоскости проекция D¢Е¢ будет закрывать проекцию А¢В¢. Границей видимости является проекция линии пересечения N¢M¢.

Задача 5. Построить две проекции линии пересечения плоскости a ‑ общего положения, заданной следами и плоскости b ‑ общего положения, заданной параллельными прямыми а и b.

Для решения данной задачи проводят вспомогательные плоскости-посредники частного положения (плоскости уровня), пересекающие заданные плоскости по прямым, недостающие проекции которых легко строятся и пересекаются в пределах чертежа.

Графическое решение задачи приведено на рис. 5.

Рис. 5. Построение линии пересечения двух плоскостей

Вспомогательная горизонтальная плоскость-посредник γ задана следом γ_V и пересекает плоскость a по горизонтали, проходящей через точку 3, а плоскость b по горизонтали (1, 2). Горизонтальные проекции этих горизонталей пересекаются в точке К. Строят фронтальную проекцию точки К, используя свойство принадлежности точки прямой линии. Точка К принадлежит обеим плоскостям a и b. Вторая точка N, общая для двух плоскостей a и b, определяется второй вспомогательной плоскостью-посредником частного положения δ (на чертеже задана следом δ_V). Искомая прямая (КN) является линией пересечения двух плоскостей a и b.

ПРИЛОЖЕНИЕ 1

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Гордон В.О., Семенцов-Огиевский М. А. Курс начертательной геометрии. Учеб. пособие. М.: Высшая школа. 2007.272 с.

2. Самохвалов Ю. И. Начертательная геометрия. Учебное пособие. Екатеринбург: Изд-во УГГУ. 2011. 121 с.

3. Самохвалов Ю. И., Шангина Е. И. Начертательная геометрия. Инженерная графика. Учебно-методическое пособие. Екатеринбург: Изд-во УГГУ. 2011. 96 с.

Видео:Построить линию пересечения треугольников ABC и DEF. Определить видимость. Вариант 2Скачать

Построить линию пересечения треугольников ABC и EDK и показать видимость их в проекциях.
Определить натуральную величину треугольника ABC.

1. Строим проекции треугольника АВС.

2. Строим проекции треугольника EDK.

3. Находим точку пересечения стороны АС с треугольником EDK

4. Находим точку пересечения стороны А B с треугольником EDK и строим линию пересечения MN

5. С помощью конкурирующих точек 4 и 5 определяем видимость треугольников на фронтальной плоскости проекций.

6. С помощью конкурирующих точек 6 и 7 определяем видимость треугольников на горизонтальной плоскости проекций.

7. В треугольнике ABC проводим горизонталь CL и плоскопараллельным перемещением относительно горизонтальной плоскости проекций располагаем горизонталь перпендикулярно фронтальной плоскости проекций.

Строим фронтальную проекцию треугольника ABC . Треугольник должен проецироваться в прямую линию.

8. Определяем действительную величину треугольника ABC и строим на нем линию пересечения MN.

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Определение видимости в начертательной геометрии с примерами

Определение видимости:

Точки, расположенные на одной проецирующей прямой, называются конкурирующими.

Точки, расположенные на одной горизонтально-проецирующей прямой, называются конкурирующими относительно горизонтальной плоскости проекций. Из двух точек A и B (рис. 7.1,а), конкурирующих на горизонтальной проекций, видима та, высота которой больше (B-видима, A-плоскости невидима).

Рис. 7.1. Конкурирующие точки:
а — относительно горизонтальной плоскости проекций;
б — относительно фронтальной плоскости проекций

Точки, расположенные на одной фронтально-проецирующей прямой, называются конкурирующими относительно фронтальной плоскости проекций. Из двух точек C и D (рис. 7.1,б), конкурирующих относительно фронтальной плоскости проекций, видима та точка, у которой больше глубина (C- видима, D — невидима).

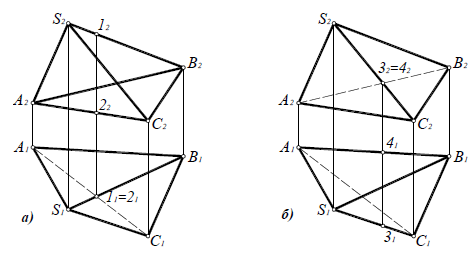
Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 7.2).

Рис. 6.17. Определение видимости ребер тетраэдра на комплексном чертеже:
а — относительно горизонтальной плоскости проекций;
б — относительно фронтальной плоскости проекций

Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 7.2,а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1 ∈ SB и 2 ∈ACявляются конкурирующими на П₁, поскольку находятся на горизонтально-проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П₁, следовательно, видимо и реброSB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABCневидима на П₁.

Видимость на фронтальной проекции (рис. 7.2,б) определяется с помощью конкурирующих точек 3 ∈ SCи 4 ∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SCна фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы на П₂.

Рекомендую подробно изучить предметы:

Инженерная графика
Начертательная геометрия
Компас
Автокад
Черчение
Проекционное черчение
Аксонометрическое черчение
Строительное черчение
Техническое черчение
Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

Конструктивное отображение пространства
Чертежи точки, отрезка прямой
Чертежи плоскости
Взаимное положение двух плоскостей, прямой линии и плоскости
Пересечение поверхностей вращения плоскостью
Виды, разрезы, сечения
Геометрические тела
Комплексный чертеж

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.