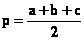Вычисление площадей и периметров фигур

треугольника по данным трем сторонам,
прямоугольника по данным ширине и высоте,
круга по заданному радиусу.

Длины сторон и радиус вводятся пользователем.

Площади и периметры фигур можно найти по следующим формулам.

Периметр треугольника: P = a + b + c
Площадь треугольника: S = √(p(p-a)(p-b)(p-c)), где p = P/2

Периметр прямоугольника: P = 2(a + b)
Площадь прямоугольника: S = ab

Периметр круга: P = 2πr
Площадь круга: S = πr 2

Содержание

Pascal
Язык Си
Python
КуМир
Basic-256
Площадь треугольника по формуле Герона на Питоне
Математическая часть задачи
Решение задачи на Питоне
Второй вариант решения задачи
Третий вариант решения задачи
Алгоритм вычисления площади треугольника информатика
📹 Видео

Видео:Вычисление площади треугольника через основание и высоту в программе на языке ПаскальСкачать

Pascal

вычислить площадь фигуры паскаль

Видео:Программа вычисления площади треугольника на языке Си.Скачать

Язык Си

В библиотеке math.h нет константы числа π.

При компиляции с помощью gcc необходимо в конце команды указать ключ -lm (из-за math.h).

Видео:Решение простых задач на python | Площадь и периметр прямоугольного треугольникаСкачать

Python

вычислить площадь фигуры Python

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

КуМир

Не нашлось константы для числа π

Видео:Найти площадь прямоугольника, треугольника или круга. Решение задачи на PythonСкачать

Basic-256

Total 0
0
0
0
0

вычислить площадь фигуры паскаль

var
a,b,c: word;
w,h: word;
r: word;
P,S: real;
begin
readln(a,b,c);
P := (a + b + c) / 2;
S := sqrt(P * (P — a) * (P — b) * (P — c));
writeln(‘P=’,a+b+c,’; S=’,S:5:2);

readln(r);
P := 2 * pi * r;
S := pi * r * r;
writeln(‘P=’,P:5:2,’; S=’,S:5:2);
end.

5 3 5
P=13; S= 7.15
3 9
P=24; S=27
5
P=31.42; S=78.54

#define PI 3.14159

main() <
int a,b,c;
float p,S;
printf(«Длины сторон треугольника: «);
scanf(«%d%d%d», &a,&b,&c);
p = (a+b+c)/2;
S = sqrt(p*(p-a)*(p-b)*(p-c));
printf(«P = %d; S = %.2fnn», (a+b+c), S);
printf(«Ширина и высота прямоугольника: «);
scanf(«%d%d», &a,&b);
printf(«P = %d; S = %dnn», (a+b)*2, a*b);
printf(«Радиус круга: «);
scanf(«%d», &a);
printf(«P = %.2f; S = %.2fn», 2*PI*a, PI*pow(a,2));
>

Длины сторон треугольника: 4 4 6
P = 14; S = 7.94

Ширина и высота прямоугольника: 2 5
P = 14; S = 10

Радиус круга: 3
P = 18.85; S = 28.27

В библиотеке math.h нет константы числа π.

При компиляции с помощью gcc необходимо в конце команды указать ключ -lm (из-за math.h).

вычислить площадь фигуры Python

print(«Введите длины сторон треугольника: «)
a = int(input(«a=»))
b = int(input(«b=»))
c = int(input(«c=»))
p = (a+b+c)/2
s = math.sqrt(p*(p-a)*(p-b)*(p-c))
print(«P=%d; S=%.2f» % (a+b+c, s))

print(«Введите длины сторон прямоугольника: «)
a = int(input(«a=»))
b = int(input(«b=»))
print(«P=%d; S=%d» % ((a+b)*2, a*b))

print(«Введите радиус круга: «)
r = int(input(«r=»))
print(«P=%.2f; S=%.2f» % (2*math.pi*r, math.pi*r**2))

Введите длины сторон треугольника:
a=2
b=4
c=3
P=9; S=2.90
Введите длины сторон прямоугольника:
a=6
b=7
P=26; S=42
Введите радиус круга:
r=3
P=18.85; S=28.27

алг фигуры
нач
цел a,b,c
ввод a, b, c
вещ p, S
p := (a+b+c)/2
S := sqrt(p*(p-a)*(p-b)*(p-c))
вывод «P=», p*2, «; S=», S, нс

цел w, h
ввод w, h
вывод «P=», (w+h)*2, «; S=», w*h, нс

цел r
ввод r
p := 2 * 3.14 * r
S := 3.14 * r**2
вывод «P=», p, «; S=», S, нс
кон

5 7 9
P=21; S=17.41228
4 9
P=26; S=36
5
P=31.4; S=78.5

Не нашлось константы для числа π

# найти площади и периметры геометрических фигур
decimal 2
# треугольник
print «ТРЕУГОЛЬНИК»
input » первая сторона: «, a
input » вторая сторона: «, b
input » третья сторона: «, c
p = a + b + c
print «Периметр: » + p
p = p / 2
s = sqr(p*(p-a)*(p-b)*(p-c))
print «Площадь: » + s
print
# прямоугольник
print «ПРЯМОУГОЛЬНИК»
input » ширина: «, a
input » высота: «, b
print «Периметр: » + ((a + b) * 2)
print «Площадь: » + (a * b)
print
# круг
print «КРУГ»
input » радиус: «, r
print «Периметр: » + (2 * pi * r)
print «Площадь: » + (pi * r^2)

ТРЕУГОЛЬНИК
первая сторона: 5
вторая сторона: 5
третья сторона: 5
Периметр: 15
Площадь: 10.83

ПРЯМОУГОЛЬНИК
ширина: 5
высота: 5
Периметр: 20
Площадь: 25

КРУГ
радиус: 5
Периметр: 31.42
Площадь: 78.54

Площадь треугольника по формуле Герона на Питоне

На языке программирования Питон можно решить много разных задач, в том числе и по математике. Для начинающих изучать этот язык будет полезно решить задание на вычисление площади треугольника. Одним из способов вычисления этой величины является применение формулы Герона.

Видео:Уроки программирования на языке Pascal. Вычисление площади треугольника по координатам вершинСкачать

Математическая часть задачи

Из школьного курса математики вы знаете, что площадь треугольника можно вычислить по данным длинам трёх его сторон по формуле Герона:

p – полупериметр треугольника.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Решение задачи на Питоне

На вход программе подаются целые числа, выводом программы должно являться вещественное число, соответствующее площади треугольника.

Для ввода целых чисел используем функцию int() .

Для решения задачи нам необходимо подключить библиотеку с математическими функциями. Делаем это с помощью строки импорта:

Функция для извлечения квадратного корня в этой библиотеке записывается так:

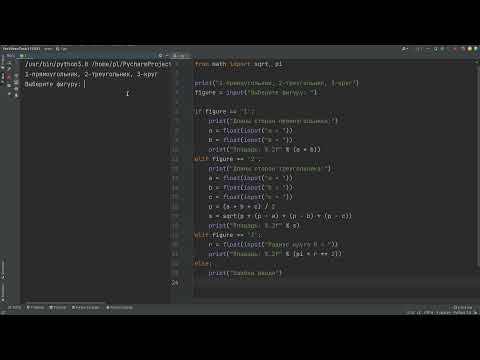
Код программы для вычисления площади треугольника

Результат выполнения кода программы

Видео:Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

Второй вариант решения задачи

Также можно воспользоваться стандартной функцией возведения числа в степень. Дело в том, что квадратный корень — это возведение в степень 1/2.

Синтаксис функции такой:

где x — число, возводимое в степень, а y — сама степень.

Вот так это запишется по формуле:

Результат выполнения кода:

Видео:Вычисление площади треугольника по координатам его вершин. | Задачи C#Скачать

Третий вариант решения задачи

Вместо извлечения корня можно возвести в степень 1/2 или 0,5 . При этому функцию использовать не нужно.

Как видим, результат выполнения программы точно такой же.

Видео:Нахождение площади треугольника в С++Скачать

Алгоритм вычисления площади треугольника информатика

6.2. ОСНОВНЫЕ ТИПЫ ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТМОВ

Наиболее простым видом алгоритма является линейный алгоритм, при котором действия выполняются последовательно, одно за другим, без разветвлений и возвратов.

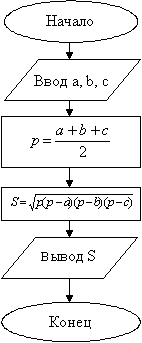
Пример . Вычисление площади треугольника по трем сторонам a , b , c по формуле Герона:

, где

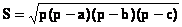
Блок-схема алгоритма имеет вид:

В процессе решения многих задач часто возникает необходимость в зависимости от исходных данных или получающихся промежуточных результатов проводить вычисления либо по одним, либо по другим формулам, т.е. по разным направлениям – ветвям. Такой вычислительный алгоритм называется разветвляющимся.

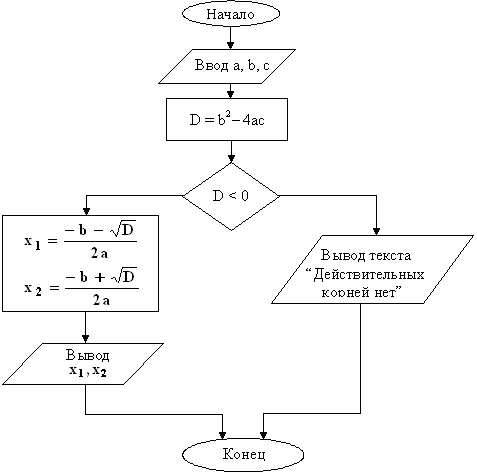
Пример. Нахождение действительных корней квадратного уравнения

Блок-схема алгоритма имеет вид:

При решении большинства практических задач возникает необходимость неоднократного повторения однотипных действий при различных значениях параметров, определяющих эти действия. Такие алгоритмы называются циклическими, а повторяемые участки вычислений – циклами.

Пример . Вычисление факториала натурального числа