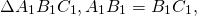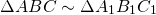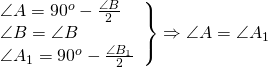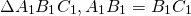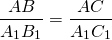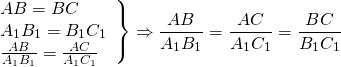Любые два равнобедренных треугольника равны

Какие из следующих утверждений верны?

1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.

2) Любые два равнобедренных треугольника подобны.

3) Любые два прямоугольных треугольника подобны.

4) Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.»— верно, по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.

2) «Любые два равнобедренных треугольника подобны.» — неверно, так как углы, заключенные между пропорциональными сторонами, не равны.

3) «Любые два прямоугольных треугольника подобны.» — неверно, так как нет второго равного угла.

4) «Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.» — неверно, треугольник с такими сторонами является прямоугольным.

Видео:№159. Докажите, что два равнобедренных треугольника равны, если боковая сторона и угол, противолежащСкачать

Задание №20 ОГЭ по математике

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Анализ геометрических высказываний

В 20 задании из приведенных утверждений необходимо выбрать одно или несколько правильных. Утверждения из общего теоретического курса геометрии, поэтому, какие-то определенные рекомендации здесь дать нельзя, кроме как полного повторения теоретического курса. Другое дело, что если вы точно не знаете какое-либо утверждение, то решить задачу можно наоборот — выбирая и отсеивая неправильные. Это задание не имеет какого либо подхода к решению, однако ниже я привел несколько разобранных задач.

Разбор типовых вариантов задания №20 ОГЭ по математике

Первый вариант задания

Какие из следующих утверждений верны?

1. Все диаметры окружности равны между собой.
2. Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3. Любые два равносторонних треугольника подобны.

Решение:

Все диаметры окружности всегда равны между собой — это даже интуитивно понятно. Что касается второго утверждения, то оно неверно — вписанный угол всегда в два раза меньше центрального. А вот третье утверждение тоже верно — треугольники могут быть подобны по трем углам, а у равносторонних треугольников они всегда равны.

Второй вариант задания

Какие из следующих утверждений верны?

1. Все высоты равностороннего треугольники равны.
2. Существуют три прямые, которые проходят через одну точку.
3. Если диагонали параллелограмма равны, то он является ромбом.

Решение:

Первое утверждение верно, так как у равностороннего треугольника все стороны равнозначны, а значит и все элементы, проведенные к ним, тоже. Второе утверждение тоже верно, так как нет ограничений на количество произвольных прямых, проходящих через одну точку. Третье утверждение неверно — если диагонали равны, то это либо прямоугольник, либо квадрат.

Третий вариант задания

Какие из следующих утверждений верны?

1. Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
2. Любой прямоугольник можно вписать в окружность.
3. Через заданную точку плоскости можно провести единственную прямую.

Решение:

Первое утверждение верно из общих свойств треугольника — сумма двух сторон всегда больше третьей. Второе утверждение тоже верно — действительно, любой прямоугольник можно вписать в окружность. Третье утверждение неверно, так как я писал уже чуть выше, что нет ограничений на количество произвольных прямых, проходящих через одну точку.

Демонстрационный вариант ОГЭ 2019

Укажите номера верных утверждений.

1. Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2. Треугольник со сторонами 1, 2, 4 существует.
3. Если в ромбе один из углов равен 90° , то такой ромб — квадрат.
4. В любом параллелограмме диагонали равны.

Решение:

Проанализируем каждое из утверждений:

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

Да, такое утверждение в геометрии есть, с дополнением » и только одну» :

«Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой, и причем только одну.»

2) Треугольник со сторонами 1, 2, 4 существует.

Для существования треугольника должно выполняться следующее правило:

Сумма двух сторон всегда больше третьей. В данном случае это не так, так как 1 + 2

Четвертый вариант задания

Какое из следующих утверждений верно?

1) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом.

2) Смежные углы всегда равны.

3) Каждая из биссектрис равнобедренного треугольника является его высотой.

Решение:

Проанализируем каждое утверждение.

1) Это утверждение верно, поскольку равенство и перпендикулярность диагоналей является одним из свойств именно квадрата.

2) Это утверждение неверно. Основание – соответствующая теорема, которой утверждается, что смежные углы в сумме имеют 180 0 , т.е. дополняют друг друга до развернутого угла. Следовательно, равенство смежных углов может иметь место только в случае, если достоверно известно, что один из них прямой.

3) Утверждение неверно. Высотой является только биссектриса, опущенная на основание равнобедренного треугольника.

Пятый вариант задания

Какое из следующих утверждений верно?

1) Если угол острый, то смежный с ним угол также является острым.

2) Если диагонали параллелограмма перпендикулярны, то этот параллелограмм является ромбом.

3) Касательная к окружности параллельна радиусу, проведённому в точку касания.

Решение:

Выполняем анализ утверждений.

1) Согласно теореме о смежных углах, их сумма всегда равна 180 0 . Это означает, что любой из смежных углов является разностью 180 0 и величины 2-го смежного угла. Если первый смежный угол острый, значит, второй равен разности 180 0 и острого угла (т.е. угла, меньшего 90 0 ), которая в любом случае окажется больше 90 0 . А угол, больший 90 0 , по определению тупой. Итак, утверждение неверно.

2) Одно из свойств ромба заключается в том, что его диагонали перпендикулярны. Однако и диагонали квадрата тоже пересекаются под прямым углом. Но поскольку квадрат является частным случаем ромба, то и в этом противоречия заданному утверждению нет. Т.е. в целом утверждение верно.

3) Одно из основных св-в касательных к окружности заключается в том, что касательная всегда перпендикулярна к радиусу, проведенному из центра этой окружности в точку касания. Оно противоречит заданному утверждению, поэтому утверждение неверно.

Видео:Любые два равносторонних треугольника подобны. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Равнобедренные треугольники подобны

Выясним, в каких случаях равнобедренные треугольники подобны.

Признаки подобия равнобедренных треугольников

1) Если угол между боковыми сторонами одного равнобедренного треугольника равен углу между боковыми сторонами другого равнобедренного треугольника, то такие треугольники подобны.

Дано : ∆ ABC, AB=BC,

Из равенства углов при вершине равнобедренных треугольников следует равенство их углов при основаниях:

Следовательно, треугольники ABC и A1B1C1 подобны по двум углам.

Что и требовалось доказать .

2) Если угол между основанием и боковой стороной одного равнобедренного треугольника равен углу между между основанием и боковой стороной другого равнобедренного треугольника, то такие треугольники подобны.

Дано : ∆ ABC, AB=BC,

Так как углы при основании равнобедренного треугольника равны, в треугольнике ABC ∠A=∠C, в треугольнике A1B1C1∠A1=∠C1. Следовательно, треугольники ABC и A1B1C1 подобны по двум углам.

Что и требовалось доказать .

3) Если основание и боковая сторона одного равнобедренного треугольника пропорциональны основанию и боковой стороне другого равнобедренного треугольника, то такие треугольники подобны.

Дано : ∆ ABC, AB=BC,

Следовательно, треугольники ABC и A1B1C1 подобны по трём сторонам.

📽️ Видео

Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать

Признаки равенства треугольников. 7 класс.Скачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

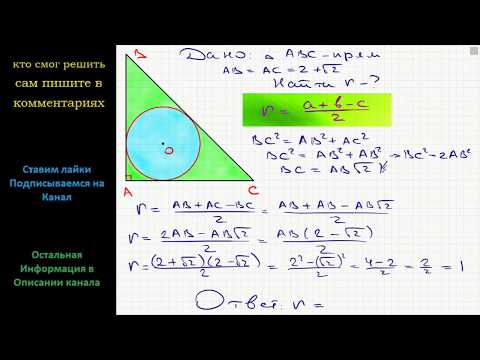
Геометрия Катеты равнобедренного прямоугольного треугольника равны 2+√2. Найдите радиус окружностиСкачать

№561. Докажите, что два равносторонних треугольника подобны.Скачать

Геометрия Докажите, что два равнобедренных треугольника подобны, если углы при их вершинах равныСкачать

№134. Докажите, что равнобедренные треугольники равны, если основание и прилежащий кСкачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Равнобедренный треугольник. 7 класс.Скачать

№250. Найдите сторону равнобедренного треугольника, если две другие стороны равны: а) 7 см и 3 смСкачать

Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

№252. Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 74 смСкачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Первый признак равенства треугольников. 7 класс.Скачать