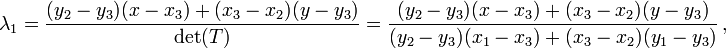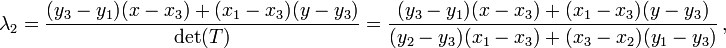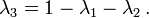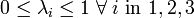Алгоритм растеризации треугольника с (3 видео)

Алгоритм растеризации треугольника с

Содержание

Друзья
Растеризация треугольника. Алгоритм заливки (заполнения)
Программирование на C, C# и Java
Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
Растеризация треугольников на основе барицентрических координат C#
Мне нужен пиксельно-идеальный алгоритм заполнения треугольника, чтобы избежать сглаживания артефактов
5 ответов
💡 Видео

Друзья

Растеризация треугольника. Алгоритм заливки (заполнения)

Одним из важнейших алгоритмов растеризации является алгоритм растеризации треугольника (заполнения треугольника), т.к. в большинстве моделей построения трехмерных объектов последние состоят именно из треугольников.

Прим. В некоторых статьях этот алгоритм называется алгоритм рисования треугольника.

Схематично алгоритм можно описать следующим образом:

Треугольник разбивается на две части вертикальной линией, проходящей через среднюю точку:

Каждый из двух полученных треугольников растеризуется по отдельности.
В процессе растеризации обе стороны растеризуются параллельно, таким образом, чтобы координаты по оси y текущих точек на обоих отрезках совпадали. При этом связность растеризуемых линий (сторон треугольника) не обеспечивается:

При получении координат текущих точек горизонтальныйотрезок между ними заполняется.

При растеризации отрезков сторон используется один из алгоритмов рассмотренных ранее. Т.к. связность отрезков не обеспечивается в силу того, что единичное приращение всегда идет по оси y , будем использовать алгоритм DDA-линии с фиксированной точкой.

Приведем код алгоритма и дадим некоторые комментарии по его работе.

В функцию растеризации передаются три вершины треугольника и дескриптор контекста устройства * .

#include #include «math.h» #include «fixed.h» #define roundf(x) floor(x + 0.5f ) inline void swap( int &a, int &b) < int t; t = a; a = b; b = t; >
void triangle(HDC hdc, int x1, int y1, int x2, int y2, int x3, int y3) <
// Упорядочиваем точки p 1( x 1, y 1), // p2(x2, y2), p3(x3, y3) if (y2 swap(y1, y2); swap ( x 1, x 2); > // точки p 1, p 2 упорядочены if (y3 swap(y1, y3); swap ( x 1, x 3); > // точки p 1, p 3 упорядочены // теперь p 1 самая верхняя // осталось упорядочить p 2 и p 3 if (y2 > y3) < swap(y2, y3); swap ( x 2, x 3); >
// приращения по оси x для трёх сторон // треугольника fixed dx 13 = 0, dx 12 = 0, dx 23 = 0; // вычисляем приращения // в случае, если ординаты двух точек // совпадают, приращения // полагаются равными нулю if ( y 3 != y 1) < dx13 = int_to_fixed(x3 — x1); dx13 /= y3 — y1; > else < dx13 = 0; > if (y2 != y1) < dx12 = int_to_fixed(x2 — x1); dx12 /= (y2 — y1); > else < dx12 = 0; > if (y3 != y2) < dx23 = int_to_fixed(x3 — x2); dx23 /= (y3 — y2); > else < dx23 = 0; >	Вычисляем приращения по оси x для трёх сторон треугольника. Если ординаты двух точек совпадают (отсутствует верхний, нижний или оба полутреугольника), приращения полагаются равными нулю ** .
// «рабочие точки» // изначально они находятся в верхней точке fixed wx1 = int_to_fixed(x1); fixed wx 2 = wx 1;
// сохраняем приращение dx 13 в другой переменной int _ dx 13 = dx 13; // упорядочиваем приращения таким образом, чтобы // в процессе работы алгоритмы // точка wx 1 была всегда левее wx 2 if ( dx 13 > dx 12) < swap ( dx 13, dx 12); >	Упорядочиваем приращения таким образом, чтобы в процессе работы алгоритмы точка wx1 была всегда левее wx2 . При этом приращение dx13 может быть потеряно, оно заранее сохраняется в переменной _ dx13 .
// растеризуем верхний полутреугольник for ( int i = y 1; i y 2; i ++) < // рисуем горизонтальную линию между рабочими // точками for ( int j = fixed_to_int(wx1); j j++) < SetPixel(hdc, j, i, 0); > wx1 += dx13; wx 2 += dx 12; > Важно! Обратите внимание на граничные условия цикла. Средняя точка с ординатой y2 здесь не рисуется. При у1 = y2 (отсутствует верхний полутреугольник) на этом шаге ничего выведено не будет.
// вырожденный случай, когда верхнего полутреугольника нет // надо разнести рабочие точки по оси x, т.к. изначально они совпадают if ( y 1 == y 2) < wx1 = int_to_fixed(x1); wx2 = int_to_fixed(x2); >
// упорядочиваем приращения // (используем сохраненное приращение) if (_dx13 < swap(_dx13, dx23); >	Упорядочиваем приращения таким образом, чтобы в процессе работы алгоритмы точка wx1 была всегда левее wx2 . При этом используется сохраненное приращение _dx13 .
// растеризуем нижний полутреугольник for ( int i = y2; i // рисуем горизонтальную линию между рабочими // точками for ( int j = fixed_to_int(wx1); j SetPixel(hdc, j, i, 0); > wx1 += _dx13; wx2 += dx23; > >

Прим. * В следующей статье будет рассказано, как выводить изображение в память.
** Если внимательно проанализировать алгоритм, становится видно, что в вырожденных случаях, при y 1 = y 2 , y 2 = y 3 или y 1 = y 3 на соответствующих шагах алгоритма приращения dx 12, dx 23 или dx 13 использованы не будут. Поэтому их можно не приравнивать нулю в этих случаях :

if (y3 != y1) <
dx13 = int_to_fixed(x3 — x1);
dx13 /= y3 — y1;
>
~~else~~

Прим. Приведенная реализация может быть улучшена при помощи использования различных ухищрений, ассемблерных вставок и т.д. Настоящая статья ставит своей целью раскрыть принципиальное содержание алгоритма, сохраняя в коде разумное соотношение между простотой понимания и эффективностью работы.

Слабым местом в приведенной реализации является вывод пикселей на экран. Использование функции SetPixel в данном случае крайне неразумно. Вывод в память на порядок увеличит скорость работы приложения и избавит от необходимости реализовывать двойную буферизацию через теневой контекст устройства.

Скачать исходные тексты демонстрационных программ (в программе, при нажатии на любую клавишу, можно посмотреть, как отрисует тот же треугольник стандартная WinAPI функция)

Видео:Графика с нуля | Растеризация треугольника, интерполяцияСкачать

Программирование на C, C# и Java

Видео:РАСТЕРИЗАЦИЯ ПРЯМОЙ | БРЕЗЕНХЕМ | DDA (C++ / OpenGL)Скачать

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Видео:Графика с нуля | Точки и линии. Алгоритм БрезенхэмаСкачать

Растеризация треугольников на основе барицентрических координат C#

В этой статье мы рассмотрим алгоритм и пример программы, растеризующей треугольники с интерполяцией атрибутов вершин на основе барицентрических координат. Звучит громоздко? Не пугайтесь, все не настолько сложно.

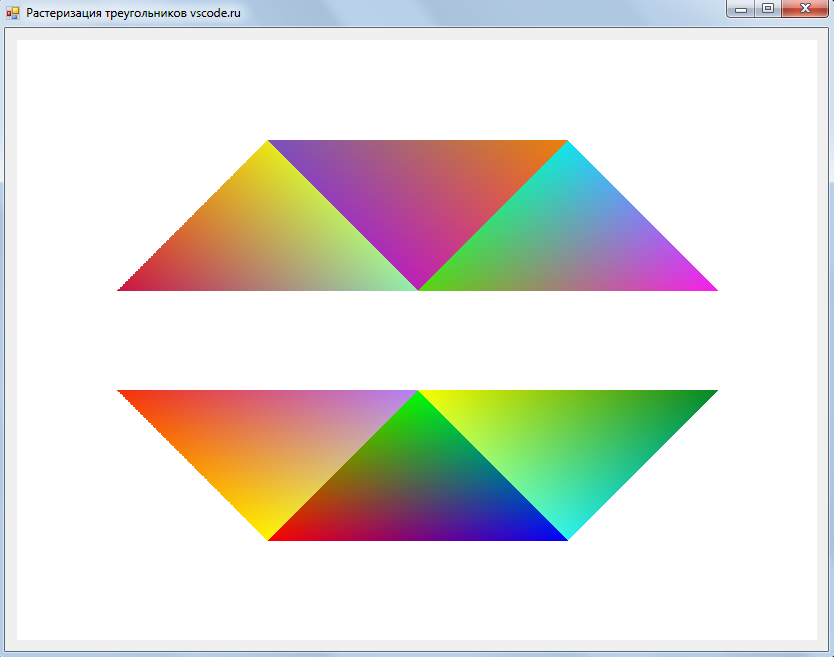
В результате разработки, мы получим программу, которая будет рисовать на экране вот такое изображение:

Итак, обо всем по порядку.

Допустим у нас имеется шесть треугольников. Даны их координаты и заданы атрибуты их вершин (цвета в вершинах). Необходимо растеризовать с интерполяцией атрибутов вершин (или проще – раскрасить, зная цвета вершин) эти треугольники. Получим своеобразный градиент.

Примечание. Интерполяция – это получение промежуточных значений величины, на основе набора известных значений.

Допустим, у нас имеется pictureBox размером 800 x 600 пикселей. За начало координат примем левый верхний угол.

В цикле for будем перемещаться по координатной плоскости (по пикселям) построчно – слева направо. Наша задача состоит в том, что бы определить, принадлежат ли координаты текущего пикселя какому-либо из треугольников. Для решения этой задачи нам потребуется использовать барицентрические координаты. Вот их формулы:

где x1, y1, x2, y2, x3, y3 – координаты вершин треугольника, а x, y – координаты текущей точки. Текущая точка принадлежит треугольнику, если выполняется условие:

(то есть все три барицентрические координаты должны принадлежать отрезку [0, 1])

Подробнее прочитать про барицентрические координаты можно здесь и здесь.

В итоге имеем такой алгоритм растеризации треугольника:

1) Значению цвета текущей точки присваивается цвет фона.

2) Вычисляются барицентрические координаты текущей точки относительно вершин текущего треугольника.

3) Выполняется проверка условия принадлежности точки треугольнику.

4) Если условие верно, то точка принадлежит треугольнику, и значению ее цвета присваивается цвет, полученный при интерполяции атрибутов вершин этого треугольника. Иначе: переходим к следующему треугольнику (если такой [еще] имеется) и пункту 2.

5) Вывод текущей точки, переход к следующей и пункту 1.

Итак, создадим в Visual Studio проект Windows Forms (С#). Поместим в форму элемент управления pictureBox и зададим в свойствах его размеры 800 x 600:

Видео:Лекция 11. Растеризация: OpenGL, Larrabee, cudarasterСкачать

Мне нужен пиксельно-идеальный алгоритм заполнения треугольника, чтобы избежать сглаживания артефактов

Я помогаю кому-то с кодом пользовательского интерфейса визуализировать математический анализ изображений. Во время этого процесса мы будем сегментировать часть 2D-фигуры на треугольники и заполнять некоторые из этих треугольников в пользовательском интерфейсе.

мы ищем алгоритм заливки, который гарантирует, что если два треугольника имеют общее ребро (в частности, если любые две вершины треугольников идентичны), то независимо от порядка рисования и сглаживания не будет пустых, развернутых пикселей на линия между ними. (Это нормально, если некоторые пиксели рисуются дважды.) Результат должен выглядеть нормально при произвольном масштабировании. Некоторые треугольники могут быть очень тонкими щепками в местах, до 1 пикселя в ширину.

В идеале это также должен быть разумно эффективный алгоритм заполнения!

сглаживание не будет использоваться в рендеринге треугольника, так как конечное изображение должно быть 1-битной глубины.

контекст является приложением распознавания изображений, поэтому все координаты вершин будут с точностью до одного пикселя.

Видео:Растеризация, ее правила и настройкаСкачать

5 ответов

учитывая требования, похоже, что есть простое решение.

во-первых, растеризация треугольников. Вы можете использовать алгоритм рисования линии Bresenham для этого (как в коде ниже) или что-нибудь, что работает. Затем заполните область между ними. Это будет работать со сколь угодно тонкими треугольниками.

чтобы убедиться, что нет пробелов независимо от порядка, в котором рисуются треугольники, и независимо от порядка вершин, поставляемых в треугольник-код рисования вы хотите растеризировать общие ребра таким же образом в треугольниках, разделяющих ребро. одинаково означает одни и те же пиксели каждый раз.

чтобы гарантировать, что каждый раз, когда вы получаете одни и те же пиксели из одних и тех же пар координат вершин, вы в основном хотите установить фиксированный порядок, то есть установить правило, которое всегда будет выбирать одну и ту же вершину из двух заданных независимо от порядка, в котором они заданы.

один простой способ применения этого порядка-рассматривать вашу линию (край треугольника) как 2-d вектор и переворачивать ее направление, если она указывает в направлении отрицательных y или параллельна оси x и указывает в направлении отрицательных X. Время для некоторых ASCII искусства! 🙂

см., здесь сегмент линии, скажем, 1 и сегмент линии 5-это действительно одна и та же вещь, единственное отличие-направление от конечной точки в начале координат до другой конечной точки. Поэтому мы сокращаем эти случаи вдвое, поворачивая сегменты с 4 по 7 в сегменты с 0 по 3 и избавиться от неоднозначности направления. IOW, мы выбираем идти в направлении увеличения y или, если y одинаковы на краю, в направлении увеличения X.

вот как вы могли бы сделать это в коде:

«+» — пиксели треугольника 1
«-» — пиксели треугольника 2
«* » — пиксели общего края между треугольниками 1 и 2

остерегайтесь, что даже если не будет незаполненных пробелов (пикселей), треугольник, пиксели которого (на общем краю) перезаписываются (из-за другого треугольника, нарисованного поверх него), может отображаться как непересекающийся или неуклюже сформированный, если он слишком тонкий. Пример:

ваше беспокойство о соседних треугольниках является действительным. Если два треугольника имеют общее ребро, вы хотите быть уверены, что каждый пиксель вдоль этого ребра «принадлежит» исключительно одному треугольнику или другому. Если один из этих пикселей не принадлежит ни одному из треугольников, у вас есть пробел. Если он принадлежит обоим треугольникам, у вас есть overdraw (что неэффективно), и цвет может зависеть от порядка отображения треугольников (который не может быть детерминированным).

так как вы не используете сглаживание, это на самом деле не слишком сложно. Это не столько умный алгоритм, который вам нужен, сколько тщательная реализация.

типичный способ растеризации треугольника-вычислить горизонтальные сегменты, которые являются частью треугольника сверху вниз. Вы делаете это, отслеживая текущий левый и правый края и, по существу, делая расчет X-перехвата для каждого края на каждой линии развертки. Это также можно сделать с помощью двух алгоритмов рисования линий в стиле Bresenhem вместе. Фактически растеризация сводится к нескольким вызовам функции, которая рисует сегмент горизонтальной линии на некотором scanline y из какой-то левой координаты x0 к некоторой правой координате x1 .

обычно это делается для того, чтобы убедиться, что растризатор округляет x-перехваты согласованным образом, так что X-координаты вычисляются последовательно независимо от того, являются ли они частью правого края одного треугольника или левого края соседний треугольник. Это гарантирует, что каждый пиксель вдоль общего края будет принадлежать и треугольников.

мы разрешаем двойное владение, настраивая DrawHLine так что он заполняет пиксели из x0 включительно до x1 эксклюзивные. Таким образом, все эти дважды принадлежащие пиксели на общем краю определяются как принадлежащие треугольнику справа от общего края.