Abcd трапеция ab cd o центр окружности

Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.

$$ 4.^$$. Диагонали трапеции разбивают её на четыре треугольника с общей вершиной (рис. 20). Площади треугольников, прилежащих к боковым сторонам, равны, а треугольники прилежащие к основаниям — подобны.

$$ 4.^$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).

$$ 4.^$$. В равнобокой трапеции углы при основании равны (рис. 22).

$$ 4.^$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).

$$ 4.^$$. В равнобокой трапеции диагонали равны (рис. 24).

$$ 4.^$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме

(рис. 25, основания равны `a` и `b`, `a>b`).

$$ 4.^$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).

$$ 4.^$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).

$$ 4.^$$.В равнобокой трапеции `d^2=c^2+ab`, где `d` — диагональ, `c` — боковая сторона, `a` и `b` основания.

Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.

$$ 4.^$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).

$$ 4.^$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

Докажем, например, утверждение $$ 4.^$$ .

Применяем теорему косинусов (см. рис. 29а и б):

`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,

`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).

Проводим `CK«||«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:

В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем

Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.

`AC=6`, `BM=MC`, `AN=ND`, `MN=5` (рис. 30а). Во всякой трапеции середины оснований и точка пересечения диагоналей лежат на од-ной прямой (свойство $$ 4.^$$). Треугольник `BOC` прямоугольный (по условию `AC_|_BD`), `OM` — его медиана, проведённая из вершины прямого угла, она равна половине гипотенузы: `OM=1/2BC`. Аналогично устанавливается `ON=1/2AD`, поэтому `MN=1/2(BC+AD)`. Через точку `D` проведём прямую, параллельную диагонали `AC`, пусть `K` — её точка пересечения с прямой `BC` (рис. 30б).

По построению `ACKD` — параллелограмм, `DK=AC`, `CK=AD` и `/_BDK=90^@`

(т. к. угол `BDK` — это угол между диагоналями трапеции).

Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то

Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.

Пусть `BC=a`, `AD=b`, и пусть `h` — высота трапеции (рис. 31). По свойству $$ 4.^$$ `S_(ABO)=S_(CDO)`, обозначим эту площадь `S_0` (действительно, `S_(ABD)=S_(ACD)`, т. к. у них общие основания и равные высоты, т. е. `S_(AOB)+S_(AOD)=S_(COD)+S_(AOD)`, откуда следует `S_(AOB)=S_(COD)`). Так как `S_(ABC)=S_0 + S_1=1/2ah` и `S_(ACD)=S_0+S_2=1/2bh`, то `(S_0+S_1)/(S_0 + S_2)=a/b`.

Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна

Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).

Найти радиус окружности, описанной около этой трапеции.

Трапеция равнобокая, по свойству $$ 4.^$$ около этой трапеции можно описать окружность. Пусть `BK_|_AD`, по свойству $$ 4.^$$

Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда

$$ 4.^$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.

$$ 4.^$$. Если `S_1` и `S_2` — площади треугольников, прилежащих к основаниям, то площади треугольников, прилежащих к боковым сторонам равны `sqrt(S_1S_2)`, а площадь всей трапеции равна `(sqrt(S_1) +sqrt(S_2))^2`.

$$ 4.^$$. Радиус окружности, описанной около трапеции, находится по формуле `R+a/(2sin alpha)`, где `a` — какая-то сторона (или диагональ трапеции), `alpha` — смотрящий на неё вписанный угол.

Видео:Где центр окружности? ТрапецияСкачать

Решение задач по теме «Перпендикуляр и наклонные»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Решение задач по теме «Перпендикуляр и наклонные» Задачи на готовых чертежах

Дано: АВ- перпендикуляр, АС и AD-наклонные, АСВ=30°, АС=16, ВD=6 Найти: АD 1 Ответ: 10 А В D C 30° 16 6

Дано: АВ- перпендикуляр, АС и AD-наклонные, АСВ=45°, АС= , ВD=6 Найти: АD 2 Ответ: 10 А В D C 45° 6

Дано: АВ- перпендикуляр, АС и AD-наклонные, АСВ=60°, АС= 4, ВD= Найти: АD 4 3 Ответ: 5 А В D C 60°

Решение задач по теме «Перпендикуляр и наклонные» Задачи на готовых чертежах

Дано: АВ- перпендикуляр к плоскости , АС и AD-наклонные, АСВ= 30°, АDB= 60°, СВD= 90°, АВ=1 Найти: РCAD 4 Ответ: 1 А В C D 60° 30°

Дано: АВ- перпендикуляр к плоскости , АС и AD-наклонные, АСВ= АDB= 30°, САD= 60°, RACD= Найти: AB 60° 5 Ответ: 1,5 А В C D 30° 30°

Дано: ABCD-трапеция, О- центр окружности, описанной вокруг трапеции, ОЕ (АВС), АЕ=10, ОЕ=8, ВАD=30° Найти: BD. О 6 6 Ответ: А В С D E 8 10 30°

Дано: АВС, О- центр вписанной окружности, OD (ABC), АС=ВС=5, АВ=6, DO=1, АМ=МВ Найти: DM. 1 7 Ответ: А В С D О М 6 5

С Дано: АВС, АСВ=90°, О — центр описанной окружности, АМ=МС, OD (АВС), АВ=5, АС=3, DO= Найти: МD. 4 8 Ответ: А В D О М 3 5

Дано: АВС, ABС=90°, О- центр вписанной окружности, OD (ABC), АВ=3, ВС=4, DO= , ОМ=r Найти: DM. 2 9 Ответ: А В С D О М 3 4

D Дано: АВС, ACB=90°, О- центр вписанной окружности, OD (ABC), АС=6, ВС=8, DO= , ОМ=r Найти: 12 10 Ответ: А В С О М 6 8

Дано: АВСD-трапеция, описанная вокруг окружности с центром О, АВ=СD, ОЕ (АВС), РАВСD=16, СDА=30°, ОЕ=4, М и К-точки касания окружности со сторонами ВС и АD Найти: ЕК 4 Ответ: Р 11 А В С D О 30° К М Е

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 943 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 679 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 306 человек из 67 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 503 233 материала в базе

Материал подходит для УМК

«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

Другие материалы

• 31.05.2018
• 3452
• 409

• 31.05.2018
• 779
• 1

• 31.05.2018
• 1045
• 1

• 31.05.2018
• 10381
• 118

• 31.05.2018
• 20394
• 178

• 31.05.2018
• 3903
• 13

• 31.05.2018
• 1388
• 20

• 31.05.2018
• 1200
• 8

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 31.05.2018 10806
• PPTX 346.9 кбайт
• 61 скачивание
• Оцените материал:

Настоящий материал опубликован пользователем Щенников Алексей Сергеевич. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 3 месяца
• Подписчики: 2
• Всего просмотров: 464042
• Всего материалов: 115

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Геометрия Точка O центр окружности вписанной в треугольник ABC BC = a AC = b угол AOB = 120 НайдитеСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Онлайн-семинар о снятии эмоционального напряжения у детей и подростков

Время чтения: 2 минуты

УрФУ возглавил рейтинг медиаактивности вузов

Время чтения: 1 минута

Большинство российских вузов используют смешанный формат обучения

Время чтения: 1 минута

Большинство российских школьников недовольны качеством питания в столовых

Время чтения: 1 минута

В Петербурге введут новые COVID-ограничения для несовершеннолетних

Время чтения: 2 минуты

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:ЕГЭ 2022 16 вариант 3 задача.Скачать

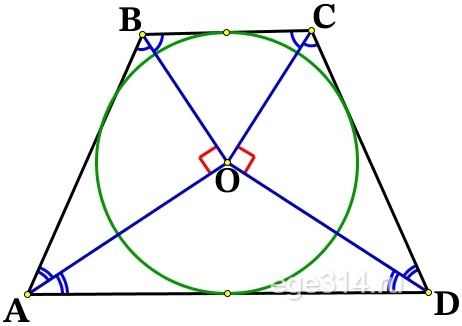
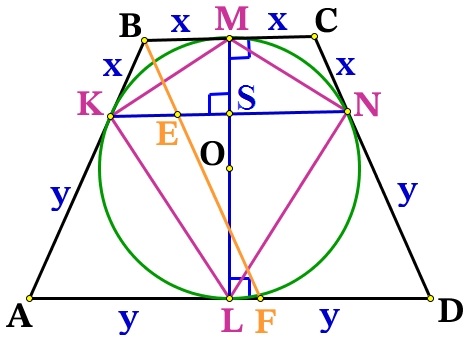
Решение №2583 Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.

Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.

а) Докажите, что треугольник АОВ прямоугольный.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет frac площади трапеции ABCD.

Источник: Ященко ЕГЭ 2022 (36 вар)

а) Доказать , что в ΔАОВ ∠АОВ = 90° (тогда он прямоугольный) .

Окружность вписана в углы: ∠ВAD, ∠ADC, ∠DCB и ∠CBA. Центр окружности, которая вписана в угол, расположен на биссектрисе этого угла, значит АО, DO, СО, ВО – биссектрисы и делят соответствующие углы пополам.

∠ВAD + ∠CBA = 180°
∠ADC + ∠DCB = 180°

Как односторонние углы, при параллельных прямых AD||ВС (основания трапеции) и секущих AB и СD соответственно.
Зная о биссектрисах поделим всё на 2:

Рассмотрим треугольники ΔАВО и ΔDCO, сумма углов любого треугольника равна 180°, тогда:

∠AOB = ∠COD = 90°

Что и требовалось доказать.

б) Найти: frac , если АВ = СD, S_=fraccdot S_ :

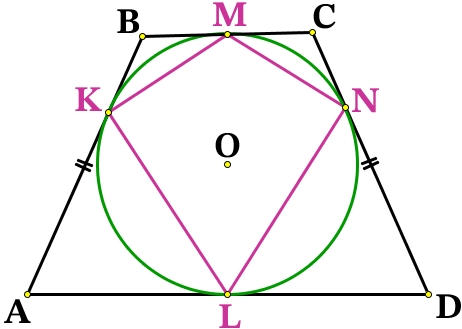
Отрезки касательных к окружности, проведённые из одной точки, равны:

BM = BK
CM = CN
AK = AL
DL = DN

Т.к. AB = CD, то:

BK = СN = BM = CM = x
AK = DN = AL = DL = y

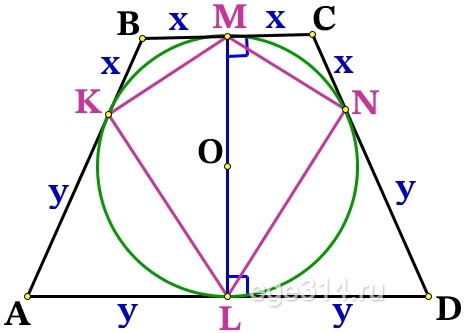
Проведём радиусы из точки О к касательным ВС и AD, тогда ОМ⊥ВС, OL⊥AD, точка О∈OM, O∈OL, значит МL это одна прямая и высота трапеции:

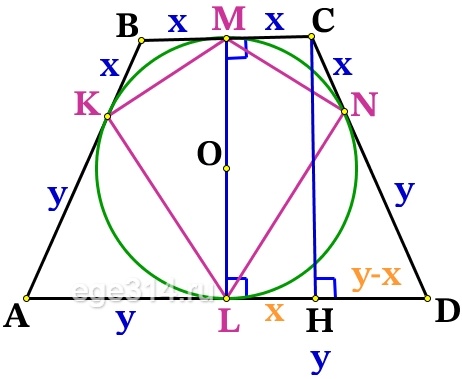
Проведём ещё одну высоту трапеции СН:

MC = LH, МCHL – прямоугольник, значит MC = LH = x , найдём HD:

HD = LD – LH = y – x

Из прямоугольного ΔСHD по теореме Пифагора найдём СН:

СН 2 + HD 2 = CD 2
CH 2 + (y – x) 2 = (y + x) 2
CH 2 = (y + x) 2 – (y – x) 2 = y 2 + 2xy + x 2 – y 2 + 2xy – x 2 = 4xy
CH=sqrt=2sqrt

Выразим площадь S_{ABCD :}

В четырёхугольнике проведём KMNL диагональ KN, прямые ВС и KN отсекают равные отрезки ВК = СN = x, значит они по теорема Фалеса параллельны ВС||KN, т.к. BC⊥LM, то KM⊥ML, значит угол между диагоналями ∠MSK = 90°.
Диагональ ML = 2sqrt , как высота трапеции.
Проведём BF||CD и пересекающая KN в точке Е. BCDF – параллелограмм, значит EN = BC = 2x.

ΔАВF подобен ΔВКЕ (∠В – общий, ∠ВКЕ = ∠ВАF – соответственные). Из пропорциональности сторон найдём КЕ:

Найдём диагональ KN:

Выразим площадь S_KMNL :

S_=fraccdot MLcdot KNcdot sin angle MSK=fraccdot 2sqrtcdot fraccdot sin 90^=sqrtcdot fraccdot 1= frac<4xysqrt>

Подставим выраженные площади с исходное отношение:

Т.к. у нас у большее основание, а х меньшее, то их отношение равно 8.

📹 Видео

ОГЭ без рекламы математика 17 вариант задача 25Скачать

[ОГЭ] Найдите боковую сторону АВ трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120Скачать

В трапеции ABCD AB=CD, ∠BDA=35° ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

ЕГЭ Задание 16 Трапеция и две окружностиСкачать

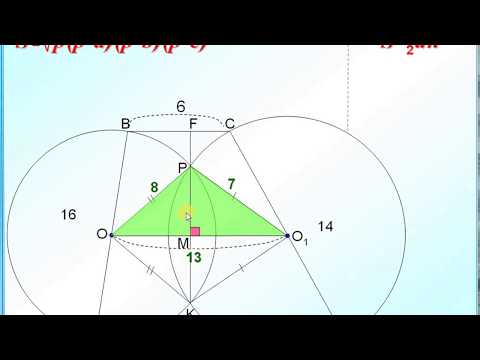
🔴 В трапеции ABCD известно, что AB=CD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

В четырехугольник ABCD вписана окружность, AB = 10, BC = 11 и CD = 15. Найдите четвертую сторону.Скачать

2020 точка О центр окружности на которой лежат точки A B и C известно что Угол ABC равен 62 градусаСкачать

№552. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите:Скачать

Геометрия В треугольнике ABC известны длины сторон AB = 18, AC = 36, точка O — центр окружностиСкачать

2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать

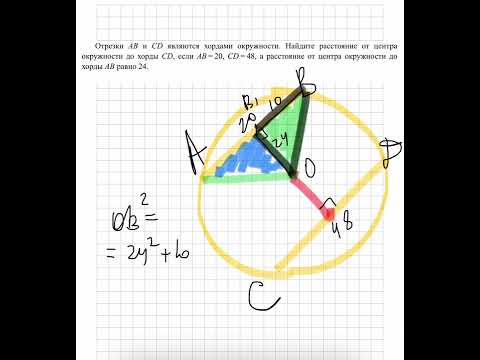
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CDСкачать

№346. Точки М и N — середины оснований АВ и CD трапеции ABCD, а О — произвольнаяСкачать

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. окружность проходит через точки C,DСкачать