Зависимость между сторонами многоугольников и радиусом окружности

Для того, чтобы научиться решать задачи из задания В6 на нахождение радиуса окружности, вписанной в правильный многоугольник, или описанной около него, не нужно запоминать большое количество формул. Нужно только вспомнить, как соотносятся стороны и углы в прямоугольном треугольнике.

И применить эти знания в немного другой ситуации.

Окружность называется описанной около многоугольника, если она проходит через все его вершины. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров, проведенных к сторонам многоугольника.

Окружность называется вписанной в многоугольник, если она касается всех сторон многоугольника. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.

В правильном многоугольнике центр вписанной и описанной окружности совпадают.

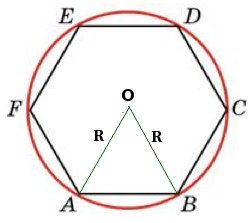
Посмотрим, как соотносятся между собой радиусы вписанной и описанной окружности и сторона правильного многоугольника. Рассмотрим фрагмент правильного многоугольника:

Здесь

АВ — сторона правильного треугольника

ОК — радиус вписанной окружности

ОВ, ОА — радиусы описанной окружности

Очевидно, что треугольник АОВ — равнобедренный, поэтому ОК является высотой, биссектрисой и медианой.

Рассмотрим треугольник ОКВ. С его помощью мы найдем, как соотносятся между собой сторона правильного многоугольника, радиус вписанной и описанной окружности.

Угол AOB= , где n- количество сторон многоугольника. Тогда угол — то есть его величину мы знаем всегда.

радиус вписанной окружности r — является прилежащим катетом прямоугольного треугольника ОКВ

половина стороны многоугольника а/2 является противолежащим катетом прямоугольного треугольника ОКВ

радиус описанной окружности R является гипотенузой прямоугольного треугольника ОКВ

Решим несколько задач из Открытого банка заданий для подготовки к ЕГЭ по математике:

1 . Задание B7 (№ 27944)

Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.

Проведем радиусы вписанной и описанной окружности и рассмотрим наш «волшебный» прямоугольный треугольник:

По условию , надо найти

Тогда

Ответ: 4

2 . Задание B7 (№ 27929)

Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.

В этой задаче мы пойдем немного другим путем, и рассмотрим треугольник АОВ:

Угол АОВ=

Найдем сторону шестиугольника. Так как все стороны правильного шестиугольника равны, . Отсюда

Треугольник АОВ равнобедренный с углом , а, значит, равносторонний. Следовательно, и

Ответ: 24.

Запомните : в правильном шестиугольнике сторона равна радиусу описанной окружности.

3 . Задание B7 (№ 27917)

Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .

Рассмотрим треугольник ВОК:

Ответ: 1,5

4. Задание B7 (№ 27909)

Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.

Рассмотрим треугольник ВОК:

Ответ: 0,5

Купить видеокурс «ВСЯ ГЕОМЕТРИЯ. Часть В»

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

1. ) Зависимость между стороной правильного многоугольника и радиусом описанной и вписанной окружности (вывод формулы)?

Геометрия | 5 — 9 классы

1. ) Зависимость между стороной правильного многоугольника и радиусом описанной и вписанной окружности (вывод формулы).

Установление этой зависимости для квадрата, правильного треугольника, шестиугольника.

2. ) Задача по теме «Подобие треугольников» : а) одна из сторон треугольника равна 8, а два из его углов равны соответственно 30° и 45°.

Найдите все возможные значения периметра треугольника ; б) один из углов треугольника 150°, а две из его сторон равны 2 и 7.

Найдите все возможные значения площади треугольника.

R = a : (2 * tg45) = a / 2 — дляквадрата

r = a : (2 * tg60) = a ; (2√3) — длятреугольника

r = a : (2 * tg30) = a * √3 : (2) — дляшестиугольника.

Видео:Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

Сторона правильного треугольника равна корню из 3?

Сторона правильного треугольника равна корню из 3.

Найдите радиус окружности, вписанной в этот треугольник.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Сторона правильного шестиугольника равна 2 см?

Сторона правильного шестиугольника равна 2 см.

Найдите сторону правильного треугольника, вписанного в окружность.

Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Найдите сторону правильного треугольника вписанного в окружность если сторона правильного шестиугольника описанного около этой окружности равна 2 см?

Найдите сторону правильного треугольника вписанного в окружность если сторона правильного шестиугольника описанного около этой окружности равна 2 см.

Видео:112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Сторона правильного шестиугольника, описанного около окружности, равна 2 см?

Сторона правильного шестиугольника, описанного около окружности, равна 2 см.

Найдите сторону правильного треугольника, вписанного в эту окружность.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Зависимость между стороной правильного многоугольника и радиусом описанной и вписанной окружности?

Зависимость между стороной правильного многоугольника и радиусом описанной и вписанной окружности.

) Установление этой зависимости для квадрата, правильного треугольника, шестиугольника.

Видео:Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Сторона правильного вписанного в окружность треугольника равна а?

Сторона правильного вписанного в окружность треугольника равна а.

Найдите сторону квадрата, вписанного в эту окружность.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Задача : Сторона правильного шестиугольника, описанного около окружности, равна 2 см?

Задача : Сторона правильного шестиугольника, описанного около окружности, равна 2 см.

Найдите сторону правильного треугольника, вписанного в окуржность.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Один из углов треугольника 150, а две из его сторон равны 2 и 7?

Один из углов треугольника 150, а две из его сторон равны 2 и 7.

Найдите все возможные значения площади треугольника.

Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

1. Сторона правильного треугольника равна 4корня из 3?

1. Сторона правильного треугольника равна 4корня из 3.

Найдите радиус окружности ю, вписанной в этот треугольник 2.

Радиус окружности, вписанной в правильный треугольник равен корень из 3 / 2.

Найдите сторону этого треугольника.

Видео:Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

Сторона правильного треугольника равна 8корням из 3?

Сторона правильного треугольника равна 8корням из 3.

Найдите радиус окружности вписанной в этот треугольник.

Вопрос 1. ) Зависимость между стороной правильного многоугольника и радиусом описанной и вписанной окружности (вывод формулы)?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

По теореме Пифагора АB ^ 2 — (AC / 2) ^ 2 = AH ^ 2 100 — 64 = 36 = 6 * 6 = AH ^ 2 AH = 6.

Начерти угол A B C что бы AC пересикались так же как BC AC относиться к AB BC относится AB.

Окружность проходит через точку А = > СА — радиус r = CA = ✓(( — 1 — 2)² + ( — 2 — ( — 3))²) = = ✓(9 + 1) = ✓10 Уравнение окружности получается : (х — 2)² + (у — ( — 3))² = (✓10)² (х — 2)² + (у + 3)² = 10.

Ну ок 2, 8 первый и 12, 8 второй.

Пожалуйста вот ничего сложного.

Сечение конуса по образующим — равносторонний треугольник, так как угол при основании равен 60°. Тогда высота конуса по формуле h = a * √3 / 2 получим h = 4, 5√3см. Второй вариант : Высота конуса — это катет прямоугольного треугольника, лежащий про..

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Зависимость между сторонами многоугольников и радиусом окружности

Ключевые слова: многоугольник, правильный многоугольник, сторона, угол, вписанная, описанная окружность

Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.

Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон.

Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.

См. также:
Вписанная окружность, Описанная окружность, Выпуклый четырёхугольник, Произвольный выпуклый многоугольник

💥 Видео

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Правильные многоугольники. Урок 11. Геометрия 9 классСкачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Геометрия 9 класс (Урок№26 - Построение правильных многоугольников.)Скачать

110. Окружность, описанная около правильного многоугольникаСкачать

ЕГЭ. Описывающая многоугольник окружность.Скачать