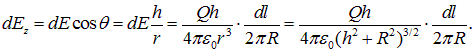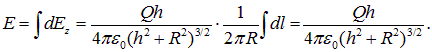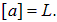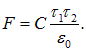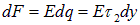Заряд равномерно распределен по окружности радиусом (3 видео)

Заряд равномерно распределен по окружности

Содержание

1.2. Закон Кулона. Принцип суперпозиции
Заряд равномерно распределен по окружности
Заряд q = 10 нКл равномерно распределён по дуге окружности, радиус которой R = 1,0 см, а угол раствора = 2/3. Используя принцип суперпозиции, определите напряжённость электростатического поля
Описание и исходные данные задания, 50% решения + фотография:
Заряд q = 10 нКл равномерно распределён по дуге окружности, радиус которой R = 1,0 см, а угол раствора = 2/3. Используя принцип суперпозиции, определите напряжённость электростатического поля
Описание и исходные данные задания, 50% решения + фотография:
Заряд q равномерно распределен по тонкому кольцу радиусом R.
📽️ Видео

Видео:Урок 224. Напряженность поля неточечных зарядовСкачать

1.2. Закон Кулона. Принцип суперпозиции

Пусть имеются два заряженных макроскопических тела, размеры которых пренебрежимо малы по сравнению с расстоянием между ними. В этом случае каждое тело можно считать материальной точкой или «точечным зарядом».

Французский физик Ш. Кулон (1736–1806) экспериментально установил закон, носящий его имя (закон Кулона) (рис. 1.5):

Рис. 1.5. Ш. Куло́н (1736–1806) — французский инженер и физик

В вакууме сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов, обратно пропорциональна квадрату расстояния между ними и направлена по прямой, соединяющей эти заряды:

На рис. 1.6 показаны электрические силы отталкивания, возникающие между двумя одноименными точечными зарядами.

Рис. 1.6. Электрические силы отталкивания между двумя одноименными точечными зарядами

Напомним, что , где и — радиус-векторы первого и второго зарядов, поэтому силу, действующую на второй заряд в результате его электростатического — «кулоновского» взаимодействия с первым зарядом можно переписать в следующем «развернутом» виде

Отметим следующее, удобное при решении задач, правило: если первым индексом у силы ставить номер того заряда, на который действует эта сила, а вторым – номер того заряда, который создает эту силу, то соблюдение того же порядка индексов в правой части формулы автоматически обеспечивает правильное направление силы — соответствующее знаку произведения зарядов: — отталкивание и — притяжение, при этом коэффициент всегда.

Для измерения сил, действующих между точечными зарядами, был использован созданный Кулоном прибор, называемый крутильными весами (рис. 1.7, 1.8).

Рис. 1.7. Крутильные весы Ш. Кулона (рисунок из работы 1785 г.). Измерялась сила, действующая между заряженными шарами a и b

Рис. 1.8. Крутильные весы Ш. Кулона (точка подвеса)

На тонкой упругой нити подвешено легкое коромысло, на одном конце которого укреплен металлический шарик, а на другом — противовес. Рядом с первым шариком можно расположить другой такой же неподвижный шарик. Стеклянный цилиндр защищает чувствительные части прибора от движения воздуха.

Чтобы установить зависимость силы электростатического взаимодействия от расстояния между зарядами, шарикам сообщают произвольные заряды, прикасаясь к ним третьим заряженным шариком, укрепленным на ручке из диэлектрика. По углу закручивания упругой нити можно измерить силу отталкивания одноименно заряженных шариков, а по шкале прибора — расстояние между ними.

Надо сказать, что Кулон не был первым ученым, установившим закон взаимодействия зарядов, носящий теперь его имя: за 30 лет до него к такому же выводу пришел Б. Франклин. Более того, точность измерений Кулона уступала точности ранее проведенных экспериментов (Г. Кавендиш).

Чтобы ввести количественную меру для определения точности измерений, предположим, что на самом деле сила взаимодействия зарядов обратна не квадрату расстояния между ними, а какой-то другой степени:

Никто из ученых не возьмется утверждать, что d = 0 точно. Правильное заключение должно звучать так: эксперименты показали, что d не превышает.

Результаты некоторых из этих экспериментов приведены в таблице 1.

Таблица 1.

Результаты прямых экспериментов по проверке закона Кулона

Эксперимент

Год

Сам Шарль Кулон проверил закон обратных квадратов с точностью до нескольких процентов. В таблице приведены результаты прямых лабораторных экспериментов. Косвенные данные, основанные на наблюдениях магнитных полей в космическом пространстве, приводят к еще более сильным ограничениям на величину d. Таким образом, закон Кулона можно считать надежно установленным фактом.

В СИ единица силы тока (ампер) является основной, следовательно, единица заряда q оказывается производной. Как мы увидим в дальнейшем, сила тока I определяется как отношение заряда , протекающего через поперечное сечение проводника за время , к этому времени:

Отсюда видно, что сила постоянного тока численно равна заряду, протекающему через поперечное сечение проводника за единицу времени, соответственно этому:

В СИ единицей измерения электрического заряда является кулон (Кл) — электрический заряд, протекающий за 1 секунду через поперечное сечение проводника при постоянной силе тока в 1 A:

Коэффициент пропорциональности в законе Кулона записывается в виде:

При такой форме записи из эксперимента следует значение величины , которую принято называть электрической постоянной. Приближенное численное значение электрической постоянной следующее:

Поскольку чаще всего входит в уравнения в виде комбинации

приведём численное значение самого коэффициента

Как и в случае элементарного заряда, численное значение электрической постоянной определено экспериментально с высокой точностью:

Кулон — слишком большая единица для использования на практике. Например, два заряда в 1 Кл каждый, расположенные в вакууме на расстоянии 100 м друг от друга, отталкиваются с силой

Для сравнения: с такой силой давит на землю тело массой

Это примерно масса грузового железнодорожного вагона, например, с углем.

Принцип суперпозиции полей

Принцип суперпозиции представляет собой утверждение, согласно которому результирующий эффект сложного процесса воздействия представляет собой сумму эффектов, вызываемых каждым воздействием в отдельности, при условии, что последние взаимно не влияют друг на друга (Физический энциклопедический словарь, Москва, «Советская энциклопедия», 1983, стр. 731). Экспериментально установлено, что принцип суперпозиции справедлив для рассматриваемого здесь электромагнитного взаимодействия.

В случае взаимодействия заряженных тел принцип суперпозиции проявляет себя следующим образом: сила, с которой данная система зарядов действует на некоторый точечный заряд, равна векторной сумме сил, с которыми действует на него каждый из зарядов системы.

Поясним это на простом примере. Пусть имеются два заряженных тела, действующие на третье с силами и соответственно. Тогда система из этих двух тел — первого и второго — действует на третье тело с силой

Это правило справедливо для любых заряженных тел, не только для точечных зарядов. Силы взаимодействия двух произвольных систем точечных зарядов вычисляются в Дополнении 1 в конце этой главы.

Отсюда следует, что электрическое поле системы зарядов определяется векторной суммой напряженностей полей, создаваемых отдельными зарядами системы, т. е.

Сложение напряженностей электрических полей по правилу сложения векторов выражает так называемый принцип суперпозиции (независимого наложения) электрических полей. Физический смысл этого свойства заключается в том, что электростатическое поле создается только покоящимися зарядами. Значит, поля различных зарядов «не мешают» друг другу, и поэтому суммарное поле системы зарядов можно подсчитать как векторную сумму полей от каждого из них в отдельности.

Так как элементарный заряд весьма мал, а макроскопические тела содержат очень большое количество элементарных зарядов, то распределение зарядов по таким телам в большинстве случаев можно считать непрерывным. Для того чтобы описать как именно распределен (однородно, неоднородно, где зарядов больше, где их меньше и т. п.) заряд по телу введем плотности заряда следующих трех видов:

· объемная плотность заряда :

где dV — физически бесконечно малый элемент объема;

· поверхностная плотность заряда :

где dS — физически бесконечно малый элемент поверхности;

· линейная плотность заряда :

где — физически бесконечно малый элемент длины линии.

Здесь всюду — заряд рассматриваемого физически бесконечно малого элемента (объема, участка поверхности, отрезка линии). Под физически бесконечно малым участком тела здесь и ниже понимается такой его участок, который, с одной стороны, настолько мал, что в условиях данной задачи, его можно считать материальной точкой, а, с другой стороны, он настолько велик, что дискретностью заряда (см. соотношение ) этого участка можно пренебречь.

Общие выражения для сил взаимодействия систем непрерывно распределенных зарядов приведены в Дополнении 2 в конце главы.

Пример 1. Электрический заряд 50 нКл равномерно распределен по тонкому стержню длиной 15 см. На продолжении оси стержня на расстоянии 10 см от ближайшего его конца находится точечный заряд 100 нКл (рис. 1.9). Определить силу взаимодействия заряженного стержня и точечного заряда.

Рис. 1.9. Взаимодействие заряженного стержня с точечным зарядом

Решение. В этой задаче силу F нельзя определить, написав закон Кулона в форме или (1.3). В самом деле, чему равно расстояние между стержнем и зарядом: r, r + a/2, r + a? Поскольку по условиям задачи мы не имеем права считать, что a , когда стержень можно считать материальной точкой, выражение для силы взаимодействия заряда и стержня, как и должно быть, принимает обычную форму закона Кулона для силы взаимодействия двух точечных зарядов:

Пример 2. Кольцо радиусом несет равномерно распределенный заряд . Какова сила взаимодействия кольца с точечным зарядом q, расположенным на оси кольца на расстоянии от его центра (рис. 1.10).

Решение. По условию, заряд равномерно распределен на кольце радиусом . Разделив на длину окружности, получим линейную плотность заряда на кольце Выделим на кольце элемент длиной . Его заряд равен .

Рис. 1.10. Взаимодействия кольца с точечным зарядом

В точке q этот элемент создает электрическое поле

Нас интересует лишь продольная компонента поля, ибо при суммировании вклада от всех элементов кольца только она отлична от нуля:

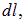
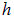
Интегрируя по находим электрическое поле на оси кольца на расстоянии от его центра:

Отсюда находим искомую силу взаимодействия кольца с зарядом q:

Обсудим полученный результат. При больших расстояниях до кольца величиной радиуса кольца под знаком радикала можно пренебречь, и мы получаем приближенное выражение

Это не удивительно, так как на больших расстояниях кольцо выглядит точечным зарядом и сила взаимодействия дается обычным законом Кулона. На малых расстояниях ситуация резко меняется. Так, при помещении пробного заряда q в центр кольца сила взаимодействия равна нулю. Это тоже не удивительно: в этом случае заряд q притягивается с равной силой всеми элементами кольца, и действие всех этих сил взаимно компенсируется.

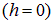
Поскольку при и при электрическое поле равно нулю, где-то при промежуточном значении электрическое поле кольца максимально. Найдем эту точку, дифференцируя выражение для напряженности Е по расстоянию

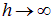
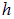
Приравнивая производную нулю, находим точку где поле максимально. Оно равно в этой точке

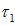
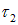
Пример 3. Две взаимно перпендикулярные бесконечно длинные нити, несущие равномерно распределенные заряды с линейными плотностями и находятся на расстоянии а друг от друга (рис. 1.11). Как зависит сила взаимодействия между нитями от расстояния а?

Решение. Сначала обсудим решение этой задачи методом анализа размерностей. Сила взаимодействия между нитями может зависеть от плотностей заряда на них, расстояния между нитями и электрической постоянной, то есть искомая формула имеет вид:

где 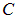— безразмерная постоянная (число). Заметим, что вследствие симметричного расположения нитей плотности заряда на них могут входить только симметричным же образом, в одинаковых степенях. Размерности входящих сюда величин в СИ известны:

Рис. 1.11. Взаимодействие двух взаимно перпендикулярных бесконечно длинных нитей

По сравнению с механикой здесь появилась новая величина — размерность 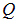электрического заряда. Объединяя две предыдущие формулы, получаем уравнение для размерностей:

Приравнивая степени при М и Т в обеих частях этого уравнения, немедленно получаем В левой части нет величины размерности заряда, откуда следует, что или Наконец, приравнивая степени при размерности длины, получаем уравнение откуда следует, что Окончательно имеем:

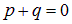
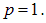
Таким образом, оказывается, что сила взаимодействия нитей не зависит от расстояния между ними. Напомним, что безразмерную постоянную С методом анализа размерностей определить невозможно. В сущности мы уже получили ответ на вопрос задачи, но приведем также и точное ее решение, которое позволит найти С. На рис. 1.11 справа показан вид сверху на плоскость, содержащую нить 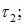точкой А отмечено сечение плоскостью чертежа нити . Напряженность электрического поля, создаваемого нитью в точке, где находится элемент второй нити, равна

На элемент нити действует сила

Нас, однако, интересует лишь компонента 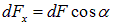этой силы вдоль оси ибо продольная составляющая компенсируется точно такой же силой, действующей на симметричный элемент нити внизу. Выразим все расстояния через угол :

Получаем в итоге выражение для составляющей силы, действующей на элемент

Видео:3.9Скачать

Заряд равномерно распределен по окружности

Положительный электрический заряд Q равномерно распределён по тонкому прямому отрезку. На продолжении этого отрезка находится точечный положительный заряд q (см. рисунок).

Куда направлена относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) сила, действующая на заряд q со стороны заряда Q? Ответ запишите словом (словами).

Разобьём отрезок с зарядом Q на маленькие отрезки положительных зарядов, которые можно считать точечными. Каждый из них отталкивает положительный заряд q вправо. Значит, суммарная сила, действующая на заряд q со стороны заряда Q, направлена вправо.

Видео:Поле заряженного кольцаСкачать

Заряд q = 10 нКл равномерно распределён по дуге окружности, радиус которой R = 1,0 см, а угол раствора = 2/3. Используя принцип суперпозиции, определите напряжённость электростатического поля

Готовое решение: Заказ №8798

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 29.09.2020

Цена: 209 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

№2 324. Заряд q = 10 нКл равномерно распределён по дуге окружности, радиус которой R = 1,0 см, а угол раствора a = 2 p /3. Используя принцип суперпозиции, определите напряжённость электростатического поля E в центре кривизны дуги.

Решение.

Угол раствора соответствует трети кольца. Треть кольца радиуса имеет длину:

Определим линейную плотность заряда, расположенного на дуге:

Если вам нужно решить физику, тогда нажмите ➔ помощь по физике.

Похожие готовые решения:

Поверхностная плотность заряда металлической сферы = 0,33 мкКл/м2. Потенциал сферы на расстоянии r = 1,5 см от поверхности равен = 750 В. Найдите радиус R сферы.
Какую работу надо совершить, чтобы увеличить расстояние между пластинами плоского вакуумного конденсатора с площадью пластин S = 100 см2 от расстояния x1 = 0,03 м до расстояния x2 = 0,10 м?
Бесконечная прямая нить, равномерно заряженная с линейной плотностью заряда 1 = +3,0•10-7 Кл/м, и отрезок нити длиной l = 20 см, равномерно заряженный с линейной плотностью заряда 2 = +2,0•1
Треть тонкого кольца радиуса R = 10 см несёт распределённый заряд Q = 50 нКл. Определить напряжённость E электрического поля, создаваемого распределённым зарядом в точке O, совпадающей с центром

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Заряд q = 10 нКл равномерно распределён по дуге окружности, радиус которой R = 1,0 см, а угол раствора = 2/3. Используя принцип суперпозиции, определите напряжённость электростатического поля

Готовое решение: Заказ №8798

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 29.09.2020

Цена: 209 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Описание и исходные данные задания, 50% решения + фотография:

Решение.

Угол раствора соответствует трети кольца. Треть кольца радиуса имеет длину:

Определим линейную плотность заряда, расположенного на дуге:

Если вам нужно решить физику, тогда нажмите ➔ помощь по физике.

Похожие готовые решения:

Поверхностная плотность заряда металлической сферы = 0,33 мкКл/м2. Потенциал сферы на расстоянии r = 1,5 см от поверхности равен = 750 В. Найдите радиус R сферы.
Какую работу надо совершить, чтобы увеличить расстояние между пластинами плоского вакуумного конденсатора с площадью пластин S = 100 см2 от расстояния x1 = 0,03 м до расстояния x2 = 0,10 м?
Бесконечная прямая нить, равномерно заряженная с линейной плотностью заряда 1 = +3,0•10-7 Кл/м, и отрезок нити длиной l = 20 см, равномерно заряженный с линейной плотностью заряда 2 = +2,0•1
Треть тонкого кольца радиуса R = 10 см несёт распределённый заряд Q = 50 нКл. Определить напряжённость E электрического поля, создаваемого распределённым зарядом в точке O, совпадающей с центром

Присылайте задания в любое время дня и ночи в ➔

Видео:Физика - движение по окружностиСкачать

Заряд q равномерно распределен по тонкому кольцу радиусом R.

🎓 Заказ №: 21949

⟾ Тип работы: Задача

📕 Предмет: Физика

✅ Статус: Выполнен (Проверен преподавателем)

🔥 Цена: 149 руб.

👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.

➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.

➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.

⚡ Условие + 37% решения:

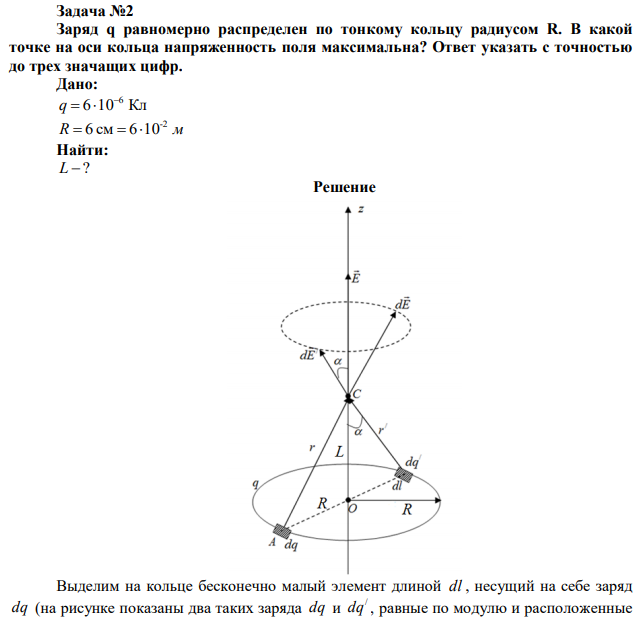
Заряд q равномерно распределен по тонкому кольцу радиусом R. В какой точке на оси кольца напряженность поля максимальна? Ответ указать с точностью до трех значащих цифр.

Решение Выделим на кольце бесконечно малый элемент длиной dl , несущий на себе заряд dq (на рисунке показаны два таких заряда dq и / dq , равные по модулю и расположенные диаметрально противоположно), и определим напряженность, создаваемого им электрического поля в точке C , удалённой на расстояние r . Заряд dq можно считать точечным и поле этого заряда рассчитать по формуле: 2 4 0 1 r dq dE   (1) где 12 0 8,85 10    Ф/м – электрическая постоянная;  – диэлектрическая проницаемость среды; r – расстояние от заряда dq до точки С. Векторы напряжённости электрического поля каждого из этих зарядов одинаковы по модулю и направлены так, что концы этих векторов образуют конус с вершиной в точке С (штриховой линией показано основание этого конуса). Проекции этих векторов на плоскость кольца компенсируются, поэтому суммарный вектор направлен вдоль оси z . Из рисунка можем записать: dEz  dEcos (2)