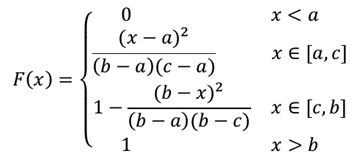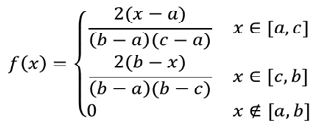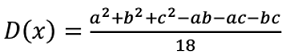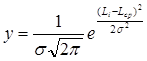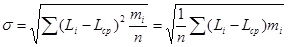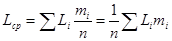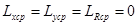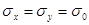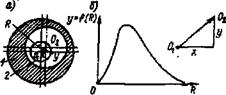
Закон симпсона равнобедренного треугольника

К распределению по закону Симпсона приводит сложение двух случайных величин, подчиненных закону равной вероятности при одинаковых параметрах рассеяния. Кривая рассеяния имеет вид равнобедренного треугольника (рис. 1.27), из-за чего закон Симпсона часто называют законом треугольника.

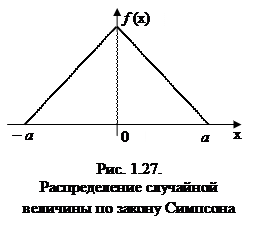
При выборе в качестве начала отсчета случайной величины ее плотность распределения и математическое ожидание имеют следующий вид:

, (1.63)

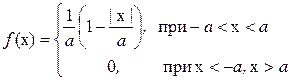
M_x = 0 , 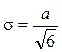, . (1.64)

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 9137 – | 7300 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Функция треугольного распределения случайной величины определяется формулой:

Плотность треугольного распределения СВ находится по формуле:

Математическое ожидание — формула:

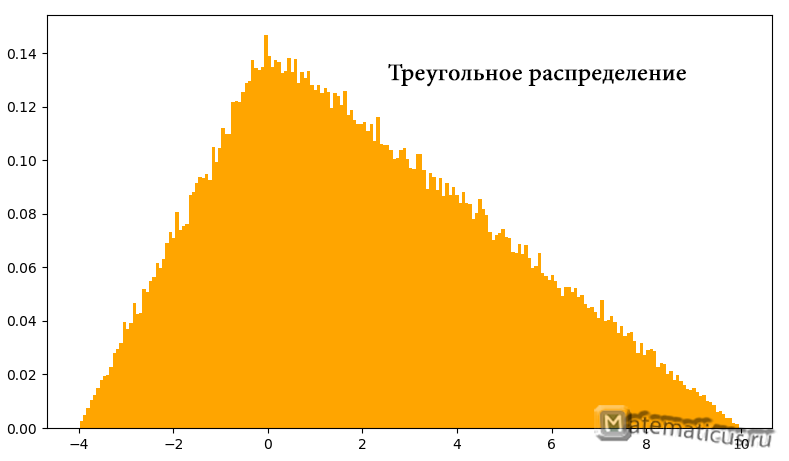
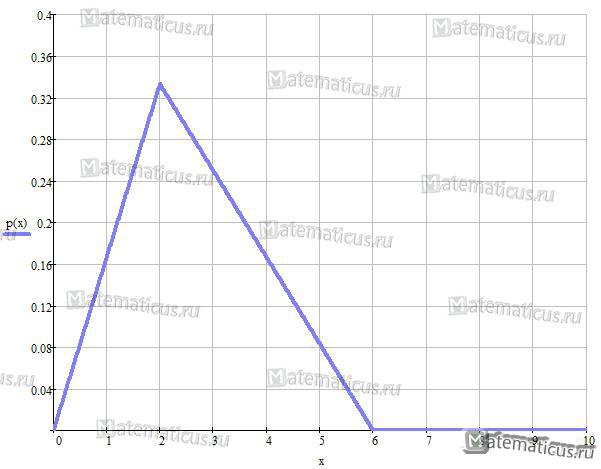
График плотности треугольного распределения случайной величины в диапазоне от -4 до 10

График плотности треугольного распределения случайной величины

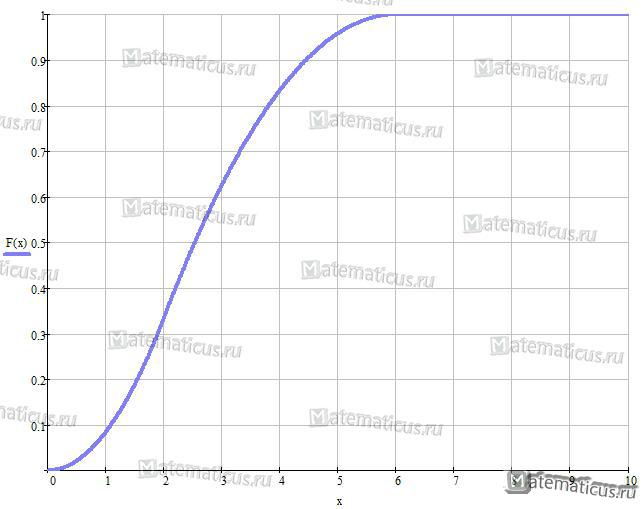
График функции треугольного распределения случайной величины

Треугольное распределения является приблизительной моделью и применяется, когда недостаточно данных или они отсутствуют. Треугольный закон распределения также используется для построения сложных законов распределения.

Он характерен для случайных погрешностей цифровых приборов, в которых измеряемая величина преобразуется в пропорциональный интервал времени Т_сч, называемый временем счета, а измерение этого интервала выполняется с помощью счетных импульсов стабильного генератора, имеющих период следования Т . В связи со случайным положением счетных импульсов относительно интервала Т_сч, а также случайным соотношением между периодом Т и временем счета Т_сч треугольный закон представляет собой композицию (объединение) двух равномерных законов с одинаковыми по величине максимальными погрешностями.

Функция распределения одномерной плотности вероятности случайных погрешностей для треугольного закона задается следующими соотношениями:

(46)где

График треугольного закона распределения приведен на рисунке 20.

Математическое ожидание величины x: определяется по той же формуле, что и равномерное:

Рисунок 20 – Треугольное распределение случайной величины

Среднее квадратическое отклонение определяется по формуле:

Теория вероятностей (стр. 13 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Определение. Начальным моментом k-го порядка (k = 0, 1, 2, …) распределения случайной величины Х (если он существует) называется действительное число ак, определяемое формулой:

. (5.11)

ния случайной величины Х (если он существует) называется действительное число , определяемое по формуле:

. (5.12)

Из определения моментов следует, что

, , , , .

Отметим еще две важные характеристики распределения, связанные с моментами высшего порядка: (коэффициент асимметрии или «скошенности» распределения), (коэффициент эксцесса, (просто «эксцесс») или “островершинности” распределения).

Пример 1. Случайная величина Х подчинена закону распределения Парето с параметрами , , если ее функция распределения вероятностей имеет вид:

Найти основные характеристики , , Mo, Mе распределения Парето, выразив их через параметры распределения.

Решение. Находим плотность распределения вероятностей:

Математическое ожидание вычислим по формуле (5.8):

, .

Найдем второй начальный момент:

, а > 2.

Для вычисления дисперсии используем формулу:

.

Так как плотность вероятности f(x) монотонно убывает при х >, то М0 =.

Медиану Ме находим, как корень уравнения , откуда .

Пример 2. Случайная величина Х распределена по закону рав­нобедренного треугольника в интервале (-а; а) (закон Симпсона), если она непрерывного типа и ее плотность распределения вероятностей имеет вид, изображенный на рис. 14.

Написать выражение для f(x), вычислить функцию распределе­ния вероятностей, математическое ожидание, дисперсию, моду, ме­диану, эксцесс.

f(x)

1/a

Найдем плотность вероятностей, используя уравнение прямой в отрезках: f(x) = 0, если ха; или , если а a.

0, если

F(x) =

1, если = 0 и функция f(x) на интервале (-а; а) четна, а вне этого интервала равна нулю, то

Поступая аналогично и используя формулу (5.12), вычислим центральный момент четвертого порядка:

,

5.4. Примеры некоторых классических распределений

1. Закон равномерной плотности

В некоторых задачах практики встречаются непрерывные вели­чины, которые в пределах некоторого конечного интервала имеют постоянную плотность вероятностей. О таких случайных величинах говорят, что они распределяются по закону равномерной плотности.

Пример 1. Производится взвешивание тела на точных весах, но в распоряжении взвешивающего имеются только разновески весом не менее 1 г; результат взвешивания показывает, что вес тела заключен между а и (а + 1) граммами. Вес тела принят равным (а + 0,5) граммам. Допущенная при этом ошибка X, очевидно, есть случайная величи­на, распределенная c равномерной плотностью на интервале (-0,5; 0,5) г.

Пример 2. Пригородные поезда идут с интервалом 10 минут. Пассажир выходит на платформу в случайный момент времени. Время Т, в течение которого ему придется ждать поезда, представля­ет собой случайную величину, распределенную с равномерной плот­ностью на интервале (0; 10) минут.

Рассмотрим случайную величину X, подчиненную закону рав­номерной плотности на интервале от а до b, и напишем для нее выражение плотности распределения f(x).

Так как

а площадь, ограниченная графиком f(x) и осью абсцисс, равна еди­нице: с(b — а) = 1, то

и плотность распределения f(x) имеет вид:

(5.13)

Напишем выражение для функции распределения F(x), исполь­зуя формулу (5.6):

(5.14)

График функции F(x) приведен на рис. 15.

Определим числовые характеристики случайной величины X, имеющей равномерное распределение на интервале от а до b. Мате­матическое ожидание величины Х равно: .

В силу симметрии равномерного распределения медиана величины Х также равна Ме =.

Моды закон равномерной плотности не имеет.

По формуле (5.10) находим дисперсию X:

откуда среднее квадратическое отклонение

.

В силу симметрии распределения его асимметрия равна нулю:

F(x)

1

Для определения эксцесса находим четвертый центральный мо­мент:

, отсюда

.

Функцию R(t) называют функцией надежности (она определяет вероятность безотказной работы элемента за время t).

Часто функция F(t) имеет показательное распределение, функ­ция распределения которого F(t)=1— .

Следовательно, функция надежности R(t) имеет вид:

Показательным законом надежности называют функцию надеж­ности R(t), определяемую равенством

где – интенсивность отказов.

Пример 1. Непрерывная случайная величина Х распределена по показательному закону f(x) = 5 (х 0). Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X.

Решение. Так как М(Х) и a(Х) показательного распределения равны между собой и равны числу 1/ – параметру показательного распределения, то . Дисперсия D(X) = (0,2)2 = 0,04.

Пример 2. Время безотказной работы элемента, распределенного по показательному закону f(x) = 0,05е-0,05t (t > 0), где t – время в сутках. Найти вероятность того, что элемент проработает 20 суток.

Решение. По условию постоянная интенсивность отказов = 0,05. Далее по формуле (5.16) определим искомую вероятность R(20) = e-0,05*20 = e-10,37.

1. Распределение Вейбулла

Случайная величина Х непрерывного типа подчиняется закону распределения Вейбулла с параметрами a R, b > 0, если ее плотность распределения вероятностей записывается в виде

Распределение Вейбулла в ряде случаев характеризует срок службы радиоэлектронной аппаратуры и, кроме того, применяется для аппроксимации различных несимметричных распределений в математической статистике. Легко заметить то, что показательное распределение – частный случай распределения Вейбулла (n = 1, а = 0, b = 1/ ).

Вычислим математическое ожидание случайной величины X, имеющей распределение Вейбулла.

Сделаем подстановку , отсюда , , нижний предел интегрирования по переменной t равен 0, а верхний равен

и, следовательно,

Первый из полученных интегралов равен 1, а второй

где – гамма-функция Эйлера. Итак,

.

Непрерывная случайная величина Х имеет гамма-распределение с параметрами, а > 0 и b > 0, если ее плотность вероятностей имеет сле­дующий вид:

Показательное распределение с параметром также является частным случаем гамма-распределения (а = 1, b =).

Другой частный случай гамма-распределения с параметрами

(n – натуральное число ), называется распределением Хи-квадрат с n степенями свободы (пишут X2(n)). Распределение Х2(n) играет большую роль в математической статистике.

Если случайная величина Х подчинена закону Х2(n), то ее плот­ность вероятностей записывается в виде

Законы рассеяния (распределения) размеров

В результате возникновения случайных погрешностей при обработке партии заготовок на настроенном станке истинный размер каждой заготовки является случай величиной и может принимать любое значение в границах определенного интервала.

Совокупность значений истинных размеров заготовок, обработанных неизменных условиях и расположенных в возрастающем порядке с указанием частоты повторения этих размеров или частостей, называется распределением размеров заготовок. Под частостью понимается отношение числа заготовок одного размера к общему числу заготовок партии.

Распределение размеров заготовок можно представить в виде таблиц или графиков. На практике измеренные значения истинных размеров заготовок разбивают на интерн или разряды таким образом, чтобы цена интервала (разность между наибольшим и наименьшим размерами в пределах одного интервала) была несколько больше и деления шкалы измерительного устройства. Этим компенсируются погрешности измерения. Частость в этом случае представляет собой отношение числа m заготовок действительные размеры которых попали в данный интервал, к общему количеству n измеренных заготовок партии.

Например, после измерения 100 шт. заготовок с действительными размерами в пределах от 20,00 до 20,35 мм распределение размеров этих заготовок может иметь приведенный в табл. 3.3.

Распределение размеров заготовок

Интервал, мм	Частота т	Частость rn/n
20,00-20,05	0,02
20,05-20,10	0,11
20,10-20,15	0,19
20,15-20,20	0,28
20,20-20,25	0,22
20,25-20,30	0,15
20,30-20,35	0,03
Итого:	п =2Г-т = 100	JET т/п

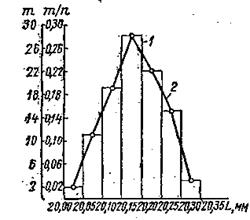
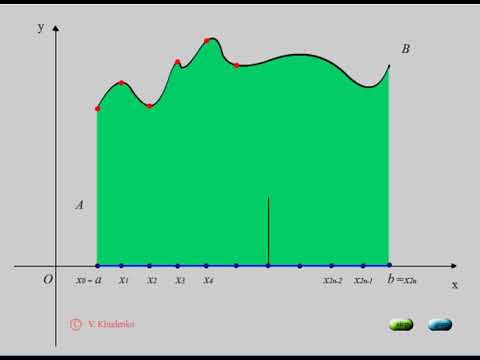
Рис. 3.9 Распределение измеренных размеров заготовок

Распределение измеренных размеров таких заготовок можно представтъ в графика (рис.3. 9). По оси абсцисс откладывают интервалы размеров в соответственно табл.3. 3, а по оси ординат соответствующие им частоты т или частоты т п. В результате построения получается ступенчатая линия 1, называемая гистограммы! распределения. Если последовательно соединить между собой точки, соответствующие середине каждого интервала, то образуется ломаная кривая, которая носит название эмпирической кривой распределения, или полигона 2 распределения. При значительном количестве замере заготовок и большом числе интервалов размеров ломаная эмпирическая кривая приближается по форме к плавной кривой, именуемой кривой распределения, построения гистограммного распределения рекомендуется измеренные размеры разбивать не менее чем на шесть интервалов при общем числе измеряемых заготовок не меньше 50 шт.

При разных условиях обработки заготовок рассеяние их истинных размеров подчиняется различным математическим законам. В технологии машиностроения большое практическое значение имеют следующие законы: нормального распределения (закон Гаусса), равнобедренного треугольника (закон Симпсона). эксцентриситета (закон Релея), законы равной вероятности и функции распределения, представляющие с композицию этих законов.

Закон нормального распределения(закон Гаусса).

Многочисленные исследования, проведенные профессорами А.Б. Яхиным, А.А. Зыковым и другими, показали, что распределение действительных размеров заготовок, обработанных на настроенных станках, очень часто подчиняется закону нормального распределения (закону Гаусса).

Это объясняется известным положением теории вероятностей о том, распределение суммы большого числа взаимно независимых случайных слагаемых величин (при ничтожно малом и примерно одинаковом влиянии каждой из них на общую сумму и при отсутствии влияния доминирующих факторов) подчиняется закону нормального распределения Гаусса.

Результирующая погрешность обработки обычно формируется в результате одновременного воздействия большого числа погрешностей, зависящих от станка, приспособления, инструмента и заготовки, которые по существу представляют с взаимно независимые случайные величины; влияние каждой из них на результирующую погрешность имеет один порядок, поэтому распределение результирующей погрепп обработки, а значит, и распределение действительных размеров обрабатываемых заготовок подчиняются закону нормального распределения.

Уравнение кривой нормального распределения имеет следующий вид:

где σ — среднее квадратическое отклонение, определяемое по формуле:

Li — текущий действительный размер; Lcp — среднее взвешенное арифметическое значение действительных размеров заготовок данной партии. Значение Lcp можно определить из выражения:

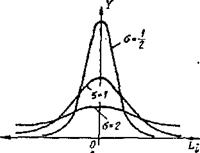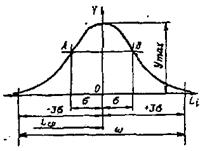
Рис.3.10. Кривая нормального распределения (закон Гаусса)

Рис.3.11 Влияние среднего квадратического отклонения на форму кривой нормального распределения

где m_i — частота (количество заготовок данного интервала размеров); n — количество заготовок в партии.

Кривая, характеризующая дифференциальный закон нормального распределения, показана на рис.3.10. Среднее арифметическое Lcp действительных размеров заготовок данной партии характеризует положение центра группирования размеров.

Анализ уравнения (3.2) показывает, что кривая нормального распределения симметрична относительно оси ординат. Значениям х и -х соответствует одинаковая величина ординаты у. При Li = Lcp кривая имеет максимум, равный:

(3.5)

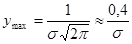
На расстоянии ±σ от вершины кривая имеет две точки перегиба (точки А и В). Ордината точек перегиба:

(3.6)

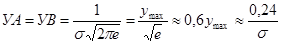
Кривая ассимптотически приближается к оси абсцисс. На расстоянии ±3σ от положения вершины кривой ее ветви так близко подходят к оси абсцисс, что в этих пределах оказывается 99,73% площади, заключенной между всей кривой нормального распределения с осью абсцисс, ограничивая 100% площади между кривой и осью абсцисс. Возникающая при этом допущении погрешность, составляющая 0,27%, практического значения не имеет.

При увеличении σ значение ординаты у^ уменьшается (см. формулу 3.9), а поле рассеяния о = 6а возрастает; в результате этого кривая становится более пологой и низкой, что свидетельствует о большем рассеянии размеров и, следовательно, о меньшей точности. В этом смысле среднее квадратическое отклонение а является мерой рассеяния или мерой точности. Влияние σ на форму кривой нормального распределения показано на рис.3.11.

Фактическое поле рассеяния размеров заготовок ω = 6σ

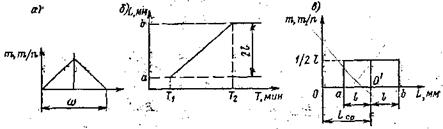
Закон равнобедренного треугольника (закон Симпсона). При обработке заготовок с точностью 7-го и 8-го, а в некоторых случаях и 6-го квалитетов распределение их размеров в большинстве случаев подчиняется закону Симпсона, который графически выражается равнобедренным треугольником (рис.3.15, а) с полем рассеяния

(3.7)

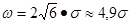
Величина среднего квадратического отклонения σ и в этом случае определяется по формуле (3.3).

—

Рис.3.12 Распределение размеров обработанных заготовок по закону Симпсона а) и по закону равной вероятности б), в)

Закон равной вероятности. Если рассеяние размеров зависит только от переменных систематических погрешностей (например, от износа режущего инструмента), то распределение действительных размеров партии обработанных заготовок подчиняется закону равной вероятности.

Например, при установившемся износе режущего инструмента уменьшение его размеров во времени подчиняется прямолинейному закону, что соответственно увеличивает (при обработке валов) или уменьшает (при обработке отверстий) диаметры обрабатываемых заготовок

Естественно, что изменение размеров обрабатываемых заготовок на величину 21 = b — а за период Т2 — Т1 в этом случае тоже происходит по закону прямой линии (рис.3.12, б). Распределение размеров заготовок в интервале от а до b по закону равной вероятности выражается прямоугольником (рис.3.12, в) с основанием 21 и высотой (ординатой) 1/21.

Площадь прямоугольника равна единице что означает 100%-ную вероятность появления размера заготовки в

интервале от а до Ь.

Среднее арифметическое значение размера:

(3.8)

(3.9)

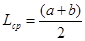
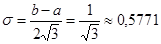
Фактическое поле рассеяния:

(3.10)

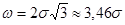
Закон равной вероятности распространяется на распределение размеров заготовок повышенной точности (5-6-й квалитеты и выше) при их обработке по методу пробных ходов. Из-за сложности получения размеров очень высокой точности вероятность попадания размера заготовки в узкие границы допуска по среднему, наибольшему или наименьшему его значению становится одинаковой.

Закон эксцентриситета (закон Релея). Распределение таких существенно положительных величин, как эксцентриситет, биение, разностенность, непараллельность, неперпендикулярность, овальность, конусообразность и некоторых других, характеризующихся их абсолютными значениями (то есть без учета знака), подчиняется закону распределения эксцентриситета (закону Релея).

Распределение по закону Релея формируется (в частности) тогда, когда случайная величина R является радиус-вектором при двумерном гауссовом распределении, то есть если она представляет собой геометрическую сумму двух. случайных величин х и у

, (3.11)

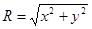
каждая из которых подчиняется закону Гаусса с параметрами:

Закон распределения Релея однопараметрический, и уравнение его кривой распределения имеет вид

(3.12)

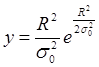
где σ₀ — среднее квадратическое отклонение значении координат х и у.

На рис.3.13, б) показано, что для теоретической кривой распределения по закону Релея характерны крутой подъем восходящей ветви и более пологий спуск нисходящей ветви. Вершина кривой более заострена, чем у кривой нормального распределения, и смещена от среднего значения переменной величины R в сторону начала координат.

Из уравнения (3.12) следует, что при R=0 и у=0, то есть начало кривой распределения эксцентриситета совпадает с началом координат. Нисходящая ветвь этой кривой асимптотически приближается к оси абсцисс.

Рис.3.13. Образование эксцентриситета (радиуса-вектора R) втулки 1 при ее обработке на цилиндрической оправке 2 при различии зазора между оправкой и отверстием втулки (а) и функции y=f (R) распределения размеров по закону Релея (б).

🔥 Видео