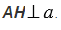Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Определение перпендикулярности прямой и плоскости
Каким будет определение положения прямой и плоскости, зависит от наличия общих точек. Если их больше одной, то прямая лежит на данной плоскости, если одна — то она ее пересекает. Если прямая не имеет с плоскостью точек пересечения, то прямая и плоскость параллельны.
Пересечение прямой линии и плоскости может происходить под разными углами. Если при пересечении между прямой и плоскостью образуется прямой угол, то такая прямая является к плоскости перпендикуляром. При этом она перпендикулярна всем прямым линиям, принадлежащим данной плоскости. Из этого свойства вытекает следующее определение.
Перпендикулярной к плоскости называется прямая линия, которая перпендикулярна всем без исключения прямым, лежащим в выбранной плоскости.
Следствием из данного определения является свойство плоскости, для которой установлено наличие перпендикуляра. Оно формулируется следующим образом: «Если плоскость перпендикулярна некоторой прямой, то она является также перпендикулярной для всех прямых, параллельных данной прямой».
В решении задач на построение перпендикуляров к плоскости в конкретной точке существует только одно решение, поскольку через определенную точку можно провести только одну прямую, занимающую по отношению к плоскости перпендикулярное положение.
О единственности такой прямой в геометрии существует доказательство.
Видео:7 класс, 16 урок, Перпендикуляр к прямойСкачать

Проведение перпендикуляра из точки к прямой
В жизни с перпендикуляром можно столкнуться часто. Например, если по двум параллельным направляющим движутся тела, то кратчайшее расстояние между ними будет лежать именно по перпендикуляру.
Допустим, на уроке ученикам дали задание построить перпендикуляр к имеющейся площади. Особым условием является то, что проходить этот перпендикуляр должен через выбранную точку. Технически задача проста. Для ее исполнения нужен чертежный треугольник, один угол у которого является прямым, то есть составляет 90°.
Приложив его к прямой таким образом, что одна из сторон, образующих прямой угол, лежит на прямой, а другая — проходит через точку с определенными координатами, необходимо соединить эту точку и прямую.
Такой отрезок будет кратчайшим соединением точки с прямой линией (и выбранной плоскостью).
Взаимное положение такого перпендикуляра и прямой обозначается специальным знаком.
Для перпендикуляра, проведенного из выбранной точки к прямой, можно определить длину. Она равна расстоянию от этой точки до точки пересечения с прямой плоскостью.
Видео:Наклонная, проекция, перпендикуляр. 7 класс.Скачать

Как построить перпендикуляр к прямой
Построить перпендикуляр к прямой можно несколькими способами:
1. С помощью циркуля.
Из выбранной точки P проводим полуокружность, которая пересекается с прямой в точках A и B.
Затем тем же радиусом строим две окружности, центры которых совпадают с точками A и B. При этом окружности проходят через точку P.
Следующим шагом будет соединение точек P и Q.
На данном рисунке перпендикуляр к прямой AB — отрезок PQ.
2. Вторым способом построения перпендикуляра является использование транспортира. Чтобы провести перпендикуляр, внимательно откладываем 90° от выбранной точки на прямой, используя при этом линейку транспортира. Отрезок, соединяющий эту точку и деление 90°, является перпендикуляром к прямой в заданной точке.
3. Третий способ был описан выше. Он основан на применении чертежного треугольника и линейки. С помощью линейки проводим прямую. Прикладываем к ней прямым углом треугольник и очерчиваем этот угол с двух сторон. Один отрезок совпадает с имеющейся прямой, а второй является перпендикуляром к ней.
Видео:Перпендикуляр от точки к плоскостиСкачать
Пояснение на примерах
В конспектах по геометрии присутствует понятие высоты, представляющей собой перпендикуляр к одной из сторон геометрической фигуры (например, треугольника).
Высотой треугольника называется перпендикуляр, который выходит из вершины треугольника и следует к противоположной стороне (либо к продолжению этой стороны, если треугольник тупоугольный).
В данном определении содержится отличие от основной характеристики биссектрисы, которая, опускаясь на противолежащую углу сторону, не является перпендикуляром к ней.
Аналогичная ситуация с определением медианы — линии, исходящей из угла треугольника и делящей противоположную сторону на две равные части.
Высоту треугольника можно провести из любого его угла, поэтому у каждого треугольника имеется три высоты.
Существует теорема, что все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром.
Используя свойство высоты треугольника о пересечении одной из его сторон под прямым углом, можно через высоту выразить формулу площади треугольника:
Уравнение для расчета высоты через площадь:
Найти через длины сторон:
h a = 2 p p — a p — b p — c a
где p — это полупериметр треугольника, который рассчитывается так:
p = a + b + c 2
Можно дать краткую характеристику еще двум способам выразить высоту треугольника:
4. Через длину прилежащей стороны и синус угла
h a = b sin y = c sin β
5. Через стороны и радиус описанной окружности
Видео:Перпендикулярные прямые. 6 класс.Скачать

Треугольник и его виды. Элементы треугольника
Треугольник – это геометрическая фигура, состоящая из трех точек, попарно соединенных между собой отрезками. Точки называются вершинами треугольника, отрезки – сторонами треугольника. Треугольник имеет три вершины и три стороны. Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.
Внутренние углы треугольника – это углы, образованные его сторонами. Угол А – это угол, образованный сторонами АВ и АС.
Виды треугольников по углам:
- Остроугольный треугольник – это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º).
- Прямоугольный треугольник – это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).
- Тупоугольный треугольник – это треугольник, у которого один угол тупой (то есть имеет градусную меру больше 90º).
Виды треугольников по сторонам:
- Равносторонний треугольник (или правильный треугольник) – это треугольник, у которого все три стороны равны.
- Равнобедренный треугольник – это треугольник, у которого две стороны равны.
- Разносторонний треугольник – треугольник, все стороны которого имеют разную длину.
Элементы треугольника
Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Любой треугольник имеет три медианы, которые пересекаются в одной точке. Эта точка пересечения называется центроидом или центром тяжести треугольника. Центроид делит каждую медиану в отношении 1:2, считая от основания медианы.
Биссектриса – это отрезок, делящий угол треугольника на две равные части. Любой треугольник имеет три биссектрисы, которые пересекаются в одной точке.
Высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. Любой треугольник имеет три высоты, которые пересекаются в одной точке, называемой ортоцентром треугольника.
Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.
Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине: (MN=frac12AC; MNparallel AC) .
Серединный перпендикуляр к отрезку – прямая, перпендикулярная к этому отрезку и проходящая через его середину. Три срединных перпендикуляра треугольника пересекаются в одной точке, являющейся центром описанного круга.
Основные свойства треугольников
- Против большей стороны лежит больший угол, и наоборот.
- Против равных сторон лежат равные углы, и наоборот. В частности, все углы в равностороннем треугольнике равны.
- Сумма углов треугольника равна 180º. Из двух последних свойств следует, что каждый угол в равностороннем треугольнике равен 60º.
- Продолжая одну из сторон треугольника, получаем внешний угол. Внешний угол треугольника равен сумме внутренних углов, не смежных с ним.
- Любая сторона треугольника меньше суммы двух других сторон и больше их разности (a b – c; b a – c; c a – b).
Один из внешних углов треугольника равен 65 (^circ) . Углы, не смежные с данным внешним углом, относятся как 6:7. Найдите наибольший из них.
Внутренние углы треугольника относятся как 3:7:8. Найдите отношение внешних углов треугольника.
Чему равна градусная мера одного из углов прямоугольного треугольника?
Если в треугольнике один угол больше суммы двух других углов, то он
Если в треугольнике один внешний угол острый, то этот треугольник
Периметр равнобедренного треугольника равен 11 см, а основание равно 3 см. Найдите боковую сторону треугольника.
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Перпендикулярные прямые
Перпендикулярные прямые — это две пересекающиеся прямые,
образующие четыре прямых угла.
По другому можно сказать так: перпендикулярные
прямые — это две прямые, которые пересекаются под прямым углом.
Эти два утверждения истинны.
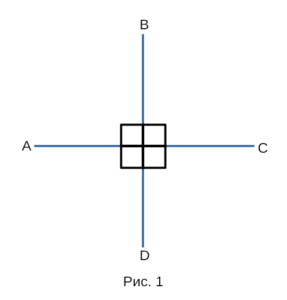
Перпендикулярность прямых обозначается символом ⊥ . Например,
перпендикулярность прямых, изображенных на рисунке 1 обозначается
так: AC ⊥ BD. А читается так: прямая AC перпендикулярна к прямой BD.
Для того, чтобы начертить перпендикулярные прямые используют
чертежный угольник и линейку.
Две прямые, перпендикулярные к третьей не пересекаются,
но параллельны между собой.
- Перпендикуляр — это прямая опущенная под прямым углом
к другой прямой. - Перпендикуляр к данной прямой — это отрезок прямой,
перпендикулярный данной прямой, имеющий одним из
своих концов их точку пересечения. - Основание перпендикуляра — это конец отрезка прямой,
которая перпендикулярна данной прямой.
Условие перпендикулярности двух прямых — две прямые
пересекаются под прямым углом.
Из точки, не лежащей на прямой, можно провести
перпендикуляр к этой прямой, и притом только один.
Прямая перпендикулярна плоскости, если она
перпендикулярна любой прямой, лежащей
в этой плоскости.
💥 Видео
Геометрия 7 класс (Урок№11 - Перпендикуляр к прямой.)Скачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Перпендикулярные прямыеСкачать

7 класс, 12 урок, Перпендикулярные прямыеСкачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Наклонная, проекция, перпендикуляр и их свойства. 7 класс.Скачать

Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

Перпендикуляр и наклонная в пространстве. 10 класс.Скачать

Геометрия. 7 класс. Теоремы. Т4. Перпендикуляр к прямой.Скачать

8 класс, 36 урок, Свойства серединного перпендикуляра к отрезкуСкачать

Серединные перпендикуляры в треугольникеСкачать
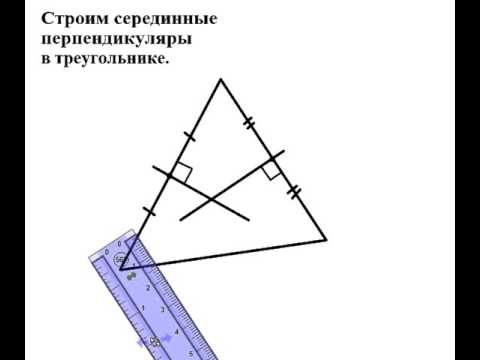
7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Наклонная, проекция, перпендикуляр и их свойства. Практическая часть. 7 класс.Скачать

Перпендикуляр к прямой | Геометрия 7-9 класс #17 | ИнфоурокСкачать