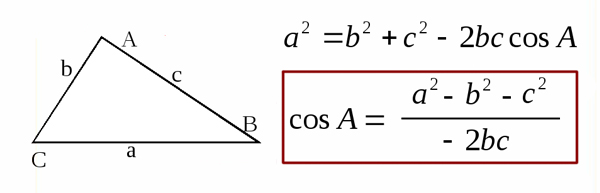Задание 9 егэ информатика треугольник

Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа.

Определите, сколько среди заданных троек чисел таких, которые могут быть сторонами прямоугольного треугольника.

Заметим, что треугольник является прямоугольным, если квадрат длины гипотенузы треугольника будет равен сумме квадратов длин катетов этого треугольника. Тогда в ячейке D1 запишем формулу =(МАКС(A1:C1))^2 и скопируем её во все ячейки диапазона D2:D5000. В ячейке E1 запишем формулу

и скопируем её во все ячейки диапазона E2:E5000. Таким образом, получим квадрат длины гипотенузы и сумму квадратов катетов для каждой тройки чисел. После этого в ячейку F1 запишем формулу =ЕСЛИ(D1=E1;1;0) и скопируем её во все ячейки диапазона F2:F5000. Теперь, воспользовавшись формулой =СУММ(F1:F5000), получим ответ — 2.

Видео:КАК решить 9 НОМЕР на PYTHON | ПРОЩЕ, чем в Excel | ЕГЭ Информатика 2023Скачать

ЕГЭ по информатике 2022 — Задание 9 (Электронная таблица)

Девятое задание из ЕГЭ по информатике 2022 проверяет умение обрабатывать числовую информацию с помощью таблиц Excel.

При подготовке к 9 заданию из ЕГЭ по информатике может быть полезна и прошлогодняя статья.

В 2022 году пошла тенденция давать задачи, в которых применяются знания по математике и геометрии.

Задача (Равнобедренный треугольник)

(№ 4335) (А. Богданов) Откройте файл электронной таблицы 9-114.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться сторонами равнобедренного треугольника. В ответе запишите только число.

Для каждой тройки проверим:

• Являются ли числа сторонами треугольника.
• Есть ли среди трёх чисел два равных числа.

Чтобы проверить первое условие, нужно вспомнить неравенство треугольника: любая сторона треугольника должна быть меньше суммы двух других сторон.

Поставим «1» в столбце D напротив тех троек, которые подходят под первое условие.

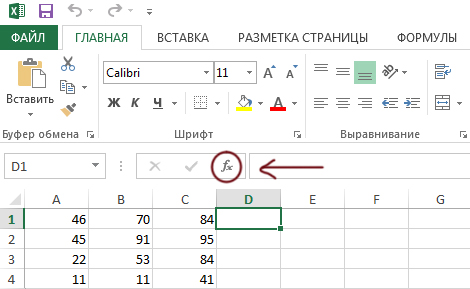
Сначала напишем формулу для первой строчки в ячейке D1.

Кликаем в ячейку D1 и нажимаем кнопку Вставить функцию.

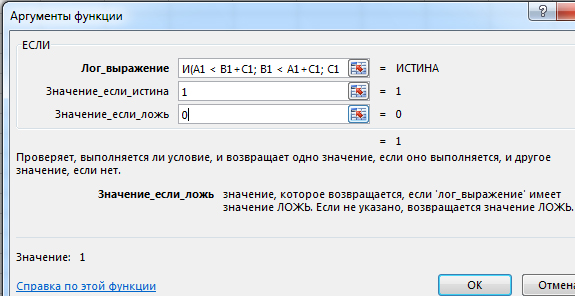
Выбираем функцию ЕСЛИ. Пишем логическое выражение:

Союз И говорит о том, что три условия должны сработать одновременно.

В Значение_если_истина ставим 1. В Значение_если_ложь ставим 0.

Если одновременно выполняются три условия, то в ячейку идёт 1, иначе 0.

Распространим формулу на весь столбец. Подведём курсор к правому нижнему углу. Как только загорелся чёрный крестик, кликаем два раза, и формула должна распространится на весь столбец.

Возле тех строчек, которые удовлетворяют условию, будут нули, возле тех, которые не удовлетворяют, будут единицы.

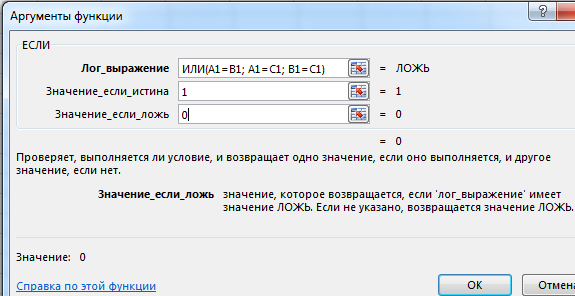
За второе условие будет отвечать столбец E. Напишем условие в ячейку E1.

Союз ИЛИ говорит о том, что если одно условие сработает, значит, выражение будет считаться истинным.

В Значение_если_истина ставим 1. В Значение_если_ложь ставим 0.

Распространяем всю формулу на весь столбец E. Напротив тех строчек, которые удовлетворяют второму условию, будут стоять «1», в противном случае «0».

В столбце F ставим «1» в тех строчках, где в столбцах D И E одновременно «1», используя функцию ЕСЛИ.

В Значение_если_истина ставим 1. В Значение_если_ложь ставим 0.

Выделив столбец F, в правом нижнем углу посмотрим сумму единиц в этом столбце.

Получается ответ 229.

Ещё одна тренировочная задача из ЕГЭ по информатике 2022.

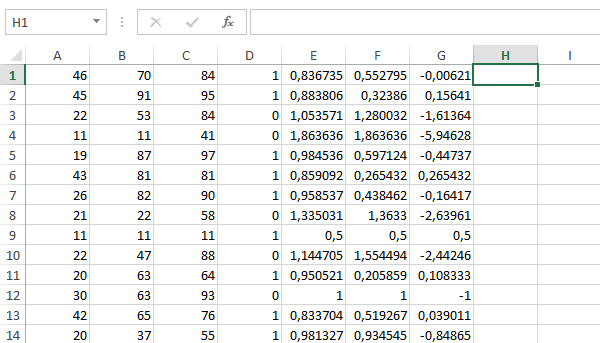
(А. Богданов) Откройте файл электронной таблицы 9-114.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться сторонами тупоугольного треугольника. В ответе запишите только число.

Во-первых проверим: удовлетворяют ли числа условию неравенства треугольника (аналогично прошлой задаче). За это будет отвечать столбец D.

В столбцах E, F, G мы будем вычислять косинусы трёх углов треугольника. Косинусы будем находить по теореме косинусов. Косинусы будем вычислять для всех троек, но учитывать только те, где выполняется неравенство треугольника.

В ячейке E1 напишем формулу:

В ячейке F1 напишем формулу:

В ячейке G1 напишем формулу:

Распространим вышеуказанные формулы на соответствующие столбцы.

Получается примерно такая картина:

Остался последний шаг: проверить, есть ли у какой-нибудь тройки, которая удовлетворяет неравенству треугольника, отрицательный косинус. Тупой угол имеет отрицательный косинус.

Кликаем в ячейку H1, нажимаем кнопку «Вставить функцию» и выбираем ЕСЛИ.

В поле Лог_выражение пишем:

В поле Значение_если_истина ставим «1», в поле Значение_если_ложь ставим «0». Распространяем формулу на весь столбец H, и посчитаем количество единиц в этом столбце.

Количество единиц равно 1720.

Снова нужно знать математические формулы в следующей задаче из примерных вариантов ЕГЭ по информатике 2022.

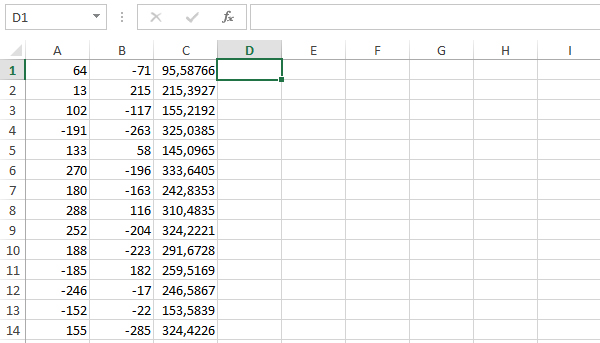
(А. Комков) Откройте файл электронной таблицы 9-103.xls, содержащей в каждой строке два целых числа – координаты точки на плоскости. Найдите наибольшее расстояние точки от начала координат. В ответе запишите целую часть найденного расстояния.

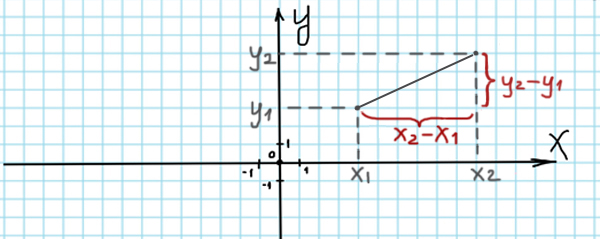
Посмотрим, как найти расстояние от точки с координатами (x1, y1) до точки с координатами (x2, y2).

Здесь работает теорема Пифагора. Здесь s — расстояние между двумя точками.

s 2 = (x2-x1) 2 + (y2-y1) 2

В нашей задаче первая точка — это начало координат, следовательно, x1=0 и y1=0.

В столбце С получим расстояние от конкретной точки до начала координат.

В ячейке C1 напишем формулу и распространим эту формулу на весь столбец.

Найдём максимальное значение в столбце С. Теперь кликнем в ячейку D1. Нажмём кнопку «Вставить функцию». Выберем функцию МАКС. Укажем мышкой столбец С. Нажмём «ОК».

Целая часть получившегося числа равна 425.

(Е. Джобс) Откройте файл электронной таблицы 9-j1.xls, содержащей показатели высот над уровнем моря географических точек. Найдите среднее значение всех отрицательных показателей и максимальное положительное значение. В качестве ответа укажите целую часть суммы найденных значений.

Эта задача уже не связана c математическими аспектами. Здесь просто достаточно воспользоваться встроенными функциями Excel.

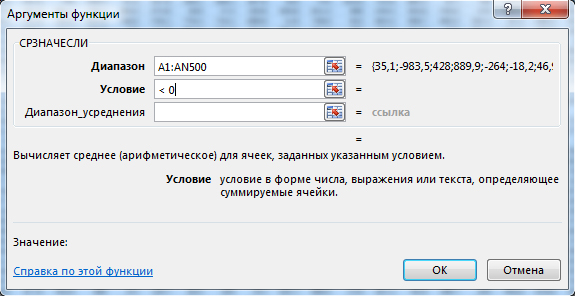
Нужно найти среднее значение только отрицательных значений. Для нахождения среднего значения есть функция СРЗНАЧ. Но нам нужно именно отрицательных значений. Для нахождения среднего значения с условием есть функция СРЗНАЧЕСЛИ. Щёлкним по пустой ячейки и вы

В поле Диапазон мы должны указать все ячейки. Это можно легко сделать с помощью мышки.

В поле Условие укажем »

Среднее значение примерно равно -497,47.

Для определения максимального значения, можно просто воспользоваться просто функцией МАКС, т.к. всё равно максимальное число будет положительным.

Максимальное значение получается 1000.

Сумма равна: 1000 + (-497,47) = 502,53

Целая часть равна 502.

Решим ещё одну old school’ную задачу, которая также полезна при изучении 9 задания из ЕГЭ по информатике 2022.

Электронная таблица содержит результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время измерений результат очередного измерения оказывался ниже результата предыдущего на 2 и более градусов.

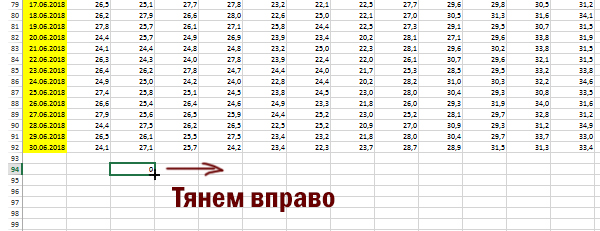
Внизу под числами представим мысленно область, где будет наше решение.

Таким образом, каждой ячейке соответствует своя ячейка в области решения.

Если выполняется условие задачи (т.е. предыдущее значение больше, чем данное значение на 2 и более градусов), то в соответствующей ячейке из области решения будет стоять «1», в противном случае «0».

Первая ячейка в каждой строчке нуждается в особой формуле, т.к. эта ячейка должна сравниваться с последней ячейкой предыдущей строчки.

Для остальных ячеек формула будет одинаковая, т.к. их значение сравнивается с предыдущем значение, т.е. с левой ячейкой.

Для первой ячейке не будем писать формулу, т.к. ей не с кем сравниваться.

Пишем формулу для строчек в ячейке C94:

Здесь используем функцию ЕСЛИ, как мы делали в предыдущих задачах.

Распространяем эту формулу на всю строчку.

И распространяем на всё пространство (кроме первого столбца)

Важно: Всего должно быть 91 строчка, как и в оригинале.

Теперь составим формулу для первого столбца. Кликаем в ячейку B95. И пропишем формулу:

Распространим данную формулу на весь столбец (на 91 строчку).

Осталось подсчитать количество единиц во всём рабочем пространстве, например, с помощью стандартной функции СУММ.

Количество единиц равно 458.

Видео:Таблицы / Эксель / Задания №9 и №3 | Информатика ЕГЭ 2023 | УмскулСкачать

Разбор задания №9 по информатике на ЕГЭ

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Сколь­ко се­кунд по­тре­бу­ет­ся мо­де­му, пе­ре­да­ю­ще­му со­об­ще­ния со ско­ро­стью 14400 бит/с, чтобы пе­ре­дать цвет­ное раст­ро­вое изоб­ра­же­ние раз­ме­ром 640 на 480 пик­се­лей, при усло­вии, что цвет каж­до­го пик­се­ля ко­ди­ру­ет­ся 24 би­та­ми?
По­яс­не­ние.

Время t вы­чис­ля­ет­ся по фор­му­ле t = Q / q, где Q — объем файла, q — cко­рость пе­ре­да­чи дан­ных.

Один цвет за­ни­ма­ет один пик­сел, по­это­му Q = 640 * 480 * 24 бит = 7 372 800 бит.

t = 7 372 800 бит / 14 400 бит/с = 512 с.

Задание 9 № 2
Ско­рость пе­ре­да­чи дан­ных через мо­дем­ное со­еди­не­ние равна 51200 бит/с. Пе­ре­да­ча тек­сто­во­го файла через это со­еди­не­ние за­ня­ла 10 с. Опре­де­ли­те, сколь­ко сим­во­лов со­дер­жал пе­ре­дан­ный текст, если из­вест­но, что он был пред­став­лен в 16-бит­ной ко­ди­ров­ке Unicode.
По­яс­не­ние.

Объём ин­фор­ма­ции вы­чис­ля­ет­ся по фор­му­ле Q = q * t, где t — время пе­ре­да­чи q — cко­рость пе­ре­да­чи дан­ных. По­это­му

Q = 51200 бит/c * 10 c.

Каж­дый сим­вол в дан­ной ко­ди­ров­ке ко­ди­ру­ет­ся 16-ю би­та­ми. Сле­до­ва­тель­но, ко­ли­че­ство сим­во­лов опре­де­лит­ся так:

N = 2 9 * 1000 / 2 4 = 2 5 * 1000 = 32 000.

Задание 9 № 3
Про­из­во­дит­ся двух­ка­наль­ная (сте­рео) зву­ко­за­пись с ча­сто­той дис­кре­ти­за­ции 48 кГц и 32-бит­ным раз­ре­ше­ни­ем, ре­зуль­та­ты за­пи­сы­ва­ют­ся в файл, сжа­тие дан­ных не ис­поль­зу­ет­ся. Раз­мер файла с за­пи­сью не может пре­вы­шать 16 Мбайт. Какая из при­ведённых ниже ве­ли­чин наи­бо­лее близ­ка к мак­си­маль­но воз­мож­ной про­дол­жи­тель­но­сти за­пи­си?

Так как ча­сто­та дис­кре­ти­за­ции 48 кГц, то за одну се­кун­ду за­по­ми­на­ет­ся 48 000 зна­че­ний сиг­на­ла. Глу­би­на ко­ди­ро­ва­ния 32 бит, т. е. 4 байта. По­сколь­ку за­пись двух­ка­наль­ная, объём па­мя­ти, не­об­хо­ди­мый для хра­не­ния дан­ных од­но­го ка­на­ла, умно­жа­ет­ся на 2, по­это­му, так как раз­мер файла не может пре­вы­шать 16 Мбайт, один канал за­ни­ма­ет 8 Мбайт или 8·2 20 байт. Чтобы найти мак­си­маль­но воз­мож­ную про­дол­жи­тель­но­сть за­пи­си, не­об­хо­ди­мо раз­де­лить най­ден­ный ин­фор­ма­ци­он­ный объем на глу­би­ну ко­ди­ро­ва­ния и на ча­сто­ту дис­кре­ти­за­ции:

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Про­из­во­ди­лась че­ты­рех­ка­наль­ная (квад­ро) зву­ко­за­пись с ча­сто­той дис­кре­ти­за­ции 24 кГц и 16-бит­ным раз­ре­ше­ни­ем. В ре­зуль­та­те был по­лу­чен файл раз­ме­ром 1800 Мбайт, сжа­тие дан­ных не про­из­во­ди­лось. Опре­де­ли­те при­бли­зи­тель­но, сколь­ко минут про­из­во­ди­лась за­пись.

В ка­че­стве от­ве­та ука­жи­те бли­жай­шее к вре­ме­ни за­пи­си целое число минут.
По­яс­не­ние.

Так как ча­сто­та дис­кре­ти­за­ции 24 кГц, то за одну се­кун­ду за­по­ми­на­ет­ся 24000 зна­че­ний сиг­на­ла.

Глу­би­на ко­ди­ро­ва­ния 16 бита, т. е. 2 байта. Т. к. за­пись четырёхка­наль­ная, объём па­мя­ти, не­об­хо­ди­мый для хра­не­ния дан­ных од­но­го ка­на­ла, умно­жа­ет­ся на 4, по­это­му, так как по­тре­бо­ва­лось 1800 Мбайт, один канал за­ни­ма­ет 450 Мбайт или 450·2 20 байт. Чтобы найти время, в те­че­ние ко­то­ро­го про­во­ди­лась за­пись, не­об­хо­ди­мо раз­де­лить най­ден­ный ин­фор­ма­ци­он­ный объем на глу­би­ну ко­ди­ро­ва­ния и на ча­сто­ту дис­кре­ти­за­ции:

сек.

Тем самым, время за­пи­си при­мер­но равно 163,84 ми­ну­ты, что близ­ко к 164 ми­ну­там.

Задание 9 № 5
Про­из­во­ди­лась четырёхка­наль­ная (квад­ро) зву­ко­за­пись с ча­сто­той дис­кре­ти­за­ции 8 кГц и 32-бит­ным раз­ре­ше­ни­ем. В ре­зуль­та­те был по­лу­чен файл раз­ме­ром 16 Мбайт, сжа­тие дан­ных не про­из­во­ди­лось. Какая из при­ведённых ниже ве­ли­чин наи­бо­лее близ­ка ко вре­ме­ни, в те­че­ние ко­то­ро­го про­во­ди­лась за­пись?

Так как ча­сто­та дис­кре­ти­за­ции 8 кГц, то за одну се­кун­ду за­по­ми­на­ет­ся 8 000 зна­че­ний сиг­на­ла. Глу­би­на ко­ди­ро­ва­ния 32 бит, т. е. 4 байта. По­сколь­ку за­пись четырёхка­наль­ная, объём па­мя­ти, не­об­хо­ди­мый для хра­не­ния дан­ных од­но­го ка­на­ла, умно­жа­ет­ся на 4, по­это­му, так как раз­мер файла не может пре­вы­шать 16 Мбайт, один канал за­ни­ма­ет 4 Мбайт или 4·2 20 байт. Чтобы найти про­дол­жи­тель­но­сть за­пи­си, не­об­хо­ди­мо раз­де­лить най­ден­ный ин­фор­ма­ци­он­ный объем на глу­би­ну ко­ди­ро­ва­ния и на ча­сто­ту дис­кре­ти­за­ции:

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Задание 9 № 6
Ка­ко­во время (в ми­ну­тах) пе­ре­да­чи пол­но­го объ­е­ма дан­ных по ка­на­лу связи, если из­вест­но, что пе­ре­да­но 9000 Мбайт дан­ных, при­чем треть вре­ме­ни пе­ре­да­ча шла со ско­ро­стью 60 Мбит в се­кун­ду, а осталь­ное время — со ско­ро­стью 90 Мбит в се­кун­ду?
По­яс­не­ние.

Обо­зна­чим время пе­ре­да­чи за t. Тогда t₁ = 1/3 t, а t₂ = 2/3 t.

Обо­зна­чим за Q — ко­ли­че­ство дан­ных, q — со­рость пе­ре­да­чи. Пе­ре­ведём Q в Мбиты:

9 000 Мбайт = 72 000 Мбит.

1/3 t * 60 +2/3 t * 90 = 72 000.

t * (20 + 60) = 72 000

От­ку­да на­хо­дим время: t = = 900 с = 15 минут.

Задание 9 № 7 Про­из­во­дит­ся од­но­ка­наль­ная (моно) зву­ко­за­пись с ча­сто­той дис­кре­ти­за­ции 11 кГц и глу­би­ной ко­ди­ро­ва­ния 24 бита. За­пись длит­ся 7 минут, ее ре­зуль­та­ты за­пи­сы­ва­ют­ся в файл, сжа­тие дан­ных не про­из­во­дит­ся. Какое из при­ве­ден­ных ниже чисел наи­бо­лее близ­ко к раз­ме­ру по­лу­чен­но­го файла, вы­ра­жен­но­му в ме­га­бай­тах?

Так как ча­сто­та дис­кре­ти­за­ции 11 кГц, то за одну се­кун­ду за­по­ми­на­ет­ся 11000 зна­че­ний сиг­на­ла.

Глу­би­на ко­ди­ро­ва­ния – 24 бита = 3 байта, время за­пи­си 7 минут = 420 се­кунд, по­это­му для хра­не­ния ин­фор­ма­ции о такой за­пи­си по­тре­бу­ет­ся 11000 * 3 * 420 = 13860000 байт или 13,22 Мб, что близ­ко к 13 Мб.

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Задание 9 № 8
Про­из­во­дит­ся од­но­ка­наль­ная (моно) зву­ко­за­пись с ча­сто­той дис­кре­ти­за­ции 8 кГц и глу­би­ной ко­ди­ро­ва­ния 16 бита. За­пись длит­ся 2 ми­ну­ты, ее ре­зуль­та­ты за­пи­сы­ва­ют­ся в файл, сжа­тие дан­ных не про­из­во­дит­ся. Какое из при­ве­ден­ных ниже чисел наи­бо­лее близ­ко к раз­ме­ру по­лу­чен­но­го файла, вы­ра­жен­но­му в ме­га­бай­тах.

Так как ча­сто­та дис­кре­ти­за­ции 8 кГц, то за одну се­кун­ду за­по­ми­на­ет­ся 8000 зна­че­ний сиг­на­ла.

Глу­би­на ко­ди­ро­ва­ния – 16 бит = 2 байта, время за­пи­си 2 ми­ну­ты = 120 се­кунд, по­это­му для хра­не­ния ин­фор­ма­ции о такой за­пи­си по­тре­бу­ет­ся 8000 * 2 * 120 = 1920000 байт или 1,86 Мб, что близ­ко к 2 Мб.

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Задание 9 № 9
Про­из­во­дит­ся од­но­ка­наль­ная (моно) зву­ко­за­пись с ча­сто­той дис­кре­ти­за­ции 8 кГц и глу­би­ной ко­ди­ро­ва­ния 16 бита. За­пись длит­ся 2 ми­ну­ты, ее ре­зуль­та­ты за­пи­сы­ва­ют­ся в файл, сжа­тие дан­ных не про­из­во­дит­ся. Какое из при­ве­ден­ных ниже чисел наи­бо­лее близ­ко к раз­ме­ру по­лу­чен­но­го файла, вы­ра­жен­но­му в ме­га­бай­тах.

Так как ча­сто­та дис­кре­ти­за­ции 8 кГц, то за одну се­кун­ду за­по­ми­на­ет­ся 8000 зна­че­ний сиг­на­ла.

Глу­би­на ко­ди­ро­ва­ния – 16 бит = 2 байта, время за­пи­си 2 ми­ну­ты = 120 се­кунд, по­это­му для хра­не­ния ин­фор­ма­ции о такой за­пи­си по­тре­бу­ет­ся 8000 * 2 * 120 = 1920000 байт или 1,86 Мб, что близ­ко к 2 Мб.

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Задание 9 № 10
Сколь­ко се­кунд по­тре­бу­ет­ся мо­де­му, пе­ре­да­ю­ще­му со­об­ще­ния со ско­ро­стью 19200 бит/с, чтобы пере­дать цвет­ное раст­ро­вое изоб­ра­же­ние раз­ме­ром пик­се­лей, при усло­вии, что цвет каж­до­го пик­се­ля ко­ди­ру­ет­ся 24 би­та­ми?
По­яс­не­ние.

Время t вы­чис­ля­ет­ся по фор­му­ле t = Q / q, где Q — объем файла, q — cко­рость пе­ре­да­чи дан­ных.

Q = 1280 * 800 * 24 бит = 24 576 000 бит.

t = 24 576 000 бит / 19 200 бит/с = 1280 с.

До­ку­мент объёмом 20 Мбайт можно пе­ре­дать с од­но­го ком­пью­те­ра на дру­гой двумя спо­со­ба­ми. А. Сжать ар­хи­ва­то­ром, пе­ре­дать архив по ка­на­лу связи, рас­па­ко­вать. Б. Пе­ре­дать по ка­на­лу связи без ис­поль­зо­ва­ния ар­хи­ва­то­ра. Какой спо­соб быст­рее и на­сколь­ко, если:

сред­няя ско­рость пе­ре­да­чи дан­ных по ка­на­лу связи со­став­ля­ет 2 23 бит в се­кун­ду;

объём сжа­то­го ар­хи­ва­то­ром до­ку­мен­та равен 50% ис­ход­но­го;

время, тре­бу­е­мое на сжа­тие до­ку­мен­та, — 15 се­кунд, на рас­па­ков­ку — 2 се­кун­ды?

В от­ве­те на­пи­ши­те букву А, если быст­рее спо­соб А, или Б, если быст­рее спо­соб Б. Сразу после буквы на­пи­ши­те число, обо­зна­ча­ю­щее, на сколь­ко се­кунд один спо­соб быст­рее дру­го­го. Так, на­при­мер, если спо­соб Б быст­рее спо­со­ба А на 23 се­кун­ды, в от­ве­те нужно на­пи­сать Б23. Еди­ни­цы из­ме­ре­ния «се­кунд», «сек.», «с.» к от­ве­ту до­бав­лять не нужно.
По­яс­не­ние.

Общее время скла­ды­ва­ет­ся из вре­ме­ни сжа­тия, рас­па­ков­ки и пе­ре­да­чи. Время пе­ре­да­чи t рас­счи­ты­ва­ет­ся по фор­му­ле t = Q / q, где Q — объём ин­фор­ма­ции, q — cко­рость пе­ре­да­чи дан­ных.

Найдём сжа­тый объём: 20 · 0,5 = 10 Мбайт. Пе­ре­ведём Q из Мбайт в биты: 10 Мбай­т = 10 · 2 20 байт = 10 · 2 23 бит. Найдём общее время: t = 15 с + 2 с + 10 · 2 23 бит / 2 23 бит/с = 17 + 10 · 2 0 с = 27 с.

Общее время сов­па­да­ет с вре­ме­нем пе­ре­да­чи: t = 20 · 2 23 бит / 2 23 бит/с = 20 · 2 0 с = 20 с.

Таким об­ра­зом, спо­соб Б быст­рее на 27 − 20 = 7 с.

Про­из­во­дит­ся од­но­ка­наль­ная (моно) зву­ко­за­пись с ча­сто­той дис­кре­ти­за­ции 48 кГц и глу­би­ной ко­ди­ро­ва­ния 16 бит. За­пись длит­ся 2 ми­ну­ты, ее ре­зуль­та­ты за­пи­сы­ва­ют­ся в файл, сжа­тие дан­ных не про­из­во­дит­ся. Какое из при­ве­ден­ных ниже чисел наи­бо­лее близ­ко к раз­ме­ру по­лу­чен­но­го файла, вы­ра­жен­но­му в ме­га­бай­тах?

Так как ча­сто­та дис­кре­ти­за­ции 48 кГц, то за одну се­кун­ду за­по­ми­на­ет­ся 48000 зна­че­ний сиг­на­ла.

Глу­би­на ко­ди­ро­ва­ния – 16 бит = 2 байта, время за­пи­си 2 ми­ну­ты = 120 се­кунд, по­это­му для хра­не­ния ин­фор­ма­ции о такой за­пи­си по­тре­бу­ет­ся 48000 · 2 · 120 = 11520000 байт или 11520000/1024 2 = 10,99 Мб, что близ­ко к 11 Мб.

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Про­из­во­ди­лась двух­ка­наль­ная (сте­рео) зву­ко­за­пись с ча­сто­той дис­кре­ти­за­ции 64 кГц и 24-бит­ным раз­ре­ше­ни­ем. В ре­зуль­та­те был по­лу­чен файл раз­ме­ром 48 Мбайт, сжа­тие дан­ных не про­из­во­ди­лось. Опре­де­ли­те при­бли­зи­тель­но, сколь­ко вре­ме­ни (в ми­ну­тах) про­во­ди­лась за­пись. В ка­че­стве от­ве­та ука­жи­те бли­жай­шее к вре­ме­ни за­пи­си целое число.
По­яс­не­ние.

Так как ча­сто­та дис­кре­ти­за­ции 64 кГц, то за одну се­кун­ду за­по­ми­на­ет­ся 64000 зна­че­ний сиг­на­ла.

Глу­би­на ко­ди­ро­ва­ния 24 бита, т. е. 3 байта. Т. к. за­пись двух­ка­наль­ная, объём па­мя­ти, не­об­хо­ди­мый для хра­не­ния дан­ных од­но­го ка­на­ла, умно­жа­ет­ся на 2, по­это­му, так как по­тре­бо­ва­лось 48 Мбайт, один канал за­ни­ма­ет 24 Мбайт или 24·2 20 байт. Чтобы найти время, в те­че­ние ко­то­ро­го про­во­ди­лась за­пись, не­об­хо­ди­мо раз­де­лить най­ден­ный ин­фор­ма­ци­он­ный объем на глу­би­ну ко­ди­ро­ва­ния и на ча­сто­ту дис­кре­ти­за­ции:

Тем самым, время за­пи­си при­мер­но равно 2 ми­ну­там.

Задание 9 № 14
У Васи есть до­ступ к Ин­тер­нет по вы­со­ко­ско­рост­но­му од­но­сто­рон­не­му ра­дио­ка­на­лу, обес­пе­чи­ва­ю­ще­му ско­рость по­лу­че­ния им ин­фор­ма­ции 2 18 бит в се­кун­ду. У Пети нет ско­рост­но­го до­сту­па в Ин­тер­нет, но есть воз­мож­ность по­лу­чать ин­фор­ма­цию от Васи по низ­ко­ско­рост­но­му те­ле­фон­но­му ка­на­лу со сред­ней ско­ро­стью 2 14 бит в се­кун­ду. Петя до­го­во­рил­ся с Васей, что тот будет ска­чи­вать для него дан­ные объ­е­мом 6 Мбайт по вы­со­ко­ско­рост­но­му ка­на­лу и ре­транс­ли­ро­вать их Пете по низ­ко­ско­рост­но­му ка­на­лу. Ком­пью­тер Васи может на­чать ре­транс­ля­цию дан­ных не рань­ше, чем им будут по­лу­че­ны пер­вые 512 Кбайт этих дан­ных. Каков ми­ни­маль­но воз­мож­ный про­ме­жу­ток вре­ме­ни (в се­кун­дах), с мо­мен­та на­ча­ла ска­чи­ва­ния Васей дан­ных, до пол­но­го их по­лу­че­ния Петей? В от­ве­те ука­жи­те толь­ко число, слово «се­кунд» или букву «с» до­бав­лять не нужно.
По­яс­не­ние.

Нужно опре­де­лить, сколь­ко вре­ме­ни будет пе­ре­да­вать­ся файл объ­е­мом 6 Мбайт по ка­на­лу со ско­ро­стью пе­ре­да­чи дан­ных 2 14 бит/с; к этому вре­ме­ни нужно до­ба­вить за­держ­ку файла у Васи (пока он не по­лу­чит 512 Кбайт дан­ных по ка­на­лу со ско­ро­стью 2 18 бит/с).

Пе­ре­ведём объём ин­фор­ма­ции в Мб в биты: Q = 6 Мб = 6 * 2 20 байт = 6 * 2 23 бит.

Время за­держ­ки: = 512 кб / 2 18 бит/с = 2 (9 + 10 + 3) — 18 c = 2 4 с = 16 c.

Время скчи­ва­ния дан­ных Петей: = 6 * 2 23 бит / 2 14 бит/с = 6 * 2 9 с = 3072 c.

Пол­ное время: = (3072 + 16) c = 3088 c.

Задание 9 № 15
До­ку­мент объёмом 6 Мбайт можно пе­ре­дать с од­но­го ком­пью­те­ра на дру­гой

А. Сжать ар­хи­ва­то­ром, пе­ре­дать архив по ка­на­лу связи, рас­па­ко­вать.

Б. Пе­ре­дать по ка­на­лу связи без ис­поль­зо­ва­ния ар­хи­ва­то­ра.

· ско­рость пе­ре­да­чи дан­ных по ка­на­лу связи со­став­ля­ет 2 22 бит в се­кун­ду;

· объём сжа­то­го ар­хи­ва­то­ром до­ку­мен­та равен 50% от ис­ход­но­го;

· время, тре­бу­е­мое на сжа­тие до­ку­мен­та, — 6 се­кунд, на рас­па­ков­ку — 2 се­кун­ды.

Какой спо­соб быст­рее и на сколь­ко?

В от­ве­те на­пи­ши­те букву А, если быст­рее спо­соб А, или Б, если быст­рее спо­соб Б. Сразу после буквы на­пи­ши­те, на сколь­ко се­кунд один спо­соб быст­рее дру­го­го.

На­при­мер, если спо­соб Б быст­рее спо­со­ба А на 23 се­кун­ды, в от­ве­те нужно на­пи­сать Б23.

Еди­ни­цы из­ме­ре­ния «се­кунд», «сек.», «с» и т. п. к от­ве­ту до­бав­лять не нужно.
По­яс­не­ние.

Общее время скла­ды­ва­ет­ся из вре­ме­ни сжа­тия, рас­па­ков­ки и пе­ре­да­чи. Время пе­ре­да­чи t рас­счи­ты­ва­ет­ся по фор­му­ле t = Q / q, где Q — объём ин­фор­ма­ции, q — cко­рость пе­ре­да­чи дан­ных.

Спо­соб А. Найдём сжа­тый объём: 6 · 0,5 = 3 Мбайт. Пе­ре­ведём Q из Мбайт в биты: 3 Мбай­т = 3 · 2 20 байт = 3 · 2 23 бит. Найдём общее время: t = 6 с + 2 с + 3 · 2 23 бит / 2 22 бит/с = 8 с + 6 с = 14 с.

Спо­соб Б. Общее время сов­па­да­ет с вре­ме­нем пе­ре­да­чи: t = 6 · 2 23 бит / 2 22 бит/с = 12 с.

Таким об­ра­зом, спо­соб Б быст­рее на 14 − 12 = 2 с.

📽️ Видео

Задание 9 | ЕГЭ по информатике | ДЕМО-2024Скачать

Задание 9 // ЕГЭ по информатике 2022Скачать

Демонстрационный вариант егэ по информатике 2022 ФИПИ, задание 9, являться сторонами треугольникаСкачать

Задания 9-10 | ЕГЭ по информатике | ДЕМО-2023Скачать

Очень сложно! Как решать 9 задание в ЕГЭ по информатике l Коля Касперский из ВебиумСкачать

Щелчок 2023 | Задание №9 - Excel (все прототипы)Скачать

Задание 9 // КЕГЭ по информатике 2023Скачать

Задание №9 в EXCEL за 3 минуты | Информатика ЕГЭ — Артем FlashСкачать

Щелчок по информатике - 2023. Электронные таблицы. Задания 3, 9. Информатик БУСкачать

Стрим №2. ЭЛЕКТРОННЫЕ ТАБЛИЦЫ. Задание 9. ЕГЭ по информатике 2023Скачать

Задание 9 // КЕГЭ по информатике 2024Скачать

Задание 9 | ЕГЭ по информатике | ДЕМО-2022Скачать

Решение задания №9. Демоверсия ЕГЭ по информатике - 2023Скачать

Задание №9. Таблицы через Python | Parta 2023 | ИнформатикаСкачать

Решение задания №9. Демоверсия ЕГЭ по информатике - 2022Скачать

Как решать задание №9 Excel | ЕГЭ-2022 по информатике | Кас...Скачать

Задание 9 - 3. DPI. ЕГЭ по информатике.Скачать

Задание 9 ОГЭ 20 информатикаСкачать