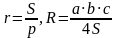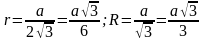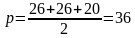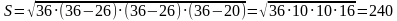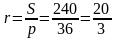Задачи с решениями радиус вписанной окружности

Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.

Площадь треугольника равна произведению его полупериметра (p) на радиус вписанной окружности (r):

Площадь треугольника равна произведению ПЕРИМЕТРА на радиус!

Площадь треугольника равна произведению ПОЛУПЕРИМЕТРА на радиус вписанной окружности

Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.

Из формулы где p — полупериметр, находим, что периметр описанного многоугольника равен отношению удвоенной площади к радиусу вписанной окружности:

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Решение задач по теме «Вписанная и описанная окружности»

Урок №7. СКАЧИВАЙТЕ файл на устройства, чтобы все знаки и формулы были видны и распознаны. Во время чтения файла онлайн происходит потеря формул.

Просмотр содержимого документа
«Решение задач по теме «Вписанная и описанная окружности»»

Тема: Решение задач по теме «Вписанная и описанная окружности»

Задачи: продолжить формирование навыков решения задач по теме.

Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис.

Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров.

Формулы нахождения радиуса вписанной r и описанной R около треугольника окружностей.

Для любого треугольника:

Для равностороннего треугольника.

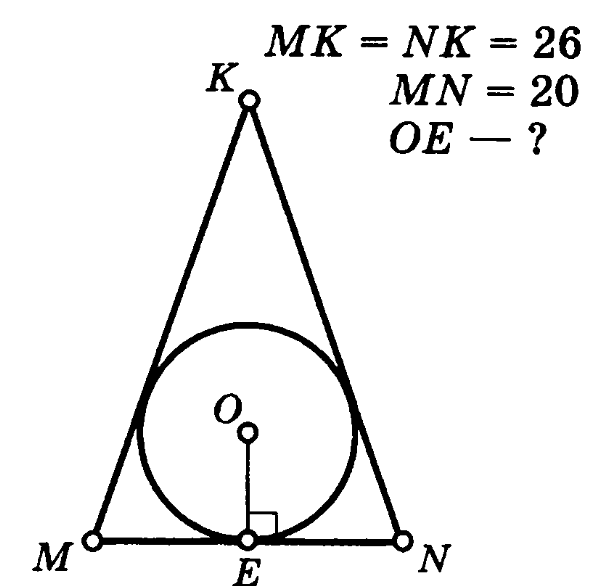
Задача 1. В равнобедренном треугольнике MKN боковые стороны равны 26, а основание – 20. В треугольник вписана окружность с радиусом ОЕ. Найти длину ОЕ.

Решение (краткое). Радиус окружности, вписанной в равнобедренный треугольник можно вычислить по стандартной формуле 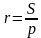, где р – полупериметр.

Ответ: .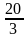

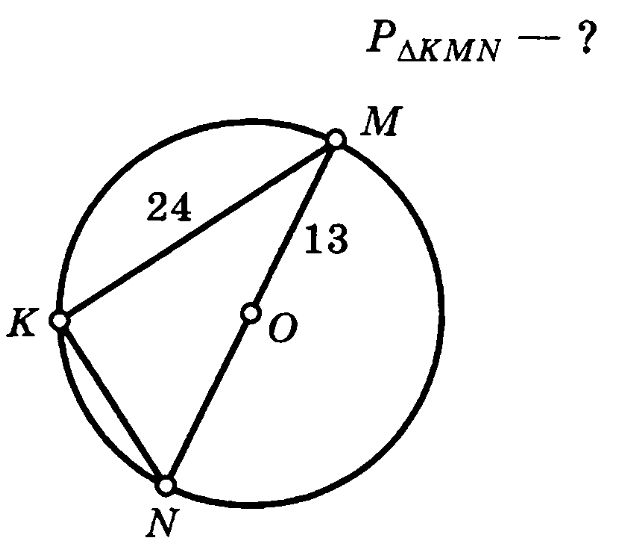
Задача 2. Прямоугольный треугольник KMN описан около окружности радиуса 13. Один из катетов треугольника равен 24. Найти периметр треугольника.

Решение (краткое). MN=d=2r=26, по теореме Пифагора KN=10, Р=60.

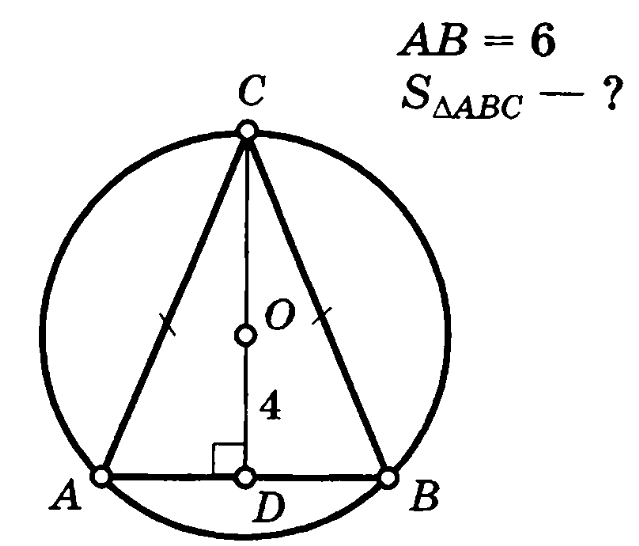
Задача 3. Равнобедренный треугольник АВС вписан в окружность, отрезок ОD=4. Найти площадь треугольника.

Решение (краткое). ОВ=5, ОС=ОВ=5, СD=9, S=0.5*9*6=27.

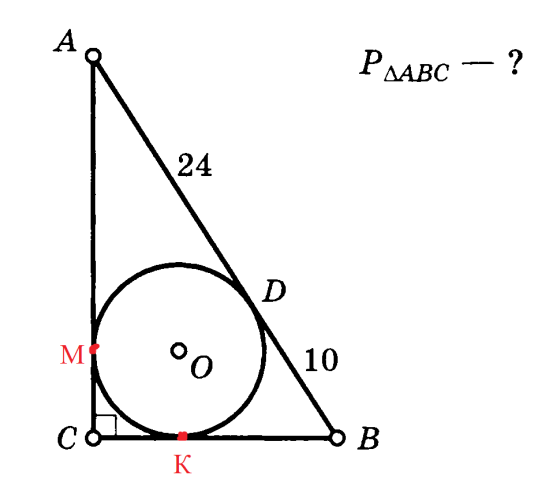
Задача 4. Прямоугольный треугольник описан около окружности. Точка D делит гипотенузу на две части, длинами по 10 и 24. Найти периметр треугольника.

Решение (краткое). DB=DK=10, AD=AM=24.

KOMC – квадрат, т.к. ОК перпендикулярен СВ, ОМ перпендикулярен АС и KC=CM, OK=OM=r.

Пусть KC=CM=х, тогда ВС=10+х, АС=24+х, АВ=24+10=34.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Радиус вписанной окружности, формулы, задачи.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Окружность, вписанная в треугольник

Существование окружности, вписанной в треугольник

Напомним определение биссектрисы угла .

Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.

Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).

Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны , поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,

что и требовалось доказать.

Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла , то она лежит на биссектрисе угла (рис.2).

Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны , поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,

что и требовалось доказать.

Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается сторон этого угла.

Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.

Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).

что и требовалось доказать.

Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных , проведенных к окружности из одной точки, равны.

Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.

Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.

Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).

Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать

r – радиус вписанной окружности, p – полупериметр

.

Посмотреть вывод формулы

a – боковая сторона равнобедренного треугольника , b – основание, r – радиус вписанной окружности

a – сторона равностороннего треугольника, r – радиус вписанной окружности

Посмотреть вывод формул

Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .

Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.

Формулы для радиуса окружности, вписанной в треугольник

Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.

Вывод формул для радиуса окружности, вписанной в треугольник

Теорема 5 . Для произвольного треугольника справедливо равенство

,

где a , b , c – стороны треугольника, r – радиус вписанной окружности, – полупериметр (рис. 6).

что и требовалось.

,

где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).

,

,

то, в случае равнобедренного треугольника, когда

что и требовалось.

где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).

,

то, в случае равностороннего треугольника, когда

что и требовалось.

Замечание . Я рекомендую вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.

Теорема 8 . Для прямоугольного треугольника справедливо равенство

Доказательство . Рассмотрим рисунок 9.

Поскольку четырёхугольник CDOF является прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат . Следовательно,

В силу теоремы 3 справедливы равенства

Следовательно, принимая также во внимание теорему Пифагора , получаем

что и требовалось.

Подборка задач по теме «Окружность, вписанная в треугольник».

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

В треугольнике ABC АС=4, ВС=3, угол C равен 90º. Найдите радиус вписанной окружности.

Катеты равнобедренного прямоугольного треугольника равны 2+. Найдите радиус окружности, вписанной в этот треугольник.

Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу c этого треугольника. В ответе укажите с(–1).

Приведем ряд задач из ЕГЭ с решениями.

. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .

Запишем площадь треугольника АВС двумя способами:

Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .

В ответ запишем .

Ответ: .

1. В произвольном две боковые стороны 10см и 6см (AB и BC). Найти радиусы описанной и вписанной окружностей
Задача решается самостоятельно с комментированием.

Решение:

В .

1) Найти:
2) Доказать: и найти СK
3) Найти: радиусы описанной и вписанной окружностей

Р адиус окружности вписанной в квадрат равен . Найти радиус окружности описанной около этого квадрата.
Дано :

треугольник ОСЕ – равнобедренный и прямоугольный;

ОЕ=ЕС=;

Найти: ОС=?
Решение: в данном случае задачу можно решить, воспользовавшись либо теоремой Пифагора, либо формулой для R. Второй случай будет проще, поскольку формула для R выведена из теоремы.

Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу с этого треугольника. В ответе укажите .

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S – площадь треугольника

Нам неизвестны ни стороны треугольника, ни его площадь. Обозначим катеты как х, тогда гипотенуза будет равна:

А площадь треугольника будет равна 0,5х 2 .

Таким образом, гипотенуза будет равна:

В ответе требуется записать:

В треугольнике ABC АС = 4, ВС = 3, угол C равен 90 0 . Найдите радиус вписанной окружности.

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S – площадь треугольника

Две стороны известны (это катеты), можем вычислить третью (гипотенузу), также можем вычислить и площадь.

По теореме Пифагора:

Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S – площадь треугольника

Известны все стороны, вычислим и площадь. Её мы можем найти по формуле Герона:

Задача 10. (Из банка ЕГЭ)

Задача 11. (Из банка ЕГЭ)

Задача 12. (Из банка ЕГЭ)

Задача 13. (Из банка ЕГЭ)

Задача 14. (Из банка ЕГЭ)

Найдите радиусы окружностей, вписанной в правильный треугольник и описанный около него, если их разность равна 4см.

Сторона правильного треугольника вычисляется по формуле a = R √3 , где R – радиус описанной окружности, и a = 2r √3 , где r – радиус вписанной окружности, приравняем стороны R √3 = 2·r √3 , отсюда R = 2r, сдругой сторони по условию задачи R – r = 4 cм, отсюда r = 4 см, тогда R = 2·4 см = 8 см

Ответ: 4 см, 8 см

Задача 16.
Катеты прямоугольного треугольника равны 12 и 5. Найти:
а) радиусы вписанной окружности;
б) радиусы описанной окружности;
в) расстояние от центра вписанной окружности до вершины наименьшего угла.
Решение:
1. По теореме Пифагора
2. О – центр описанной окружности,

В треугольнике с углами и вписана окружность. Найти углы треугольника, вершинами которого являются точки касания окружности со сторонами треугольника.

Дано: точки касания вписанной окружности.

Найти:

Решение:

1.

2. Из

3. Из

4. Из

5.

В равнобедренную трапецию с основаниями 1 и 9 вписана окружность. Найти: а) боковую сторону; б) радиус вписанной окружности; в) высоту; г) диагональ.

Приведу пример возможной самостоятельной работы по теме «Вписанная и описанная окружность».

Карточки с задачами.
1) В ABC AB = 8, BC = 10, . Найти высоту, опущенную из вершины B и BAC.
2) В ABC AB=12 , BC = 9. Площадь треугольника 9 . Найти радиусы вписанной и описанной окружностей.

Пример математического диктанта.

I. Математический диктант
I вариант
1. В любой треугольник можно вписать окружность? (Да/Нет)
2. Центр вписанной в треугольник окружности является …
3. Вокруг любого треугольника можно описать окружность? (Да/Нет)
4. Центр окружности описанной около треугольника является …
5. Если центр вписанной и описанной окружности совпадают, то это треугольник …
6. Центр окружности, описанной около прямоугольного треугольника, совпадает с …
7. Если в трапецию можно вписать окружность, то …
8. Если вокруг трапеции можно описать окружность, то …
9. Если центр окружности, описанной около треугольника находится вне его, то этот треугольник …
10. Если центр окружности, описанной около треугольника, находится внутри его, то треугольник …
Использовать взаимопроверку, заготовить заранее ответы на доске. Анализ ошибок.

📸 Видео

Формулы для радиуса окружности #shortsСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Геометрия 9 класс. Вписанные и описанные окружности. Ключевая задача № 4.Скачать

Радиус описанной окружностиСкачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Математика за минуту: Объяснение формулы радиуса вписанной окружности в прямоугольный треугольник.Скачать

Задача № 27933 ЕГЭ по математике. Урок 147Скачать

Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать