В данной публикации мы рассмотрим основные свойства высоты равнобедренного треугольника, а также разберем примеры решения задач по данной теме.
Примечание: треугольник называется равнобедренным, если две его стороны равны (боковые). Третья сторона называется основанием.
- Свойства высоты в равнобедренном треугольнике
- Свойство 1
- Свойство 2
- Свойство 3
- Пример задачи
- Задачи равнобедренный треугольник высота
- Свойства и признаки равнобедренного треугольника
- ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ:
- Теоретический тест с последующей самопроверкой
- Задачи равнобедренный треугольник высота
- Контакты
- 📸 Видео
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Свойства высоты в равнобедренном треугольнике
Свойство 1
В равнобедренном треугольнике две высоты, проведенные к боковым сторонам, равны.
Обратная формулировка: Если в треугольнике две высоты равны, значит он является равнобедренным.
Свойство 2
В равнобедренном треугольнике высота, опущенная на основание, одновременно является и биссектрисой, и медианой, и серединным перпендикуляром.
- BD – высота, проведенная к основанию AC;
- BD – медиана, следовательно, AD = DC;
- BD – биссектриса, следовательно, угол α равен углу β.
- BD – серединный перпендикуляр к стороне AC.
Свойство 3
Если известны стороны/углы равнобедренного треугольника, то:
1. Длина высоты ha, опущенной на основание a, вычисляется по формуле:
2. Длина высоты hb, проведенной к боковой стороне b, равняется:
p – это полупериметр треугольника, рассчитывается таким образом:
3. Высоту к боковой стороне можно найти через синус угла и длину стороны треугольника:
Примечание: к равнобедренному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.
Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Пример задачи
Задача 1
Дан равнобедренный треугольник, основание которого равно 15 см, а боковая сторона – 12 см. Найдите длину высоты, опущенной к основанию.
Решение
Воспользуемся первой формулой, представленной в Свойстве 3:
Задача 2
Найдите высоту, проведенную к боковой стороне равнобедренного треугольника длиной 13 см. Основание фигуры равняется 10 см.
Решение
Для начала вычислим полупериметр треугольника:
Теперь применим соответствующую формулу для нахождения высоты (представлена в Свойстве 3):
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Задачи равнобедренный треугольник высота
Равнобедренный треугольник — треугольнику которого две стороны равны.
Равные стороны называют боковыми сторонами, а третью сторону — основанием.
Свойства равнобедренного треугольника были известны с давних времен. Еще древние вавилоняне (II в. до н.э.) знали, что углы у основания равнобедренного треугольника равны. Любой треугольник можно разрезать на равнобедренные треугольники.
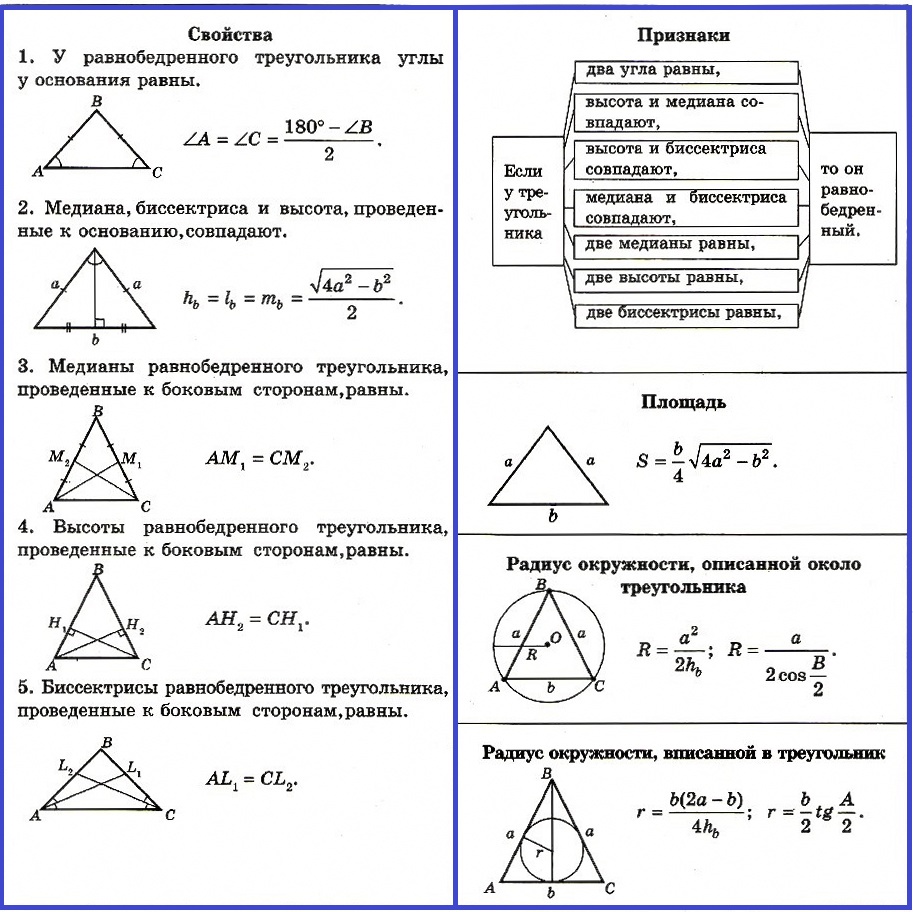
Свойства и признаки равнобедренного треугольника
Свойства равнобедренного треугольника:
1. У равнобедренного треугольника углы у основания равны (теорема).
2. Медиана, биссектриса и высота, проведенные к основанию, совпадают (теорема).
3. Медианы равнобедренного треугольника, проведенные к боковым сторонам, равны.
4. Высоты равнобедренного треугольника, проведенные к боковым сторонам, равны.
5. Биссектрисы равнобедренного треугольника, проведенные к боковым сторонам, равны.
Признаки равнобедренного треугольника:
Если у треугольника есть один из нижеуказанных признаков, то он равнобедренный:
— два угла равны,
— высота и медиана совпадают,
— высота и биссектриса совпадают,
— медиана и биссектриса совпадают,
— две медианы равны,
— две высоты равны,
— две биссектрисы равны.
ПРИМЕРЫ РЕШЕНИЯ
КЛЮЧЕВЫХ ЗАДАЧ:
Задача № 1. Дано: ΔABC — равносторонний, ΔADC — равнобедренный (AD=CD), AC — общая сторона, BC = 8 см, PADC > PABC в 1,5 раза. Найти: CD.
Задача № 2. Дано: ΔABC — равнобедренный, AB = BC, AD — медиана, AB + BD = 27 см, AC + CD = 21 см. Найти: AB, BC, AC.
Задача № 3. Дано: ΔABC — равнобедренный, AB = BC, ∠1 = 130°. Найти: ∠2.
Теоретический тест
с последующей самопроверкой
- Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно. - Если треугольник равносторонний, то:
а) он равнобедренный;
б) все его углы равны;
в) любая его высота является биссектрисой и медианой. - В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем. - Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно. - Если треугольник равнобедренный, то:
а) он равносторонний;
б) любая его медиана является биссектрисой и высотой;
в) два его угла равны. - В каком треугольнике любая его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем. - Если в треугольнике два угла равны, то этот треугольник является:
а) равносторонним;
б) равнобедренным;
в) прямоугольным. - Если в треугольнике две стороны равны, то:
а) у него равны два угла;
б) у него все углы равны;
в) этот треугольник равносторонний.
- Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение: б) может быть верно.
- Если треугольник равносторонний, то: а) он равнобедренный; б) все его углы равны; в) любая его высота является биссектрисой и медианой.
- В каком треугольнике только одна его высота делит треугольник на два равных треугольника? б) в равнобедренном.
- Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение: а) всегда верно.
- Если треугольник равнобедренный, то: в) два его угла равны.
- В каком треугольнике любая его высота делит треугольник на два равных треугольника? в) в равностороннем.
- Если в треугольнике два угла равны, то этот треугольник является: б) равнобедренным.
- Если в треугольнике две стороны равны, то: а) у него равны два угла.
Вы смотрели конспект по теме «Равнобедренный треугольник + ЗАДАЧИ по теме». Выберите дальнейшие действия:
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Задачи равнобедренный треугольник высота
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |