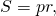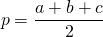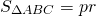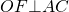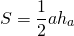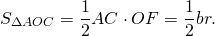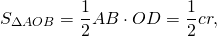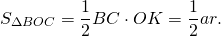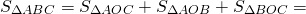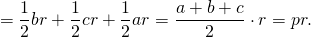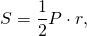Класс: 10
- Презентация к уроку
- I. Организационная часть:
- II. Повторение материала, решение задач, знакомство с новыми формулами.
- III. Домашнее задание. Приложение 2.
- IV. Итог урока.
- Площадь треугольника через радиус вписанной окружности
- 2 Comments
- Как найти площадь треугольника
- По формуле Герона
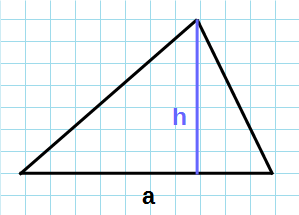
- Через основание и высоту
- Через две стороны и угол
- Через сторону и два прилежащих угла
- Площадь прямоугольного треугольника
- Площадь равнобедренного треугольника через стороны
- Площадь равнобедренного треугольника через основание и угол
- Площадь равностороннего треугольника через стороны
- Площадь равностороннего треугольника через высоту
- Площадь равностороннего треугольника через радиус вписанной окружности
- Площадь равностороннего треугольника через радиус описанной окружности
- Площадь треугольника через радиус описанной окружности и три стороны
- Площадь треугольника через радиус вписанной окружности и три стороны
- 💡 Видео
Презентация к уроку
Цель урока:
- Образовательная цель: обеспечить в ходе урока сознательное повторение формул для вычисления площади треугольника, которые изучаются в школьной программе. Показать необходимость знания II формулы Герона, формулы площади треугольника, заданного в прямоугольной системе координат. Обеспечить сознательное усвоение и применение этих формул при решении задач. Показать формулу площади треугольника через радиусы вписанной и вневписанных окружностей. Учиться получать следствия из формул и показать это на некоторых выводах.
- Воспитательная цель: воспитывать сознательное отношение к учебе повышение интереса к математике, к истории математики, к научно-исследовательской работе.
- Развивающая цель: развивать логическое мышление, математическую речь. умение сравнивать и делать выводы; совершенствовать навыки работы с формулами, учиться получать из них следствия.
Методы и приёмы: словесный и наглядный.
По типу: урок обобщения и систематизации знаний.
Наглядность к уроку и раздаточный материал:
- презентация;
- памятки с рисунками, где учащиеся будут записывать формулы (приложение 1);
- задания для практической работы (приложение 2);
- учебник.
Ход урока
I. Организационная часть:
- Приветствие.
- Подготовка учащихся к уроку.
- Получение сведений об отсутствующих.
II. Повторение материала, решение задач, знакомство с новыми формулами.
Сегодня у нас обобщающий урок повторения по теме «Формулы для вычисления площадей различных треугольников». Зная формулы для вычисления площади треугольника, можно посчитать площадь любого многоугольника, предварительно разбив его на треугольники. Эта тема является одной из важнейших тем геометрии.
Мы повторим те формулы, которые вы знаете. Я вам покажу ещё несколько формул, знать которые необходимо для успешной сдачи ЕГЭ. И применим эти формулы при решении задач.
Запишите тему урока. Прежде чем приступить непосредственно к формулам давайте вспомним две теоремы геометрии, которые используются при их доказательствах — это теорема синусов и теорема косинусов.
1. 


2. 

Напишите эту формулу для a 2 , b 2 .
Какие же формулы для вычисления площади треугольника вы знаете?
Площадь прямоугольного треугольника. S=
Площадь любого треугольника. S= 




Слайд 4. Площадь треугольника по двум сторонам и углу между ними.
S=½·ab·sinα. Запишите формулу (приложение 1).
Площадь треугольника через радиус вписанной окружности. S = 
Здесь уместно вспомнить, как строится вписанная окружность. Запишите формулу (приложение 1).
Площадь треугольника через R-радиус описанной окружности.

Здесь также можно вспомнить, как строится описанная окружность.
I Формула Герона.
S =
Доказательство первой формулы Герона. Запишите формулу (приложение 1).
Формула площади треугольника по трём сторонам была открыта Архимедом в III в до н.э. Однако соответствующая работа до наших дней не дошла. Эта формула содержится в «Метрике» Герона Александрийского (I в н. э.) и названа в его честь. Герон интересовался треугольниками с целочисленными сторонами, площади которых также являются целыми. Такие треугольники носят название героновых треугольников. Простейшим Героновым треугольником является египетский треугольник
Как посчитать площадь треугольника. если хотя бы одна сторона выражена квадратным корнем? II Формула Герона. Применяя предыдущую формулу, получим следующую.
S= 
Её называют II формулой Герона. И если стороны треугольника а,b,с , то записать ее можно в виде:
S=
Запишите формулу (приложение 1) (см. учебник Атанасяна Л. С. «Геометрия 10-11», 2010 год, стр. 200).
Рассмотрим решение задачи на применение этой формулы.
А вот при решении следующей задачи нам необходимо вспомнить формулы нахождения медиан треугольника. Запишите формулы (приложение 1).
Формулы медиан треугольника (см. учебник Атанасяна Л. С. «Геометрия 10-11», 2010 год, стр. 195).
ma= 
mb=
mc= 
Давайте решим одну замечательную задачу на применение данных формул. (Условие задачи с рисунком на листочках выдаётся каждому ученику. Здесь же они пишут решение. Каждый пункт решения проверяется с использованием слайда). Приложение 2.
А как посчитать площадь треугольника в системе координат? Рассмотрим это на примере. Можно вычислить стороны треугольника, а затем его площадь по II формулой Герона. Но здесь громоздкие вычисления и без калькулятора не обойтись. А нет ли ещё какой-нибудь формулы для вычисления площади треугольника?
Такая формула существует. S= 
Доказательство этой формулы очень громоздкое и мы не будем на нём подробно останавливаться. Если оно вас заинтересует, то можно разобрать его после урока.
Давайте попробуем применить эту формулу при решении задачи, текст которой у вас на тех же листочках. (Приложение 2).
Задача: А(0;0), В(5:7), С(4:-2). Найти площадь треугольника. Отв.19.
Итак, теперь мы знаем 8 формул для нахождения площади треугольника.
Но оказывается это не все формулы.
Существуют ещё формулы и следствия из предыдущих формул.
Вычисление площади треугольника по стороне и прилежащим к ней углам.

Вычисление площади треугольника по стороне и прилежащим к ней углам. Эту формулу можно получить из предыдущей, используя тригонометрическую формулу синуса суммы.
Вычисление площади треугольника через все углы и радиус описанной окружности.

Вычисление площади треугольника через все углы и одну из сторон треугольника.

Вычисление площади треугольника через радиусы вневписанных окружностей. Эту формулу не используют в школе. Но в материалах группы С ЕГЭ встречаются задачи, где можно быстро найти ответ, применив эту формулу.
Итак, мы теперь знаем 13 формул. Но это ещё не предел. С таким же успехом можно получить ещё новые формулы, например, через тригонометрические формулы половинного угла, двойного угла. Такие исследования могут стать стартовой площадкой для написания научно-исследовательской работы.
Слайд 24.
Интернет-ресурсы. На этом слайде вы видите сайт, где есть программа вычисления площадей треугольников по первым семи формулам для самых ленивых. Недостаток этой программы в том, что считает она приближённо в десятичных дробях.
III. Домашнее задание. Приложение 2.
1. А(2;3), В(5:-4), С(-1;-3). Найти площадь треугольника АВС.
2. В ∆АВС a=6, b = 

4) R (радиус описанной окружности).
IV. Итог урока.
Объявить оценки за работу на уроке.
Какие формулы вы сегодня повторили?
Какие формулы вы узнали только сегодня?
Те листочки, на которых вы записали формулы, пусть послужат вам справочным материалом при решении задач на уроке, дома и при подготовке к ЕГЭ.
Видео:112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Площадь треугольника через радиус вписанной окружности
Как найти площадь треугольника через радиус вписанной окружности?
Площадь треугольника равна произведению радиуса вписанной в этот треугольник окружности на на его полупериметр.
Формула для нахождения площади треугольника через радиус вписанной окружности:
окружность (O; r) — вписанная,
Рассмотрим треугольник AOC.
(как радиус, проведенный в точку касания).
Следовательно, OF — высота треугольника AOC.
Так как площадь треугольника ABC равна сумме площадей этих треугольников, то
Что и требовалось доказать.
Если требуется найти площадь треугольника через его периметр, формулу записывают так:
где P — периметр треугольника, r — радиус вписанной в этот треугольник окружности.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

2 Comments
Полезно, вспомнить курс школьной геометрии.
Разработчики сайта дерзайте дальше.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
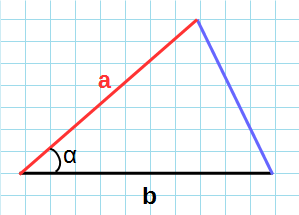
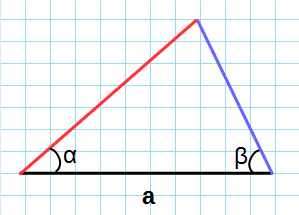
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
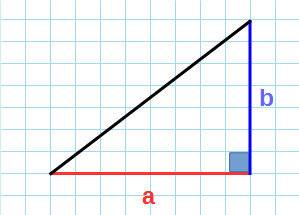
Площадь прямоугольного треугольника
Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
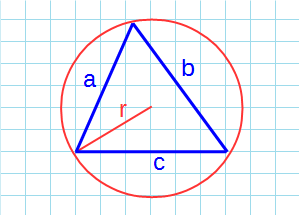
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
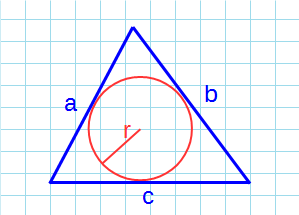
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
💡 Видео
Вычисление площади треугольника через радиусы вписанной и описанной окружностей.Скачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Формула радиуса вписанной окружности треугольника. Геометрия 9 классСкачать

Задание 24 Площадь описанного треугольникаСкачать

площадь треугольника. радиус вписанной окружностиСкачать

9 класс, 12 урок, Теорема о площади треугольникаСкачать

Формулы площади треугольника. Вписаная и описаная окружностьСкачать

Геометрия 8. Урок 14 - Площадь треугольников. Формулы и задачи.Скачать

Геометрия Доказательство Площадь треугольника равна произведению его полупериметра и радиусаСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

ОГЭ Задание 26 Треугольник Вписанная окружность ПлощадьСкачать

Радиус вписанной окружности, формулу через площадь и полупериметрСкачать

ОГЭ, задание 23 (геометрическая задача на вычисление). Треугольники, часть 2Скачать