Задачи на углы и отрезки связанные с окружностью 10 класс

Просмотр содержимого документа
«Углы и отрезки, связанные с окружностью»

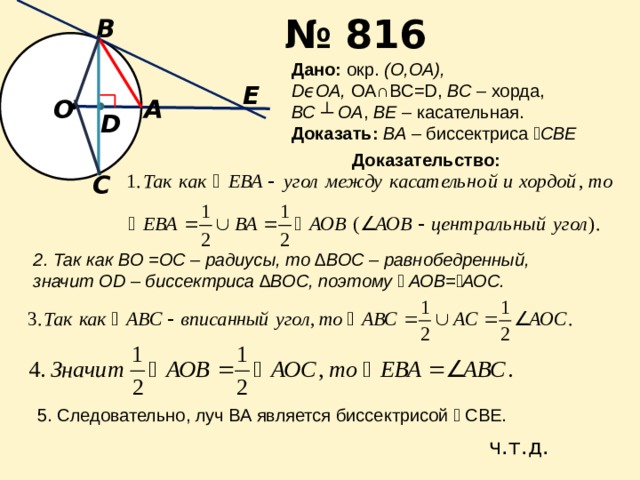
Углы и отрезки, связанные с окружностью

ВС ┴ ОА , ВЕ – касательная.

2. Так как ВО =ОС – радиусы, то ∆ВОС – равнобедренный,

значит OD – биссектриса ∆ВОС, поэтому ے АОВ= ے АОС.

5. Следовательно, луч ВА является биссектрисой ے СВЕ.

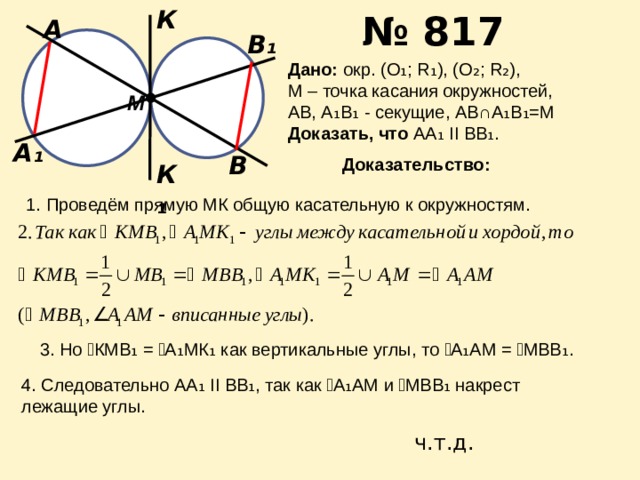
М – точка касания окружностей,

АВ, А₁В₁ — секущие, АВ∩А₁В₁=М

Доказать, что АА₁ II ВВ₁.

1. Проведём прямую МК общую касательную к окружностям.

3. Но ے КМВ₁ = ے А₁МК₁ как вертикальные углы, то ے А₁АМ = ے МВВ₁.

4. Следовательно АА₁ II ВВ₁, так как ے А₁АМ и ے МВВ₁ накрест

Дано: АС – касательная к окр. (О₁; R₁), BD – касательная к окр. (О₂; R₂)

Доказать, что а) AD II BC; б) AB² = AD · BC; в) BD² : AC² = AD : BC.

б) 3) ∆ABD ̴ ∆ABC по I признаку подобия треугольников, то

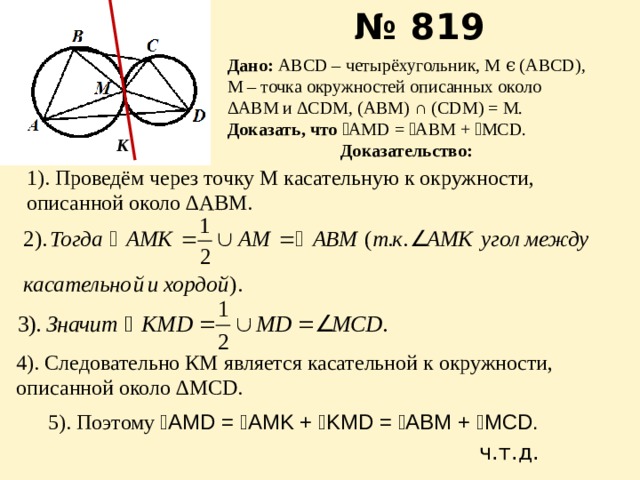
Дано: ABCD – четырёхугольник, М ϵ (ABCD),

М – точка окружностей описанных около

∆ АВМ и ∆CDM, (ABM) ∩ (CDM) = M.

Доказать, что ے AMD = ے ABM + ے MCD.

1). Проведём через точку М касательную к окружности, описанной около ∆АВМ.

4). Следовательно КМ является касательной к окружности, описанной около ∆MCD.

5). Поэтому ے AMD = ے AMK + ے KMD = ے ABM + ے MCD.

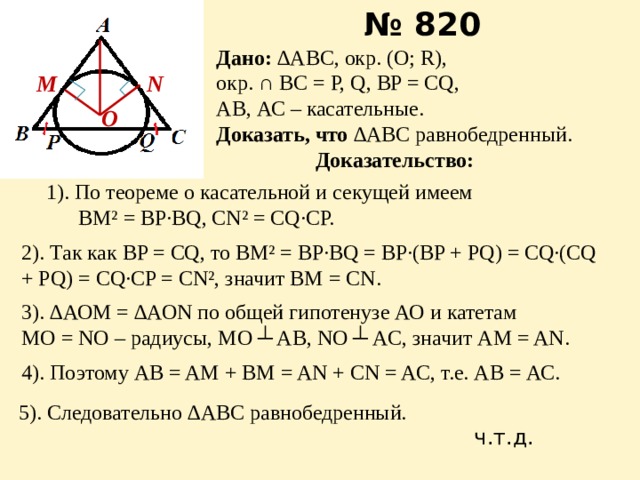
окр. ∩ BC = P, Q, BP = CQ,

АВ, АС – касательные.

Доказать, что ∆АВС равнобедренный.

1). По теореме о касательной и секущей имеем

ВМ² = ВР·BQ, CN² = CQ·CP.

2). Так как BP = CQ, то BM² = BP·BQ = BP·(BP + PQ) = CQ·(CQ + PQ) = CQ·CP = CN², значит ВМ = СN.

3). ∆АОМ = ∆АОN по общей гипотенузе АО и катетам

MO = NO – радиусы, MO ┴ AB, NO ┴ AC, значит AM = AN.

4). Поэтому AB = AM + BM = AN + CN = AC, т.е. АВ = АС.

5). Следовательно ∆АВС равнобедренный.

Дано: окр. (О; R), AB ∩ CD = E,

Доказать, что EC = EB или EC = EA, ED = EB или ED = EA.

1). По теореме о пересечения хорд имеем AE · EB = CE · DE.

2). Так как хорды AB = CD, то выразим DE через AB,

DE = AE + EB – CE, AE · EB = CE · (AE + EB – CE),

AE·EB = CE·AE + CE·EB – CE²,

AE·EB – CE·AE – CE·EB + CE² = 0,

AE·(EB – CE) – CE·(EB – CE) = 0, (EB – CE)·(AE – CE) = 0.

3). Значит либо EB – CE = 0 или либо AE – CE = 0.

4). Следовательно EB = CE или AE = CE, тогда EB = ED или EA = ED.

Дано: окр. (О; R), КА – хорда,

КВ – касательная, ОN ﬩ OA,

ON ∩ KA = M, OM ∩ KB = N.

Доказать, что NK = NM.

1). Так как ОК- радиус, КВ – касательная, то ОК ﬩ КВ и КА ∩ ON = M, значит ے NKM = 90 ° — ے AKO.

2). ∆АОМ – равнобедренный (ОА = ОК – радиусы), то ے ОКА = ے ОАК.

3). ∆АОМ, ے АОМ = 90 °, (ON ﬩ OA) , то ے АМО = 90 ° – ے МАО.

4). Значит ے NKM = ے AMO.

5). Но ے АМО = ے NMK как вертикальные углы, значит ے NKM = ے NMK.

6). Следовательно ∆KMN равнобедренный, а значит NK = NM.

Дано: окр. (О; R), АВ, АС, В ₁ С ₁ — хорды, АВ ∩ В ₁ С ₁ = М,

АС ∩ В ₁ С ₁ = N, ᴗАВ ₁ = ᴗ В ₁ В, ᴗ АС ₁ = ᴗ С ₁ С.

Доказать, что AM =AN.

2). Но ᴗАВ ₁ = ᴗ В ₁ В и ᴗ АС ₁ = ᴗ С ₁ С, значит ے АМС ₁ = ے ANB ₁ .

3). Следовательно ∆AMN равнобедренный, поэтому AM =AN.

Дано: окр. (О; R), А, В, С, D ϵ окр.,

ВМ – биссектриса ∆АВС, ВМ ϵ BD.

Доказать, что ے AMD = ے BAD.

1). Так как ВМ – биссектриса ∆АВС, то ے АВМ = ے МВС.

2). Так как вписанные углы ے DBC и ے DAC опираются на одну и ту же ᴗ СD, то ے DВC = ے DAС.

3). Следовательно ے АВМ = ے МВС = ے DAС.

4). Из теоремы о сумме углов ∆АMD и ∆ABD, имеем ے AMD = 180 ° — ے DAМ – ے МDA, ے BAD = 180 ° –

– ے ABD – ے BDA, т.е. ے BAD = 180 ° – ے DAM – ے MDA.

5). Следовательно ے AMD = ے BAD.

Дано: ∆АВС, АА ₁ , ВВ ₁ – высоты.

Доказать, что А, В, А ₁ , В ₁ ϵ окр. (О; R).

1). Возьмем точку К ϵ АВ, так что АК = КВ.

2). Так как ∆АВВ ₁ , ے В ₁ = 90 ° , то КВ ₁ = КА = КВ.

3). Так как у прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы, т.е. в точке К, то точки А, В, В ₁ ϵ окр. (К; КВ ₁).

4). Так как ∆АВА₁, ے А ₁ = 90 ° , то КА ₁ = КА = КВ.

5). Значит точки А, В, А ₁ ϵ окр. (К; КА ₁).

6). Следовательно точки А, В, А ₁ , В ₁ ϵ окр. (К; КВ ).

Дано: АВСD – вписанный четырёхугольник, АС ﬩ ВD – диагонали.

Доказать, что AB² + CD² = BC² + AD² = d².

1). Обозначим ے CAD = φ, тогда ے ADB = 90° – φ.

3). Выразим и сложим АВ = 2Rcos φ , CD = 2Rsin φ, тогда AB² + CD² = 4R².

4). По теореме Пифагора из треугольников имеем AB² + CD² = (BK² + AK²) + (CK² + DK²) = (BK² + CK²) + (AK² + DK²) = BC² + AD² = 4R² = d².

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Самостоятельная работа по геометрии «Углы и отрезки, связанные с окружностью» (10 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Тема: «Углы и отрезки, связанные с окружностью».

№ 1. Угол ACB вписан в окружность. Градусные величины дуг AC и BC равны и соответственно. Найдите угол ACB.

№ 2. Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.

№ 3. Углы ABC и BCD вписаны в окружность и равны и соответственно, S – точка пересечения прямых AB и CD. Найдите угол ASC

№ 4. АВ и ВС – отрезки касательных, проведенных к окружности с центром О радиуса 10 см. Найдите периметр четырёхугольника АВСО, если угол АОС равен .

№ 5. Угол между диаметром АВ и хордой АС равен . Через точку С проведена касательная, пересекающая прямую АВ в точке Е. Найдите СЕ, если радиус окружности равен 6 см.

Тема: «Углы и отрезки, связанные с окружностью».

№ 1. Угол ACB вписан в окружность. Градусные величины дуг AC и BC равны и соответственно. Найдите угол ACB.

№ 2. Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 6:13:17. Найдите радиус окружности, если меньшая из сторон равна 18.

№ 3. Углы ABC и BCD вписаны в окружность и равны и соответственно, S – точка пересечения прямых AB и CD. Найдите угол ASC

№ 4. АВ и ВС – отрезки касательных, проведенных к окружности с центром О радиуса 6 см. Найдите периметр четырёхугольника АВСО, если угол АВС равен .

№ 5. Угол между диаметром АВ и хордой АС равен . Через точку С проведена касательная, пересекающая прямую АВ в точке К. Найдите радиус окружности, если СК= 4 см.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 988 человек из 78 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 672 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Геометрия. Углы и отрезки, связанные с окружностью.Скачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 540 713 материалов в базе

Материал подходит для УМК

«Геометрия. Учебник 10-11 класс », Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.

§ 1. Углы и отрезки, связанные с окружностью

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 18.08.2020
• 264
• 7

• 16.08.2020
• 7698
• 215

• 16.08.2020
• 301
• 12

• 15.08.2020
• 421
• 16

• 14.08.2020
• 127
• 1

• 14.08.2020
• 1241
• 118

• 13.08.2020
• 477
• 25

• 13.08.2020
• 231
• 19

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 19.08.2020 2451
• DOCX 27.6 кбайт
• 338 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Беляевская Светлана Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 6 месяцев
• Подписчики: 0
• Всего просмотров: 12951
• Всего материалов: 18

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Калужской области школьники уйдут на каникулы с 7 по 20 февраля

Время чтения: 1 минута

Минобороны начало вакцинацию подростков от COVID-19

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

У детей на портале госуслуг появятся собственные аккаунты

Время чтения: 1 минута

Петербургских школьников с 7 по 11 классы перевели на дистанционное обучение

Время чтения: 1 минута

Онлайн-семинар о развитии управляющих функций мозга ребенка

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Алгебра 10 класс (Урок№29 - Радианная мера угла.)Скачать

Углы и отрезки, связанные с окружностью.
презентация к уроку по геометрии (10 класс) на тему

Первый урок по геометрии в 10 классе по теме «Некоторые сведения из планиметрии».

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Скачать:

Видео:Углы, связанные с окружностьюСкачать

Предварительный просмотр:

Аннатация к презентации урока № 1

1. Устная работа. Слайды № 4 — № 8

1. Что такое радиус?
2. Что такое диаметр?
3. Что такое хорда?
4. Что такое касательная?
5. Что такое секущая?
6. Что такое дуга?
7. Какой угол называется центральным углом окружности?
8. Какой угол называется вписанным?
9. Сформулировать теорему о центральном угле.
10. Сформулировать теорему о вписанном угле.

1. Изучение нового материала. Слайды № 9 — № 15

1. Угол между касательной и хордой.
2. Две теоремы об отрезках, связанных с окружностью.
3. Углы с вершинами внутри и вне круга.

1. Закрепление нового материала. Слайды № 16 — № 21.

1. Решение задач по готовым чертежам. Слайды № 16 — № 20.

Действия ученика: решая задачу с места комментируя каждый шаг действия и оформляя задачи в тетрадь.

Действия учителя: проверять комментарии ученика и находить и исправлять ошибки совместно с учеником.

1. Решение задач по учебнику. Слайд № 21.

Действия ученика: один ученик решает задачу у доски под присмотром учителя, а остальные в тетради.

Действия учителя: проверять записи находить и исправлять ошибки.

Ученик отвечает с места.

1. Домашнее задание. Слайд № 23.

📺 Видео

10 класс, 11 урок, Числовая окружностьСкачать

11 класс, 41 урок, Две теоремы об отрезках, связанных с окружностьюСкачать

Синус, косинус произвольного угла. 9 класс.Скачать

Смирнов В.А. Углы и отрезки, связанные с окружностьюСкачать

Углы, связанные с окружностьюСкачать

Урок 10. Углы и отрезки, связанные с окружностью.Скачать

Урок1. Углы и отрезки, связанные с окружностью.Скачать

Угол между прямыми в пространстве. 10 класс.Скачать

Урок 2. Углы и отрезки, связанные с окружностью.Скачать

Пропорциональные отрезки в окружности. Практическая часть. 9 класс.Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Длина окружности. Площадь круга. 6 класс.Скачать

Углы, вписанные в окружность. 9 класс.Скачать

Окружность и все, что с ней связано | Математика 10 класс | УмскулСкачать