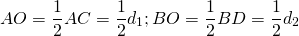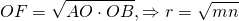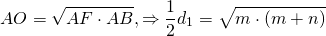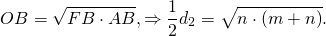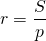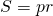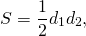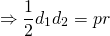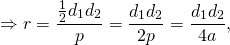Задачи на ромб и вписан в него окружности

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Задачи на ромб и окружность

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Задачи на ромб и окружность

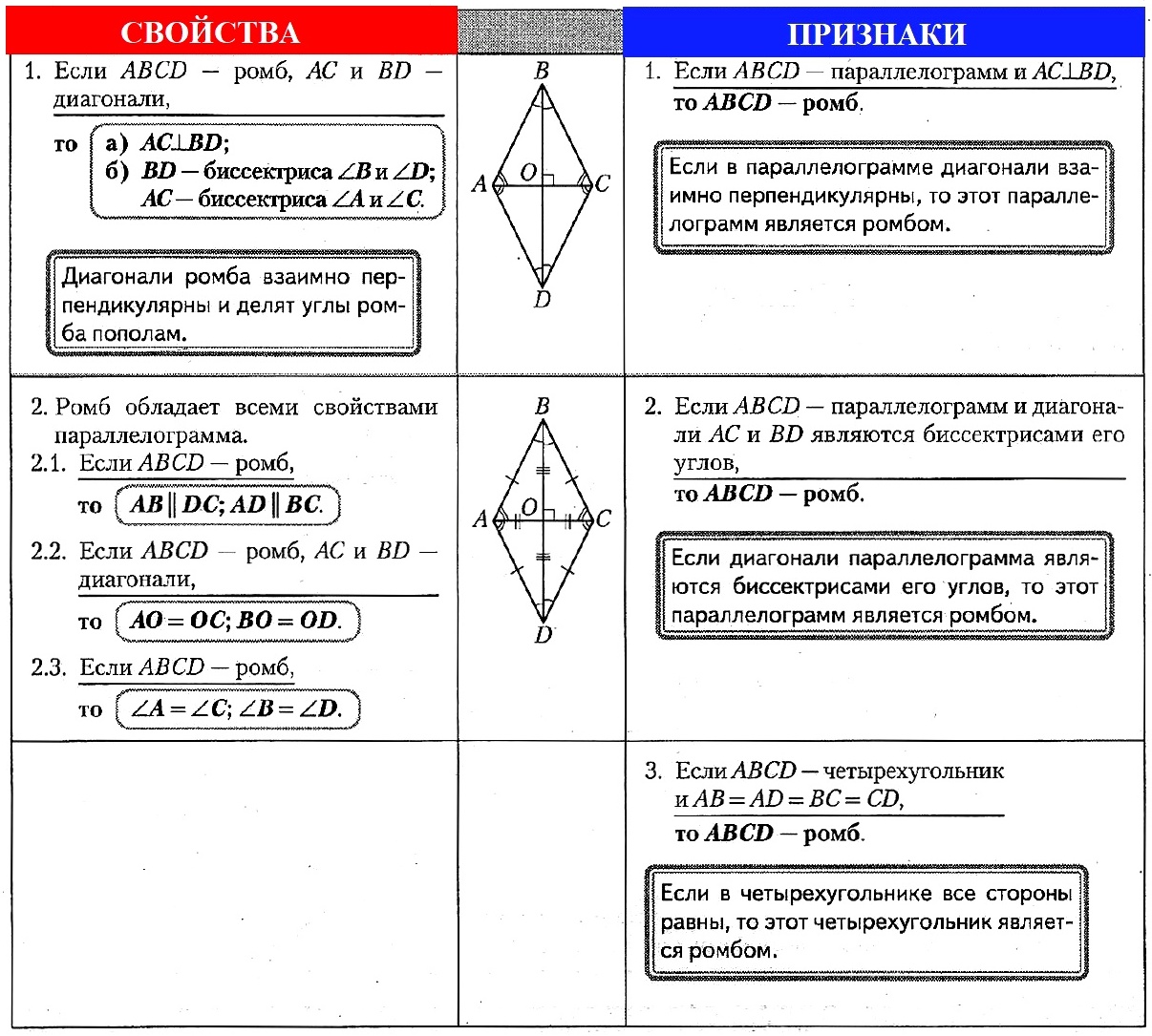
Параллелограмм, у которого все стороны равны, называется ромбом.

ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ

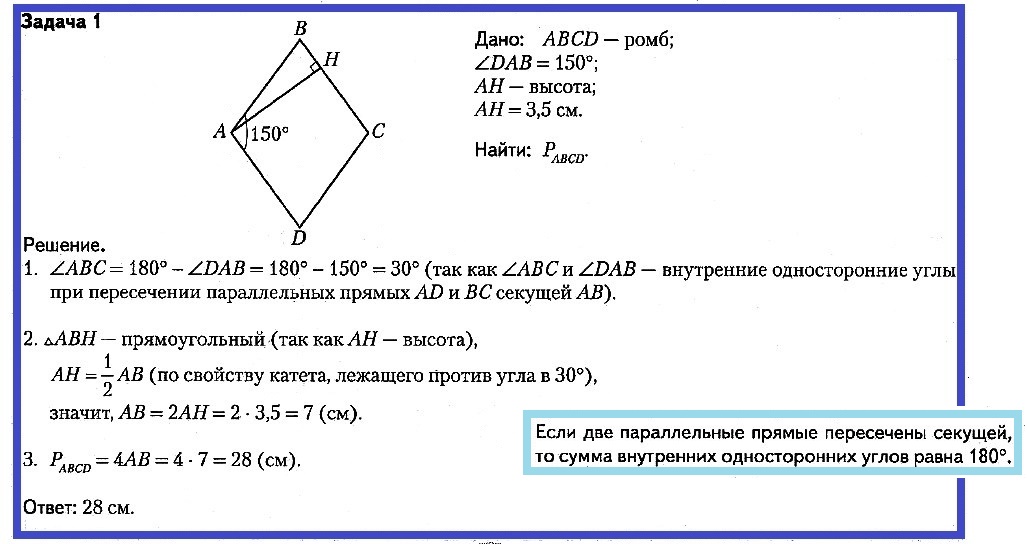
Задача № 1. Дано: ABCD — ромб; ∠DAB = 150°; AH — высота; AH = 3,5 см. Найти: P_ABCD

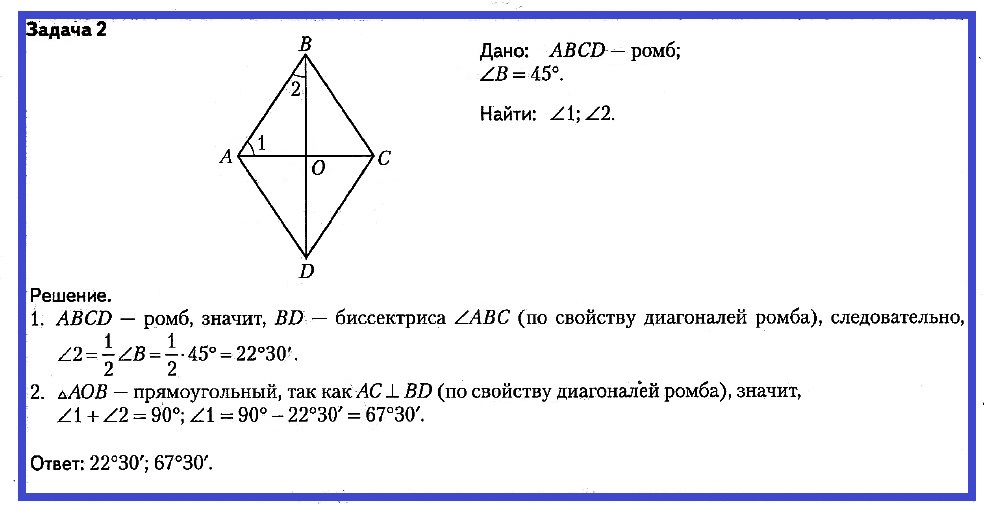
Задача № 2. Дано: ABCD — ромб; ∠B = 45°. Найти: ∠1, ∠2.

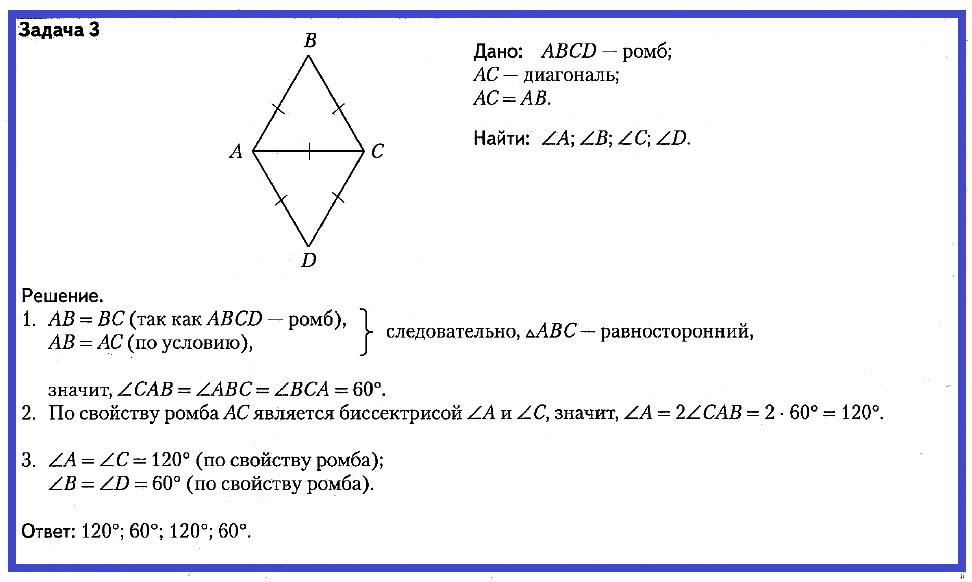
Задача № 3. Дано: ABCD — ромб; AC — диагональ; AC = AB. Найти: ∠A, ∠B, ∠C, ∠D.

Задача № 4. Дано: ABCD — ромб; AC, BD — диагонали; ∠ABD : ∠BAC = 4 : 5. Найти: ∠A, ∠B, ∠C, ∠D.

Это конспект по теме «ЗАДАЧИ по теме Ромб». Выберите дальнейшие действия:

Добавить комментарий Отменить ответ

Конспекты по геометрии:

7 класс

• Начальные геометрические понятия
• Аксиомы планиметрии
• Угол. Смежные и вертикальные углы
• Опорные задачи по теме УГЛЫ
• Параллельные прямые
• ЗАДАЧИ по теме Параллельные прямые
• Перпендикулярные прямые
• Треугольник. Равенство треугольников
• ЗАДАЧИ на Признаки равенства треугольников
• Равнобедренный треугольник + ЗАДАЧИ
• Свойства сторон и углов треугольника + ЗАДАЧИ
• Прямоугольный треугольник
• ЗАДАЧИ по теме Прямоугольные треугольники
• Расстояние от точки до прямой (ЗАДАЧИ)
• Геометрия 7 ЗАДАЧИ на построение
• Мерзляк Геометрия 7 Глава 1 Простейшие геометрические фигуры
• Мерзляк Геометрия 7 Глава 2 Треугольники
• Мерзляк Геометрия 7 Глава 3 Параллельные прямые. Сумма углов Δ
• Мерзляк Геометрия 7 Глава 4 Окружность и круг. Геометрические построения
• Краткий курс геометрии 7 класс
• Прямая. Окружность. Угол (опорный конспект)
• Задачи по теме «Прямая. Окружность. Угол»
• Треугольники (опорный конспект)
• Ключевые задачи по теме Треугольники
• Параллельные прямые (опорный конспект)
• Ключевые задачи про Параллельные прямые
• Сумма углов треугольника (опорный конспект)
• Ключевые задачи по теме: Сумма углов треугольника

8 класс

• Ломаная. Многоугольник + ЗАДАЧИ
• Четырехугольник и его свойства
• Параллелограмм: свойства и признаки
• ЗАДАЧИ по теме Параллелограмм
• Прямоугольник и его свойства
• ЗАДАЧИ по теме Прямоугольники
• Ромб и его свойства
• ЗАДАЧИ по теме Ромб
• Квадрат и его свойства
• ЗАДАЧИ по теме Квадрат
• Трапеция и её свойства
• Средняя линия треугольника
• Центральный угол. Вписанный угол
• Описанная и вписанная окружности четырехугольника
• Мерзляк Геометрия 8 Глава 1 Четырехугольники
• Краткий курс геометрии 8 класс
• Мерзляк Геометрия 8 Глава 2 Подобие треугольников
• Мерзляк Геометрия 8 Глава 3
• Мерзляк Геометрия 8 Глава 4 Многоугольники
• Площадь ромба. Формулы и Калькулятор
• Геометрия 8 Погорелов: все теоремы и определения

9 класс

• Опорный конспект 1. Окружности
• Опорный конспект 2. Описанные и вписанные окружности
• Опорный конспект 3. Теорема синусов. Теорема косинусов
• Опорный конспект 4. Правильные многоугольники

Найти конспект:

О проекте

Сайт «УчительPRO» — некоммерческий школьный проект учеников, их родителей и учителей. Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie и других пользовательских данных в целях функционирования сайта, проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.

Возрастная категория: 12+

(с) 2021 Учитель.PRO — Копирование информации с сайта только при указании активной ссылки на сайт!

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Нахождение радиуса вписанной в ромб окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в ромб. Также разберем примеры решения задач для закрепления изложенного материала.

Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

Формулы вычисления радиуса вписанной в ромб окружности

Через диагонали и сторону

Радиус r вписанной в ромб окружности равняется произведению его диагоналей, деленному на сторону, умноженную на 4.

• d₁ и d₂ – диагонали ромба;
• a – сторона ромба.

Через диагонали

Радиус r вписанной в ромб окружности можно найти, зная только длины его обеих диагоналей:

Эту формулу можно получить, если сторону a в формуле выше выразить через диагонали (согласно одному из свойств ромба):

Через сторону и угол

Радиус окружности r, вписанной в ромб, равняется половине произведения его стороны и синуса любого угла.

Через высоту

Радиус вписанного в ромб круга равняется половине его высоты.

Видео:Задача 6 №27914 ЕГЭ по математике. Урок 132Скачать

Примеры задач

Задание 1
Известно, что диагонали ромба равны 6 и 8 см. Найдите радиус окружности, вписанной в него.

Решение
Применим соответствующую формулу, подставив в нее известные значения:

Задание 2
Вычислите радиус вписанного в ромб круга, если его сторона равна 11 см, а один из углов – 30°.

Решение
В данном случае мы можем воспользоваться последней из рассмотренных выше формул:

Видео:Ромб. 8 класс.Скачать

Ромб: задачи на свойства

Летняя математическая онлайн-школа, задание 6 июля для 8 класса. Повторяем определение, свойства и признаки ромба. Разбираем как решать ключевые задачи на ромб.

Ромб — это параллелограмм, у которого все стороны равны.

Ромб обладает всеми свойствами параллелограмма и имеет свои.

Свойства ромба

1.В ромбе противоположные стороны и углы равны.

2. Противоположные стороны параллельны.

3. Сумма углов, прилежащих к одной стороне, составляет 180°.

4. Диагонали ромба пресекаются и точкой пресечения делятся пополам.

5. Диагонали ромба взаимно перпендикулярны.

6. Диагонали ромба являются биссектрисами углов.

Признаки ромба

1. Если в четырехугольнике все стороны равны, то этот четырехугольник является ромбом.

2. Если в четырехугольнике диагонали перпендикулярны и точкой пересечения делятся пополам, то этот четырехугольник является ромбом.

3. Если в параллелограмме диагонали взаимно перпендикулярны, то этот параллелограмм является ромбом.

4. Если в параллелограмме диагональ лежит на биссектрисе его угла, то эта фигура ромб.

5. Если в параллелограмме высоты равны, то этот параллелограмм является ромбом.

Реши задачи на ромб и отправь на проверку.

Ключевые задачи на ромб из ОГЭ

Задача 1

Один из углов ромба равен 43°. Найдите больший угол ромба.

Так как в ромбе противолежащие углы равны, то получаются две пары равных углов по 43°.

Чтобы найти вторую пару углов, нужно воспользоваться свойством углов при одной стороне ромба. Сумма таких углов равна 180°.

Один из суммы углов равен 43°. Найдем второй угол. 180° — 43° = 137°. Это и есть больший угол ромба.

Задача 2

В ромбе ABCD угол ABC равен 72°. Найдите угол ACD.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Нахождение радиуса вписанной в ромб окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в ромб. Также разберем примеры решения задач для закрепления изложенного материала.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Формулы вычисления радиуса вписанной в ромб окружности

Через диагонали и сторону

Радиус r вписанной в ромб окружности равняется произведению его диагоналей, деленному на сторону, умноженную на 4.

• d₁ и d₂ – диагонали ромба;
• a – сторона ромба.

Через диагонали

Радиус r вписанной в ромб окружности можно найти, зная только длины его обеих диагоналей:

Эту формулу можно получить, если сторону a в формуле выше выразить через диагонали (согласно одному из свойств ромба):

Через сторону и угол

Радиус окружности r, вписанной в ромб, равняется половине произведения его стороны и синуса любого угла.

Через высоту

Радиус вписанного в ромб круга равняется половине его высоты.

Видео:Геометрия 8. Урок 5 -Прямоугольник, ромб, квадрат - решение задач.Скачать

Примеры задач

Задание 1
Известно, что диагонали ромба равны 6 и 8 см. Найдите радиус окружности, вписанной в него.

Решение
Применим соответствующую формулу, подставив в нее известные значения:

Задание 2
Вычислите радиус вписанного в ромб круга, если его сторона равна 11 см, а один из углов – 30°.

Решение
В данном случае мы можем воспользоваться последней из рассмотренных выше формул:

Видео:Радиус вписанной в ромб окружности (6701)Скачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Геометрия В ромб, который делится своей диагональю на два равносторонних треугольника, вписанаСкачать

В ромб вписана окружность

Когда в условии задачи сказано, что в ромб вписана окружность, в ходе ее решения может быть использовано одно из следующих рассуждений.

Точка касания вписанной в ромб окружности делит его сторону на отрезки

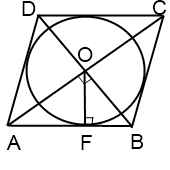
В этом случае радиус ромба и его диагонали можно найти, используя соотношения в прямоугольном треугольнике.

Например, F — точка касания вписанной в ромб окружности — делит сторону AB на отрезки AF=m, FB=n. О — центр вписанной в ромб окружности — является точкой пересечения его диагоналей. Треугольник AOB — прямоугольный (так как диагонали ромба взаимно перпендикулярны).

— как радиус, проведенный в точку касания. Значит, OF — высота, проведенная к гипотенузе. Отсюда

Высота ромба через радиус вписанной окружности

Радиус вписанной в ромб окружности

Радиус вписанной окружности можно найти по формуле

S — площадь ромба, p — его полупериметр (p=2a, где a — сторона ромба).

Соответственно, площадь ромба через радиус вписанной в него окружности

Поскольку площадь ромба также равна

Площадь ромба через отрезки, на которые делит сторону ромба точка касания вписанной в него окружности, может быть найдена как

Видео:ГЕОМЕТРИЯ 8 класс: Задача на ромбСкачать

Нахождение радиуса вписанной в ромб окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в ромб. Также разберем примеры решения задач для закрепления изложенного материала.

Видео:8 класс, 8 урок, Ромб и квадратСкачать

Формулы вычисления радиуса вписанной в ромб окружности

Через диагонали и сторону

Радиус r вписанной в ромб окружности равняется произведению его диагоналей, деленному на сторону, умноженную на 4.

• d₁ и d₂ – диагонали ромба;
• a – сторона ромба.

Через диагонали

Радиус r вписанной в ромб окружности можно найти, зная только длины его обеих диагоналей:

Эту формулу можно получить, если сторону a в формуле выше выразить через диагонали (согласно одному из свойств ромба):

Через сторону и угол

Радиус окружности r, вписанной в ромб, равняется половине произведения его стороны и синуса любого угла.

Через высоту

Радиус вписанного в ромб круга равняется половине его высоты.

Видео:№700. Докажите, что в любой ромб можно вписать окружность.Скачать

Примеры задач

Задание 1
Известно, что диагонали ромба равны 6 и 8 см. Найдите радиус окружности, вписанной в него.

Решение
Применим соответствующую формулу, подставив в нее известные значения:

Задание 2
Вычислите радиус вписанного в ромб круга, если его сторона равна 11 см, а один из углов – 30°.

Решение
В данном случае мы можем воспользоваться последней из рассмотренных выше формул:

Видео:Площадь ромба. Легче понять...Скачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

В ромб вписана окружность

Когда в условии задачи сказано, что в ромб вписана окружность, в ходе ее решения может быть использовано одно из следующих рассуждений.

Точка касания вписанной в ромб окружности делит его сторону на отрезки

В этом случае радиус ромба и его диагонали можно найти, используя соотношения в прямоугольном треугольнике.

Например, F — точка касания вписанной в ромб окружности — делит сторону AB на отрезки AF=m, FB=n. О — центр вписанной в ромб окружности — является точкой пересечения его диагоналей. Треугольник AOB — прямоугольный (так как диагонали ромба взаимно перпендикулярны).

— как радиус, проведенный в точку касания. Значит, OF — высота, проведенная к гипотенузе. Отсюда

Высота ромба через радиус вписанной окружности

Радиус вписанной в ромб окружности

Радиус вписанной окружности можно найти по формуле

S — площадь ромба, p — его полупериметр (p=2a, где a — сторона ромба).

Соответственно, площадь ромба через радиус вписанной в него окружности

Поскольку площадь ромба также равна

Площадь ромба через отрезки, на которые делит сторону ромба точка касания вписанной в него окружности, может быть найдена как

🎦 Видео

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Задача про ромб по геометрииСкачать

Окружность вписана в треугольник так,что образует у вершины ромбСкачать

Задача.Окружность и прямоугольник вписаны в квадрат.Скачать