Задачи на равновеликие треугольники

Разделы: Математика

Одними из самых древних являются задачи на равенство площадей (равновеликость), поскольку как раз при измерении площадей в Египте и зарождалась геометрия

Историк Геродот (V век до н. э) писал: “Если Нил заливал чей-нибудь участок, то пострадавший обращался к царю и докладывал ему о случившемся. Тогда царь посылал землемеров (геометров); они измеряли, на сколько уменьшился участок и сообразно этому уменьшали налог. Вот откуда возникла геометрия (землемерие)”

В книгах “Начала” Евклида равновеликость фигур означает, что они могут быть составлены из частей. Именно этими средствами, не прибегая даже к пропорциям, Евклид доказывает, что каждый многоугольник может быть преобразован в равновеликий (равносоставленный) треугольник, а треугольник — в квадрат.

Рассмотрим простейшие случаи равенства площадей

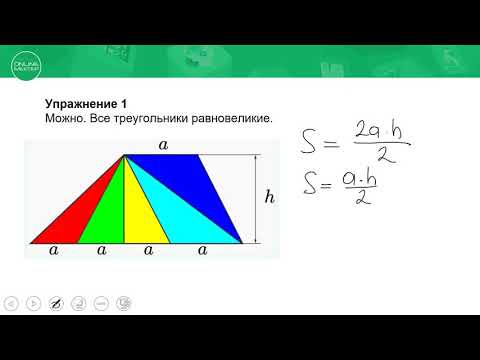
1. а || СВ. Все треугольники СВ равновелики (рис1)т.к. имеют общее основание и высоту.

2. Медиана треугольника делит его на два равновеликих треугольника (докажите)

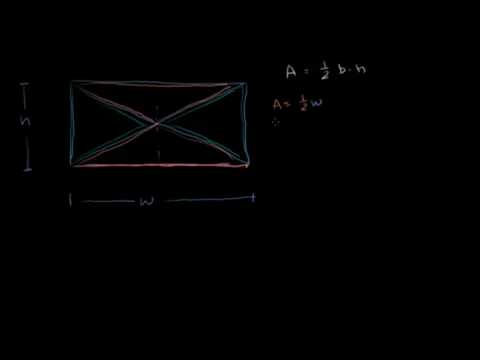
3. Диагонали параллелограмма делят его на 4 равновеликих треугольника

Доказательство: = и = (имеют равные основания и общую высоту), аналогично

+= +, следовательно: = = =

Решим задачи, используются свойства равновеликости фигур

Задача 1 Дан параллелограмм АВСD и точка М вне плоскости параллелограмма (рис 4) Проведите через точку М прямую, делящую его на две равновеликие фигуры

Решение: Проведем диагонали АС и ВD, которые пересекутся в точке О.Прямая МО будет искомой. Она разбивает параллелограмм на две трапеции, у которых равные высоты и равные средние линии РО = КО.

Задача 2. В параллелограмме АВСD вырезали отверстие в виде прямоугольника. Провести прямую так, чтобы разделить оставшуюся часть на две равновеликие фигуры

Решение: Проведем диагонали параллелограмма и прямоугольника. Через точки пересечения диагоналей О и М проведем прямую ОМ. Данная прямая будет искомой (см. предыдущую задачу) (еще один образец решения задачи)

Задача 3 Диагонали трапеции делят ее на 4 треугольника. Докажите, что треугольники, прилегающие к боковым сторонам трапеции, равновелики.

Решение = Если из равных площадей отнять одну и туже площадь, то оставшиеся площади будут равны.

Задача 4 На основаниях ВС и АD трапеции АВСD произвольно взяты точки М и К(рис 7) МА и МD пересекаются с КВ и КС в точках Е и N соответственно. Докажите, что площадь четырехугольника ЕМNК равна сумме площадей треугольников АВЕ и DNC

Решение. Обозначим площади треугольников через и , четырехугольника — Соединим точки М и К получим две трапеции АВМК и КМСD. Площади треугольников, прилежащих к боковым сторонам равны (доказано в задаче 3).Следовательно, + ,=

Задача 5 В трапеции СD (рис9) ВК || СD, где К АС. Докажите, что треугольники АВС и КСD равновелики

Решение В трапеции АВСD = (задача 3), в трапеции KBCD = Сложим равные площади, получим =.

Для нахождения площади произвольного многоугольника его обычно разбивают на треугольники и находят площадь каждого из них. Сумма площадей этих треугольников равна площади данного многоугольника. Площадь многоугольника можно найти другими способами. Один из таких способов был указан Евклидом. Он состоит в построении треугольника равновеликого данному.

Дан выпуклый пятиугольник АВСDЕ построим равновеликий ему треугольник. Для этого через вершину В проведем прямую, параллельную диагонали АС и через точку D прямую параллельную диагонали СЕ (рис 10).

AFBC трапеция по построению следовательно = (общее основание АС и высота)

Аналогично EKDC трапеция и = Таким образом =

Применяя способ Евклида к трапеции, получаем другой способ вывода площади трапеции.

Рассмотрим трапецию АВСD с основаниями АD = а и ВС = в и высотой h Проведем через вершину В прямую СЕ || ВD , тогда = Четырехугольник ВСЕD параллелограмм, поэтому ЕD = ВС = в. Итак, = (a +b)h

Докажем еще одну формулу для площади трапеции

Доказать, что площадь трапеции равна произведению боковой стороны и перпендикуляра, проведенного из середины другой боковой стороны к прямой содержащей первую сторону

Пусть в трапеции АВСD точка Е –середина СD, а EF –перпендикуляр к АВ через точку Е(рис 12) Проведем прямую, параллельную АВ и пересекающую прямые АD и ВС в точках К и М соответственно. АМВК – параллелограмм и = FD · EF. Этот параллелограмм и трапеция АВСD равносоставлены, следовательно, равновелики, значит = AB · EF

Литература:

1. Атанасян Л С Геометрия Дополнительные главы к учебнику Москва 2006.
2. Шарыгин. И Ф Геометрия Задачи М.Дрофа 1997.

Видео:Равновеликие треугольники. Треугольники с одинаковыми площадямиСкачать

Равновеликие фигуры — свойства, формулы и примеры

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Равные многоугольники

По определению равные фигуры должны быть во всём одинаковыми, включая площадь, длину сторон, размер углов и другие параметры. Чтобы рассмотреть всё из них, уйдёт много времени, да это и не нужно, ведь они взаимозависимы. Хорошим примером будет самый простой многоугольник — треугольник. Существует несколько правил, по которым можно определить, равны ли 2 треугольника между собой или нет:

1. По трём сторонам.
2. По стороне и двум прилегающим к ней углам.
3. По двум сторонам и углу между ними.

Нельзя путать первое условие с тремя углами. Ведь если в треугольнике равны 3 угла, они необязательно будут равными, но будут подобными.

Названия условий достаточно точно описывают критерии, по которым можно определить одинаковые 2 треугольника или нет. Из них следует, что необязательно знать все параметры: часто хватает только нескольких из них для определения «равности».

В большинстве случаев определить одинаковость других фигур гораздо сложнее, нежели треугольников. К счастью, чаще всего в школьной геометрии такой класс задач не рассматривают или даются дополнительные данные, помогающие с решением.

Например, доказательство «равности» для четырёхугольника сложнее, да и почти не встречается. Но если по условию сказано, что четырёхугольник не произвольный, а имеет прямые углы, задача становится проще. В таком случае рассматривается прямоугольник. А для него достаточно, чтобы 2 не противолежащие стороны были равны.

Если указано ещё и условие, что прямоугольник является квадратом, достаточно указать, что у двух таких фигур совпадает по длине одна сторона и уже этого будет достаточно.

Видео:Равновеликие треугольникиСкачать

Равность правильных фигур

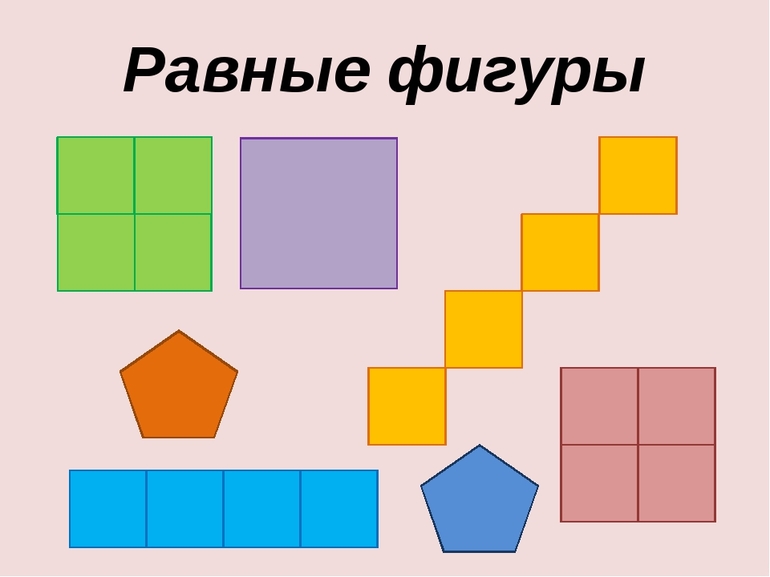
Частным и самым простым для сравнения является случай, когда многоугольник по условию правильный. Так называется фигура с одинаковыми сторонами и углами. Например, равносторонний треугольник и квадрат. Важно не забывать проверить равны ли углы, так как не каждая фигура правильная. Тот же ромб по определению имеет 4 совпадающие по длине стороны, но разные углы. При сравнении правильных многоугольников достаточно указать, что, хотя бы одна сторона фигуры равна стороне у другой. Это будет достаточное условие для доказательства «равности».

Самым простым и наглядным способом сверки двух фигур будет не геометрический с помощью правил, а путём наложения рисунков друг на друга. Разумеется, что он не претендует на точность, но изобразить параллелограмм и наложить его на другой нагляднее, чем сравнивать, например, углы. Понятно, что так можно только ознакомиться с концепцией «равности» и показать, какие фигуры называются равными, для упрощения в дальнейшем решения задач, но доказывать что-либо нельзя, ввиду неточности метода.

Если при сравнении двух тел оказывается, что их площади равны, такие тела (многоугольники) являются равновеликими. Как и в случае с прошлым, это определение звучит несложно. Проблемы могут начаться непосредственно при вычислении площадей. Самый простой многоугольник — треугольник. Для вычисления его площади существует множество способов.

Видео:Треугольники. Практическая часть - решение задачи. 7 класс.Скачать

Вычисление площади треугольника

Чаще всего приходится работать с прямоугольными треугольниками. Их площадь вычислить несложно — это полупроизведение катетов (сторон, между которыми лежит прямой угол). Таким образом, даже если стороны двух фигур по длине разные, но их произведение равно, они равновеликие. Например, треугольник с катетами 4 и 4 равен по площади многоугольнику с катетами 16 и 1. Так как их полупроизведение, а значит и площадь равна 8.

Если же треугольник произвольный (то есть не является частным случаем — прямоугольным, равнобедренным или равносторонним), можно воспользоваться одной из 5 формул, позволяющих вычислить его площадь.

1. По двум сторонам и углу между ними.
2. По стороне и высоте, проведённой к ней.
3. По трём сторонам и полупериметру.
4. По полупериметру и радиусу вписанной окружности.
5. По трём сторонам и радиусу описанной окружности.

То, какую формулу использовать, будет зависеть от данных, предоставленных в задаче. Иногда придётся проводить дополнительное построение, например, провести высоту или использовать свойства, что биссектрисы пересекаются в центре вписанной окружности. Если не даны все 3 стороны, использовать третью формулу не получится.

Важно понять, что фигуры могут быть разными по количеству углов, но всё равно считаться равновеликими — в учёт идёт только площадь, остальные параметры не важны. Например, прямоугольный треугольник с катетами 2 и 4 будет визуально казаться больше, чем квадрат со стороной 2, но их площади совпадают и равны 4 (площадь прямоугольника считается как произведение прилежащих сторон друг на друга). По определению это делает их равновеликими.

Видео:Задача 47. Оценка + пример. Найти наименьшее количество равновеликих треугольниковСкачать

Визуальный способ

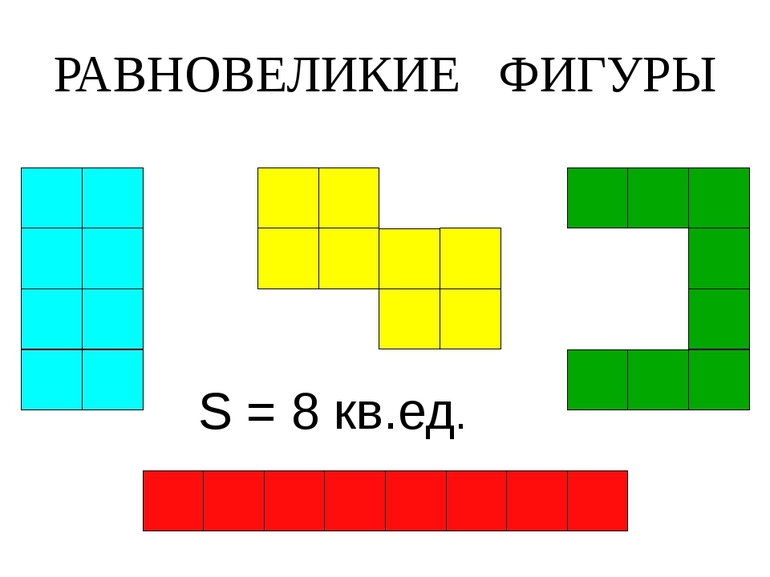
Существует также наглядный, но неточный способ. Нужно взять листок в клеточку и нарисовать на нём многоугольники. Если рисунок получился большой — не страшно, так будет только проще в дальнейшем. Следующий шаг — посчитать количество клеток, которое заняла каждая фигура и сравнить. Если оно равно, равновеликость доказана. Опять же метод не точный, но для введения в концепцию площадей и их «равности» подойдёт.

Иногда встречается словосочетание «равносоставленная фигура». Такими называют произвольные многоугольники, которые можно составить друг из друга путём разрезания одного из них на одинаковые объекты и перекладывания. Например, если прямоугольник 4 на 1 нарезать на одинаковые части — квадраты 1 на 1, то из полученных маленьких квадратов можно составить один большой со стороной 2. Но это не более чем забавное свойство некоторых фигур и в геометрии фактически почти не используется.

Видео:Запомни: все формулы для площади треугольникаСкачать

Медиана делит площадь треугольника пополам

Медиана делит площадь треугольника пополам

Два треугольника называются равновеликими. Если они имеют одинаковую площадь.

Теорема 1. Медиана делит треугольник на два равновеликих треугольника.

Пусть ВМ – медиана треугольника АВС. Докажем, что

.

Проведем высоту BH треугольника АВС. Тогда

,

.

Так как ВМ – медиана треугольника АВС, то АМ=МС, поэтому

.

,

.

Что и требовалось доказать.

Теорема 2. Медианы треугольника разбивают его на шесть равновеликих треугольников.

Доказательство можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».

Из теоремы, в частности следует, что если точку пересечения медиан треугольника соединить со всеми его вершинами, то треугольник разобьется на три равновеликие части.

Задача 1 Две медианы треугольника взаимно перпендикулярны и равны соответственно 3 и 4. Найти площадь треугольника.

Пусть в треугольнике АВС медианы АМ и ВЕ равны 3 и 4 соответственно, , К – точка пересечения медиан.

,

.

Так как треугольник АВК прямоугольный с прямым углом ВКА, то .

Так как медиан делят треугольник на 6 равновеликих частей, то .

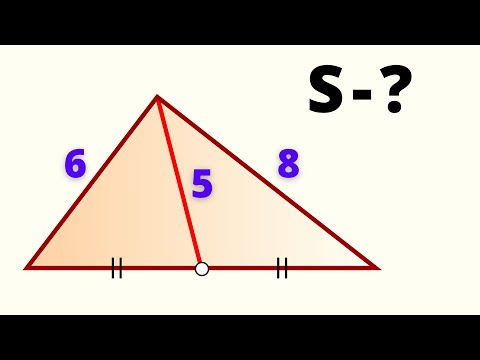
Задача 2 Медианы треугольника равны 6, 8 и 10, найти площадь треугольника.

Пусть медианы АM, BE и CD данного треугольника соответственно равны 6, 8 и 10, К – точка их пересечения. Отложим на продолжении луча ВЕ за точку Е отрезок EF=KE. Соединим точки С, F и A.

Рассмотрим треугольник KAF.

,

то

.

Далее, , так как CKAE – параллелограмм (по признаку параллелограмма: ели диагонали четырехугольника делятся точкой пересечения пополам, до данный четырехугольник параллелограмм), получаем .

Так как , то есть , то по обратной теореме Пифагора (если квадрат одной стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный) треугольник KAF – прямоугольный и .

Вычислим площадь треугольника AKF:

.

Теперь сравним площади треугольников AKF и АВС: так как AE – медиана треугольника AKF, то

, ,

.

.

Отметим, что задачу можно решить по-другому, если воспользоваться тем фактом, что:

площадь треугольника, образованного медианами данного треугольника составляет от площади самого треугольника.

Доказательство можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».

Вопросы для самопроверки:

1. Какие треугольники называются равновеликими?

2. Площадь треугольника равна S. Чему равна площадь каждого из треугольников, на которые его разбивает медиана, проведенная к какой-либо стороне этого треугольника?

3. На сколько равновеликих частей разбивают треугольник проведенные в нем три медианы?

4. Площадь треугольника равна S. Цент тяжести этого треугольника соединили с его вершинами. Чему равна площадь каждого из получившихся треугольников?

5. Площадь треугольника равна 48, чему равна площадь треугольника, составленного из медиан этого треугольника?

6. Площадь треугольника, составленного из медиан некоторого треугольника равна 24, чему равна площадь треугольника?

Задачи для самостоятельного решения:

1. Две медианы треугольника взаимно перпендикулярны и равны соответственно 6 и 8. Найти площадь треугольника.

2. Медианы треугольника равны 3, 4 и 5 найти площадь треугольника.

3. Треугольник АВС, стороны которого 13 см, 14 см и 15 см, разбит на три треугольника отрезками, соединяющими точку М пересечения медиан треугольника с вершинами треугольника. Найти площадь треугольника ВМС.

4. Две стороны треугольника равны 10 и 12, а медиана, проведённая к третьей, равна 5. Найдите площадь треугольника.

💥 Видео

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Площадь треугольника, медиана и равновеликие треугольники. ЗадачаСкачать

Задача, которую исключили из экзамена в АмерикеСкачать

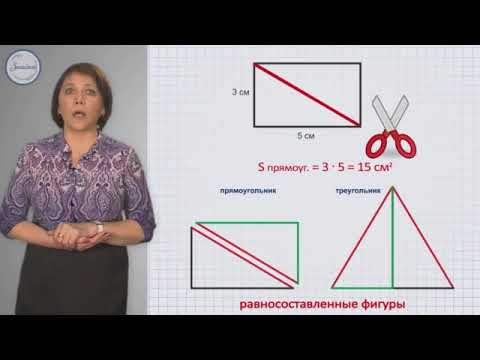
Равносоставленные и равновеликие фигуры 360pСкачать

90 задач по геометрии решается этим способом!Скачать

Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

8 класс. Геометрия. Равновеликость и равносоставленность фигур. 15.05.2020.Скачать

Многоугольники. Математика 8 класс | TutorOnlineСкачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Решали пол-урока, а оказалось очень простоСкачать

Медиана и равновеликие треугольники. Отношение синусов. Площадь треугольника. ЕГЭ. Геометрия.Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Задача, которую боятсяСкачать

Математика 3 класс. Равносоставленные и равновеликие фигурыСкачать