Задачи на окружности касающиеся внутренним образом (8 видео)

Касание окружностей

Говорят, что две окружности касаются, если они имеют единственную общую точку. Эта точка называется точкой касания окружностей. Касание окружностей бывает внутренним и внешним.

Содержание

Внутреннее касание
Внешнее касание
Подборка задач для работы на уроке по теме «Касание окружностей»
«Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
Решение
Решение
Решение
Решение
Задачи на окружности касающиеся внутренним образом
💥 Видео

Видео:ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать

Внутреннее касание

Касание называется внутренним, если центры окружностей лежат по одну сторону от точки касания окружностей. Построим две окружности, первая с центром A и радиусом AC, отметим на радиусе AC точку B, это будет центр второй окружности с радиусом BC:

Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внутренним образом.

При внутреннем касании двух окружностей, расстояние между их центрами равно разности их радиусов.

Видео:Задача. Две окружности касаются внутренним образом.Скачать

Внешнее касание

Касание называется внешним, если центры окружностей лежат по разные стороны от точки касания. Построим две окружности, первая с центром A и радиусом AC, вторая с центром B и радиусом BC:

Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внешним образом.

При внешнем касании двух окружностей, расстояние между их центрами равно сумме их радиусов.

Видео:Окружности касаются внутренним образом.мой вариант решения задачи.#hard.Скачать

Подборка задач для работы на уроке по теме «Касание окружностей»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Геометрия Две окружности касаются внутренним образом в точке A, причем меньшая окружность проходитСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Материал по теме «Касание окружностей»

Подборка задач для работы на уроке и самоподготовке по теме

Касание окружностей бывает внешним и внутренним.

«окружности касаются внешним образом ».

«окружности касаются внутренним образом».

Если две окружности касаются, то точка касания лежит на прямой, соединяющей центры . Кроме того, эта п рямая перпендикулярна касательной , проведённой в точку касания окружностей.

Углом между двумя окружностями в точке их пересечения называется угол, образованный их касательными в этой точке.

Линия центров двух касающихся окружностей проходит через точку касания.

Концентрическими окружностями называются окружности с общим центром.

Если — расстояние между центрами окружностей радиусов и общая внешняя касательная касается окружностей в точках и общая внутренняя в точках и то

Если две окружности внешне касаются в точке С и их общая внутренняя касательная, проведённая через С, пересекается в точке D с другой общей внешней касательной АВ (А и В –точки касания), то АВ=2С D

Две окружности касаются в точке A . К ним проведена общая (внешняя) касательная, касающаяся окружностей в точках C и B . Докажите, что CAB = 90 o .

Пусть M — точка пересечения прямой CB и касательной к окружностям в точке A . Тогда MC = MA = MB (равенство отрезков касательных). Поэтому точка A лежит на окружности с диаметром CB .

Равенство отрезков касательных,

Вписанный прямоугольный треугольник.

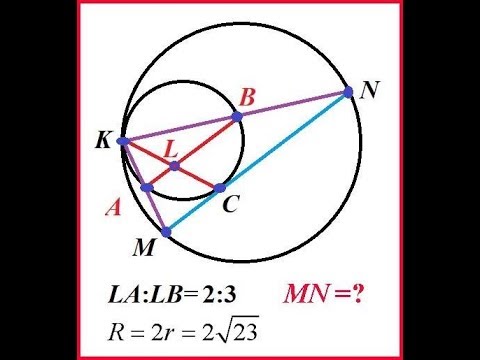
Окружности радиусов r и R ( R > r ) касаются внешним образом в точке K . К ним проведены две общие внешние касательные. Их точки касания с меньшей окружностью — A и D , с большей — B и C соответственно.

а) Найдите AB и отрезок MN общей внутренней касательной, заключённый между внешними касательными.

б) Докажите, что углы AKB и O ₁ MO ₂ — прямые ( O ₁ и O ₂ — центры окружностей).

Решение

а) Опустим перпендикуляр O ₁ P из центра O ₁ на O ₂ B . Из прямоугольного треугольника O ₁ PO ₂ находим, что

O₁O₂ = r + R, O₂P = R — r, O₁P = = 2.

Поэтому AB = O ₁ P = 2 .

Поскольку MK = MB и MK = MA , то

NM = 2 MK = AB = 2 .

б) Поскольку MO ₁ и MO ₂ — биссектрисы смежных углов AMK и BMK , то угол O ₁ MO ₂ — прямой.

Поскольку MA = MK = MB , то точка K лежит на окружности с диаметром AB . Поэтому AKB = 90 o .

а) Опустим перпендикуляр O ₁ P из центра O ₁ на O ₂ B . Из прямоугольного треугольника O ₁ PO ₂ находим, что

O₁O₂ = r + R, O₂P = R — r, O₁P = = 2.

Поэтому AB = O ₁ P = 2 .

Поскольку MK = MB и MK = MA , то

NM = 2 MK = AB = 2 .

б) Поскольку MO ₁ и MO ₂ — биссектрисы смежных углов AMK и BMK , то угол O ₁ MO ₂ — прямой.

Поскольку MA = MK = MB , то точка K лежит на окружности с диаметром AB . Поэтому AKB = 90 o .

а) Опустим перпендикуляр O ₁ P из центра O ₁ на O ₂ B . Из прямоугольного треугольника O ₁ PO ₂ находим, что

O₁O₂ = r + R, O₂P = R — r, O₁P = = 2.

Поэтому AB = O ₁ P = 2 .

Поскольку MK = MB и MK = MA , то

NM = 2 MK = AB = 2 .

б) Поскольку MO ₁ и MO ₂ — биссектрисы смежных углов AMK и BMK , то угол O ₁ MO ₂ — прямой.

Поскольку MA = MK = MB , то точка K лежит на окружности с диаметром AB . Поэтому AKB = 90 o .

Теорема Пифагора (прямая и обратная)

Даны две концентрические окружности радиусов 1 и 3 с общим центром O . Третья окружность касается их обеих. Найдите угол между касательными к третьей окружности, проведёнными из точки O .

Решение

Пусть O ₁ — центр третьей окружности, OA и OB — касательные к ней ( A и B — точки касания). Тогда OO ₁ — биссектриса угла AOB ,

AO ₁ = 1, OO ₁ = 2, OAO ₁ = 90 o .

Поэтому AOO ₁ = 30 o , а AOB = 60 o .

В окружности радиуса R проведён диаметр и на нём взята точка A на расстоянии a от центра. Найдите радиус второй окружности, которая касается диаметра в точке A и изнутри касается данной окружности.

Решение

Пусть O и O ₁ — центры данных окружностей, x — искомый радиус. В треугольнике OO ₁ A известно, что

По теореме Пифагора

Отсюда находим, что x = .

Две окружности Ω ₁ и Ω ₂ с центрами O ₁ и O ₂ касаются внешним образом в точке O . Точки X и Y лежат на Ω ₁ и Ω ₂ соответственно так, что лучи O ₁X и O ₂Y одинаково направлены. Из точки X проведены касательные к Ω ₂ , а из точки Y – к Ω ₁ . Докажите, что эти четыре прямые касаются одной окружности, проходящей через точку O .

Решение

Обозначим через S точку пересечения XO ₁ и YO ₁ (см. рис.). Пусть r ₁ и r ₂ – радиусы соответствующих окружностей. Тогда . Значит, SO || O ₂ Y и .

Пусть XZ – одна из касательных проведённых из точки X ко второй окружности, а Z ‘ – проекция S на XZ . Тогда .
Аналогично доказывается, что расстояние от S до остальных касательных также равно SO , то есть S и есть центр требуемой окружности.

Вспомогательные подобные треугольники

Теорема Фалеса и теорема о пропорциональных отрезках

1. Две касающиеся окружности с центрами O 1 и O 2 касаются внутренним образом окружности радиуса R с центром O . Найдите периметр треугольника OO 1 O 2.

2. Окружности S 1 и S 2 касаются окружности S внутренним образом в точках A и B , причём одна из точек пересечения окружностей S 1 и S 2 лежит на отрезке AB . Докажите, что сумма радиусов окружностей S 1 и S 2 равна радиусу окружности S .

3 . На отрезке AB взята точка C . Прямая, проходящая через точку C , пересекает окружности с диаметрами AC и BC в точках K и L , а окружность с диаметром AB —в точках M и N . Докажите, что KM = LN .

4. Даны четыре окружности S 1, S 2, S 3 и S 4, причём окружности Si и Si + 1 касаются внешним образом для i = 1, 2, 3, 4 ( S 5 = S 1). Докажите, что точки касания образуют вписанный четырёхугольник.

Видео:Поступайте правильно Математика ЕГЭСкачать

Задачи на окружности касающиеся внутренним образом

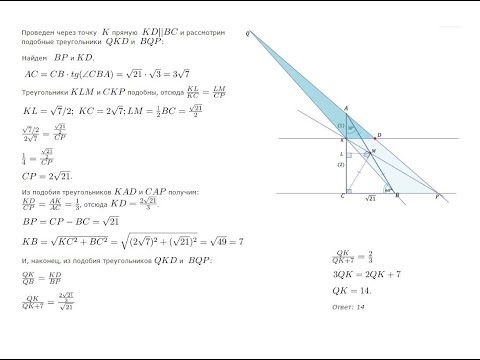
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.

а) Докажите, что прямые AD и BC параллельны.

б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

а) Обозначим центры окружностей O₁ и O₂ соответственно. Пусть общая касательная, проведённая к окружностям в точке K, пересекает AB в точке M. По свойству касательных, проведённых из одной точки, AM = KM и KM = BM. Треугольник AKB, у которого медиана равна половине стороны, к которой она проведена, — прямоугольный.

Вписанный угол AKD прямой, поэтому он опирается на диаметр AD. Значит, AD ⊥ AB. Аналогично получаем, что BC ⊥ AB. Следовательно, прямые AD и BC параллельны.

б) Пусть, для определенности, первая окружность имеет радиус 4, а радиус второй равен 1.

Треугольники BKC и AKD подобны, Пусть тогда

У треугольников AKD и AKB общая высота, следовательно, то есть S_AKB = 4S. Аналогично, S_CKD = 4S. Площадь трапеции ABCD равна 25S.

Вычислим площадь трапеции ABCD. Заметим, что Проведём к AD перпендикуляр O₂H, равный высоте трапеции, и найдём его из прямоугольного треугольника O₂HO₁:

Тогда

Следовательно, 25S = 20, откуда S = 0,8 и S_AKB = 4S = 3,2.

Приведем вариант решения п. б) предложенный Рамилем Багавиевым.

Из первого решения известно, что Из подобия треугольников AKD и AKB следует таким образом AK = 2BK. Напишем теорему Пифагора для треугольника AKB

Теперь несложно вычислить

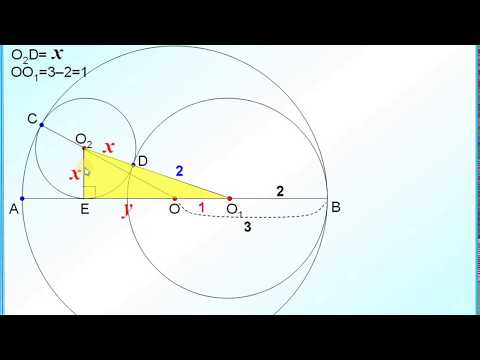
Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.

а) Докажите, что периметр треугольника с вершинами в центрах трёх окружностей равен диаметру наибольшей из этих окружностей.

б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 4 и 1.

а) Пусть АВ — диаметр большей из трёх окружностей, О — её центр, O₁ — центр окружности радиуса r у касающейся окружности с диаметром АВ в точке А, O₂ — центр окружности радиуса R, касающейся окружности с диаметром АВ в точке С, окружности с центром O₁ — в точке D, отрезка АВ — в точке Е. Точки О, O₂ и С лежат на одной прямой, поэтому OO₂ = ОС − O₂С = ОС − R. Аналогично ОО₁ = OA − О₁А = ОА − r и O₁O₂ = O₁D + O2D = r + R. Следовательно, периметр треугольника OO₁O₂ равен

а так как О₁E = OO₁ + ОЕ, то Полученное уравнение не имеет корней, что означает, что данная конфигурация невозможна.

Рассмотрим случай, когда точка Е лежит между точками О и А. В этом случае О₁E = OO₁ − ОЕ, то есть Из этого уравнения находим, что

Ответ:

Хорды AD, BE и CF окружности делят друг друга на три равные части.

а) Докажите, что эти хорды равны.

б) Найдите площадь шестиугольника ABCDEF, если точки A, B, C, D, E, F последовательно расположены на окружности, а радиус окружности равен

а) Пусть две хорды равны 3x и 3y. По теореме о произведении пересекающихся хорд 2x · x = 2y · y. Отсюда находим, что x = y, значит, эти хорды равны. Аналогично докажем, что третья хорда равна каждой из первых двух.

б) Равные хорды равноудалены от центра окружности, поэтому центр равностороннего треугольника с вершинами в точках попарного пересечения хорд совпадает с центром данной окружности. Пусть хорды BE и CF пересекают хорду AD в точках P и Q соответственно, хорды BE и FC пересекаются в точке T, а H — проекция центра O на хорду AD. Тогда H — общая середина отрезков AD и PQ, а OH — радиус вписанной окружности равностороннего треугольника PQT со стороной PQ.

Через точку T проведём прямую, параллельную AD, через точку P — прямую, параллельную CF, а через точку Q — прямую, параллельную BE. Эти прямые и хорды AD, BE и CF разбивают шестиугольник ABCDEF на 13 одинаковых равносторонних треугольников.

Обозначим PQ = 2a. Тогда

Отсюда находим, что a = 3, значит, PQ = 2a = 6,

Ответ:

Я решил другим, но верным способом через площади 6 равных треугольников, перепроверил с репититором, у нас выходит ответ 126 корней из 3. Кстати именно такого альтернативного способа не хватает в решении.

Наверное, в этот момент стоило бы сравнить ваше решение с нашим и попробовать найти ошибку. В математике все просто: или ошибка есть, или ее нет.

Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.

а) Докажите, что прямые KM и BC параллельны.

б) пусть L — точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.

а) Пусть O — центр большей окружности. Линия центров касающихся окружностей проходит через точку касания, поэтому OA — диаметр меньшей окружности.

Точка K лежит на окружности с диаметром OA, значит, ∠AKO = 90°. Отрезок OK — перпендикуляр, опущенный из центра большей окружности на хорду AB. Поэтому K — середина AB. Аналогично, M — середина AC, поэтому KM — средняя линия треугольника ABC. Следовательно, прямые MK и BC параллельны.

б) Опустим перпендикуляр OH на хорду BC. Тогда H — середина BC. Из прямоугольного треугольника OHB находим, что

Пусть Q — центр меньшей окружности. Тогда прямые QP и OH параллельны. Опустим перпендикуляр QF из центра меньшей окружности на OH. Тогда

PH 2 = QF 2 = QO 2 − OF 2 = 25 − 1 =24,

OP 2 = OH 2 + PH 2 = 36 + 24 = 60,

а из прямоугольного треугольника APO находим, что

Отрезок KM — средняя линия треугольника ABC, поэтому L средина AP. Следовательно,

Ответ: б)

Приведём решение Марии Ковалёвой (Москва).

а) Проведём общую касательную к окружностям AT, как показано на рисунке слева. Тогда и поскольку угол между касательной и хордой равен половине заключённой между ними дуги. Тогда равны Соответственные углы при пересечении прямых KM и BC равны, поэтому данные прямые параллельны.

б) По обобщенной теореме синусов, в треугольниках AKM и ABC стороны KM и BC относятся так же, как радиусы данных в условии окружностей, то есть как 1 : 2. Следовательно, KM — средняя линия треугольника ABC, и по теореме Фалеса. Осталось найти AР.

Опустим перпендикуляр OH на хорду BC (см. рисунок справа). Тогда H — середина BC. Из прямоугольного треугольника OHB находим, что

Треугольник OAP прямоугольный, так как угол OРA опирается на диаметр. Углы OAP и OPH равны по теореме об угле между касательной и хордой. Следовательно, прямоугольные треугольники OAP и OPH подобны по острому углу. Имеем: то есть Следовательно, По теореме Пифагора, Окончательно получаем:

Решение «сыпется», если концы хорды ВС расположить по разные стороны от диаметра (ОА). Тогда ОН, по-прежнему равный 6 из теоремы Пифагора, будет по чертежу меньше, чем параллельный ему радиус QP=5 меньшей окружности

Да, Ваше рассуждение доказывает, что этот случай невозможен.

Почему К середина АВ при условии,что ОК перпендикуляр? Что за свойство?

Свойство высоты равнобедренного треугольника. Треугольник ОАВ — равнобедренный, ОК — его высота, проведенная к основанию

Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй&nbsp— в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.

а) Докажите, что прямые AD и BC параллельны.

б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

Задание а). Обозначим центры окружностей и соответственно. Пусть общая касательная, проведённая к окружностям в точке K, пересекает AB в точке По свойству касательных, проведённых из одной точки, и. Треугольник AKB, у которого медиана равна половине стороны, к которой она проведена, — прямоугольный.