Задачи на доказательство равнобедренного треугольника

Равнобедренный треугольник — треугольнику которого две стороны равны.
Равные стороны называют боковыми сторонами, а третью сторону — основанием.

Свойства равнобедренного треугольника были известны с давних времен. Еще древние вавилоняне (II в. до н.э.) знали, что углы у основания равнобедренного треугольника равны. Любой треугольник можно разрезать на равнобедренные треугольники.

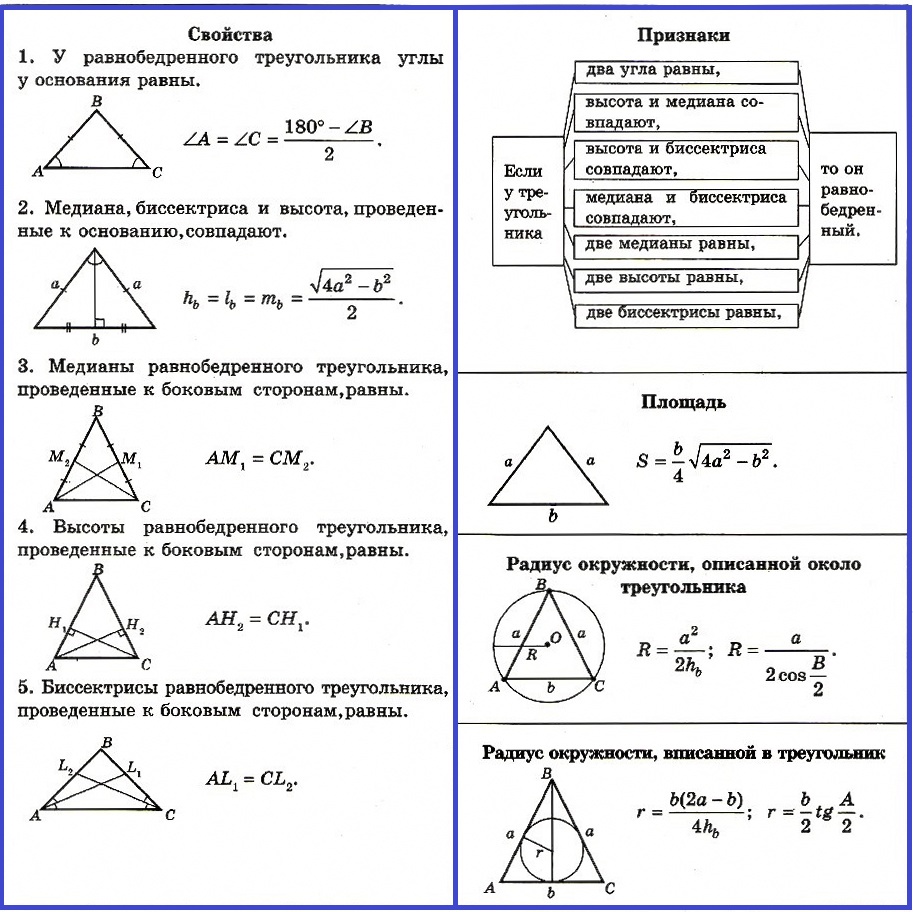
Свойства и признаки равнобедренного треугольника

Свойства равнобедренного треугольника:
1. У равнобедренного треугольника углы у основания равны (теорема).
2. Медиана, биссектриса и высота, проведенные к основанию, совпадают (теорема).
3. Медианы равнобедренного треугольника, проведенные к боковым сторонам, равны.
4. Высоты равнобедренного треугольника, проведенные к боковым сторонам, равны.
5. Биссектрисы равнобедренного треугольника, проведенные к боковым сторонам, равны.

Признаки равнобедренного треугольника:
Если у треугольника есть один из нижеуказанных признаков, то он равнобедренный:
— два угла равны,
— высота и медиана совпадают,
— высота и биссектриса совпадают,
— медиана и биссектриса совпадают,
— две медианы равны,
— две высоты равны,
— две биссектрисы равны.

ПРИМЕРЫ РЕШЕНИЯ
КЛЮЧЕВЫХ ЗАДАЧ:

Задача № 1. Дано: ΔABC — равносторонний, ΔADC — равнобедренный (AD=CD), AC — общая сторона, BC = 8 см, P_ADC > P_ABC в 1,5 раза. Найти: CD.

Задача № 2. Дано: ΔABC — равнобедренный, AB = BC, AD — медиана, AB + BD = 27 см, AC + CD = 21 см. Найти: AB, BC, AC.

Задача № 3. Дано: ΔABC — равнобедренный, AB = BC, ∠1 = 130°. Найти: ∠2.

Теоретический тест
с последующей самопроверкой

1. Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение:
   а) всегда верно;
   б) может быть верно;
   в) всегда неверно.
2. Если треугольник равносторонний, то:
   а) он равнобедренный;
   б) все его углы равны;
   в) любая его высота является биссектрисой и медианой.
3. В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
   а) в любом;
   б) в равнобедренном;
   в) в равностороннем.
4. Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
   а) всегда верно;
   б) может быть верно;
   в) всегда неверно.
5. Если треугольник равнобедренный, то:
   а) он равносторонний;
   б) любая его медиана является биссектрисой и высотой;
   в) два его угла равны.
6. В каком треугольнике любая его высота делит треугольник на два равных треугольника?
   а) в любом;
   б) в равнобедренном;
   в) в равностороннем.
7. Если в треугольнике два угла равны, то этот треугольник является:
   а) равносторонним;
   б) равнобедренным;
   в) прямоугольным.
8. Если в треугольнике две стороны равны, то:
   а) у него равны два угла;
   б) у него все углы равны;
   в) этот треугольник равносторонний.

1. Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение: б) может быть верно.
2. Если треугольник равносторонний, то: а) он равнобедренный; б) все его углы равны; в) любая его высота является биссектрисой и медианой.
3. В каком треугольнике только одна его высота делит треугольник на два равных треугольника? б) в равнобедренном.
4. Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение: а) всегда верно.
5. Если треугольник равнобедренный, то: в) два его угла равны.
6. В каком треугольнике любая его высота делит треугольник на два равных треугольника? в) в равностороннем.
7. Если в треугольнике два угла равны, то этот треугольник является: б) равнобедренным.
8. Если в треугольнике две стороны равны, то: а) у него равны два угла.

Вы смотрели конспект по теме «Равнобедренный треугольник + ЗАДАЧИ по теме». Выберите дальнейшие действия:

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Решение задач по теме РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

№ 107
Решение:
Р = 50 см;
х + 2х + 2х = 50 см;
х = 10 см;
АВ = ВС = 20 см,
АС= 10 см.

№ 111
Решение:
ACD = ABD по двум сторонам и углу между ними (CD = DB, AD — общая сторона,
2 = 1).
Тогда АС = АВ,
ABC – равнобедренный

Докажите, что медианы равнобедренного треугольника,
проведенные к равным боковым сторонам, равны
Решение :
 ADC =  СЕА по двум сторонам и углу между ними
(АС — общая сторона,
AD = СЕ = 1/2АВ = 1/2ВС
как половины равных боковых сторон,
DAC = ЕСА как углы при основании).
Тогда CD = АЕ.

Решение :
а) BDE = BDF по 1 признаку
(BD — общая сторона,
ВЕ = BF,
EBD = FBD, так как BD —
медиана и биссектриса).
№ 120
б) ADE = CDF по 1 признаку (AD = СD так как D середина АС, АЕ = CF по условию задачи, A = С как углы при основании равнобедренного треугольника).

№ 118
Дано: АВС — равнобедренный, ВС — основание; М, N  ВС; ВМ = CN.
Доказать:
а) ВАМ = CAN;
б)AMN— равнобедренный.
Доказательство: а) Рассмотрим
треугольники ВАМ и CAN. У них:
1) АВ = АС, так как по условию задачи ABC – равнобедренный с основанием ВС; 2) ВМ = CN no условию задачи; 3) АВМ = CAN как углы при основании равнобедренного треугольника.
Отсюда ВАМ = CAN по двум сторонам и углу между ними.

б) По доказанному в пункте а) ВАМ = CAN. В равных треугольниках соответственные стороны равны, то есть АМ = AN. Получили, что в AMN две стороны равны, т.е. AMN — равнобедренный.

№ 119
Решение: ЕЕ — биссектриса, проведенная из вершины равнобедренного треугольника к его основанию, и по свойству равнобедренного треугольника она является медианой и высотой. Если EF — медиана, то DF = FK, значит, KF = 1/2DK = 16/2 = 8 (см). Если ЕЕ— высота, то EF  DK, значит, EFD = 90°. Если EF— биссектриса, то DEK = 2 · DEF = 2 · 43° = 86°.
Ответ: KF = 8 см, DEK= 86°, EFD = 90°.
Дано: DEK— равнобедренный с основанием DK, DK= 16 см, EF— биссектриса, DEF = 43°.
Найти: KF, DEK, EFD.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 988 человек из 78 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 672 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 542 506 материалов в базе

Материал подходит для УМК

«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

18. Свойства равнобедренного треугольника

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 08.01.2022
• 15
• 0

• 08.01.2022
• 26
• 0

• 08.01.2022
• 50
• 0

• 07.01.2022
• 53
• 0

• 07.01.2022
• 68
• 0

• 07.01.2022
• 185
• 1

• 07.01.2022
• 52
• 0

• 07.01.2022
• 56
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 08.01.2022 78
• PPTX 3.8 мбайт
• 0 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Петрова Наталья Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 4 года и 9 месяцев
• Подписчики: 0
• Всего просмотров: 20788
• Всего материалов: 39

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Свойства равнобедренного треугольника. 7 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Рязанских школьников с 5 по 8 классы переведут на дистанционное обучение

Время чтения: 1 минута

В Омской области школы и колледжи перейдут на дистанционное обучение с 7 по 21 февраля

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Онлайн-семинар о развитии управляющих функций мозга ребенка

Время чтения: 1 минута

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

Петербургских школьников с 7 по 11 классы перевели на дистанционное обучение

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Равнобедренный треугольник. 7 класс.Скачать

Равнобедренный треугольник: свойства, признаки и формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Свойства равнобедренного треугольника. Практическая часть. 7 класс.Скачать

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Видео:ГЕОМЕТРИЯ 7 класс : Решение задач по теме "Равнобедренный треугольник"Скачать

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

1. Если у треугольника два угла равны, то этот треугольник — равнобедренный.
2. Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
3. Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
4. Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!

Видео:Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, AH = HC и BH — медиана.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, AH = HC и BH — медиана.

Видео:Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.

Значит, ∠A = ∠C = 80°.

Не должно вас удивить и то, что сумма углов треугольника равна 180°.

∠B = 180° − 80° − 80° = 20°.

Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.

Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.

А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.

Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.

Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.

📹 Видео

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Решение задач ( Равнобедренный треугольник) 7 классСкачать

Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Равнобедренный треугольник. Практическая часть. 7 класс.Скачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Признаки равнобедренного треугольника - геометрия 7 классСкачать

7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Задачи на доказательство по геометрии. Первый признак равенства треугольников.Скачать

Признаки равенства треугольников. 7 класс.Скачать

Первый признак равенства треугольников. 7 класс.Скачать

Задачи на доказательство равенства треугольников. Первый признак. Простые.Скачать