Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см.
Найдем отрезок DO: DO = OB − BD = 5 − 1 = 4. Так как OB перпендикулярен AC, треугольник AOD — прямоугольный. По теореме Пифагора имеем: 
. Треугольник AOC — равнобедренный так как AO = OC = r, тогда AD = DC. Таким образом, AC = AD·2 = 6.
Найдите величину (в градусах) вписанного угла α, опирающегося на хорду AB, равную радиусу окружности.
Проведем радиусы OA и OB. Так как по условию задачи хорда AB равна радиусу, то треугольник AOB — равносторонний, следовательно, все его углы равны 60°. Угол AOB — центральный и равен 60° Угол ACB — вписанный и опирается на ту же дугу, что и угол AOB. Таким образом, 
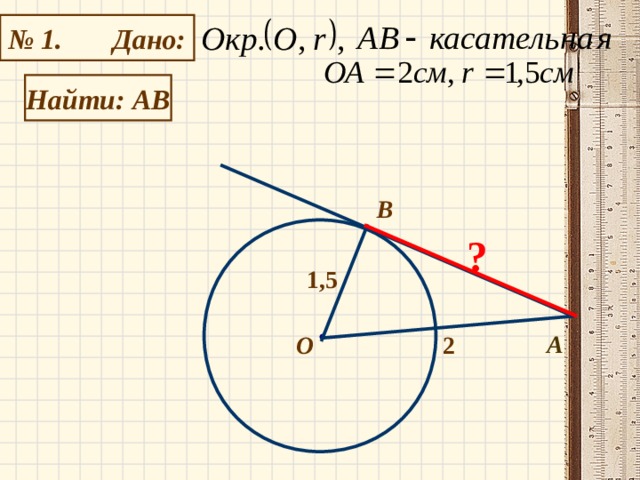
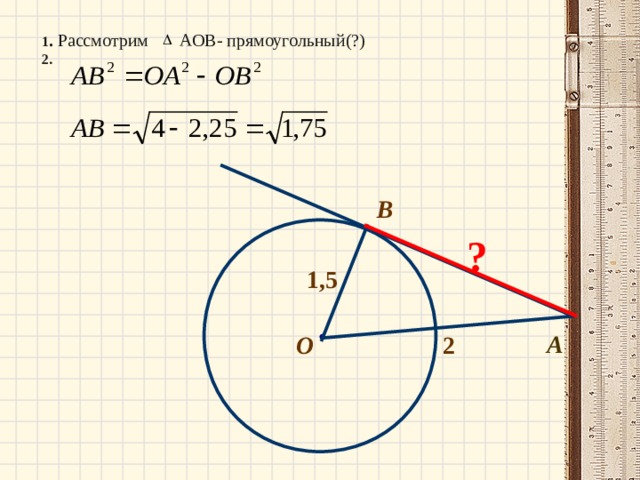
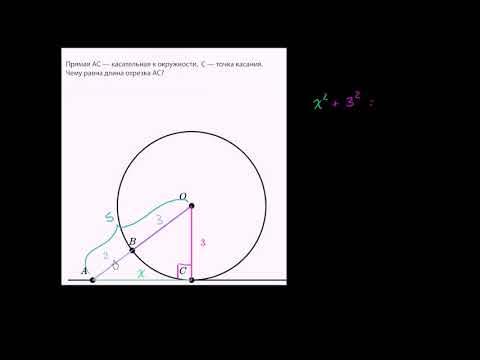
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.
Соединим отрезком точки O и B; полученный отрезок — радиус, проведённый в точку касания, поэтому OB перпендикулярен AB. Задача сводится к нахождению катета OB прямоугольного треугольника AOB. Из теоремы Пифагора:
В треугольнике ABC угол C равен 90°, AC = 30 , BC = 
Найдите радиус окружности, описанной около этого треугольника.
Вписанный прямой угол опирается на диаметр окружности, поэтому радиус окружности, описанной вокруг прямоугольного треугольника, равен половине гипотенузы. По теореме Пифагора имеем:
Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
Проведём построение и введём обозначения, как показано на рисунке. Рассмотрим треугольники AOH и HOB, они прямоугольные, OH — общая, AO и OB равны как радиусы окружности, следовательно, эти треугольники равны, откуда 
По теореме Пифагора найдём радиус окружности:
Диаметр равен двум радиусам, следовательно, 
- Касательная к окружности. Решение задач
- Просмотр содержимого документа «Касательная к окружности. Решение задач»
- Геометрия 8 класс. Задачи по теме: Касательная к окружности
- Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 📽️ Видео
Видео:8 класс, 32 урок, Касательная к окружностиСкачать
Касательная к окружности. Решение задач
Просмотр содержимого документа
«Касательная к окружности. Решение задач»
8 класс. Геометрия
Решение задач по теме «Касательная к окружности»
Учитель математики: Барсукова И.Е.
Повторение теоретического материала
Как вы думаете, сколько общих точек могут иметь прямая и окружность?
r две общие точки одна общая точка не имеют общих точек Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку . Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки . Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек . » width=»640″
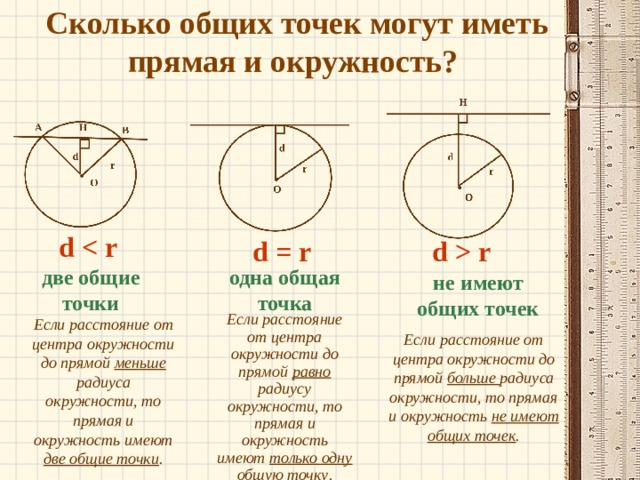
Сколько общих точек могут иметь прямая и окружность?
две общие точки
одна общая точка
не имеют общих точек
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку .
Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки .
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек .
Касательная к окружности
Определение: П рямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
m – касательная к окружности с центром О
М – точка касания
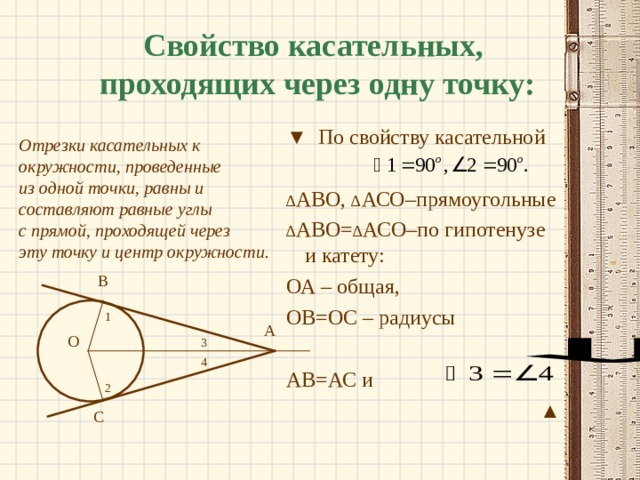
Свойство касательных, проходящих через одну точку:
Отрезки касательных к
из одной точки, равны и
составляют равные углы
с прямой, проходящей через
эту точку и центр окружности.
▼ По свойству касательной
∆ АВО= ∆ АСО–по гипотенузе и катету:
Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она является к асательной.
окружность с центром О
m – прямая, которая проходит через точку М
1 . Рассмотрим АОВ- прямоугольный(?)
Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать
Геометрия 8 класс. Задачи по теме: Касательная к окружности
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Геометрии 8 класс. Задачи по теме: Касательная к окружности.
Длина хорды окружности равна 48, а расстояние от центра окружности до этой хорды равно 70. Найдите диаметр окружности.
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=12см, AO=13см.
На отрезке AB выбрана точка C так, что АС=14, ВС=36. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 75°. Найдите величину угла OMK. Ответ дайте в градусах.
Отрезок АВ=48 касается окружности радиуса 14 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
В угол C величиной 79° вписана окружность, которая касается сторон угла в точках A и B, точка O – центр окружности. Найдите угол AOB. Ответ дайте в градусах.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 6.
Длина хорды окружности равна 30, а расстояние от центра окружности до этой хорды равно 36. Найдите диаметр окружности.
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если см, AB=40см, AO=85см.
На отрезке AB выбрана точка C так, что АС=6, ВС=4. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 54°. Найдите величину угла OMK. Ответ дайте в градусах.
Отрезок АВ=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B, точка O – центр окружности. Найдите угол AOB. Ответ дайте в градусах.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 942 человека из 79 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 677 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 302 человека из 68 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать
Дистанционные курсы для педагогов
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 513 064 материала в базе
Материал подходит для УМК
«Геометрия. 7-9 класс», Волович М.Б., Атанасян Л.С.
§ 16. Касательная к окружности
Другие материалы
- 15.03.2020
- 199
- 0
- 15.03.2020
- 238
- 1
- 14.03.2020
- 234
- 4
- 13.03.2020
- 172
- 0
- 12.03.2020
- 126
- 0
- 12.03.2020
- 1772
- 99
- 11.03.2020
- 227
- 0
- 10.03.2020
- 471
- 2
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 18.03.2020 5490
- DOCX 130.1 кбайт
- 322 скачивания
- Рейтинг: 2 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Корякова Надежда Вячеславовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 4 месяца
- Подписчики: 2
- Всего просмотров: 6764
- Всего материалов: 3
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Урок по теме КАСАТЕЛЬНАЯ К ОКРУЖНОСТИСкачать
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
В Петербурге открыли памятник работавшим во время блокады учителям
Время чтения: 1 минута
Школы Сургута переведут на дистанционное обучение с 24 января
Время чтения: 1 минута
Студенты РФ и Великобритании подписали договор о создании студенческой Ассоциации
Время чтения: 1 минута
Онлайн-семинар о снятии эмоционального напряжения у детей и подростков
Время чтения: 2 минуты
В России утвердили новые правила аккредитации образовательных учреждений
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
📽️ Видео
Геометрия 8 класс: Решение задач на касательную к окружностиСкачать
КАСАТЕЛЬНАЯ к ОКРУЖНОСТИ 8 класс геометрия АтанасянСкачать
КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ в точке ЗАДАЧИ 8 классСкачать
Касательные к окружности | Задачи 11-20 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать
Касательные к окружности пересекаются в точке. Теорема и решение задач. Геометрия 7-8 классСкачать
8 класс геометрия Касательная к окружности Решение задачСкачать
Геометрия 8 класс : Касательная к окружностиСкачать
НЕКОТОРЫЕ СВОЙСТВА ОКРУЖНОСТИ. КАСАТЕЛЬНАЯ к окружности. §20 геометрия 7 классСкачать
Решение задач Касательная к окружностиСкачать
Касательная к окружности | Геометрия 7-9 класс #69 | ИнфоурокСкачать
71. Касательная к окружностиСкачать
Задачи с касательными к окружности. Пример 3. | Окружность | ГеометрияСкачать
Геометрия 8 класс. Касательная к окружностиСкачать
Касательная к окружностиСкачать
Задачи с касательными к окружности. Пример 1. | Окружность | ГеометрияСкачать
