О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Доказательство теоремы синусов
- Доказательство следствия из теоремы синусов
- Теорема о вписанном в окружность угле
- Примеры решения задач
- Запоминаем
- Описанные и вписанные окружности — формулы, свойства и определение с примерами решения
- Описанная и вписанная окружности треугольника
- Прямоугольный треугольник и его описанная и вписанная окружности
- Вписанные и описанные четырехугольники
- Окружность, вписанная в треугольник
- Описанная трапеция
- Дополнительные свойства и признаки вписанного четырехугольника
- Обобщенная теорема Пифагора
- Формула Эйлера для окружностей
- Справочная информация по описанной и вписанной окружности треугольника
- Планиметрия. Страница 3
- 1.Окружность
- 2.Окружность, описанная около треугольника
- 3.Окружность, вписанная в треугольник
- 4.Геометрическое место точек
- Репетитор: Васильев Алексей Александрович
- Пример 1
- Пример 2
- Пример 3
- Пример 4
- Пример 5
- 🌟 Видео
Видео:Геометрия Найдите диаметр окружности, описанной около прямоугольного треугольника, если один из егоСкачать

Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
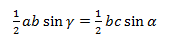
На b сокращаем, синусы переносим в знаменатели:
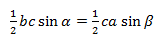
bc sinα = ca sinβ
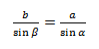
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
- Стороны треугольника, если даны два угла и одна сторона.
- Углы треугольника, если даны две стороны и один прилежащий угол.
Видео:Как найти диаметр окружности, описанной около равнобедренного треугольникаСкачать

Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
- sin120° = sin(180° — 60°) = sin60° = 3/√2;
- sin150° = sin(180° — 30°) = sin30° = 1/2;
- sin135° = sin(180° — 45°) = sin45° = 2/√2.
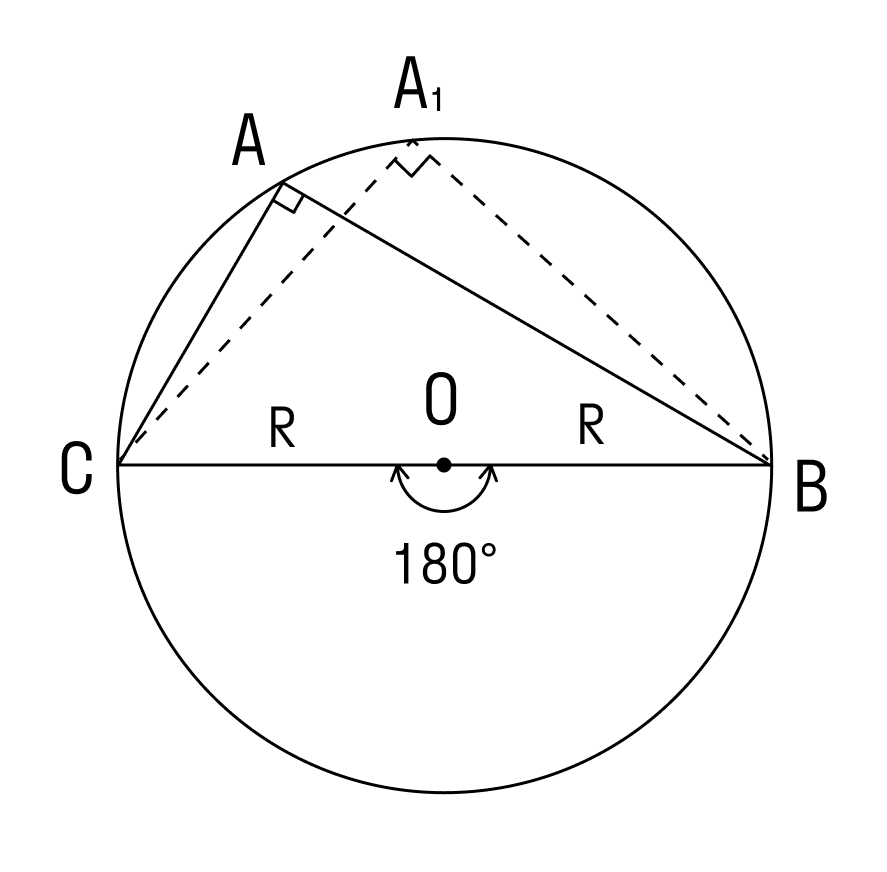
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Видео:Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
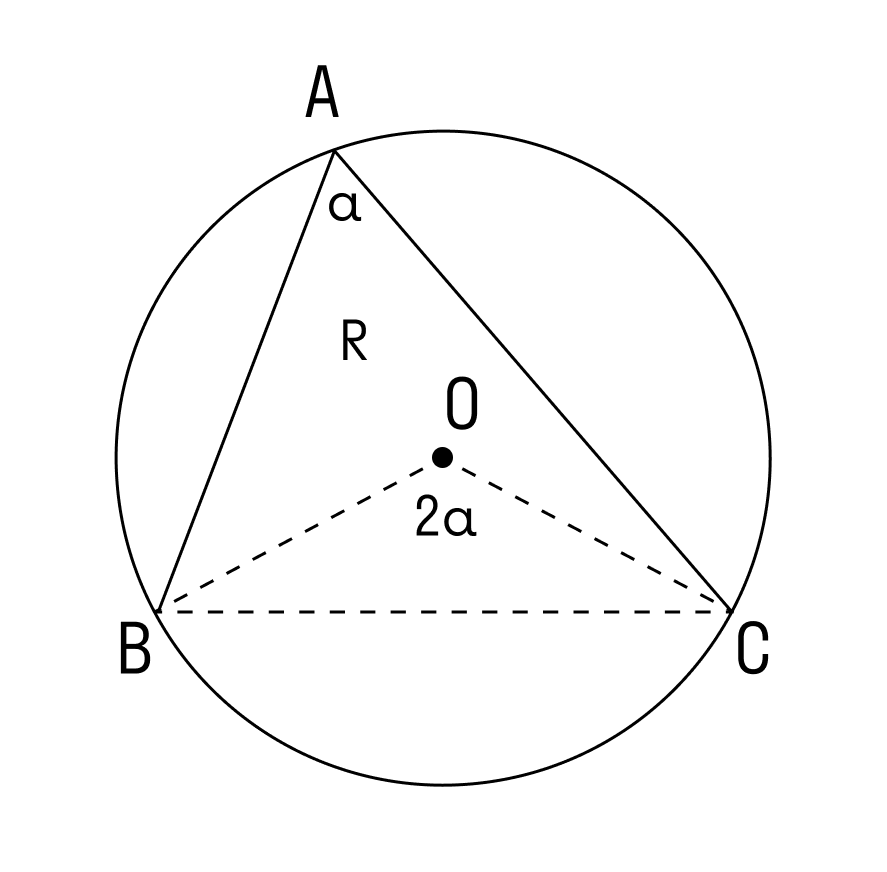
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
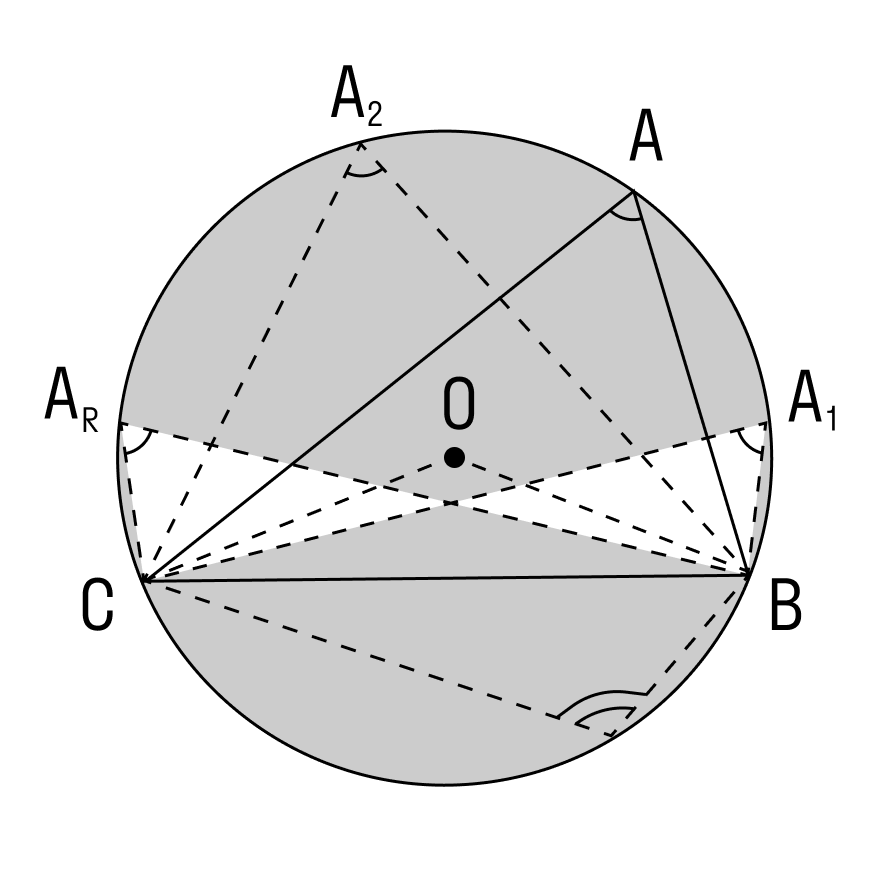
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
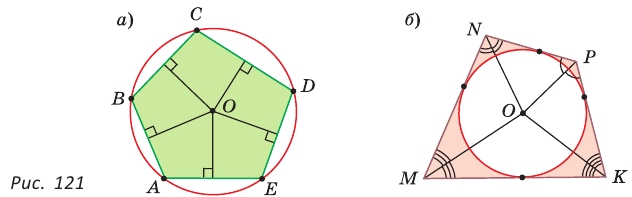
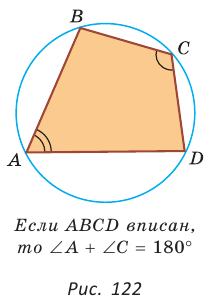
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° — α)
Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα
Видео:Нахождение диаметра описанной окружностиСкачать
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
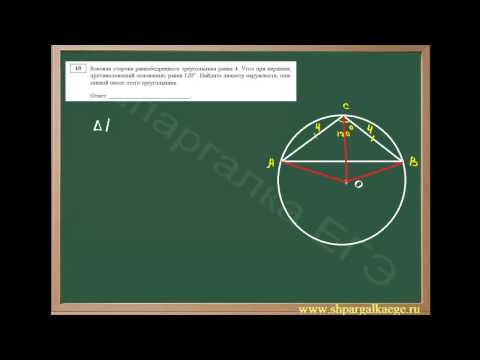
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
- Согласно теореме о сумме углов треугольника:
∠B = 180° — 45° — 15° = 120°
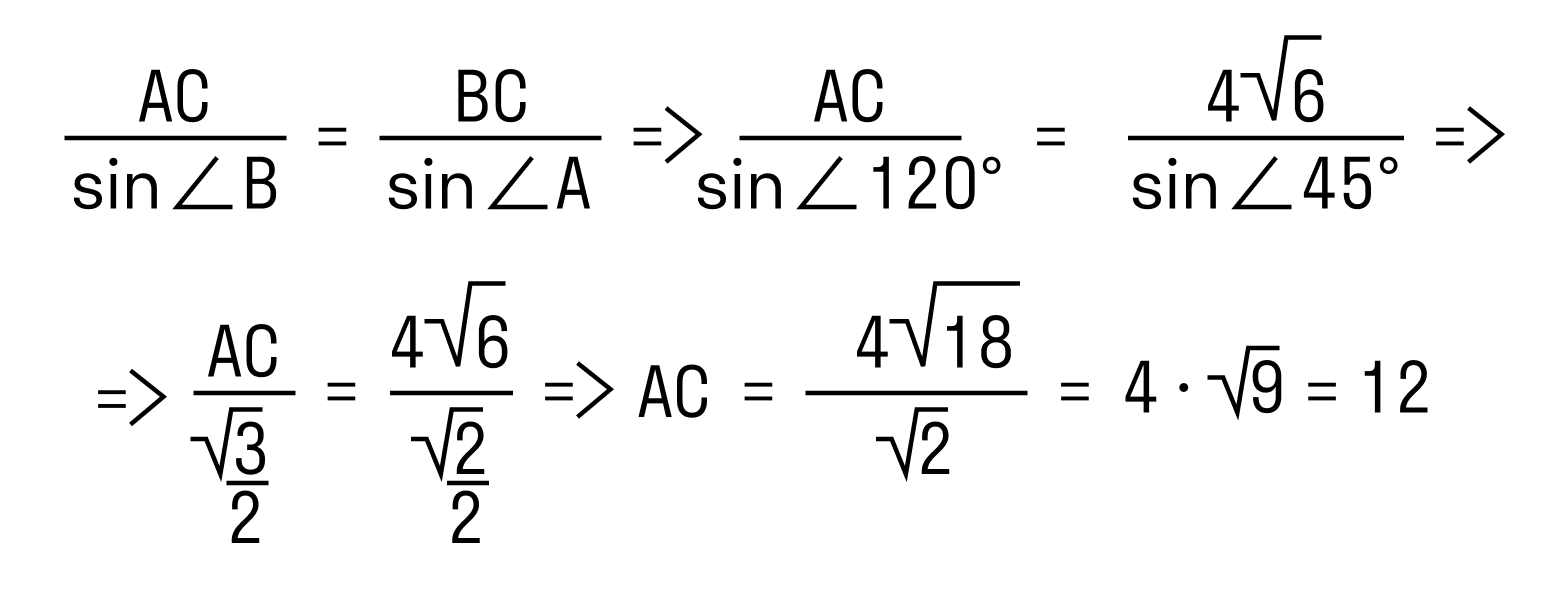
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Плоские и пространственные фигуры
- Взаимное расположение точек и прямых
- Сравнение и измерение отрезков и углов
- Первый признак равенства треугольников
- Треугольники и окружность
- Площадь треугольника
- Соотношения между сторонами и углами произвольного треугольника
- Окружность и круг
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Планиметрия. Страница 3

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

1.Окружность
Окружностью называется фигура, состоящая из множества точек на плоскости, равноудаленных от данной точки.
Эта данная точка называется центром окружности. Расстояние от центра окружности до ее точек называется радиусом окружности.
Отрезок, соединяющий две точки окружности, называется хордой.
Если хорда проходит через центр окружности, то она называется диаметром. (Рис.1)
ОА — радиус
ВС — диаметр
DE — хорда
Рис.1 Окружность, радиус, диаметр, хорда.
Видео:ЕГЭ 6 номер. Нахождение диаметра описанной окружности около равнобедренного треугольникаСкачать

2.Окружность, описанная около треугольника
Теорема: центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров, опущенных на середины сторон данного треугольника.
Доказательство. Пусть АВС данный треугольник и точка О является центром окружности, описанной около данного треугольника. (Рис.2) Тогда отрезки ОА, ОВ, ОС равны как радиусы. Следовательно, треугольники Δ АОВ, Δ ВОС, Δ АОС — равнобедренные. А следовательно, и медианы, проведенные к серединам сторон ОК, ОЕ, ОD, являются одновременно биссектрисой и высотой. Поэтому предположение, что центр окружности, описанной около треугольника, является точкой пересечения высот, верно.
Рис.2 Теорема. Окружность, описанная около треугольника.
Видео:Радиус и диаметрСкачать

3.Окружность, вписанная в треугольник
Теорема. центр окружности, вписанной в треугольник, является точкой пересечения биссектрис, проведенных из его углов.
Доказательство. Пусть дан треугольник АВС. Точка О — центр вписанной окружности. (Рис. 3)
Тогда треугольник Δ АОЕ равен треугольнику Δ АОТ,
Δ СОЕ = Δ СОК,
Δ ВОК = Δ ВОТ.
Так как стороны ОА, ОВ, ОС у них общие. А ОК, ОЕ, ОТ как радиусы.
Следовательно:
∠ ЕАО = ∠ ТАО,
∠ ЕСО = ∠ КСО,
∠ КВО = ∠ ТВО.
Это значит, что точка О лежит на пересечении биссектрис АО, ВО, СО.

Рис.3 Теорема. Окружность, вписанная в треугольник.
Видео:Свойство окружности, описанной около равнобедренного треугольникаСкачать

4.Геометрическое место точек
Геометрическое место точек это фигура, которая представляет собой совокупность точек на плоскости, подчиняющихся определенному закону или обладающих определенным свойством.
Теорема. Геометрическим местом точек называется прямая, все точки которой равноудалены от двух данных точек, перпендикулярная отрезку, соединяющему эти точки и проходящая через его середину.
Доказательство. Пусть дан отрезок АС. Прямая А проходит через середину этого отрезка и перпендикулярна ему.(Рис. 4).
Тогда треугольники Δ АМВ и Δ СМВ равны. Так как сторона ВМ у них обшая, а стороны АМ и МС равны по условию. Следовательно точка В равноудалена от точек А и С.
Возьмем другую точку, например D, не лежащую на прямой а. Тогда сторона MD не принадлежит прямой а. А следовательно, углы AMD и DMC не равны т.к. не равны треугольники. Данное утверждение основано на том, что через точку, лежащую на прямой, можно провести только одну перпендикулярную ей прямую. И следовательно, расстояния от точки D до точек А и С не равны. Поэтому, для того чтобы расстояния от некой точки Х до двух данных точек были равны, необходимо чтобы она лежала на прямой а, которая перпендикулярна отрезку, соединяющего эти точки, и которая проходит через его середину.

Рис.4 Теорема. Геометрическое место точек.
Репетитор: Васильев Алексей Александрович

Предметы: математика, физика, информатика, экономика, программирование.

Тел. 8 916 461-50-69, email: alexey-it@ya.ru

Пример 1
Дана окружность с центром О. И проведена касательная а из точки С к этой окружности. Доказать, что точка К лежит на основании равнобедренного треугольника ОВС, если OB = 2R. (рис.5)
По условию прямая а есть касательная к окружности, следовательно радиус, проведенный к точке касания ОК, и который лежит на прямой с, составляет прямой угол с касательной. Так как ОВ = 2R и KB = R, то прямая а будет представлять собой геометрическое место точек, так как она перпендикулярна отрезку ОВ и проходит через его середину. А следовательно, треугольники ВКС и ОКС равны по первому признаку равенства треугольников. Отсюда можно сделать вывод, что точка К будет лежать на основании равнобедренного треугольника ВОС.

Рис.5 Задача. Дана окружность с центром О.
Пример 2
Докажите, что касательная к окружности не имеет с ней других общих точек, кроме точки касания. (Рис.6)
Доказательство:
Пусть дана окружность с центром в точке О. И прямая а, которая касается окружности в точке А. Допустим, что прямая а имеет еще одну точку касаная — точку В. Тогда радиус окружности, проведенный к точкам А и В образует угол с прямой а равный 90°.
Таким образом, в равнобедренном треугольнике АОВ углы при вершинах А и В равны 90°. А это невозможно. Следовательно, мы пришли к противоречию и прямая а не может касаться окружности в двух точках.
Рис.6 Задача. Касательная к окружности.
Пример 3
Точки А,В,С лежат на одной прямой, а точка О лежит вне этой прямой. Докажите, что треугольники АОВ и ВОС не могут быть равнобедренными с основаниями АВ и ВС. (Рис.7)
Доказательство:
Допустим, что треугольники АОВ и ВОС равнобедренные с основаниями АВ и ВС. Тогда Стороны АО, ВО и СО равны. Отсюда следует, что углы ОАВ, АВО, ОВС и ОСВ равны. И ∠АВО = ∠ОВС = 90°, так как эти углы являются смежными, а их сумма равна 180°.
Таким образом, в равнобедренных треугольниках АОВ и ВОС углы при вершинах А и С равны 90°. А это невозможно, потому, что тогда стороны АО, ВО и СО были бы параллельны, так как они перпендикулярны одной прямой АС. Следовательно, мы пришли к противоречию, и треугольники АОВ и ВОС не могут быть равнобедренными с основаниями АВ и ВС.
Рис.7 Задача. Даны три точки на прямой.
Пример 4
Окружности с центрами О и О1 пересекаются в точках А и В. Докажите, что прямая АВ перпендикулярна прямой ОО1 (Рис.8)
Доказательство:
Так как окружности пересекаются в точках А и В, то эти две точки принадлежат обеим окружностям. Следовательно, отрезок ОА = ОВ, как радиусы окружности с центром в точке О. А отрезок О1А = О1В, как радиусы окружности с центром в точке О1.
Таким образом, треугольники ОАО1 и ОВО1 равны по третьему признаку равенства треугольников (по трем сторонам). А следовательно отрезки АС и ВС равны. И прямая ОО1 является геометрическим местом точек для двух данных точек А и В. Т.е. любая точка прямой ОО1 равноудалена от двух данных точек А и В. Следовательно, треугольники ОАС и ОВС равны, также как и треугольники АСО1 и ВСО1 по трем сторонам. А отсюда следует равенство углов при вершине С. Т.е. ∠ОСА = ∠ОСВ = ∠АСО1 = ∠ВСО1 = 90°.
Следовательно, можно сделать вывод, что прямая АВ перпендикулярна прямой ОО1.
Рис.8 Задача. Окружности с центрами О и О1.
Пример 5
Отрезок ВС пересекает прямую а в точке О. Расстояние от точек В и С до прямой а равны. Докажите, что точка О является серединой отрезка ВС (Рис.9)
Доказательство:
По условию задачи, расстояния от точек В и С до прямой а равны. Т.е. РС = BQ. Так как расстояние от точки до прямой представляет собой перпендикуляр, то два треугольника РОС и ВОQ, образованные двумя пересекающимися прямыми ВС и а, и перпендикулярами, опущенными на одну из них, равны по второму признаку равенства треугольников ( по стороне и двум прилегающим к ней углам: РС = BQ, углы при вершинах В и С равны как внутренние накрест лежащие, а углы при вершинах Р и Q прямые).
Из равенства треугольников РОС и ВОQ следует, что ВО = ОС.
Рис.9 Задача. Отрезок ВС пересекает прямую а .
🌟 Видео
Геометрия Сторона AD четырехугольника ABCD является диаметром окружности, описанной около негоСкачать

Задание 24 ОГЭ по математике #7Скачать

№707. Угол, противолежащий основанию равнобедренного треугольника, равен 120°, боковая сторонаСкачать

ОГЭ Задание 16 Описанная окружность ДиаметрСкачать

Геометрия. ОГЭ по математике. Задание 16Скачать

ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

№702. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углыСкачать



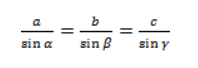
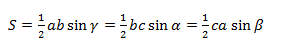
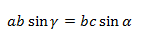
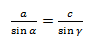
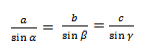

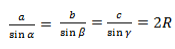

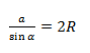


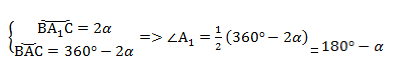

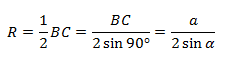
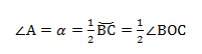
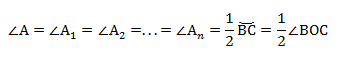
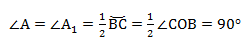

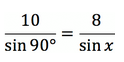
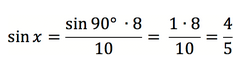


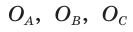
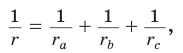 где
где 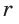 — радиус вписанной окружности треугольника,
— радиус вписанной окружности треугольника,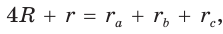 где R — радиус описанной окружности
где R — радиус описанной окружности 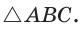
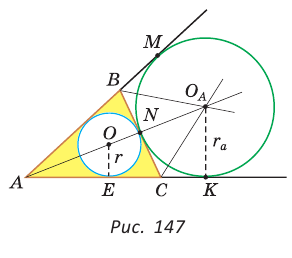
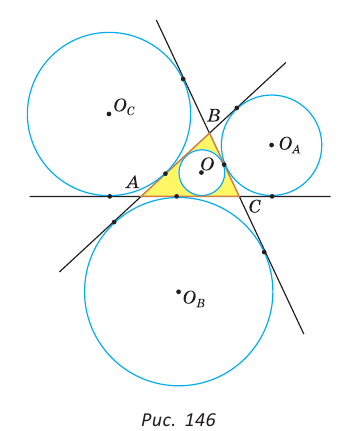
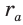 вневписанной окружности треугольника АВС со сторонами а, b и с (рис. 147). Для этого проведем радиусы
вневписанной окружности треугольника АВС со сторонами а, b и с (рис. 147). Для этого проведем радиусы 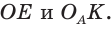 По свойству касательной
По свойству касательной 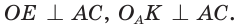 Из подобия прямоугольных треугольников АОЕ и
Из подобия прямоугольных треугольников АОЕ и 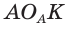 (по острому углу) следует
(по острому углу) следует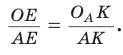 Так как
Так как 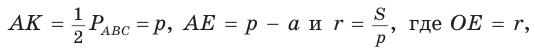 то
то 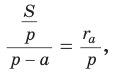 откуда
откуда 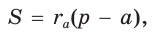
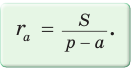
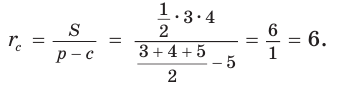

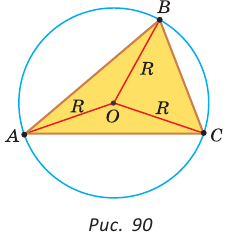
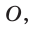 описанная около треугольни ка АВС.
описанная около треугольни ка АВС.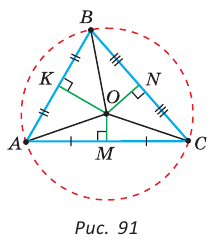
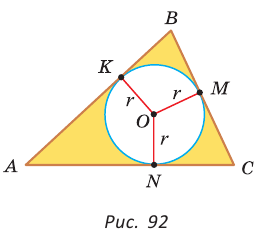
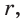 вписанная в треугольник АВС; К, М и N — точки ее касания со сторонами треугольника АВС.
вписанная в треугольник АВС; К, М и N — точки ее касания со сторонами треугольника АВС. 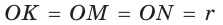 и по свойству касательной к окружности
и по свойству касательной к окружности 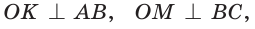
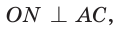 то центр вписанной окружности равноудален от сторон треугольника.
то центр вписанной окружности равноудален от сторон треугольника.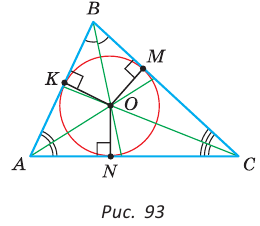
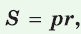 где
где 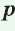 — полупериметр треугольника,
— полупериметр треугольника, 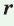 — радиус окружности, вписанной в этот треугольник.
— радиус окружности, вписанной в этот треугольник.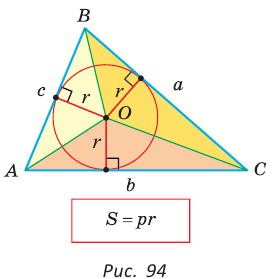
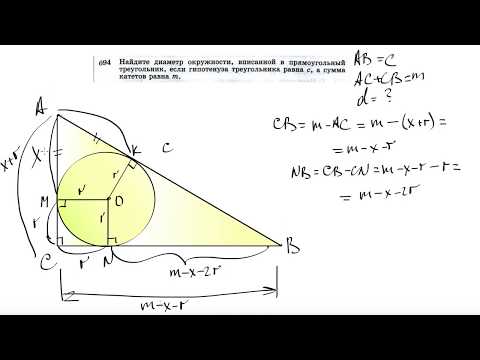
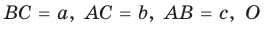 — центр его вписанной окружности (рис. 94). Соединим отрезками точку О с вершинами А, В и С. Треугольник АВС разобьется на три треугольника:
— центр его вписанной окружности (рис. 94). Соединим отрезками точку О с вершинами А, В и С. Треугольник АВС разобьется на три треугольника: 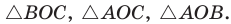 Радиусы
Радиусы 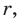 проведенные в точки касания, будут высотами этих треугольников. Площадь треугольника АВС равна сумме площадей указанных треугольников:
проведенные в точки касания, будут высотами этих треугольников. Площадь треугольника АВС равна сумме площадей указанных треугольников: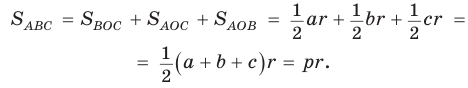
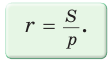
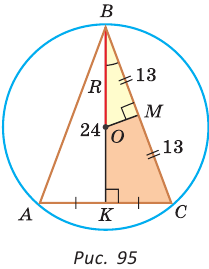
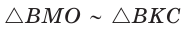 (как прямоугольные с общим острым углом СВК), то ,
(как прямоугольные с общим острым углом СВК), то , 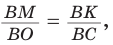
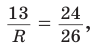 откуда
откуда 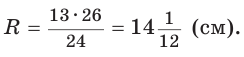
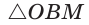 (см. рис. 95)
(см. рис. 95) 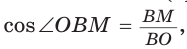 из
из 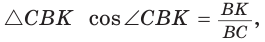 откуда
откуда 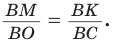 Дальнейшее решение совпадает с приведенным в способе 1.
Дальнейшее решение совпадает с приведенным в способе 1.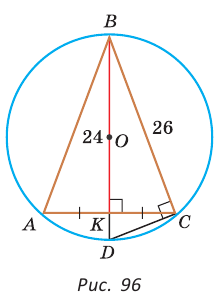
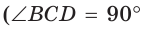 как вписанный, опирающийся на диаметр) катет ВС есть среднее пропорциональное между гипотенузой BD и проекцией ВК катета ВС на гипотенузу. Поэтому
как вписанный, опирающийся на диаметр) катет ВС есть среднее пропорциональное между гипотенузой BD и проекцией ВК катета ВС на гипотенузу. Поэтому 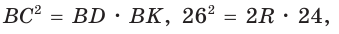 откуда
откуда 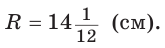
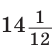 см.
см. 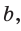 а высоту, проведенную к основанию, —
а высоту, проведенную к основанию, — 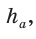 то получится пропорция
то получится пропорция 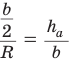 .
. 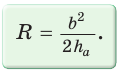
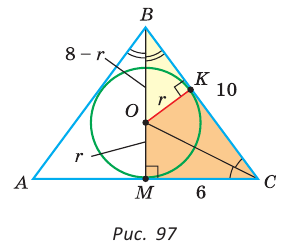
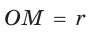 — искомый радиус вписанной окружности. Так как AM = МС = 6 см, то из
— искомый радиус вписанной окружности. Так как AM = МС = 6 см, то из 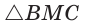 по теореме Пифагора
по теореме Пифагора 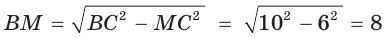 (см), откуда
(см), откуда 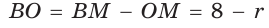 (см). Проведем радиус ОК в точку касания окружности со стороной
(см). Проведем радиус ОК в точку касания окружности со стороной 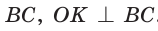 . Из подобия прямоугольных треугольников ВКО и ВМС (
. Из подобия прямоугольных треугольников ВКО и ВМС ( 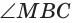 — общий) следует:
— общий) следует: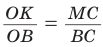 . Тогда
. Тогда 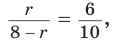
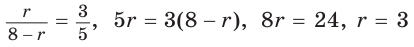 (см).
(см). 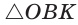 (см. рис. 97)
(см. рис. 97) 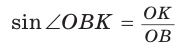 , из
, из 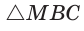
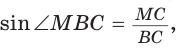 откуда
откуда 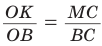 . Дальнейшее решение совпадает с приведенным в способе 1.
. Дальнейшее решение совпадает с приведенным в способе 1.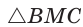 . Известно, что биссектриса треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам. Поэтому
. Известно, что биссектриса треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам. Поэтому 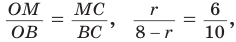 ‘ откуда
‘ откуда 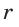 = 3 (см).
= 3 (см).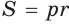 ).
). 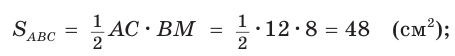
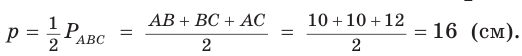 Из формулы площади треугольника
Из формулы площади треугольника 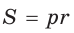 следует:
следует: 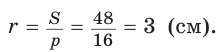
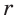 его вписанной окружности.
его вписанной окружности.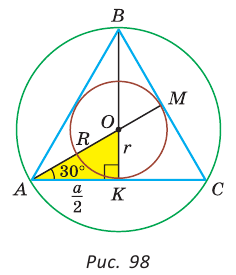
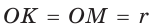 — радиусы вписанной окружности. Так как AM — биссектриса и
— радиусы вписанной окружности. Так как AM — биссектриса и 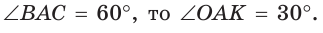 Поскольку ВК — высота и медиана, то
Поскольку ВК — высота и медиана, то 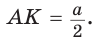 Из
Из 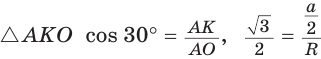 , откуда
, откуда 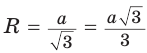 .
. 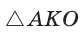 катет ОК лежит против угла в 30°, поэтому
катет ОК лежит против угла в 30°, поэтому 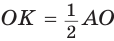 ,
, 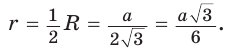
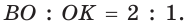 Высоту равностороннего треугольника можно найти по формуле
Высоту равностороннего треугольника можно найти по формуле 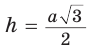 . Откуда
. Откуда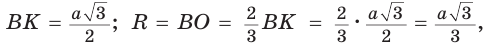
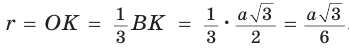
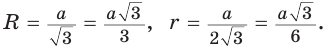
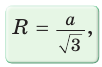 то
то 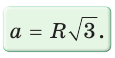 Значит, сторона равностороннего
Значит, сторона равностороннего 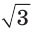 раз больше радиуса его описанной окружности.
раз больше радиуса его описанной окружности. 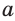 разделить на
разделить на 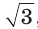 , а чтобы найти его сторону а, нужно радиус R умножить на
, а чтобы найти его сторону а, нужно радиус R умножить на 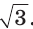 . Радиус вписанной окружности равностороннего треугольника
. Радиус вписанной окружности равностороннего треугольника 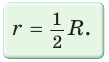
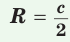 где с — гипотенуза.
где с — гипотенуза.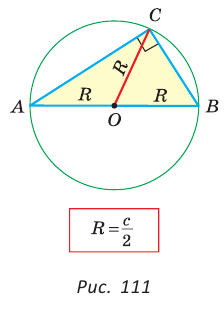
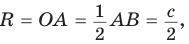 где с — гипотенуза.
где с — гипотенуза. 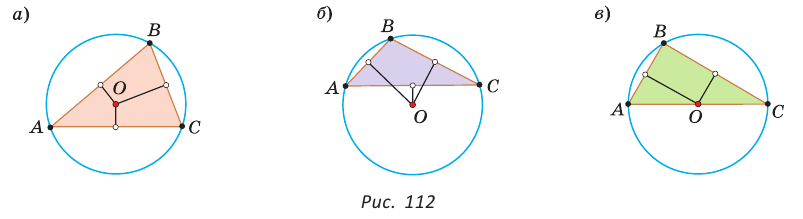
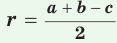 , где
, где 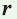 — искомый радиус,
— искомый радиус, 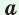 и
и 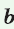 — катеты,
— катеты, 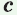 — гипотенуза треугольника.
— гипотенуза треугольника.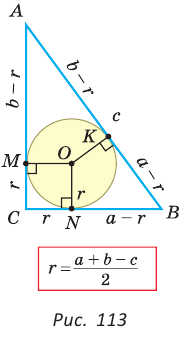
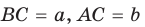 и гипотенузой
и гипотенузой 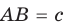 . Пусть вписанная в треугольник окружность с центром О и радиусом
. Пусть вписанная в треугольник окружность с центром О и радиусом 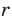 касается сторон треугольника в точках М, N и К (рис. 113).
касается сторон треугольника в точках М, N и К (рис. 113). 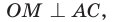
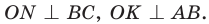 Четырехугольник CMON — квадрат, так как у него все углы прямые и
Четырехугольник CMON — квадрат, так как у него все углы прямые и 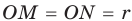 . Тогда
. Тогда 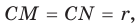
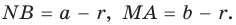 Так как отрезки касательных, проведенных из одной точки к окружности, равны между собой, то
Так как отрезки касательных, проведенных из одной точки к окружности, равны между собой, то 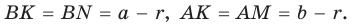 Но
Но 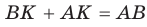 , т. е.
, т. е. 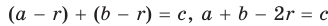 , откуда
, откуда 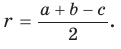
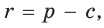 где р — полупериметр треугольника.
где р — полупериметр треугольника.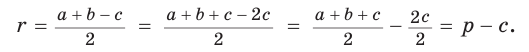
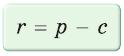 в сочетании с формулами
в сочетании с формулами 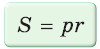 и
и 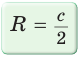 дает возможность решать многие задачи, связанные с прямоугольным треугольником, алгебраическим методом.
дает возможность решать многие задачи, связанные с прямоугольным треугольником, алгебраическим методом.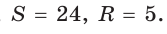 Найти
Найти 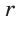 .
.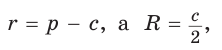 то
то 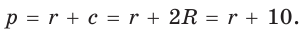
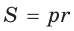 следует
следует 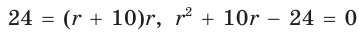 . По теореме Виета (обратной)
. По теореме Виета (обратной) 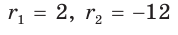 — посторонний корень.
— посторонний корень. 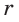 = 2.
= 2.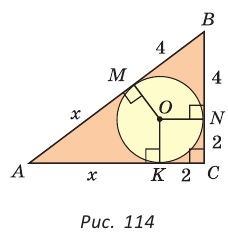
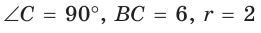 — радиус вписанной окружности (рис. 114). Проведем из центра О вписанной окружности перпендикуляры ОК, ОМ и ON к сторонам треугольника, которые будут радиусами вписанной окружности. Так как
— радиус вписанной окружности (рис. 114). Проведем из центра О вписанной окружности перпендикуляры ОК, ОМ и ON к сторонам треугольника, которые будут радиусами вписанной окружности. Так как 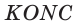 — квадрат, то
— квадрат, то 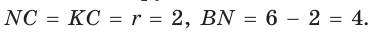
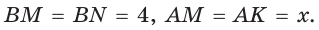
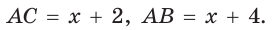 По теореме Пифагора
По теореме Пифагора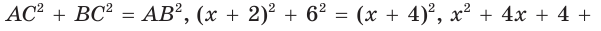
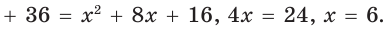
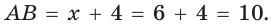
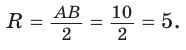
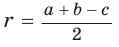 значения
значения 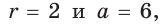 получим
получим 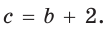 По теореме Пифагора
По теореме Пифагора 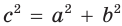 , т. е.
, т. е. 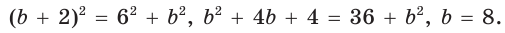 Тогда
Тогда 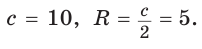
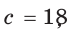 радиус вписанной в него окружности
радиус вписанной в него окружности 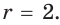 Найти площадь треугольника.
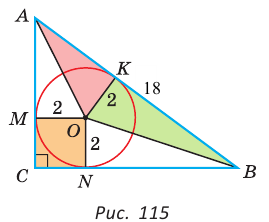
Найти площадь треугольника.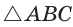 гипотенуза АВ — = с = 18,0 — центр вписанной окружности, ОК, ОМ, ON — ее радиусы, проведенные в точки касания (рис. 115). Так как
гипотенуза АВ — = с = 18,0 — центр вписанной окружности, ОК, ОМ, ON — ее радиусы, проведенные в точки касания (рис. 115). Так как 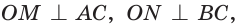
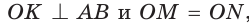 , то CMON — квадрат co стороной, равной радиусу
, то CMON — квадрат co стороной, равной радиусу 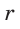 вписанной окружности,
вписанной окружности, 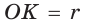 — высота
— высота  . Поскольку отрезки касательных, проведенных из одной точки к окружности, равны между собой, то АК = AM, ВК = BN.
. Поскольку отрезки касательных, проведенных из одной точки к окружности, равны между собой, то АК = AM, ВК = BN. 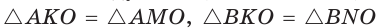 по катету и гипотенузе.
по катету и гипотенузе.  равна сумме удвоенной площади
равна сумме удвоенной площади  и площади квадрата CMON, т. е.
и площади квадрата CMON, т. е.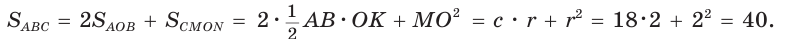
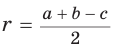 следует
следует 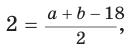
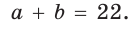 Возведем части равенства в квадрат:
Возведем части равенства в квадрат: 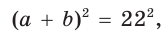
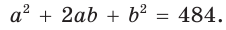 Так как
Так как 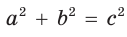 и
и 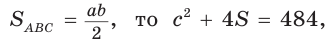
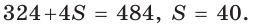
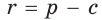 следует, что
следует, что 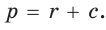 Из формулы
Из формулы 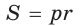 следует, что
следует, что 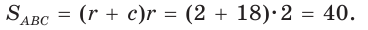

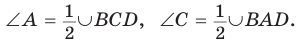 Дуги BCD и BAD дополняют друг друга до окружности, и поэтому сумма их градусных мер равна 360°. Отсюда
Дуги BCD и BAD дополняют друг друга до окружности, и поэтому сумма их градусных мер равна 360°. Отсюда 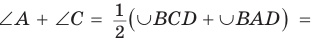
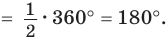 Аналогично доказывается, что
Аналогично доказывается, что 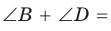 180°. Теорема доказана.
180°. Теорема доказана. то около него можно описать окружность.
то около него можно описать окружность.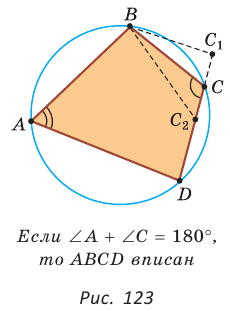
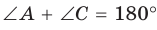 (рис. 123). Через вершины А, В и D проведем окружность (около любого треугольника можно описать окружность). Если бы вершина С не лежала на данной окружности, а находилась вне ее в положении
(рис. 123). Через вершины А, В и D проведем окружность (около любого треугольника можно описать окружность). Если бы вершина С не лежала на данной окружности, а находилась вне ее в положении 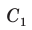 или внутри нее в положении
или внутри нее в положении 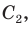 то в первом случае угол С был бы меньше, а во втором — больше половины градусной меры дуги BAD (по свойству угла между секущими и угла между пересекающимися хордами).
то в первом случае угол С был бы меньше, а во втором — больше половины градусной меры дуги BAD (по свойству угла между секущими и угла между пересекающимися хордами). 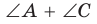 не была бы равна 180°. Следовательно, вершина С лежит на данной окружности. Теорема доказана.
не была бы равна 180°. Следовательно, вершина С лежит на данной окружности. Теорема доказана.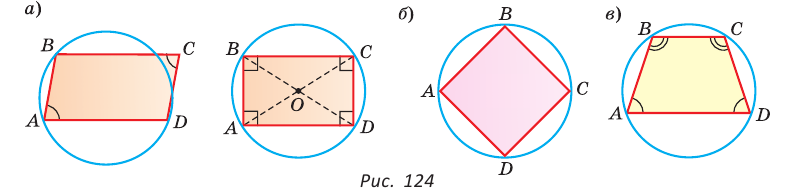
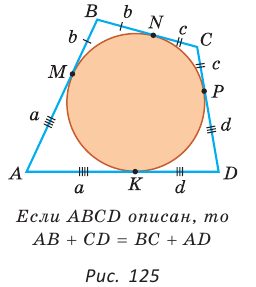
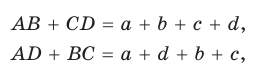
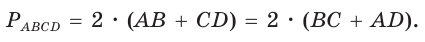
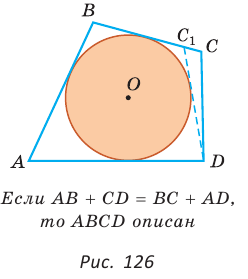
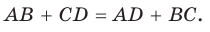 (1)
(1) 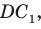 который касается окружности. По свойству описанного четырехугольника
который касается окружности. По свойству описанного четырехугольника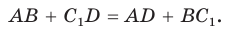 (2)
(2)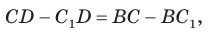
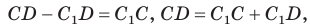 что противоречит неравенству треугольника.
что противоречит неравенству треугольника. 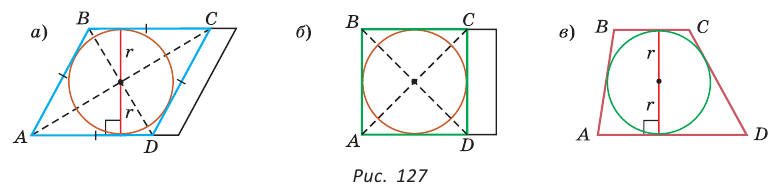
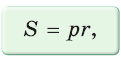 , где S — его площадь, р — полупериметр,
, где S — его площадь, р — полупериметр, 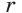 — радиус вписанной окружности.
— радиус вписанной окружности.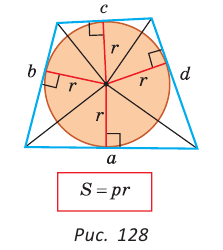
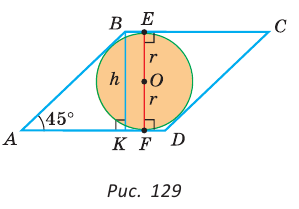
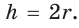 Так как у ромба все стороны равны , то
Так как у ромба все стороны равны , то 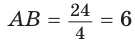 (см).
(см). 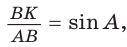 откуда
откуда 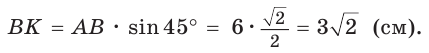 Искомый радиус вписанной окружности
Искомый радиус вписанной окружности 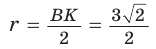 (см).
(см). 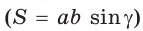 найдем площадь данного ромба:
найдем площадь данного ромба: 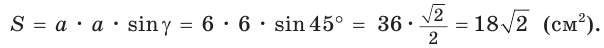 С другой стороны , площадь ромба можно найти по формуле площади описанного многоугольника
С другой стороны , площадь ромба можно найти по формуле площади описанного многоугольника 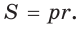 Поскольку
Поскольку 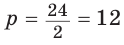 (см), то
(см), то 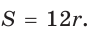 Отсюда
Отсюда 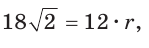
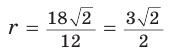 (см).
(см).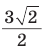 см.
см.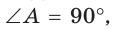 делит точкой касания большую боковую сторону CD на отрезки СК = 1, KD = 4. Найти площадь трапеции (рис. 130).
делит точкой касания большую боковую сторону CD на отрезки СК = 1, KD = 4. Найти площадь трапеции (рис. 130). 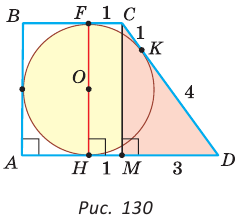
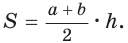 Необходимо найти сумму оснований и высоту трапеции. Проведем высоту
Необходимо найти сумму оснований и высоту трапеции. Проведем высоту 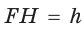 трапеции, проходящую через центр О вписанной окружности. По свойству касательных, проведенных из одной точки к окружности, CF = СК = 1, DH = DK = 4. Проведем высоту СМ. Так как HFCM — прямоугольник (все углы прямые), то НМ = FC = 1, MD = 3. В прямоугольном треугольнике CMD по теореме Пифагора
трапеции, проходящую через центр О вписанной окружности. По свойству касательных, проведенных из одной точки к окружности, CF = СК = 1, DH = DK = 4. Проведем высоту СМ. Так как HFCM — прямоугольник (все углы прямые), то НМ = FC = 1, MD = 3. В прямоугольном треугольнике CMD по теореме Пифагора 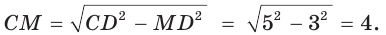 Тогда
Тогда 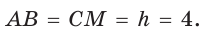 По свойству описанного четырехугольника
По свойству описанного четырехугольника 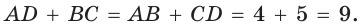 Отсюда
Отсюда 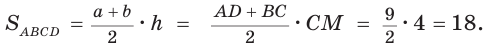
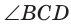 и
и 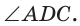 Так как
Так как 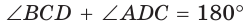 как внутренние односторонние углы при
как внутренние односторонние углы при 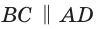 и секущей CD, то
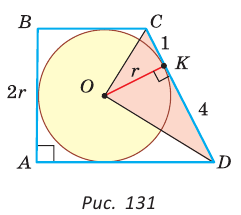
и секущей CD, то 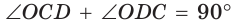 (рис. 131). Тогда
(рис. 131). Тогда 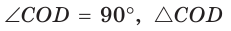 — прямоугольный, радиус
— прямоугольный, радиус 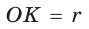 является его высотой, проведенной к гипотенузе CD. Высота прямоугольного треугольника, проведенная к гипотенузе, — есть среднее пропорциональное между проекциями катетов на гипотенузу. Поэтому
является его высотой, проведенной к гипотенузе CD. Высота прямоугольного треугольника, проведенная к гипотенузе, — есть среднее пропорциональное между проекциями катетов на гипотенузу. Поэтому 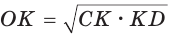 или
или 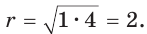 Высота
Высота 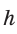 описанной трапеции равна диаметру вписанной окружности, откуда
описанной трапеции равна диаметру вписанной окружности, откуда 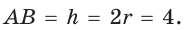 Так как по свойству описанного четырехугольника
Так как по свойству описанного четырехугольника 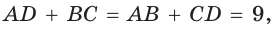 то
то 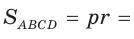
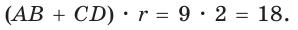
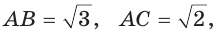
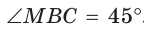 Найти величину угла ВАС (рис. 132, а).
Найти величину угла ВАС (рис. 132, а). 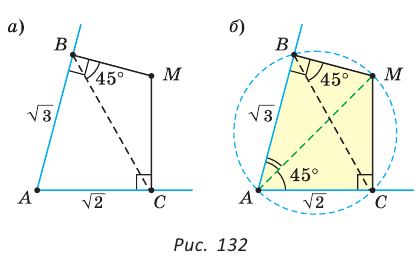
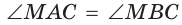 как вписанные углы, опирающиеся на одну и ту же дугу МС, то
как вписанные углы, опирающиеся на одну и ту же дугу МС, то 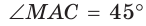 и прямоугольный треугольник АМС является равнобедренным,
и прямоугольный треугольник АМС является равнобедренным, 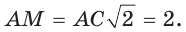 В прямоугольном треугольнике ABM
В прямоугольном треугольнике ABM 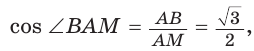 откуда
откуда 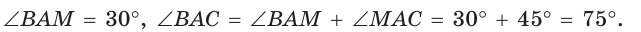
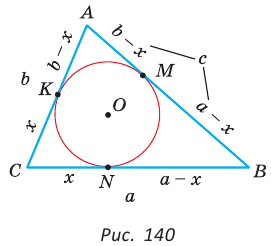
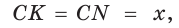 то
то 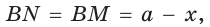
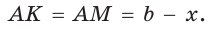 Так как АВ = AM + МВ, то
Так как АВ = AM + МВ, то 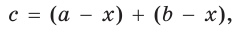 откуда
откуда 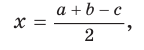 т. е.
т. е. 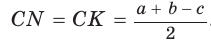 . После преобразований получим:
. После преобразований получим: 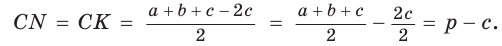 Аналогично:
Аналогично: 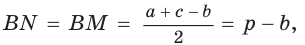
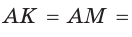
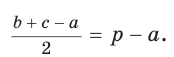
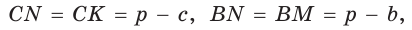
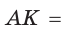
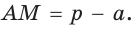
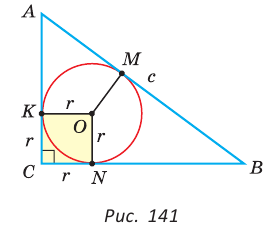
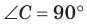 (рис. 141), то
(рис. 141), то 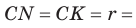
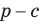 (см. c. 69). Формула радиуса окружности, вписанной в прямоугольный треугольник,
(см. c. 69). Формула радиуса окружности, вписанной в прямоугольный треугольник, 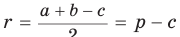 — частный случай результата задачи 1.
— частный случай результата задачи 1.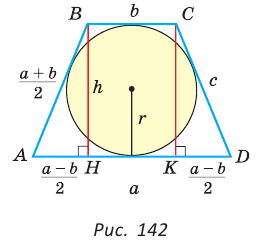
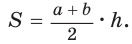 Пусть в трапеции ABCD основания
Пусть в трапеции ABCD основания 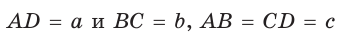 — боковые стороны,
— боковые стороны, 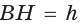 — высота (рис. 142). По свойству описанного четырехугольника АВ + CD = AD + ВС, откуда
— высота (рис. 142). По свойству описанного четырехугольника АВ + CD = AD + ВС, откуда 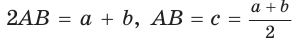 . Известно, что в равнобедренной трапеции
. Известно, что в равнобедренной трапеции 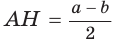 (можно опустить высоту СК и убедиться в этом). Из прямоугольного треугольника АНВ получаем:
(можно опустить высоту СК и убедиться в этом). Из прямоугольного треугольника АНВ получаем: 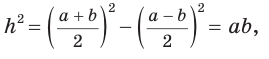
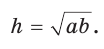 Отсюда
Отсюда 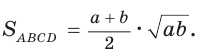 Ответ:
Ответ: 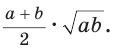
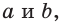 боковой стороной с, высотой h, средней линией
боковой стороной с, высотой h, средней линией 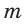 и радиусом
и радиусом 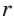 вписанной окружности (см. рис. 142) справедливы равенства:
вписанной окружности (см. рис. 142) справедливы равенства: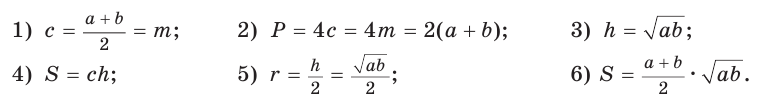
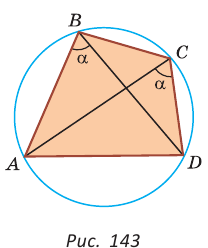
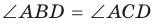 как вписанные углы, опирающиеся на одну и ту же дугу.
как вписанные углы, опирающиеся на одну и ту же дугу.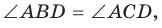 то около него можно описать окружность.
то около него можно описать окружность. 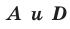 » . Данное свойство гарантирует, что вершины всех углов, равных углу ABD и лежащих по одну сторону от прямой AD, расположены на дуге ABD окружности. Поэтому окружность, описанная около треугольника ABD, пройдет и через вершину С. Теорема доказана.
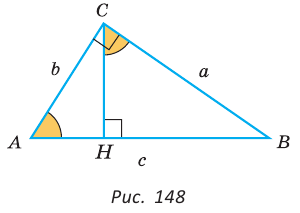
» . Данное свойство гарантирует, что вершины всех углов, равных углу ABD и лежащих по одну сторону от прямой AD, расположены на дуге ABD окружности. Поэтому окружность, описанная около треугольника ABD, пройдет и через вершину С. Теорема доказана.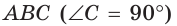 проведена высота СН, которая делит его на треугольники АСН и СВН, подобные между собой и подобные треугольнику
проведена высота СН, которая делит его на треугольники АСН и СВН, подобные между собой и подобные треугольнику 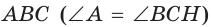 (рис. 148). Тогда теорема Пифагора
(рис. 148). Тогда теорема Пифагора 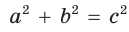 может звучать так: сумма квадратов гипотенуз
может звучать так: сумма квадратов гипотенуз 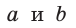 треугольников СВН и АСН равна квадрату гипотенузы треугольника АВС. И вообще, если
треугольников СВН и АСН равна квадрату гипотенузы треугольника АВС. И вообще, если 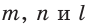 — соответствующие линейные элементы
— соответствующие линейные элементы 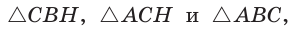 то можно сформулировать обобщенную теорему Пифагора:
то можно сформулировать обобщенную теорему Пифагора: 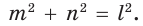
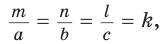 откуда
откуда 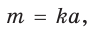
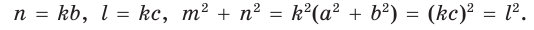
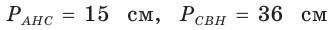 (см. рис. 148). Найдем
(см. рис. 148). Найдем 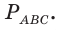 По обобщенной теореме Пифагора
По обобщенной теореме Пифагора 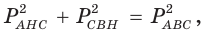 отсюда
отсюда 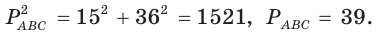
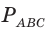 = 39.
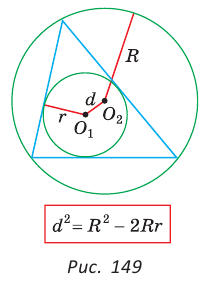
= 39.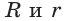 и расстоянием d между их центрами (рис. 149) справедлива формула Эйлера
и расстоянием d между их центрами (рис. 149) справедлива формула Эйлера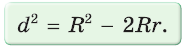
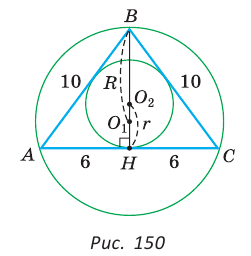
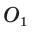 , и
, и 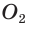 — лежат на прямой ВН (свойство равнобедренного треугольника). Тогда
— лежат на прямой ВН (свойство равнобедренного треугольника). Тогда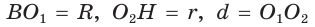 — расстояние между указанными центрами. Для нахождения радиуса описанной окружности воспользуемся формулой
— расстояние между указанными центрами. Для нахождения радиуса описанной окружности воспользуемся формулой 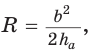 где b — боковая сторона,
где b — боковая сторона, 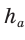 — высота, проведенная к основанию равнобедренного треугольника. Получим
— высота, проведенная к основанию равнобедренного треугольника. Получим 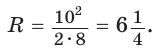 Радиус вписанной окружности
Радиус вписанной окружности 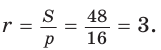 Так как
Так как 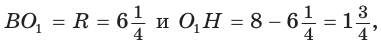 то
то 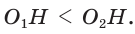 Искомое расстояние
Искомое расстояние 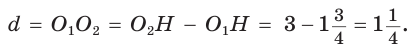
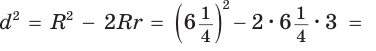
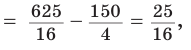 откуда
откуда 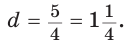 Как видим, формула Эйлера достаточно эффективна.
Как видим, формула Эйлера достаточно эффективна.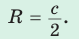
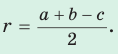
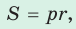 где
где 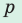 — полупериметр,
— полупериметр, 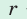 — радиус вписанной окружности.
— радиус вписанной окружности.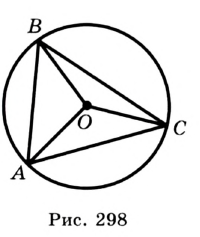
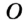 — центр окружности, описанной около треугольника
— центр окружности, описанной около треугольника 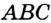 , поэтому
, поэтому 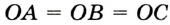 .
.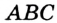 существует точка
существует точка 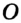 , равноудаленная от всех его вершин. Тогда точка
, равноудаленная от всех его вершин. Тогда точка 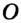 будет центром описанной окружности, а отрезки
будет центром описанной окружности, а отрезки 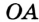 ,
, 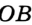 и
и 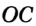 — ее радиусами.
— ее радиусами.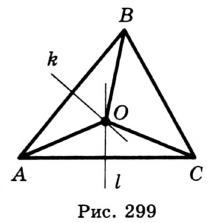
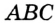 . Проведем серединные перпендикуляры
. Проведем серединные перпендикуляры 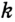 и
и 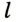 сторон
сторон 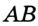 и
и 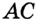 соответственно. Пусть точка
соответственно. Пусть точка 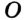 — точка пересечения этих прямых. Поскольку точка
— точка пересечения этих прямых. Поскольку точка  принадлежит серединному перпендикуляру
принадлежит серединному перпендикуляру 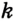 , то
, то 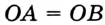 . Так как точка
. Так как точка 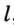 , то
, то 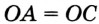 . Значит,
. Значит, 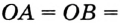
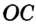 , т. е. точка
, т. е. точка 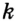 и
и 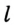 (рис. 299) имеют только одну точку пересечения. Следовательно, существует только одна точка, равноудаленная от всех вершин треугольника.
(рис. 299) имеют только одну точку пересечения. Следовательно, существует только одна точка, равноудаленная от всех вершин треугольника.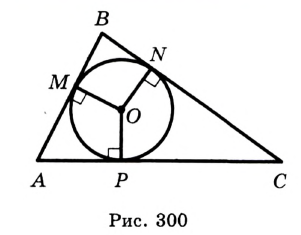
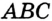 , отрезки
, отрезки 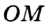 ,
, 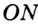 ,
, 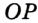 — радиусы, проведенные в точки касания,
— радиусы, проведенные в точки касания, 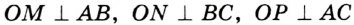 . Понятно, что центр вписанной окружности треугольника равноудален от всех его сторон.
. Понятно, что центр вписанной окружности треугольника равноудален от всех его сторон.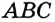 существует точка
существует точка 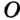 , удаленная от каждой его стороны на некоторое расстояние г. Тогда в силу следствия из теоремы 20.4 точка
, удаленная от каждой его стороны на некоторое расстояние г. Тогда в силу следствия из теоремы 20.4 точка 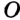 будет центром окружности радиуса г, которая касается сторон
будет центром окружности радиуса г, которая касается сторон 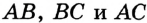 .
.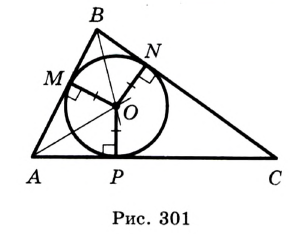
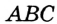 . Проведем биссектрисы углов
. Проведем биссектрисы углов  и
и  ,
, 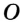 — точка их пересечения. Так как точка
— точка их пересечения. Так как точка  принадлежит биссектрисе угла
принадлежит биссектрисе угла 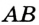 и
и 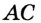 (теорема 19.2). Аналогично, так как точка
(теорема 19.2). Аналогично, так как точка 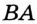 и
и 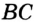 . Следовательно, точка
. Следовательно, точка 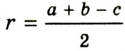 , где
, где 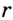 — радиус вписанной окружности,
— радиус вписанной окружности, 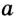 и
и 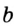 — катеты,
— катеты, 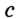 — гипотенуза.
— гипотенуза.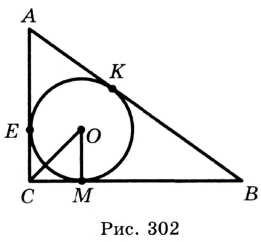
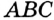 (рис. 302)
(рис. 302) 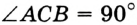 ,
, 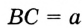 ,
, 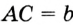 ,
, 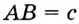 , точка
, точка 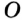 — центр вписанной окружности,
— центр вписанной окружности, 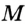 ,
, 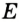 и
и 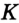 — точки касания вписанной окружности со сторонами
— точки касания вписанной окружности со сторонами 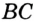 ,
, 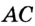 и
и 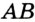 соответственно.
соответственно.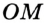 — радиус окружности, проведенный в точку касания. Тогда
— радиус окружности, проведенный в точку касания. Тогда 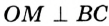 .
.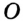 — центр вписанной окружности, то
— центр вписанной окружности, то 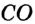 — биссектриса угла
— биссектриса угла 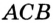 и
и 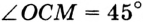 . Тогда
. Тогда 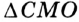 — равнобедренный прямоугольный,
— равнобедренный прямоугольный, 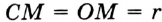 . Используя свойство отрезков касательных, проведенных к окружности из одной точки, получаем:
. Используя свойство отрезков касательных, проведенных к окружности из одной точки, получаем: