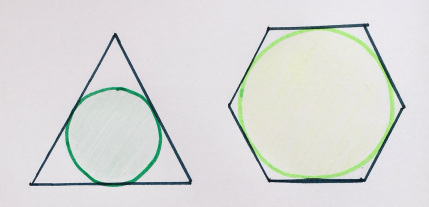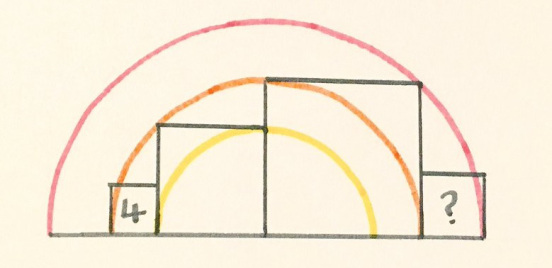- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Дистанционные курсы для педагогов
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Исследовательская работа «Круг в нашей жизни»
- Двадцать задачек (по безумной, восхитительной геометрии)
- 1. Сад часов
- 2. Опрокинутый квадрат
- 3. Это ловушка
- 4. Три квадратных тарелки
- 5. Красивая стрижка
- 6. Все люди рождены равными
- 7. Полукруг турдакен
- 8. Степенные хорды
- 9. Сказка о двух кругах
- 10. Doc Oct
- 11. Всё в квадрате
- 12. Шип в улье
- 13. Я видел равнобедренных
- 14. Зеленый против синего
- 15. Резцы по камню
- 16. Едем, едем, уехалиугольник
- 17. Только один факт
- 18. Стиральная машина
- 19. Летающие флаги
- 20. Тигрогон
- БОНУС:
- Закат над Квадратным городом
Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Дистанционные курсы для педагогов
Описание презентации по отдельным слайдам:
Длина окружности и площадь круга: Задачи из жизни
Длина окружности и площадь круга Π=3,1415926.. Примерное значение: Π= Π=3,14
Рассчитайте длину металлической полоски, чтобы обить колесо для телеги радиусом 30 см.
Рассчитайте количество плиток со стороной 10 см, необходимых для огораживания круглой клумбы радиусом 3 м.
Сколько пленки потребуется, чтобы накрыть сверху бассейн радиусом 3 м?
Сколько материи потребуется, чтобы сшить юбку-солнце (обрезки будут использованы для другого изделия)? R1= 100 см R2 = 10 см
Зрачок человеческого глаза в зависимости от степени яркости света изменяется в размере от 2 мм до 6 мм. Во сколько раз площадь расширенного зрачка больше площади суженного?
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 928 человек из 80 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 323 человека из 72 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 702 человека из 75 регионов
Ищем педагогов в команду «Инфоурок»
- Жданова Кира ВладимировнаНаписать 2963 26.01.2017
Номер материала: ДБ-136872
- 26.01.2017 2000
- 26.01.2017 266
- 26.01.2017 281
- 26.01.2017 353
- 26.01.2017 439
- 26.01.2017 540
- 26.01.2017 802
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Окружность. 7 класс.Скачать

Дистанционные курсы
для педагогов
530 курсов от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Стартовал региональный этап Всероссийской олимпиады школьников
Время чтения: 2 минуты
Первый мониторинг вузов РФ по новым показателям пройдёт в 2023 году
Время чтения: 2 минуты
В местах сдачи ЕГЭ будут применены антиковидные меры
Время чтения: 1 минута
Федеральный перечень учебников будет дополнен новыми учебниками
Время чтения: 3 минуты
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Планиметрия с окружностями | Задачи из ЕГЭ прошлых лет | №17 ЕГЭ по математикеСкачать

Исследовательская работа «Круг в нашей жизни»
Разделы: Математика
Круг и окружность – одни из самых древнейших геометрических фигур, философы древности придавали им большое значение. Круг – воплощение нескончаемого Времени и Пространства, символ всего сущего, Вселенной. “Из всех фигур прекраснейшая – круг”, – считал Пифагор.
Вокруг нас много круглых предметов. Представьте себе на секунду, что вдруг случилась беда: на Земле исчезло все круглое! Казалось бы – пусть все будет квадратным. Разве нельзя прожить без круглых труб, а к квадратным колесам нельзя привыкнуть? Можно ли вообще представить жизнь человека без использования круга? Почему так много тел имеют круглую форму? Чтобы найти ответы на все эти вопросы, в первую очередь, необходимо рассмотреть историю возникновения этих понятий и дальнейшее их развитие.
История возникновения и развития геометрических понятий “круг” и “окружность”.
Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова, вкусные орехи от горьких и т.д. Особенно вкусными казались им орехи кокосовой пальмы, похожие на шар. Специальных названий для геометрических фигур, конечно, не было. Говорили: “такой же, как кокосовый орех” или “такой же, как соль” и т.д. Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими фигурами.
Круглые тела еще в древности заинтересовали человека. В Древнем Египте для постройки знаменитых египетских пирамид никаких технических сооружений еще не было. Даже шлифовать огромные каменные глыбы приходилось вручную, а перемещали их с помощью бревен круглой формы. Заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел – цилиндром. Скалками цилиндрической формы пользовались и женщины, раскатывая белье после стирки. Перевозить грузы на катках было довольно тяжело, потому что сами древесные стволы весили много. Чтобы облегчить работу, стали вырезать из стволов тонкие круглые пластинки, которые катились уже легче и с их помощью перетаскивали грузы. Так появилось первое колесо. К сожалению, неизвестен непосредственный изобретатель колеса.
Не только в процессе работы люди знакомились с различными фигурами. Издавна они любили украшать себя, свою одежду, свое жилище. И многие, созданные давным-давно украшения, имели ту или иную форму. Бусинки были шарообразными, браслеты и кольца имели форму окружности. Древние мастера научились придавать красивую форму бронзе, золоту, серебру, драгоценным камням. Художники, расписывавшие дворцы, тоже использовали окружность. Со времени изобретения гончарного круга люди научились делать круглую посуду – горшки, вазы, амфоры. Круглыми были и колонны, подпирающие здания.
Математические знания египтян и вавилонян были разрозненные и представляли собой свод правил, проверенных практикой. В Древней Греции все разрозненные знания привели в систему, геометрия стала бурно развиваться как наука. Только в Древней Греции “окружность” и “круг” получили свои названия, почти все названия геометрических фигур греческого происхождения, как и само слово геометрия (“гео” – земля, а “метрио” – мерить). Однако эти слова вошли в русский язык не непосредственно с греческого, а через латинский язык.
В Древней Греции многие свойства фигур, в том числе круга и окружности были сформулированы в виде теорем и доказаны. Наиболее удачно была изложена геометрия, как наука о свойствах геометрических фигур, греческим ученым Евклидом (III в. до н. э.) в своих книгах “Начала”. В течение многих веков “Начала” были единственной учебной книгой, по которой молодежь изучала геометрию. И даже сейчас, в наше время, учебники написаны под большим влиянием “Начал” Евклида.
Окружность и круг – это плоские фигуры . Мы живем в мире трех измерений. А в какое геометрическое тело превратятся окружность и круг, если попадут в пространство? Это сфера и шар. “Сфера” – произошло от греческого слова “сфайра”, в переводе – “мяч”. Кроме этого геометрия пространства рассматривает и другие круглые тела – это “цилиндр” (от греческого слова “кюлиндрос”, что означает “валик”, “каток”) и “конус” (от греческого слова “конос”, означающего “сосновая шишка”). Самым важным среди круглых тел был шар.
Итак, в Древней Греции круг и окружность считали венцом совершенства. “В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе”. Это свойство окружности стало толчком к возникновению колеса (Приложение 5). (Приложение 2).
Круг – “циркулус” – латинское слово, от него же и “циркуль”, без которого бы мы не построили круг. Циркуль и линейка – самые старые чертежные инструменты на Земле. (Приложение 3.)
Элементы окружности и круга (Приложение 2):
Радиус окружности – это отрезок, соединяющий центр окружности с любой ее точкой (по-латыни – спица колеса).
Диаметр окружности – это хорда, проходящая через центр окружности (с греческого – “поперечник”).
Хорда окружности – отрезок, соединяющий любые две точки на окружности (с греческого– “струна”).
Дуга окружности – это часть окружности, ограниченная двумя точками.
Часто в практических задачах нужно узнать длину окружности. А как измерить длину окружности, если сама окружность – кривая линия, а единица измерения длины – отрезок? Есть несколько способов измерения длины окружности (Приложение 1).
Однако эти способы непосредственного измерения длины окружности малоудобны и дают приближенные результаты. Поэтому уже с древних времен начали искать более совершенные способы измерения длины окружности. В процессе измерений заметили, что между длиной окружности и длиной ее диаметра имеется определенная зависимость: С:d ≈ 3,1.
Многие ученые – математики пытались доказать, что это отношение есть число постоянное, не зависящее от размеров окружности, его стали обозначать греческой буквой π-ο ервая буква греческого слова “периферия” – круг.
С:d = π, где С – длина окружности, d – длина диаметра, отсюда и формула длины окружности C = πd или C = 2πr.
Изучив исследования ученых математиков, мы провели следующие измерения и вычисления:
1. Вычисление числа пи : а) с помощью тонкой нити измерили длину окружности С некоторых предметов быта; б) чтобы точнее найти длину диметра d, приложили этот предмет к листу бумаги и обвели карандашом, вырезали, свернули пополам, линия сгиба – это диаметр, измерили его с помощью линейки; в) нашли отношение С:d, данные занесли в таблицу:
| Предметы | Длина окружности С | Диаметр d | Отношение С:d |
| Стакан | 22 см | 7 см | 3.1428 |
| Ведро | 82 см | 26 см | 3.1538 |
| Тарелка | 62 см | 19,5 см | 3,1794 |
| Кастрюля | 69 см | 22 см | 3.1363 |
| Бидон | 52 см | 16,5 см | 3,1515 |
2. Границы значения числа пи: а) с помощью циркуля вписали круг в квадрат: если диаметр равен 1,то длина окружности равна π . Периметр квадрата со стороной 1 равен 4. Значит π меньше 4. (Приложение 6. Рис.1). б) в этот же круг вписали правильный шестиугольник: диаметр круга снова 1, длина окружности равна π . Сторона правильного шестиугольника равна радиусу, т.е.0,5,а периметр равен 6·0,5=3,значит π больше 3 (Приложение 6. Рис.2).
В результате мы убедились, что отношение длины окружности к ее диаметру (число π) есть число постоянное и 3 ‹ π ‹ 4 ,т.е. мы подтвердили исследования ученых – математиков.
Одна из загадок числа π состоит в том, что оно не может быть выражено какой – либо точной дробью. История числа π достойна восхищения, многие математики затратили на его вычисления не один десяток лет. Уточнялись нижняя и верхняя оценки числа и предпринимались неудачные попытки представить π в виде дроби и, таким образом, окончательно найти его значение (Приложение 4). Пока рекорд принадлежит японскому математику, в 2004 году – Ясума Канада из Токио рассчитал число π на компьютере до 1,24 триллиона знаков.
π -3,141 592 653 589 793 238 462 643 383279 502 884197 169 399 375 105 ….
Зачем нужно π, да еще с такой точностью? Число π чрезвычайно важно для ученых и инженеров. Все, что круглое и все, что движется по кругу (как колеса или планеты), содержит π. Без π люди не могли создать автомобили, понять движение планет или сосчитать сколько гороха поместится в консервную банку. Но загадка таинственного числа не разрешена вплоть до сегодняшнего дня, и, по-прежнему, волнует ученых. В настоящее время с числом π связано труднообозримое множество формул, математических и физических фактов. Их количество продолжает стремительно расти. Все это говорит о возрастающем интересе к важнейшей математической константе, изучение которой насчитывает уже более двадцати двух веков.
Изучив литературу и проделав собственные измерительные исследования с окружностью и кругом, мы пришли к следующим выводам: окружность и круг – это удивительно гармоничные фигуры. Окружность – единственная кривая, которая может “скользить сама по себе”, вращаясь вокруг центра. Это свойство окружности дает ответ на вопросы, почему для ее вычерчивания используют циркуль, и почему колеса делают круглыми, а не квадратными или треугольными.
Круг в окружающей жизни.
Исследуя вопрос о роли круга в окружающей жизни, мы провели анкетирование обучающихся 5-9 классов и педагогов МО ШИСП (всего 90 человек):
- Какие круглые тела вы встречаете в окружающей жизни?
- Какое значение имеет круг в других науках?
- Какие практические задачи повседневной жизни решаются, используя знания о круге и окружности?
- Как вы считаете, почему встречается так много круглых тел в природе?
Ответы на первый вопрос представлены в презентации.
Из ответов учителей – предметников на второй вопрос анкеты мы поняли, что круг имеет большое значение не только в математике, но и в других науках:
| Предмет | Использование |
| Физика и астрономия | Движение небесных тел происходит по круговым орбитам. Зодиакальный круг, астрономический круг. Круг с точкой в центре символизирует солнце. |
| География | Меридианы и параллели, определяющие положение тела на земном шаре, экватор. Круговые процессы-циклы: круговорот воды и веществ в природе. Смена времен года, смена дня и ночи. |
| Химия | Строение атома: ядро круглое, электроны вращаются вокруг ядра по круговым орбитам. |
| Биология | У всех клеток есть круглое ядро. Круглую форму имеют клетки крови, цилиндрическую – клетки многих желез. Стебли растений и стволы деревьев, кости человека – круглые. Кровообращение идет по кругу. Овощи и фрукты имеют шарообразную или конусовидную форму. Цикличность развития живых существ. |
| Русский язык | В русском языке слово “круглый” означает высокую степень чего-либо: “круглый отличник”, “круглый сирота” и даже “круглый дурак”. От слова круг образовано множество различных слов: круглый, кругленький, округлить, округлиться, округлый, кругом, вокруг, окружать, кружить и многое другое. Округлые формы, круглое лицо, кругленькие щеки, круглый год, голова идет кругом, ходить по кругу – часто употребляемые выражения. |
| История и обществознание | “Круглый стол” – конференции, кругооборот капитала, круг семьи , колесо истории, “большой и малый круг истории” – исторические циклы. |
Проанализировав ответы на третий вопрос анкеты, мы поняли, что знания о круге и окружности позволяют человеку решать многие практические задачи в повседневной жизни: разбить клумбу или фонтан, сделать круглую крышу, окно или крышку, сшить головной убор, связать салфетку, сделать елочную игрушку, сделать выкройку платья или юбки, нарисовать узор и т.п.
Таким образом, круг в жизни человека имеет очень важную роль, и в жизни без круглых предметов обойтись невозможно.
Не все, кого мы анкетировали, смогли дать ответ на четвертый вопрос.
Здесь мы помещаем самые интересные и распространенные ответы:
- Только круглые предметы могут катиться, и поэтому их легче перемещать.
- Потому что, куда бы мы не пошли, мы возвращаемся, т.е. идем по кругу.
- У круга нет углов, и поэтому он удобен в применении, например, круглые монеты не могут порвать карман, о них не уколешься, не порежешься.
- Мячик не может быть квадратным, он не будет отпрыгивать.
- Посуду делали из глины, и округлую форму было легче придать, чем квадратную. Круглую посуду легче мыть, не надо выскребать из углов, в ней удобней размешивать.
- Легче изготовить круглое, чем угловатое. Многие технические процессы легче для тел вращения.
- На круглую форму идет меньше материала, чем на квадратную.
- Круглая крышка люка никогда не провалится, в отличие от квадратной.
- Все банки и крышки круглой формы, т.к. каждая точка окружности является точкой концентрации напряжения, и ее легко открыть, у прямоугольной формы такими точками являются только углы.
- Потому ,что солнце круглое, а без солнца мы не могли бы существовать.
- Круглая форма универсальна в природе.
Почему же на самом деле встречается так много круглых тел? Мы обратились к научным источникам. На этот вопрос можно ответить, рассмотрев мыльный пузырь, т.к. он идеально круглой формы. Силы поверхностного натяжения не дают лопнуть мыльному пузырю и стремятся придать мыльному пузырю максимально компактную форму. Самая компактная форма в природе – это шар. При шарообразной форме воздух внутри пузыря равномерно давит на все участки его внутренней стенки.
В небе много круглых объектов: Солнце, Луна, планеты, звезды. Почему не быть хотя бы одной некруглой планете? Ну, пусть одна, будет кубическая или пирамидальная. Но это невозможно? Есть сила, которая во всей Вселенной превращает миры в гладкие шары. Эта сила – сила тяготения. Каждый предмет имеет свою гравитацию, притягивает к себе другие тела, а также и свои части. Чем больше тело, тем сила тяжести увеличивается. Земля наша огромная, поэтому она имеет свою большую силу тяжести, которая заставляет притягиваться все к ее центру, а тело преобразовываться в шар. Если бы в силу каких-то причин удалось изменить нашу планету и придать ей иную форму, не шара, то спустя некоторое время она снова стала бы шарообразной. С телами на земле это не происходит, потому что их сила очень маленькая и сила тяжести Земли препятствует этому. Но если взять, например, каплю воды и запустить в космос, она сразу же преобразуется в шар. Именно жидкость способна преобразовываться в шарообразную форму. Земля состоит в основном из магмы (жидкости) поэтому и имеет форму шара.
Таким образом, мы пришли к выводам, что сама природа выбирает эту удобную и компактную форму – шара.
Кроме того, окружность и круг в виде сферы и шара – самая распространенная форма во Вселенной.
Круг и окружность – это еще и траектория движения Земли вокруг Солнца, это перемещение звезд на небе, это цикличность всех процессов, происходящих в мире. Если бы необходимо было бы выбрать форму, наиболее точно передающую устройство мира, то это были бы окружность и круг.
Изучив научную литературу, мы сделали вывод, что с незапамятных времен люди используют в своей жизни круг.
1. Около 3300 года до нашей эры стали применять гончарный круг, делать круглую посуду – тарелки, вазы, кастрюли, горшки, сковородки. У посуды есть окружность (верхний край) и круг (дно).
2. Мы не можем представить свою жизнь без машин: автобус, трактор, велосипед, швейная, стиральная и пишущая машинки, самолет, вездеход, луноход, различные станки, подъемный кран…Они не похожи друг на друга, но присмотримся к ним повнимательнее. Есть у них у всех похожие части – детали, и одна из них – колесо. Сначала колеса были круглые и гладкие, чтобы по земле легко катились, а потом человек придумал много разных колес. Зубчатые колеса спрятаны внутри многих машин, одно колесо заставляет вращаться другое, колеса с желобком –блоки, помогающие поднимать тяжелые грузы. Машины из века в век совершенствовались и совершенствуются, но неизменным остается использование в них колеса, как основной детали.
3. Круг и окружность широко применяются в архитектуре и искусстве: круглые арки, своды, купола. Круг – это форма кочевых шатров и поселений, у многих народов символизирующая динамизм и бесконечное движение в противовес квадратам домов, участкам земли и городам оседлых и зерносеющих народов. Еще древние греки обнаружили, что с помощью циркуля и линейки можно построить множество фигур, включая шестиугольники, квадраты и другие правильные многоугольники, и создавать волшебные узоры.
4. Необозрима сфера применения круга в математике: тригонометрический круг, круги Эйлера, задачи на построение, круговые диаграммы и т.д. Многие приборы имеют круглую шкалу, в математике таким прибором является транспортир (Приложение 7).
Есть в математике задачи, которые до сих пор не разрешены, например, знаменитая задача о “квадратуре круга” – о построении квадрата, равновеликого данному кругу и т.д.
5. Картинки с волшебными кругами люди используют в медицинских целях, когда на них смотришь, кажется, что они двигаются. Если смотреть на них несколько минут, то проходит головная боль (Приложение 8).
6. Также человек использует круг, как универсальный символ, означающий целостность, непрерывность, первоначальное совершенство, бесконечность, отсутствие начала и конца, верха и низа, цикличность, повторяемость, завершенность. Три концентрических круга символизируют прошлое, настоящее и будущее; три сферы земли: землю, воздух и воду; небесные миры, землю и преисподнюю; фазы луны; восходящее, полуденное и заходящее солнце. Многие народы используют круг в религии, как символ связи земного с космосом.
В последнее время в разных местах земного шара стали появляться круги на полях, которые создают посланцы иных миров, желая о чем-то предупредить землян. (Приложение 9).
7. В энциклопедии мы нашли еще много понятий связанных с кругом: кругловязальная машина, круглочулочный автомат, круглогубцы, кругломер, “круговая система” в спорте, кругозор, круг друзей, круг общения, спасательный круг, святой круг, спиритический круг, круговая оборона, круговая порука, круглосуточная аптека, круги вокруг глаз.
- Круг в жизни человека имеет очень важную роль, и без использования круглых предметов обойтись невозможно.
- Окружность и круг – удивительно гармоничные, совершенные, простые фигуры. Окружность – единственная замкнутая кривая, которая может “скользить сама по себе”, вращаясь вокруг центра, поэтому колеса делают круглыми, а не квадратными или треугольными.
- Круг – это колесо. Колесо – это прогресс – движение вперед. Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы.
- Круг – символ цикличности, повторяемости. Все движется по кругу.
- Круг дает ощущение взаимосвязи с Космосом.
- Сама природа выбирает эту удобную и компактную форму как шар и круг.
Видео:7 класс, 23 урок, Примеры задач на построениеСкачать

Двадцать задачек (по безумной, восхитительной геометрии)
Предупреждение врача. Остерегайтесь этих головоломок. Побочные эффекты могут включать потерянное послеобеденное время, скомканные волосы и восклицания «А-а-а-х, вот как это делается» настолько громкие, что могут треснуть оконные стёкла.
Несколько месяцев назад я наткнулся в твиттере на математические головоломки Катрионы Ширер. Они сразу меня увлекли: каждая головоломка такая осязаемая, ручной работы, словно просит её решить. И на каждую вы можете легко потратить час времени, а то и больше.
Катриона разрешила мне подвесить вас на эти задачки — и поделилась 20 своими любимыми головоломками. Она даже удовлетворила моё любопытство и восхищение, дав интервью (см. в конце статьи).
Наслаждайтесь. И не говорите, что врач не предупреждал.
Видео:Профильный ЕГЭ 2024. Задача 1. ОкружностьСкачать

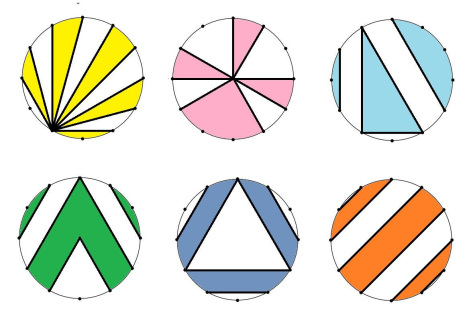
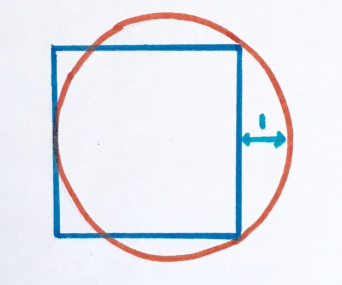
1. Сад часов
Какая часть каждого круга закрашена? (12 точек на равном расстоянии; единственная точка внутри круга — его центр)
«К сожалению, из эти шести моя любимая — единственная, которую я не придумала сама, — говорит Катриона, — это тёмно-синяя».
Видео:Как решать задания на окружность ОГЭ 2021? / Разбор всех видов окружностей на ОГЭ по математикеСкачать

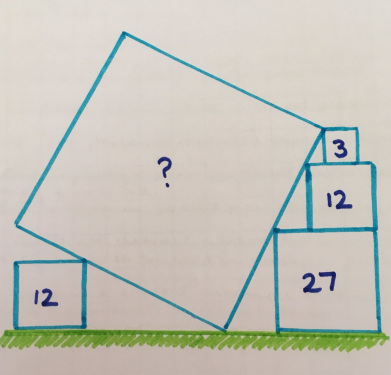
2. Опрокинутый квадрат
(Как по мне, это классика).
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

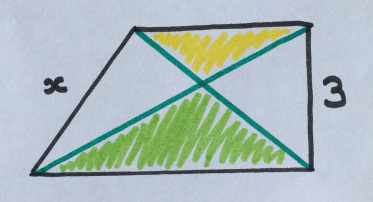
3. Это ловушка
В прямоугольной трапеции зелёная область на 6 больше, чем жёлтая. Чему равен x?
«Это „вторая версия” данной головоломки: она лучше, чем первая, которую я придумала».
Видео:Окружность и задачи на построениеСкачать

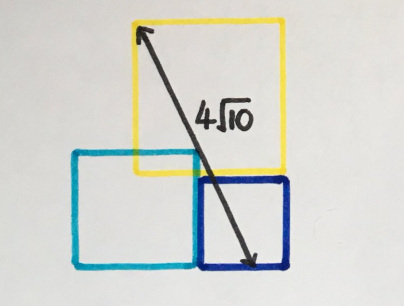
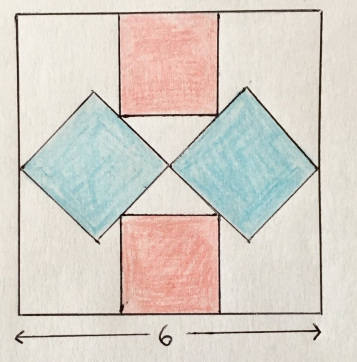
4. Три квадратных тарелки
Длины сторон трёх квадратов — последовательные целые числа. Какова общая площадь?
«Эта мне очень нравится: на её основе я нарисовала много красивых узоров».
Видео:7 класс, 21 урок, ОкружностьСкачать

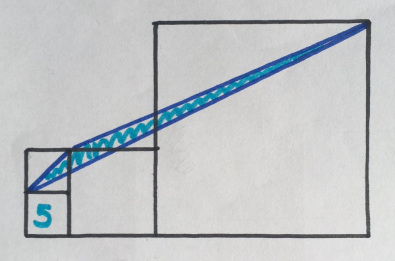
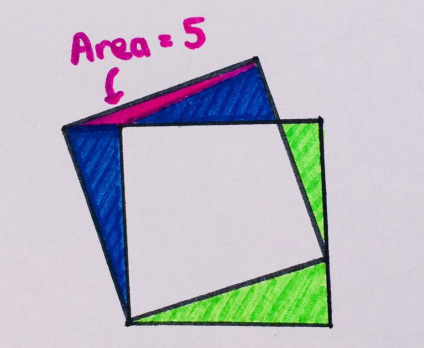
5. Красивая стрижка
Площадь левого нижнего квадрата 5. Какова площадь синего треугольника?
«Наверное, моя любимая за всё время. Выглядит просто невозможным! Здесь метод решения называется «стрижка», shearing (к сожалению, не в мою честь)».
Видео:✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

6. Все люди рождены равными
«Ещё одна переделка, которую я предпочитаю оригиналу».
Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

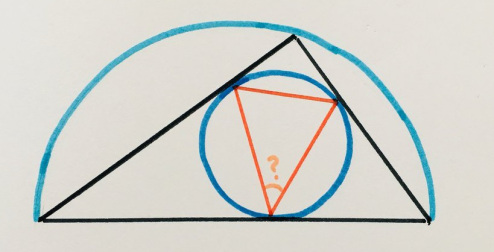
7. Полукруг турдакен
«Головоломки с углами гораздо труднее составлять. Ученики сказали, что это довольно простая задачка, но мои родители испытали большие трудности. Кажется, эта головоломка требует больше „знаний”, но сам процесс решения проще».
Видео:ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

8. Степенные хорды
Какова площадь круга?
«В школе я не изучала теорему о пересекающихся хордах, поэтому люблю везде её использовать!»
Видео:Движение по окружности | задачи ЕГЭ по профильной математикеСкачать

9. Сказка о двух кругах
У этих правильных многоугольников одинаковый периметр. Найдите отношение площадей вписанных окружностей.
«Это следствие другой головоломки, но она мне нравится больше, чем оригинал!»
Видео:Задачи на движение по окружности. ЕГЭ по математике 2020Скачать

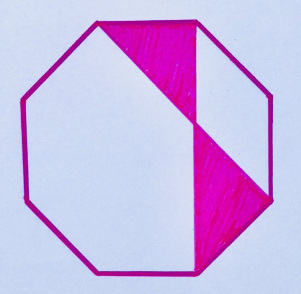
10. Doc Oct
У закрашенной области такое же значение, как у периметра правильного восьмиугольника. Каково значение?
«Думаю, это довольно чистая задачка, хотя выглядит как массовое разграбление головоломок Эда Сауталла».
Видео:Задача про Земной шар и мышьСкачать

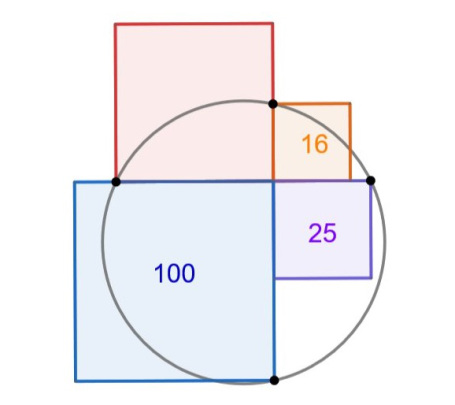
11. Всё в квадрате
«Мне нравится то, что хотя вы здесь можете найти все стороны оранжевого треугольника (и я это сделала, когда решала), но на самом деле это не нужно — достаточно площади и гипотенузы».
Видео:Математика 5 класс (Урок№26 - Окружность и круг. Сфера и шар.)Скачать

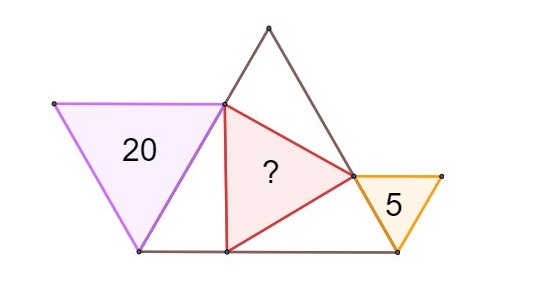
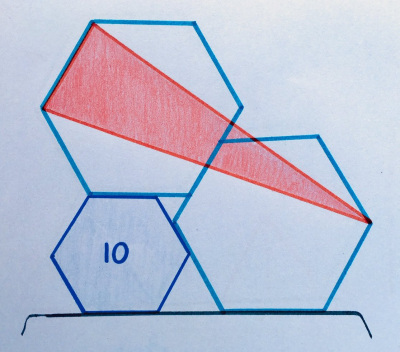
12. Шип в улье
Два из правильных шестиугольников идентичны; у третьего площадь 10. Какова площадь красного треугольника?
«Довольно неплохо: мне нравится, что не нужно иметь дело с любой длиной стороны, которые почти наверняка ужасны».
Видео:Длина окружности. Практическая часть - решение задачи. 6 класс.Скачать

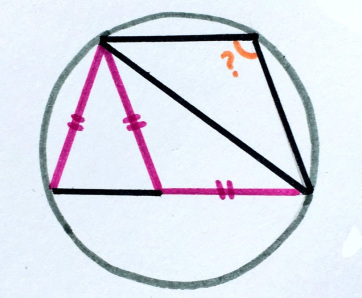
13. Я видел равнобедренных
Все четыре треугольника равнобедренные. Найдите угол.
«Думаю, что формулировка этой задачки идеальна. Многие пропускают важную информацию и приходят к выводу, что есть бесконечное число решений!»
Видео:Самая сложная задача из самой сложной олимпиады [3Blue1Brown]Скачать
![Самая сложная задача из самой сложной олимпиады [3Blue1Brown]](https://i.ytimg.com/vi/S6_R5j8hzbY/0.jpg)
14. Зеленый против синего
На картинке больше зелёного цвета или синего (и на сколько)?
«Ещё одна из моих любимых».
Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

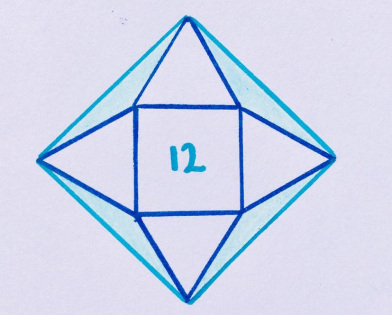
15. Резцы по камню
Четыре равносторонних треугольника расположены вокруг квадрата с площадью 12. Какова закрашенная площадь?
«Тут самое лучшее — действительно хорошие решения по рассечению площади».
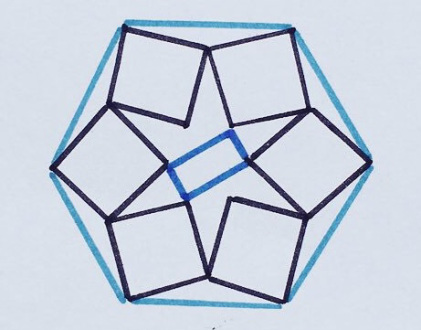
16. Едем, едем, уехалиугольник
Шесть одинаковых квадратов и меньший прямоугольник вписаны в этот правильный шестиугольник. Какую часть шестиугольника они занимают?
«Здесь ответ не такой красивый, но очень удивил меня. Думаю, из-за своей сложности эта задачка не получила такого распространения в твиттере, как другие!»
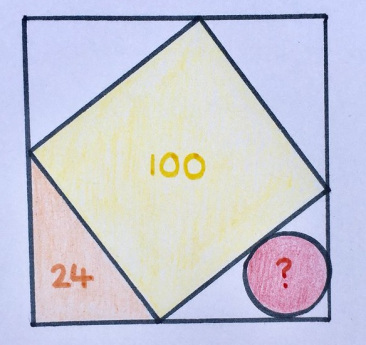
17. Только один факт
Какова площадь этого квадрата?
«Это одна из моих любимых, потому что сначала кажется, что информации недостаточно».
18. Стиральная машина
Какая часть большого квадрата закрашена?
«Здесь мне нравится сумбур квадратов, как они грохочут вокруг словно в стиралке. И ответ тоже удивительно красивый».
19. Летающие флаги
У квадратов одного цвета одинаковый размер. Какова площадь всех закрашенных областей?
«Это довольно просто, как только вы поймёте — но я поняла не сразу, поэтому простота ответа меня удивила».
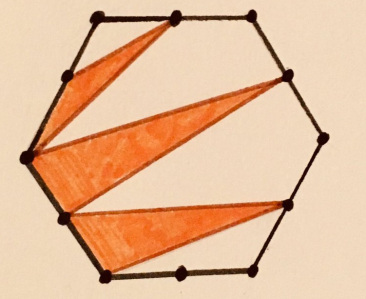
20. Тигрогон
Какая часть фигуры закрашена? Шестиугольник правильный, с равномерно расположенными точками по периметру.
«Эту я редко публиковала. Но картинка напоминает мне Тигра Тони [с пачек быстрого завтрака Kellogg — прим. пер.]».
БОНУС:
Закат над Квадратным городом
У левого квадрата площадь 4. Какова площадь правого квадрата?
«Мне нравится эта задачка, она напоминает закат над городом скверов.”
Если вы дочитали до этого места — возможно, через 6 месяцев после начала чтения — и ваш стол окружен скомканными бумагами и пустыми китайскими контейнерами для продуктов питания, то вам будет приятно почитать небольшое интервью с Катрионой.
Как вы пришли к разработке своих головоломок?
Я поехала в отпуск в Шотландское высокогорье, но забыла взять пальто, поэтому пришлось сидеть в домике в одиночестве, пока друзья гуляли на природе! Ничего не оставалось, кроме как машинально чертить линии на бумажке.
Не ожидала, что это превратится в хобби, но это немного затягивает, особенно когда люди присылают в ответ свои решения, которые мне нравятся. Почти всегда можно красиво сократить головоломку, что я пропустила.
Как проходит творческий процесс?
Всё начинается с рисования бессмысленных фигурок. В итоге получается целая страница перекрывающихся квадратов под разными углами или правильных (типа) пятиугольников с разными закрашенными частями, а потом я смотрю, есть ли там какая- то хорошая математика — отношения между длинами или площадями или углами.
Многие из ваших задачек нарисованы маркером на бумаге. Почему такой лоутек?
Я пробовала использовать Desmos и Geogebra, но не очень понравилось. По-моему, быстрее нарисовать вписанный круг вручную, после небольшого количества проб и ошибок, чем красиво строить его в геометрии программного обеспечения.
Кроме того, при использовании фломастера вы можете выдумывать вещи, потому что линии настолько толстые. Это хороший компромисс между тем, чтобы выглядеть «правильно», но также знать, что вы не можете просто вытащить линейку и измерить фигуру.
Одна из приятных вещей в геометрии — что она многое прощает. Я могу показать вам безнадёжный квадрат или круг, но этого достаточно, чтобы передать концепцию, потому что они так хорошо определены.
Некоторые из ваших головоломок дают самый минимум информации. Как вы находите эту границу, где диаграмма как раз определена?
Иногда этот минимум на самом деле подсказка, потому что он отправляет вас по одной дороге. Я предпочитаю давать чуть больше необходимого, поэтому есть несколько обманных маршрутов. Это также даёт большее разнообразие решений!
Было дело, я опубликовала пару невозможных головоломок: к счастью, кто-нибудь обычно указывает на это довольно быстро!
Я также публиковала задачки с массивным количеством излишней информации, потому что не видела хорошего решения, чтобы использовать только половину информации.
Советы для потенциальных создателей головоломок?
Отлично, тут мой синдром самозванца полностью проявится. Я определённо ещё новичок — я занимаюсь этим только с августа [статья опубликована в октябре 2018 года — прим. пер.]! С другой стороны, мне нравится создавать головоломки и читать решения даже больше, чем решать их самой.
Основной целью головоломки должно быть развлечение — вот что отличает её от стандартной математической задачи. Таким образом, вам нужно по крайней мере два из трёх:
- Красивая постановка задачи. Предоставьте минимум информации, чтобы читателю стало интересно, как вообще можно решить такую задачу. Или несколько дразнящих кусочков информации, каждый из которых якобы предлагает способ решения. Правильные многоугольники и круги — фантастические штуки, потому что скрывают огромное количество информации.
- Красивый метод. Трюк или кратчайший путь, или внезапное озарение, которое всё упрощает. Это может быть не самый очевидный метод. Я видела много задачек, которые решаются с помощью алгебры или иррациональных чисел, или ужасных выражений с pi, а в конце всё внезапно сокращается — и я понимаю, что есть более простой способ.
- Красивый ответ. Мало удовольствия работать над головоломкой, чтобы в конце получить некрасивый ответ.
В принципе, начните рисовать — найдите головоломку, которую вам понравилось решать, и подумайте, как можно её расширить или изменить некоторые элементы. Если вдруг попадутся соотношения, которые вас удивляют, то с высокой вероятностью они удивят и других. Twitter — отличная платформа, так как люди могут публиковать в ответ собственные картинки.