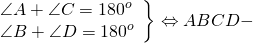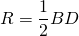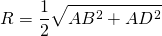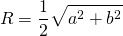- Четырехугольники, вписанные в окружность. Теорема Птолемея
- Вписанные четырёхугольники и их свойства
- Теорема Птолемея
- Четырехугольник, вписанный в окружность
- Многоугольник. Свойства четырехугольников вписанных в окружность.
- Тема: «Применение производной к решению экстремальных задач»
- Главная > Документ
- Прямоугольный участок земли, примыкающий к стене заводского здания, нужно оградить забором. Часть забора, параллельная стене, должна быть каменной, а остальная часть деревянной. Площадь участка 90см. Стоимость 1м каменного забора 10руб, а деревянного 8руб. Найдите такие размеры участка, чтобы стоимость всей ограды была наименьшей?
- Задача №6. Найти наибольший объем цилиндра, вписанного в данный конус
- Задача №8. В трапецию ABCD , боковая сторона АВ , которой
- (длина 8 см ) перпендикулярна основанию, вписать прямоугольник наибольшей площади так, чтобы одна из его сторон лежала на большем основании трапеции. Основания трапеции равны 6 и 10 см cоответственно. Вычислить площадь этого прямоугольника.
- Задача № 10. В круг радиуса а вписан равнобедренный треугольник. При каком соотношении сторон треугольник будет иметь наибольшую площадь.
- Четырехугольник, вписанный в окружность — основные свойства, признаки и формулы
- Общие сведения
- Основные правила
- Свойства и утверждения
- Формулы и соотношения
- Периметр и полупериметр
- Понятие площади
- Диагонали и углы
- Параметры для окружности
- 🎬 Видео
Видео:Прямоугольник и окружностьСкачать
Четырехугольники, вписанные в окружность. Теорема Птолемея
 Вписанные четырехугольники и их свойства Вписанные четырехугольники и их свойства |
 Теорема Птолемея Теорема Птолемея |
Видео:Вписанный в окружность прямоугольный треугольник.Скачать

Вписанные четырёхугольники и их свойства
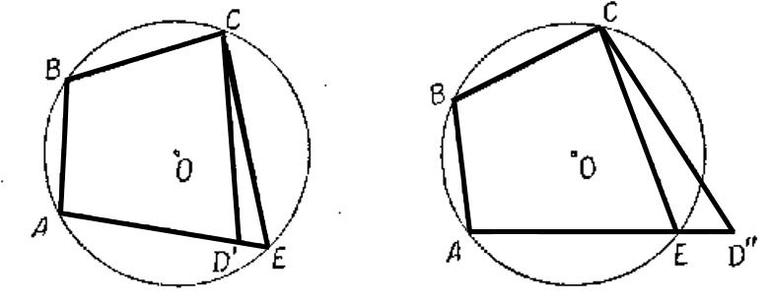
Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .
Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .
Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .
Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.
Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.
Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).
Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.
Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.
Теорема 2 доказана.
Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.
| Фигура | Рисунок | Свойство | |||||||||||||||||||||||||||||||||||
| Окружность, описанная около параллелограмма |  | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | |||||||||||||||||||||||||||||||||||
| Окружность, описанная около ромба |  | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | |||||||||||||||||||||||||||||||||||
| Окружность, описанная около трапеции |  | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | |||||||||||||||||||||||||||||||||||
| Окружность, описанная около дельтоида |  | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | |||||||||||||||||||||||||||||||||||
| Произвольный вписанный четырёхугольник |  | ||||||||||||||||||||||||||||||||||||
| Окружность, описанная около параллелограмма | |||||||
 | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | ||||||
| Окружность, описанная около ромба | |||||||
 | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | ||||||
| Окружность, описанная около трапеции | |||||||
 | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | ||||||
| Окружность, описанная около дельтоида | |||||||
 | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | ||||||
| Произвольный вписанный четырёхугольник | |||||||
 | |||||||
| Окружность, описанная около параллелограмма |
 |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

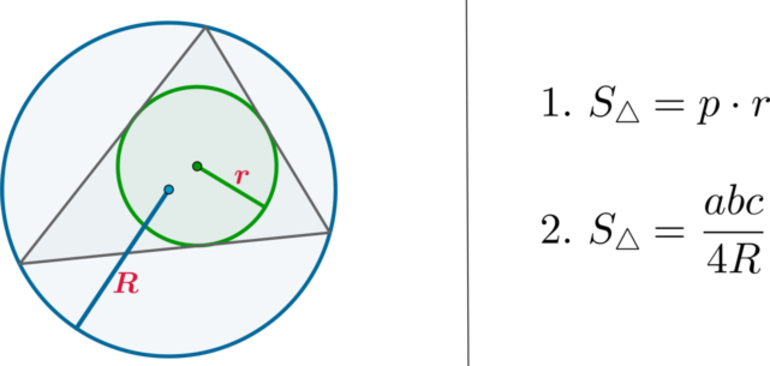
Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:
где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Теорема Птолемея
Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).
Докажем, что справедливо равенство:
Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).
Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
откуда вытекает равенство:
 | (1) |
Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
Видео:Задача.Окружность и прямоугольник вписаны в квадрат.Скачать

Четырехугольник, вписанный в окружность
Рассмотрим, что такое четырехугольник, вписанный в окружность и около какого четырехугольника можно описать окружность.
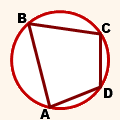
Четырехугольник называется вписанным в окружность, если все вершины четырехугольника лежат на окружности.
Четырехугольник ABCD — вписанный в окружность.
Все его вершины — точки A, B, C, D — лежат на окружности.
1) Четырехугольник можно вписать в окружность, если сумма его противолежащих углов равна 180º.
2) Если сумма противолежащих углов четырехугольника равна 180º, то этот четырехугольник можно вписать в окружность.
вписанный в окружность.
1) Из всех параллелограммов вписать в окружность можно только прямоугольник (в том числе, в квадрат).

Радиус описанной около прямоугольника окружности равен половине его диагонали.
Через стороны прямоугольника радиус описанной окружности равен
Если стороны прямоугольника обозначить как a и b, то
2) Из всех трапеций вписать в окружность можно только равнобедренную трапецию.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Многоугольник. Свойства четырехугольников вписанных в окружность.
Если все вершины какого-нибудь многоугольника (ABCDE) лежат на окружности, то говорят, что этот многоугольник вписан в окружность, или что окружность описана около него.
Теорема.
В выпуклом вписанном четырехугольнике сумма противоположных углов равна двум прямым углам (2d).
Обратная теорема:
Если в выпуклом четырехугольнике сумма противоположных углов равна двум прямым углам (2d), то около него можно описать окружность.
Пусть ABCD — вписанный выпуклый четырехугольник. Необходимо обосновать, что:
Углы B и D, как вписанные будут равны: первый — половиной дуги ADС, второй — половиной дуги ABС. Следовательно, B + D равняется полусумме дуг ADС и ABС, т.е. половиной окружности. Значит, B + D = 2d. Подобно этому убедимся, что A + С= 2d .
Необходимо обосновать, что около такого четырехугольника можно описать окружность. Через какие-нибудь три его вершины, например, A, B, С прочертим окружность (что всегда можно сделать).
Четвертая вершина D должна располагаться на этой окружности, потому что в противном случае угол D лежал бы своей вершиной или внутри круга, или вне его, и тогда этот угол не измерялся бы половиной дуги ABС, поэтому сумма B + D не измерялась бы полусуммой дуг ADС и ABС, т.е. сумма B + D не равнялась бы 2d, что противоречит условию.
Следствия.
1. Из всех параллелограммов только около прямоугольника можно описать окружность.
2. Около трапеции можно описать окружность только тогда, когда она равнобедренная.
Видео:ОКРУЖНОСТЬ и ПРЯМОУГОЛЬНИК. ГЕНИАЛЬНО!Скачать

Тема: «Применение производной к решению экстремальных задач»
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Теорема 2 (второе правило).
Если для дифференцируемой функции f(x) в некоторой точке х 0 ее первая производная f'(x) равна нулю, а вторая производная f»(x) существует и отлично от нуля, т. е. f'(x 0 )= 0, f»(x 0 )≠0, то в этой точке функция f(x) имеет экстремум;
если f»(x 0 )>0, то f(x 0 )- минимум функции f(x), и
если f»(x 0 ) 0 )- максимум функции f(x).
Положим, что f'(x 0 )=0, f»(x 0 ), пусть x=x 0 +
Т.к. вторая производная f»(x) есть производная от первой производной f'(x), то имеем:
Таким образом, переменная
стремится к пределу f // (x 0 )≠0, а значит, начиная с некоторого момента, это величина имеет знак своего предела в нашем случае плюс. поэтому:

Мы видим, что производная f / (x) при переходе через точку х 0 меняет свой знак с минуса на плюс, т.е. минимум функции.
Аналогично доказываем, что если f / (x 0 )=0 и f // (x 0 ) f ( x 0 )- минимум функции f (х).
Дан треугольник АBC, основание которого AC=b и высота BL=h. Найти прямоугольник наибольшей площади, который можно вписать в этот треугольник.

Обозначим высоту KL прямоугольника через х , основание DE через у . Тогда площадь его S=xy . Переменные х и y не являются независимыми, они связаны некоторыми соотношением.
В самом деле из подобия треугольников DBE и ABC , учитывая, что высоты их BK и BL пропорциональны основаниям DE и AC имеем
или т.к . BK=h-x, DE = y, BL=h, AC=b,
то 
исключая у из выражения для S находим
S =
Ищем максимум для этой функции
S 

S 

Легко видеть, что значение х действительно даст максимум функции S. В самом деле, составляя вторую производную, будем иметь
следовательно, при 

Ответ: площадь наибольшего прямоугольника, вписанного в треугольник, равна половине площади этого треугольника.
§6. Нахождение промежутков монотонности и экстремумов функции.
Решение таких примеров рекомендуется проводить по следующей схеме:
Найти область определения заданной функции 
Найти производную 
Определить критические точки функции 
Найти промежутки знакопостоянства производной и указать промежутки возрастания и убывания функции f(x)
Указать, в каких точках функция имеет максимумы и минимумы, вычислить её экстремальные значения.
Найдем промежутки возрастания и убывания, а также точки максимума и минимума функции
3)Найдем критические точки:
4


Ответ: функция возрастает на
Функция убывает на
§7.Нахождение наименьшего и наибольшего значений функции на заданном отрезке.
Определение наименьшего и наибольшего значений дифференцируемой функции на заданном отрезке [а; b ] рекомендуется проводить по следующей схеме:
1)Найти производную данной функции;
2) Определить критические точки данной функции;
3)Из всех критических точек отобрать те, которые лежат внутри заданного отрезка;
4)Выписать значения данной функции в отобранных критических точках;
5)Выписать значения данной функции на концах а и b заданного отрезка;
6) Среди всех указанных вычисленных значений функции определить наименьшие и наибольшие числа. Они и являются решениями поставленной задачи.
Пример : Найдите наименьшее и наибольшее значения функции:


Решение : D ( f )= R
f’ (x) = — 

Найдем критические точки:
f


cos x =0 2sinx — 
x=

sin x =
Х=(-1)


На промежутке (0;

Вычислим значение функции в точке х=
f( 



Вычислим значение функции на концах заданного промежутка:
f (


Из трех значений f (0)=1;
f (
f ( 
Выбираем наименьшее и наибольшее значение
Ответ: min f ( x )= f ( 

Найти наименьшее и наибольшее значение функции: y(x)= -2x

на промежутке: а)
б)
Находим критические точки функции. Т.к. y’(x)= -6x
а) В промежутке 
т.к. y(-2)=8, y(-1)=4, y(-0,5)=3,5 то наименьшее значение функции
y(x)=-2x

в точке x=-2 и равно 8. Кратко запишем так:
б) В промежутке 

Отрезок с концами на сторонах прямого угла содержит точку внутри себя, удаленную на расстоянии 1 и 8 от сторон этого угла.
Найти наименьшую длину таких отрезков.
Р
М
Исходя из того, что
у=
т.к. 
Найдём наименьшее значение функции 

2) Для этого найдём производную
3. Найдём критические точки:





т.к. в точке х = 5 производная меняет свой знак с “-“ на “+”, то это наименьшее значение.
4. 


Ответ: 5
Из круга радиусом R вырезан сектор и из сектора сплетен конус. Каков наибольший объем получившийся конической воронки?


r -радиус основания конуса


Из

V = 

Найдем наибольшее значение функции 


y 2 


y 1 =
Ответ: Наибольший объем равен 
Видео:Задача.Окружность и прямоугольник вписаны в квадрат.Скачать

Прямоугольный участок земли, примыкающий к стене заводского здания, нужно оградить забором. Часть забора, параллельная стене, должна быть каменной, а остальная часть деревянной. Площадь участка 90см. Стоимость 1м каменного забора 10руб, а деревянного 8руб. Найдите такие размеры участка, чтобы стоимость всей ограды была наименьшей?
Р
x (м) — длина каменной части ограды, значит, ширина – 90/х (м),
тогда f ( x )= 10 x +8*2*90/ x = 10 x +1440/ x
2) D (f) =(0; + 
3) f ’ (x)= (10x) + 1440’x – 1440*x/x 2 =
10-1440/ x =10( x 2 -144)/ x 2
4) Найдём критические точки:
f ’ ( x )= 0 10( x 2 -144)/ x 2 =0
D ( f )= (0; + 
В точке x = 12 производная меняет свой знак с – на + , значит это наименьшее значение функции и оно единственное в области определения.
5) м in f (12) =10*12+1440/12=120+120=240
(0;+
Наименьшая длина каменной стены 12 м , а деревянной 90/12=7,5м
Ответ: 12м; 7,5м; 240 руб.
Из всех равнобедренных треугольников, вписанных в данный круг, найдите тот, который имеет наибольшую площадь.
Пусть радиус круга — R , BD =х,

если каждая сторона будет равна 
На изготовление ящика с крышкой расходуется 108 дм 2 фанеры. Стороны основания относятся как 1: 2. Найдите линейные размеры ящика, при которых его объем наибольший.
Решение: S ПОЛН. = 2 ab + 2 ac +2 bc =2( ab + ac + bc )=108
аb-54= — ac-bc

а с=
Пусть а=х, x 


V=a b c= x 2x 









=36- 

V / ( x )=0 36-4 x 




a =3дм , b =6дм, с=
Ответ: 3дм , 6дм , 4дм .
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Задача №6. Найти наибольший объем цилиндра, вписанного в данный конус
Р
Пусть задан конус высотой Н и радиусом основания R .
Обозначим через h высоту цилиндра и через r радиус
основания цилиндра, вписанного в данный конус.
Обозначим ВМ= x . Тогда 
Объём цилиндра 
В нашем случае
Определим, при каком значении x объём цилиндра будет принимать наибольшее значение.
Найдём производную V 1 (x) .
V 1 ( x )=0 при x =
При х 
Следовательно, в точке х= 
V( 

Найти высоту конической воронки наибольшего объёма, если её образующая равна L .
Р
площадь основания которого равна S ,
а высота- Н , вычисляется по формуле 
где 
R — радиус окружности, лежащей в основании конуса.
По теореме Пифагора R и Н связаны равенством R 2 +H 2 =L 2 .
Воспользовавшись этим равенством, выразим V как функцию только одной переменной Н
Решая уравнения 


Из которых точка H принадлежит промежутку (0,L ). При переходе через точку Н 1 функция V / (H) =




Таким образом Н=
Видео:№139. Из некоторой точки проведены к плоскости две наклонные. Докажите, что: а) если наклонные равныСкачать

Задача №8. В трапецию ABCD , боковая сторона АВ , которой
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

(длина 8 см ) перпендикулярна основанию, вписать прямоугольник наибольшей площади так, чтобы одна из его сторон лежала на большем основании трапеции. Основания трапеции равны 6 и 10 см cоответственно. Вычислить площадь этого прямоугольника.
Р
Первый — вершина прямоугольника P лежит на боковой стороне трапеции CD .
Второй — вершина P лежит на основании трапеции ВС .
В первом случае обозначим стороны прямоугольника
Составим уравнение, связывающие неизвестные x и y .
Для этого проведем вспомогательный отрезок BL , параллельный стороне CD и рассмотрим два треугольника ABL и QPD .
Катеты этих треугольников равны соответственно
| AB |=8, | AL |=4, | QD |=10- x , | PQ |= y .
Искомое уравнение получается тогда из условия подобия треугольников ABL и QPD :

Площадь прямоугольника AKPQ равна S ( x )= x (20-2 x ).
Интервал изменения x в первом случае находится из условия, что точка Q — проекция точки P , лежащий на стороне С D , cледовательно, х
Таким образом, задача свелась к отысканию наименьшего значения функции S ( x ) на промежутке [6;10]. Единственная критическая точка функции S ( x ): x =5 не принадлежит найденному промежутку.
Следовательно, производная функции S ( x ) не меняет на этом промежутке знак.
Вычисляя производную S ( x ) в произвольной точке промежутка [6;10] , убеждаемся, что она отрицательна.
Таким образом, наибольшее значение S ( x ) достигается в левом конце промежутка, т.е. max S ( x )= S (6)=48см 2
x 
Площадь прямоугольников, относящихся по второму случаю, не превосходит 48см 2 , т.к. при одинаковой боковой стороне равной 8см , длины их оснований не могут быть больше 6см .
Из квадратного листа жести со стороной а требуется вырезать развертку правильной четырехугольной пирамиды так, чтобы вершины квадрата склеивались в вершину пирамиды. Как это сделать, чтобы получить пирамиду наибольшего объема?
Решение . Пусть АВС D — данный квадрат, О — его центры и KLMN – основание искомой пирамиды. Обозначив через К расстояние от точки К до стороны АВ , выразим объем пирамиды как функцию x .
Получим:
Следовательно,
Функция принимает наибольшее значение одновременно с функцией 




Имеем, V(0)=V(
V(
следовательно, при х= 
Таким образом, объём будет наибольшим тогда, когда диагональ её основания равна 
Видео:Как найти центр круга #2Скачать

Задача № 10. В круг радиуса а вписан равнобедренный треугольник. При каком соотношении сторон треугольник будет иметь наибольшую площадь.

П








Рассмотрим площадь треугольника как функцию переменной а ( 0
S ( a) = 


S` = 

= a 2 ( cos a + 1 ) ( 2cos a – 1 ).
Т.к cos + 1> 0 ( 

Если 0 0, т.е S (a) возрастает на
( 0; 

Вписать в круг радиуса R прямоугольник наибольшей площади.
О

Заметим, что 0 x R , т.к. x -длина хорды окружности радиуса R , отличная от диаметра. Следовательно, площадь прямоугольника 
Hайдем наибольшее значение функции S ( x ) на
Имеем S ’( x )=0 , т.е. 

Значит, надо сравнить значение функции при x = R 
Т.к. S(0)=S(2R)=0, а S(R

в точке x= R
При этом длина другой стороны прямоугольника равна 
Задача № 12. Из всех прямоугольников данного периметра найти тот, у которого диагональ наименьшая.
Пусть периметр прямоугольника равен 2 а и одна из сторон прямоугольника равна х, тогда другая сторона будет
Диагональ прямоугольника — переменная величина, обозначив её через у, получим по теореме Пифагора у 2 =х 2 +(а-х) 2 ,
или у 2 =2х 2 -2ах+а 2 , откуда у=

Производная меняет знак с минуса на плюс на плюс, следовательно, функция х= 
Таким образом, из всех прямоугольников данного периметра наименьшую диагональ имеет квадрат.
Работая над темой «Применение производной к решению экстремальных задач» я изучила очень много литературы по этой теме. При решении задач мне пришлось использовать следующие теоремы:
Необходимый признак возрастания и убывания функции.
Достаточный признак возрастания и убывания функции.
Кроме того «Экстремум функции одной переменной и достаточные условия экстремума функции».
Также я, изучая литературу, выделила этапы решения задач на нахождение промежутков монотонности и экстремумов функции и нахождение наименьшего и наибольшего значений функции на заданном отрезке.
Я считаю, что моя тема очень интересна. Поэтому я буду продолжать ее изучение в дальнейшем.
Моя работа будет очень полезной при подготовке выпускников к экзаменам в качестве дополнительного материала, который можно изучать на факультативах по математике.
1. Кудрявцев В.А., Демидович Б.П.
Краткий курс высшей математики.- М.: Наука,1989
2. Васильев Н.Б. Заочные математические олимпиады. -М.: Наука,1986.
3. Цыпкин А.Г., Пинский А.И. Справочное пособие по методам решения задач по математике.-М.: Наука,1984
4.Крамор В.С. Повторяем и систематизируем школьный курс алгебры и начала анализа.- М.: Просвещение, 1990
5.Шарыгин И.Ф., Голубев В.И. Факультативный курс по математике.-М.: Просвещение,1991
6.Готман Э.Г., Скопец З.А. Решение геометрических задач аналитическим методом -М.: Просвещение, 1979 .
7.Мочалин А.А. Сборник задач по математике.- Саратов, Лицей, 1998.
Видео:Прямоугольник в окружностиСкачать

Четырехугольник, вписанный в окружность — основные свойства, признаки и формулы
Видео:Окружность касается! И ВСЕХ КАСАЕТСЯ!Скачать

Общие сведения
Фигура является вписанной в окружность, когда все ее вершины лежат на ней. Произвести вписание в окружность четырехугольника можно только в том случае, когда он выпуклый. Все его точки находятся по одну сторону от произвольной прямой, которая проходит через соседние вершины фигуры. Нужно отметить, что в этом случае окружность является описанной вокруг фигуры. Если в параллелограмм вписана окружность, то ее центр совпадает с центром окружности, которая описана вокруг него.
Четырехугольники бывают самопересекающимися. Они также могут быть вписанными, однако это встречается крайне редко. Не каждую фигуру можно вписать в круг, поскольку существуют определенные законы. Например, вокруг ромба нельзя описать круг — исключение составляет случай, когда ромб является квадратом.
Основные правила
Выпуклый четырехугольник можно вписать в окружность. Однако для этого существуют некоторые правила (критерии) или признаки. Некоторые задачи сформулированы таким образом, что нужно знать основные критерии, а также уметь доказывать возможность вписывать или описывать окружность. Около четырехугольника можно описать окружность, если выполняются следующие условия:
- Сумма углов, которые являются противоположными, соответствует 180 градусам.
- Соблюдается равенство смежного и противоположного углов.
- Угол между стороной и диагональю равен углу между противоположной стороной и диагональю.
- Произведение двух диагоналей соответствует размерности суммы произведений противоположных сторон.
- Четыре точки лежат на окружности, когда две прямые АС и BD, образующие диагонали, пересекаются в некоторой точке P, а также выполняется следующее равенство: AP * PC = BP * PD.
- Произведения тангенсов половины двух противоположных углов равны 1. Кроме того, значения произведений эквивалентны друг другу (tg (A/2) * tg (C/2) = tg (B/2) * tg (D/2) = 1).
Четвертое утверждение является теоремой Птолемея. Все эти правила являются следствиями, полученными при доказательстве различных гипотез. Правила можно применять в зависимости от условия поставленной задачи. Любой параллелограмм можно вписать в окружность, когда он является прямоугольником или квадратом.
Свойства и утверждения
При решении можно воспользоваться некоторыми свойствами, которые были доказаны. Это нужно для того, чтобы не тратить время на выведение какой-либо формулы. Применяется методика для оптимизации вычислений. К ним можно отнести следующие:
- Если вокруг четырехугольника описана окружность, то центры окружностей, которые вписанных в треугольники, образованные диагоналями фигуры, являются вершинами прямоугольника.
- Не бывает четырехугольников, вписанных в окружность, с рациональной площадью и сторонами, которые образуют арифметический или геометрический тип прогрессии.
- При продолжении сторон до точек пересечения Y и Z, внутренние биссектрисы углов Y и Z являются перпендикулярными.
Данные утверждения применяются не всегда. В некоторых случаях можно ограничиться формулами и основными соотношениями — они позволяют легко и быстро искать нужные величины.
Видео:№138. Из некоторой точки проведены к данной плоскости перпендикуляр и наклонная, угол между которымиСкачать

Формулы и соотношения
Очень часто необходимо перерыть горы информации для поиска нужной формулы. Это сказывается на оптимизации решения. Кроме того, некоторые соотношения могут содержать ошибки, поскольку материал излагается неквалифицированными специалистами.
Педагоги утверждают, что обучение какой-либо дисциплине с физико-математическим уклоном должно быть основано на алгоритмах. Кроме того, рекомендуется прочитать условие задачи несколько раз до полного его понимания. В основном необходимо находить площадь, диагонали и углы четырехугольника.
Периметр и полупериметр
Периметром выпуклого четырехугольника со сторонами a, b, c и d называется сумма длин всех его сторон. Величина обозначается литерой «Р», и вычисляется по следующей формуле: P = a + b + c +d. Кроме того, в некоторых формулах встречается величина, которая называется полупериметром. Обозначается она литерой «р». Для ее нахождения применяется такое соотношение: p = P / 2 = (a + b + c +d) / 2. Единицей измерения полупериметра являются метрические величины: мм, см, дм, м и т. д.
Для квадрата формула периметра имеет вид: P = 4 * a. Равенство легко доказывается для фигуры со стороной а. Из определения периметра получается соотношение: P = a + a + a + a. Если привести подобные слагаемые, то результирующая формула имеет вид: P = 4 * a. У прямоугольника противоположные стороны равны. Чтобы найти его периметр, нужно воспользоваться равенством: P = a + b + a + b = 2 * (a + b). Необходимо отметить, что квадрат является правильным четырехугольником, поскольку его стороны равны между собой.
Понятие площади
Площадь двумерных фигур — понятие геометрии, которое показывает ее численную характеристику или размер. Очень часто она обозначается литерой S. Измеряется величина в квадратных единицах (см 2 , м 2 и т. д. ). Фигура, имеющая характеристику S, называется квадратируемой.
Для нахождения S применяется интегральный метод, но существуют частные случаи, при которых интегрировать необязательно. Очень часто возникает необходимость перевода одной единицы в другую. Для этого существует простой алгоритм, позволяющий корректно выполнить данную операцию. Например, нужно перевести м 2 в см 2 . Необязательно заучивать единицы площади и их эквивалентность другим. Достаточно выполнить следующие действия:
- Определить базовую единицу: м и см.
- Выполнить перевод одной метрической величины в другую: 1 м = 100 см.
- Возвести обе части выражения во втором пункте в квадрат: 1 м 2 = 100 2 см 2 = 10000 см 2 .
Однако бывают и другие единицы, которые применяются для измерения размерности земельных участков: 1 ар (сокращенно а) = 1 сотке = 100 м 2 и 1 гектар (га) = 10000 м 2 .
Когда известны все стороны четырехугольника (a, b, c и d), который вписан в окружность, можно найти его S. Для этого нужно знать еще одну величину. Она называется полупериметром. Расчет выполняется по формуле: S = [(p — a) * (p — b) * (p — c) * (p — d)]^(½). Соотношение называется формулой Брахмагупты.
Необходимо отметить, что вписанный четырехугольник обладает максимальным значением S среди остальных эквивалентных фигур. Если известны четыре стороны, которые являются последовательными (a, b, c и d), а также угол В между a и b, то можно воспользоваться более упрощенной формулой: S = [(a * b + c * d) * sin (B)] / 2. В случае, когда известны все стороны и любой угол (Y) между диагоналями, соотношение можно записать таким образом: S = [(a * с + и * d) * sin (Y)] / 2.
Площадь можно выразить и другим соотношением, когда известны все стороны и угол А, который не является прямым: S = [(a 2 — b 2 — c 2 + d 2 ) * tg (A)] / 4. При известном радиусе описанной окружности и углах (A, B и Y) можно воспользоваться такой формулой: S = 2 * R^(2) * sin (A) * sin (B) * sin (Y). Следствием из последнего соотношения является S 2 . Если четырехугольник является квадратом, то неравенство преобразуется в равенство, т. е. S = 2 * R 2 .
Диагонали и углы
Для вписанного четырехугольника ABCD существуют определенные соотношения, по которым можно найти его диагонали. Для фигуры со сторонами a = AB, b = BC, c = CD и d = DA диагонали (s = АС и t = DA) находятся таким образом: s = [((a * c + b * d) * (a * d + b * c)) / (a * b + c * d)]^(½) и t = [((a * c + b * d) * (a * b + d * c)) / (a * d + c * b)]^(½). Если умножить диагональ s на t и привести подобные слагаемые, то в результате получится формула Птолемея: s * t = a * c + b * d.
При отношении двух диагоналей получается вторая теорема Птолемея: s / t = (a * d + b * c) / (a * b + d * c). Сумма диагоналей — есть неравенство такого вида: s + t >= 2 * [a * c + b * d]^(½). Неравенство преобразуется в равенство, когда диагонали равны. Однако в этом случае можно воспользоваться следующим выражением: [s + t]^(½) >= [a * c]^(2) + [b * d]^(2).
Необходимо отметить, что в произвольном выпуклом четырехугольнике диагонали делят его на 4 треугольника, которые являются между собой подобными по парам. Кроме того, при пересечении двух диагоналей AC и BD в некоторой точке М, справедливо следующее соотношение: AM / CM = (AB * AD) / (CB * CD).
Можно находить и некоторые углы фигуры. Для этого существуют определенные соотношения. Во вписанном четырехугольнике со сторонами, которые соответствуют значениям a, b, c и d, углом A между сторонами a и d, а также полупериметром p, функции тригонометрического типа для А вычисляются таким образом:
- cos (A) = (a 2 + d 2 — b 2 — c 2 ) / (2 * (a * d + b + c)).
- sin (A) = [(p — a) * (p — b) * (p — c) * (p — d)]^(½) / (a * d + b + c).
- tg (A/2) = [((p — a) * (p — d)) / ((p — b) * (p — c))]^(½).
В некоторых случаях нужно вычислить значение тангенса для угла Y, который находится между диагоналями, по формуле: tg (Y/2) = [((p — b) * (p — d)) / ((p — a) * (p — c))]^(½).
В геометрии существует вписанный четырехугольник, стороны которого являются целыми числами. Кроме того, целочисленными являются также его диагонали и площадь. Он называется четырехугольником Брахмагупты. Однако для преобразования любого четырехугольника в данную фигуру необходимо выполнить некоторые математические операции. Пусть он имеет следующие целочисленные параметры:
- Стороны: a, b, c и d.
- Диагонали: s и t.
- Площадь: S.
- Радиус описанной окружности: R.
В некоторых случаях возникает необходимость избавиться от рациональных значений в знаменателе. При значениях дробных параметров k, l и m нужно использовать такие соотношения:
- a = [k * (l + m) + (1 — (l * m))] * [l + m — k * (1 — (l * m))].
- b = (1 — l 2 ) * (m — k) * (1 + k * m).
- c = k * (1 + l 2 ) * (1 + m 2 ).
- d = (1 + m 2 ) * (l — k) * (1 + k * l).
- s = l * (1 + k 2 ) * (1 + m 2 ).
- t = m * (1 + k 2 ) * (1 + l 2 ).
- S = l * m * [2 * k * (1 — l * m) — (l + m) * (1 — k 2 )] * [2 * k (l + m) + (1 — l * m) * (1 — k 2 )].
- 4 * R = (1 + l 2 ) * (1 + m 2 ) * (1 + k 2 ).
Существуют также соотношения для описанной вокруг четырехугольника окружности. Математики утверждают, что при комбинации двух и более геометрических фигур время поиска некоторых параметров увеличивается.
Параметры для окружности
Радиус окружности R для четырехугольника c полупериметром р и со сторонами a, b, c, d находится по формуле Парамешвары: R = (¼) * [((a * b + c * d) * (a * c + b * d) * (a * d + b * c)) / ((p — a) * (p — b) * (p — c) * (p — d))]^(½). Соотношение было выведено в XV веке математиком из Индии Ватассери Парамешварой.
При комбинации данной формулы с соотношением Брахмагупты можно получить следующее соотношение: 4 * S * R = [(a * b + c * d) * (a * c + b * d) * (a * d + b *c)]^(½). Следует отметить, что величина S является площадью вписанного четырехугольника. Для ортогонального четырехугольника с перпендикулярными диагоналями, которые делятся на отрезки s1, s2, t1 и t2, существует некоторое соотношение, позволяющее найти диаметр окружности (D): D 2 = (s1)^2 + (s2)^2 + (t1)^2 + (t2)^2 = a 2 + c 2 = b 2 + d 2 .
Радиус в этом случае находится таким образом: R = D / 2 = [(s1)^2 + (s2)^2 + (t1)^2 + (t2)^2] / 2 = [a 2 + c 2 ] / 2 = [b 2 + d 2 ] / 2. Если выполнить сложение квадратов сторон, то получится такое равенство: 8 * R = a 2 + b 2 + c 2 + d 2 . По формуле Эйлера R можно также выразить через диагонали (s и t) и расстояние v между их серединами: R = [(s 2 + t 2 + 4 * v 2 ) / 8]^(½).
Таким образом, специалисты рекомендуют на начальных этапах обучения использовать уже готовые формулы для вычисления основных параметров выпуклого четырехугольника, вписанного в окружность.
🎬 Видео
Геометрия. ОГЭ по математике. Задание 16Скачать

Прямоугольник, вписанный в окружность.Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Три окружности в прямоугольнике.Скачать
11 класс, 43 урок, Вписанный четырехугольникСкачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать