Задача площадь прямоугольного треугольника

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

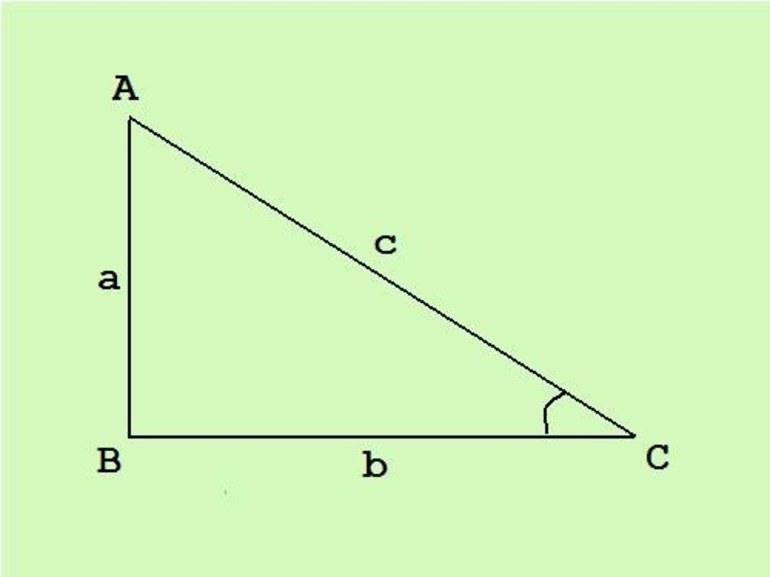
Свойства треугольника

Пожалуй, в жизни любой человек сталкивается с треугольниками. Они бывают разными: остроугольными, тупоугольными, прямоугольными, равнобедренными и равносторонними. Но всех их объединяет один признак — существование трёх углов. Точное определение фигуре дали ещё в Древней Греции. Евклид утверждал, что этот объект состоит из трёх точек, расположенных на разных прямых, и трёх замкнутых линий, поочерёдно соединяющих эти точки.

Три точки, ограничивающие отрезки, называют вершинами, а линии, соединяющие их, — сторонами. Внутреннюю плоскость, заключённую в линии, называют площадью. Так как отрезки фигуры образуют три угла, то объект относится к классу многоугольников. Замкнутая прямая, соединяющая вершину с серединой противолежащей стороны, носит имя медиана. Всего их может быть три штуки, пересекаться они могут в одной точке, которую называют центроидом. Он является центром тяжести.

Если из угла провести перпендикуляр к противолежащей стороне, то полученная линия будет высотой. Линия, опущенная к стороне напротив угла и разделяющая его пополам, называется биссектрисой. В любой треугольник можно вписать окружность. Она будет единственной, так как должна касаться всех трёх сторон. Центр круга всегда будет совпадать с местом пересечения биссектрис.

Разделение треугольников происходит по размерам углов и сторон. Например, у равносторонней фигуры любой из трёх углов равен 60 градусам, у равнобедренной — две стороны и два угла равны. Для любого треугольника справедливо утверждать следующее:

• всегда напротив длинной стороны будет находиться больший угол;
• если две стороны равны, то напротив них будут равные углы;
• при сложении значений всех углов сумма составит 180 градусов;
• продолжив сторону за пределы объекта, можно получить внешний угол;
• одна из сторон всегда будет меньше суммы оставшихся и больше их разности.

В элементарной математике часто используют правила, называемые признаками подобия и равенства. Так, при сравнении две фигуры будут равными, если длины их сторон совпадают. Соответственно, углы тоже станут одинаковыми или будут равными две стороны и угол между ними.

Видео:Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

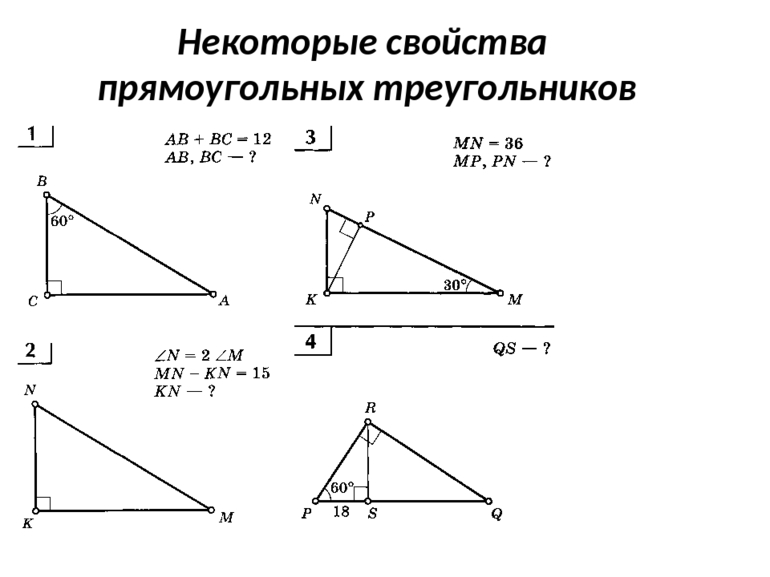
Прямоугольная фигура

Треугольник с одним прямым углом, то есть составляющим 90 градусов, называется прямоугольным. Два отрезка, примыкающие к нему, называют катетами, а прямую, соединяющую их, — гипотенузой. Из любого треугольника можно получить две прямоугольных фигуры. Для этого нужно в нём опустить высоту. Многие свойства многоугольника идентичны прямоугольной фигуре. Два равных треугольника можно объединить в прямоугольник, при этом их гипотенузы будут совпадать с диагональю.

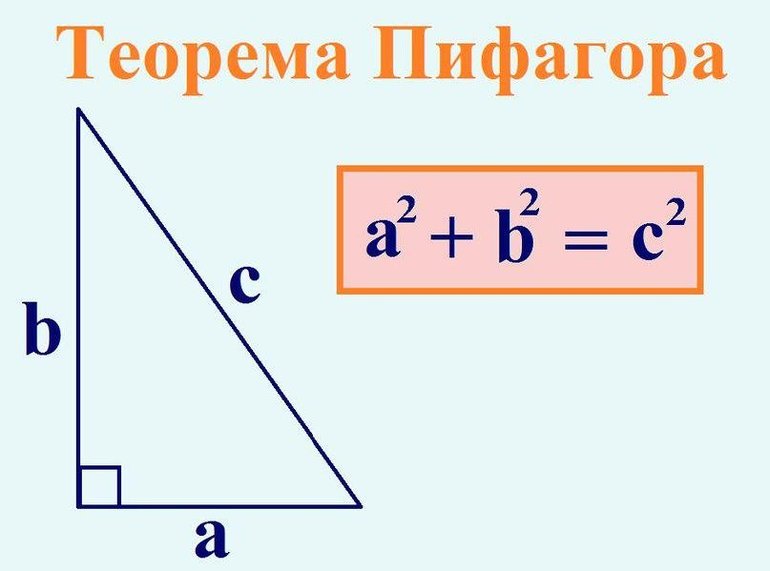
Основную особенность фигуры, которая позволяет посчитать площадь, подметил ещё Пифагор. Она очень простая и записывается как с 2 = а 2 + b 2 . В соответствии с этим правилом квадрат гипотенузы равняется результату сложения квадратов катетов, то есть сумма площадей квадратов, достроенных на катетах, совпадает с площадью квадрата, построенного на гипотенузе. Кроме основного свойства, чтобы найти площадь прямоугольного треугольника, нужно знать следующие правила:

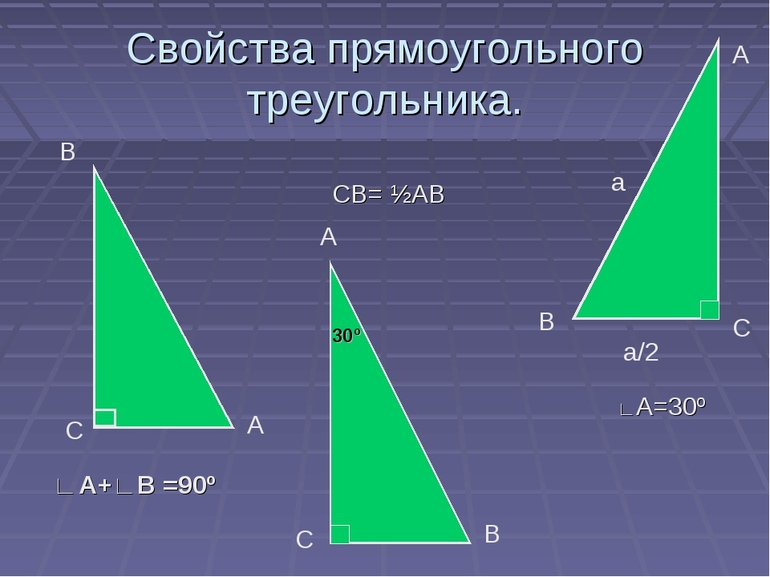
• при сложении двух острых углов сумма будет равняться 90 градусов;
• гипотенуза у фигуры всегда будет больше катета;
• длину катета, расположенного напротив угла в 30 градусов, можно найти, разделив гипотенузу пополам;
• катеты в прямоугольном треугольнике одновременно являются его высотами;
• величина радиуса описанной окружности совпадает с медианой.

Из теоремы Пифагора можно сделать важное следствие. Становится очевидным, что высота, опущенная из прямого угла, разделит гипотенузу на два отрезка: c1 = a2/c и c1 = b2/c. Полученные замкнутые линии являются проекциями катетов. В то же время высоту фигуры можно определить, используя следующую формулу: h = √ca + cb.

Если угол, располагающийся напротив катета a, обозначить альфой, а напротив b — бетой, то справедливо утверждать, что гипотенуза будет равняться: c = b /sin b = a / sin a = b / cos a = a / cos b = h = √a 2 + b 2 . Другими словами, длины катетов можно вычислить, используя синус противолежащего угла или косинус прилежащего. То есть получатся равенства: a = c * sin a = c * cos b и b = c * cos a = c * sin b. Учитывая тригонометрические правила, катеты можно найти, используя тангенс. Так, сторона b = a * tg b, катет a = b * tg a.

Все рассмотренные формулы и свойства помогают при нахождении площади фигуры. Но кроме них полезно знать и то, что радиус вписанной окружности в прямоугольную фигуру можно узнать, найдя разницу суммы катетов и гипотенузы, разделённую на 2, то есть r = (a + b — c) / 2.

Видео:Найдите площадь прямоугольного треугольника, если сумма его катетов равна 15, а гипотенуза равна 13Скачать

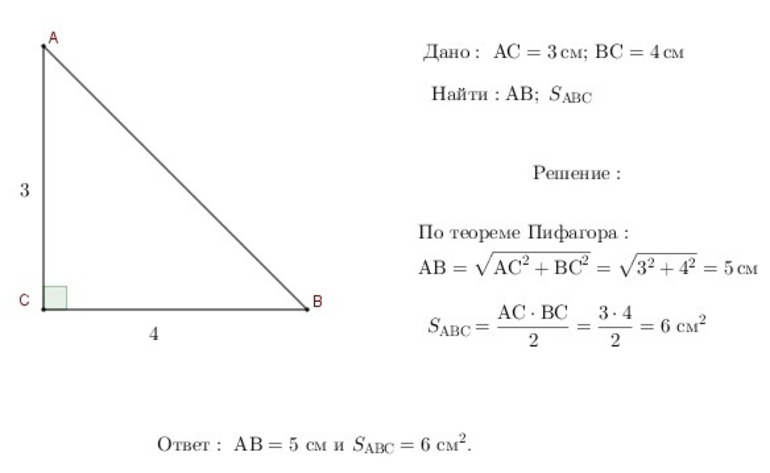
Формулы площади

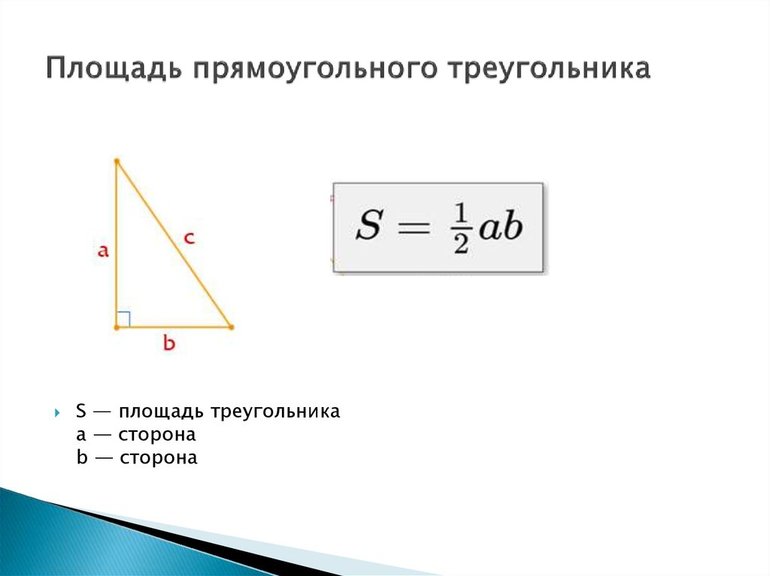
Найти площадь треугольника с прямым углом можно различными способами. Но проще всего это сделать через катеты. Выражение для нахождения параметра довольно простое: S = (a * b) / 2. Это классическая формула площади прямоугольного треугольника. Существуют и другие формулы:

• S = (a 2 * tg b) / 2;
• S = (a 2 * ctg a) / 2;
• S = (b 2 * tg a) / 2;
• S = (b 2 * ctg b) / 2.

Другими словами, площадь можно определить, зная значения двух катетов, длину одного из них и разворот противолежащего или прилежащего угла. Для доказательства теоремы нахождения площади понадобится изобразить фигуры с катетами b и a. Фигуру можно достроить до параллелограмма, отложив параллельные катетам прямые. Вершины полученного объекта можно обозначить буквами A, B, C, D, начиная с прямого угла треугольника и двигаясь влево.

Прямоугольник образуется двумя треугольниками, равными между собой по трём сторонам: AB = CD, AC = BD (ВС — общая сторона). Учитывая равенства, можно утверждать, что площади фигур равны друг другу. Следовательно, площадь параллелограмма можно найти через сумму площадей двух треугольников: S = Sabc + Sacd. Отсюда верным будет утверждение, что площадь начального треугольника ABC равняется половине замкнутой области прямоугольника, а та соответствует произведению сторон: S = a * b, то есть AB * BC.

Эта формула легко доказывается с учётом того, что прямоугольник является фигурой, в которую можно вписать несколько четырёхугольников. Так как общая площадь будет равняться сумме площадей внутренних фигур, то верным будет равенство: (a + b)2 = S + S + a2 + b2 = a2 + 2ab + b2 = 2S + a2 + b2. Отсюда получим, что S = a* b. Следовательно, так как площадь треугольника равняется половине площади прямоугольной фигуры, то можно утверждать, что S = (a * b)/2 = (AB * BC) / 2. Формула доказана.

Из этого правила вытекают два следствия:

• площадь равняется половине результата перемножения катетов;
• когда высоты двух треугольных фигур совпадают, их площади можно соотнести как основания.
• если угол одного треугольника равен углу другого, то площади объектов соотносятся как результат умножения сторон с одинаковыми углами.

Использование рассмотренных следствий помогает при решении многих геометрических задач. Они касаются не только треугольников, но и других многоугольных фигур.

Видео:Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Решение задач

Важно не только знать формулы для нахождения площади, но и уметь их применять на практике. Это возможно лишь с опытом, который можно получить, решая различные задания. Существуют определённые задачи, которые ученикам нужно решить самостоятельно. После успешного решения можно утверждать, что учащиеся полностью разобрались в теме, поэтому они могут переходить к следующему разделу геометрии. Вот некоторые задания, позволяющие закрепить теоретический материал:

1. В прямоугольнике одна из сторон равна 35 см, а другая — 50 см. Нужно найти площадь фигур, полученных в результате проведения диагонали. В соответствии с правилом диагональ прямоугольника разделяет его на два равных прямоугольных треугольника, при этом его стороны являются катетами полученных фигур. Отсюда следует, что S1 = S2 = a * b / 2 = 35 * 50 / 2 = 1750 / 2 = 875 см².
2. Есть прямоугольный треугольник, катет которого равняется 15 см, а гипотенуза — 25 см. Нужно вычислить площадь фигуры. Для решения задачи следует узнать длину второго катета. Сделать это удастся, используя формулу гипотенузы: c = √a2 + b2. Из неё можно выразить неизвестный катет. Его длина будет равняться: b = √c2 — a2 = √252 — 152 = √625 — 225 = √400 = 20 см. Известные данные нужно подставить в формулу площади и выполнить расчёт: S = 20 * 15 / 2 = 150 см².

Длина катета в треугольнике равна 2 * √3 см, а противолежащий ему угол составляет 50 градусов. Необходимо вычислить площадь фигуры. Известно, что сумма углов в таком треугольнике — 180 градусов. Следовательно, разворот прилежащего к катету углу равняется a = 180 — 90 — b = 180 — 90 — 60 = 30 градусов. Теперь можно использовать формулу для нахождения площади прямоугольного многоугольника через катет и тангенс угла: S = (b 2 * tg a) / 2 = ((2 * √3) 2 * tg 30) / 2 = (12/2) * (√3/3) = 2√3 см 2 .

Таким образом, площадь прямоугольной фигуры — ее численная характеристика. Определить ее можно, используя несколько способов. При этом всегда необходимо знать длину хотя бы одного из катетов. Это связанно с тем, что две из трёх высот совпадают с ним.

Видео:Задача, которую исключили из экзамена в АмерикеСкачать

Задачи по теме «Площадь треугольника»
методическая разработка по геометрии (9 класс)

Задачи на нахождение площади треугольника, возможно использовать при подготовке к ОГЭ

Видео:Геометрия 8 класс : Задача на площадь прямоугольного треугольника и на соотношение площадейСкачать

Скачать:

Видео:4 класс, 25 урок, Площадь прямоугольного треугольникаСкачать

Предварительный просмотр:

1. Площадь прямоугольного треугольника равна 69, а один из катетов равен 23. Найти другой катет.

2. Угол при вершине, противолежащей основанию равнобедренного треугольника равен 150º. Найти площадь этого треугольника, если боковая сторона равна 28.

3. Боковая сторона равнобедренного треугольника равна 35, а основание 42. Найти площадь этого треугольника.

4. Найти площадь равностороннего треугольника со стороной, равной 4.

5. Найти площадь треугольника со сторонами 6, 6, 8.

1. Боковая сторона равнобедренного треугольника равна 25, а основание 30. Найти площадь этого треугольника.

2. Найти площадь треугольника со сторонами 5, 7, 6.

3. Найти площадь равностороннего треугольника со стороной, равной 10.

4. Угол при вершине, противолежащей основанию равнобедренного треугольника равен 150º. Найти площадь этого треугольника, если боковая сторона равна 44.

5. Площадь прямоугольного треугольника равна 75, а один из катетов равен 15. Найти другой катет.

1. Найти площадь равностороннего треугольника со стороной, равной 6.

2. Боковая сторона равнобедренного треугольника равна 50, а основание 60. Найти площадь этого треугольника.

3. Площадь прямоугольного треугольника равна 224, а один из катетов равен 28. Найти другой катет.

4. Найти площадь треугольника со сторонами 6, 4, 8.

5. Угол при вершине, противолежащей основанию равнобедренного треугольника равен 150º. Найти площадь этого треугольника, если боковая сторона равна 26.

1. Угол при вершине, противолежащей основанию равнобедренного треугольника равен 150º. Найти площадь этого треугольника, если боковая сторона равна 34.

2. Найти площадь равностороннего треугольника со стороной, равной 8.

3. Найти площадь треугольника со сторонами 8, 5, 7.

4. Площадь прямоугольного треугольника равна 273, а один из катетов равен 39. Найти другой катет.

5. Боковая сторона равнобедренного треугольника равна 52, а основание 96. Найти площадь этого треугольника.

Видео:Геометрия 8. Урок 14 - Площадь треугольников. Формулы и задачи.Скачать

Банк разноуровневых задач по теме «Площадь треугольника»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:8 класс, 14 урок, Площадь треугольникаСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Банк разноуровневых задач по теме «Площадь треугольника»

Выполнила; Лепехина Диана

I уровень

Сторона треугольника равна 5 см, а высота, проведенная к ней, в три раза больше стороны. Найдите площадь треугольника.

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.).

Ответ дайте в квадратных сантиметрах.

Найдите площадь треугольника, вершины которого имеют координаты (1; 6), (9; 6), (9; 9).

Найдите площадь равнобедренного прямоугольного треугольника с катетом равным 15 см.

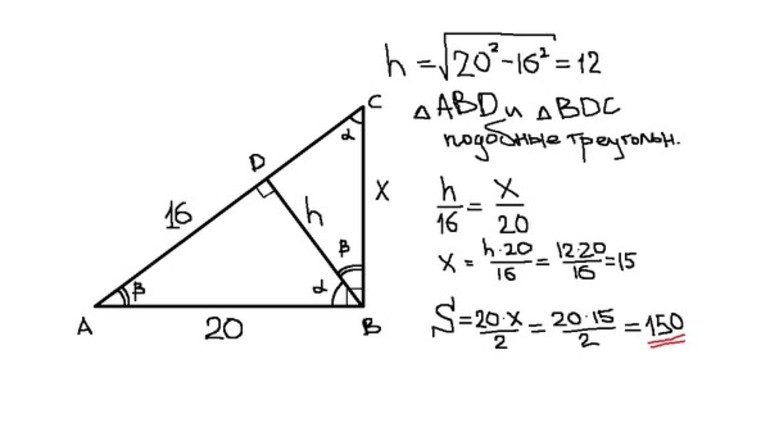
Найдите площадь прямоугольного треугольника, если его высота делит гипотенузу на отрезки 32 см и 18 см.

В ∆АВС угол А равен 45˚, ВС=10 см, а высота В D делит сторону АС на отрезки AD =6 см, DC =8 см. Найдите площадь ∆АВС и высоту, проведённую к стороне ВС.

Известно, что точки K и L лежат соответственно на сторонах AB и BC

треугольника ABC, а точка O – точка пересечения AL и KC. Известно, что площади треугольников AOK и COL равны соответственно 1 и 8, а

треугольник AOC и четырехугольник BKOL равновелики. Найти

площадь треугольника AOC.

Внутри параллелограмма выбрана произвольная точка и проведены отрезки и . Площади трех из образовавшихся треугольников равны 1, 2 и 3. Какие значения может принимать площадь четвертого треугольника?

Треугольник АВС, АС = 5 см

Высота ВН в два раза больше стороны АС.

Найти S треугольника АВС.

Найдем длину высоты ВН = 2 АС

Чтобы найти площадь любого треугольника, нужно найти произведение половины высоты на сторону, к которой эта высота проведена.

Тогда площадь треугольника АВС находиться по формуле:

S = 1/2  10 5 = 5  5 = 25

2) AC =6см;А H =3см

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию или его продолжению. Поэтому

3) AC (основание)=9-1=8

Площадь прямоугольного треугольника равна половине произведения катетов

1) Обозначим катеты треугольника как x , значит:

Пусть в треугольнике АВС, ∠ С = 90°, CD — высота, AD = 32 см, DB = 18см. Найти S _{∠ АВС} .

Рассмотрим треугольник ABD:

∠ A =45 следовательно ∠ ABD =45 и треугольник равнобедренный BD=AD=6.

S = высотусторону на которую опущена высота

Высота, проведённая к стороне BC= = 8,4см

BC найдено по площади треугольника

Ответ: S = 42 BC = 8,4 см

Также заметим , что

Ответ: 6

3)Сделаем рисунок и обозначим площади, например, так:

Тогда

Если площади «распределены» по-другому,

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 937 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 681 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 305 человек из 67 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 497 855 материалов в базе

Видео:Площадь прямоугольного треугольника равна 200√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Дистанционные курсы для педагогов

Другие материалы

• 04.09.2020
• 506

• 03.09.2020
• 300

• 03.09.2020
• 1297

• 03.09.2020
• 926

• 03.09.2020
• 224

• 03.09.2020
• 162

• 03.09.2020
• 147

• 03.09.2020
• 1150

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 04.09.2020 760 —> —> —> —>
• DOCX 135 кбайт —> —>
• Оцените материал:

Настоящий материал опубликован пользователем Лепехина Диана Сергеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 2 года и 1 месяц
• Подписчики: 0
• Всего просмотров: 5965
• Всего материалов: 10

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Найдите площадь прямоугольного треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Онлайн-семинар о снятии эмоционального напряжения у детей и подростков

Время чтения: 2 минуты

Опубликованы проекты ФГОС по специальностям СПО

Время чтения: 2 минуты

Каждый второй российский студент недоволен своим вузом

Время чтения: 1 минута

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

«Учителя года» проведут открытые занятия для педагогов России

Время чтения: 1 минута

В Сыктывкаре школьников переведут на дистанционное обучение

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🌟 Видео

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

КАК НАЙТИ ПЛОЩАДЬ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать

Задача #22 Найдите площадь прямоугольного треугольника.Скачать

Урок 38. Площадь треугольника, прямоугольного треугольника, ромбаСкачать

№471. Найдите площадь прямоугольного треугольника, если его катеты равны: а) 4 см и 11см;Скачать

Найти площадь треугольника АВС. Задачи по рисункамСкачать

Площадь прямоугольного треугольника равна (242√3)/3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Площадь прямоугольного треугольника равна 364,5∙√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать