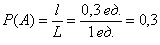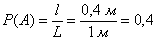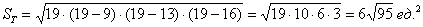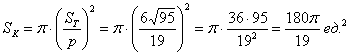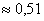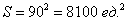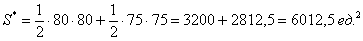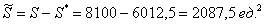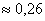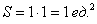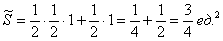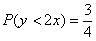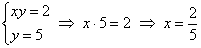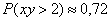Задача на вероятность треугольника (7 видео)

1.5. Геометрическое определение вероятности

Классическое определение вероятности оказывается эффективным для решения целого спектра задач, но с другой стороны, обладает и рядом ограничений. Одним из таких ограничений является тот факт, что оно неприменимо к испытаниям с бесконечным количеством исходов. Простейший пример:

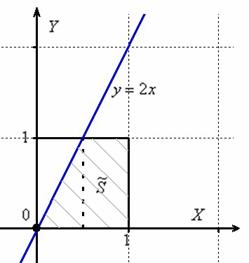
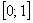
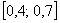
На отрезок наудачу бросается точка. Какова вероятность того, что она попадёт в промежуток ?

Поскольку на отрезке бесконечно много точек, то здесь нельзя применить формулу 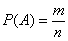(ввиду бесконечно большого значения «эн») и поэтому на помощь приходит другой подход, называемый геометрическим определением вероятности:

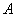
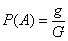
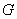
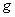
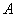
Вероятность наступления некоторого события в испытании равна отношению , где – геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а – мера, выражающая количество благоприятствующих событию исходов.

На практике в качестве такой геометрической меры чаще всего выступает длина или площадь, реже – объём.
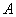
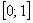
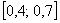
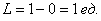
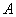
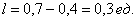
Рассмотрим событие: – брошенная на отрезок точка, попала в промежуток . Очевидно, что общее число исходов выражается длиной бОльшего отрезка: , а благоприятствующие событию исходы – длиной вложенного отрезка: По геометрическому определению вероятности:

Примечание: 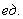– метрические единицы: метры, сантиметры или какие-то др.

Слишком просто? Как и в случае с классическим определением, это обманчивое впечатление. Обстоятельно и добросовестно разбираемся в практических примерах:

Задача 28
Метровую ленту случайным образом разрезают ножницами. Найти вероятность того, что длина обрезка составит не менее 80 см.

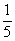
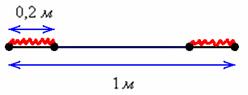
Решение: «чего тут сложного? Вероятность равна ». Это автоматическая ошибка, которую допускают по небрежности. Да, совершенно верно – длина обрезка составит не менее 80 см, если от ленты отрезать меньше 20 сантиметров. Но здесь часто забывают, что искомый разрез можно сделать как с одного конца ленты, так и с другого:

Рассмотрим событие: 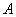– длина обрезка составит не менее 0,8 м.

Поскольку ленту можно разрезать где угодно, то общему числу исходов соответствует её длина: 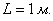Благоприятствующим исходам соответствуют участки, отмеченные красным цветом, и их суммарная длина равна:
По геометрическому определению:

Ответ: 0,4

Какой можно сделать вывод?

Даже если задача кажется вам очень простой, НЕ СПЕШИТЕ

При оформлении задач следует обязательно указывать размерность (единицы, метры, квадратные единицы, квадратные метры и т.д.). Кстати, обратите внимание, что на финальном этапе вычислений геометрическая мера сокращается. Так в рассмотренном примере, сократились метры: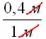
, в результате чего получилась привычная безразмерная вероятность.

Следующая задача для самостоятельного решения:

Задача 29
После бури на участке между 40-м и 70-м километрами телефонной линии произошёл обрыв провода. Какова вероятность того, что он произошёл между 50-м и 55-м километрами линии?

Значительно чаще встречаются примеры, в которых фигурируют площади:
Задача 30
В треугольник со сторонами 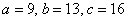вписан круг. Точка произвольно ставится в треугольник. Найти вероятность того, что точка попадёт в круг.

Вспоминаем геометрию: вписанный круг лежит внутри треугольника и касается его сторон в трёх точках. …Представили? Отлично!

Решение: поскольку точка ставится в треугольник, а круг лежит внутри, то общему числу исходов соответствует площадь треугольника, а множеству благоприятствующих исходов – площадь вписанного круга.

Осталось вспомнить или отыскать (проще всего в Сети) школьные геометрические формулы. Если даны длины сторон треугольника, то его площадь удобно найти по формуле Герона: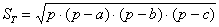
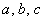
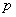
, где – длины сторон треугольника, а – полупериметр.

Сначала вычислим полупериметр треугольника: 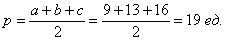, а затем его площадь:

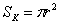
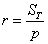
Площадь круга найдём по известной формуле . Если круг вписан в треугольник, то его радиус можно рассчитать по формуле , этого я не вообще не знал – только что нашёл в Интернете.

Итак, площадь вписанного круга:

По геометрическому определению:
– вероятность того, что точка попадёт во вписанный круг.

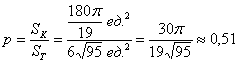
Ответ:

Более простой пример для самостоятельного решения:

Задача 31
В круге радиуса 10 см находится прямоугольный треугольник с катетами 12 и 7 см. В круг наудачу ставится точка. Найти вероятность того, что она не попадёт в данный треугольник.

Следует отметить, что в этой задаче треугольник вовсе не обязан как-то касаться окружности, он просто расположен внутри круга и всё. Будьте внимательны!

А теперь рассмотрим широко известную задачу о встрече:

Задача 32
Две грузовые машины могут подойти на погрузку в промежуток времени от 19.00 до 20.30. Погрузка первой машины длится 10 минут, второй – 15 минут. Какова вероятность того, что одной машине придется ждать окончания погрузки другой?

Решение: сначала выясним длительность временнОго промежутка, на котором могут пересечься автомобили: это 90 минут (коль скоро, от 19.00 до 20.30). Изобразим прямоугольную систему координат, где в подходящем масштабе построим квадрат размером 90 на 90 единиц: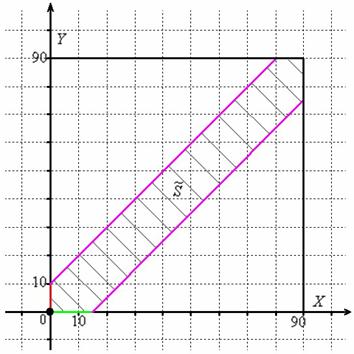

Общему множеству исходов соответствует площадь данного квадрата:

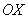
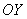
Далее по оси от начала координат откладываем время погрузки одного автомобиля (зелёная линия), а по оси – время погрузки другого автомобиля (красная линия) (можно наоборот, это не повлияет на решение).

Теперь из правого конца зелёного отрезка и из верхнего конца красного отрезка под углом 45 градусов проводим две линии внутри квадрата (малиновые отрезки).

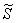
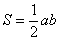
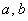
Множеству благоприятствующих исходов (когда автомобили «пересекутся» во времени) соответствует площадь заштрихованной фигуры. В принципе, её можно вычислить «на пальцах», но технически проще использовать окольный путь, а именно, вычислить площади двух прямоугольных треугольников. Используем формулу:
, где – длины катетов.

В нашей задаче: верхний треугольник имеет катеты длиной по 80 единиц, нижний треугольник – по 75 единиц. Обратите внимание, что в общем случае эти треугольники не равны.

Таким образом, суммарная площадь треугольников составляет:

И бесхитростный заключительный манёвр: из площади квадрата вычитаем площади треугольников, получая тем самым благоприятствующую площадь:

По геометрическому определению:
– вероятность того, что одной машине придется ждать окончания погрузки другой.

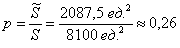
Ответ:

Подробное объяснение этого способа решения можно найти, например, в учебном пособии В.Е. Гмурмана, я же остановился лишь на техническом алгоритме, дабы не тратить ваше драгоценное время.

И если в разобранной задаче встреча явно нежелательна, то в следующей, скорее, наоборот. Романтичный эпизод для самостоятельного изучения:

Задача 33
Студенты случайным образом приходят в столовую с 14.00 до 15.00, при этом обед каждого из них занимает примерно 20 минут. Найти вероятность того, что: а) Коля встретится с Олей во время обеда, б) данная встреча не состоится.

Не нужно печалиться по поводу пункта «бэ» – любовь приходит и уходит, а кушать хочется всегда! =)

Решение, чертёж и ответ в конце книги.

Оставшиеся примеры параграфа посвящены не менее распространённому типу задач, где фигурируют неравенства.

Для начала разогревающий пример:

Задача 34
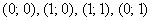
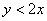
В квадрат с вершинами наудачу брошена точка . Найдите вероятность того, что координаты этой точки удовлетворяют неравенству.

Решение: изобразим на чертеже искомый квадрат и прямую :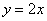

Общему множеству исходов соответствует площадь квадрата

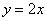
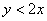
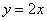
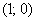
Прямая делит квадрат на треугольник и трапецию. Как определить фигуру, которая удовлетворяет условию ? Вспоминаем линейные неравенства: нужно взять любую точку, не принадлежащую прямой , например, точку и подставить её координаты в неравенство:

Получено верное неравенство, значит, множеству благоприятствующих исходов соответствует площадь 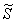трапеции. Рассчитаем данную площадь как сумму площадей прямоугольного треугольника и прямоугольника (разделены на чертеже пунктиром):

По геометрическому определению:
– вероятность того, что координаты брошенной в данный квадрат точки удовлетворяют неравенству.

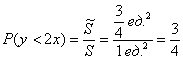
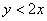
Ответ:

…аналитическую геометрию немного вспомнили, теперь на очереди математический анализ, ибо неравенства бывают не только линейными:

Задача 35
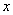
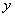
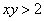
Загадываются два числа и в промежутке от 0 до 5. Какова вероятность, что ?

Схема решения уже знакома: коль скоро загадываются 2 произвольных числа от нуля до пяти (они могут быть и иррациональными), то общему количеству исходов соответствует площадь квадрата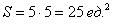
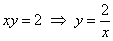
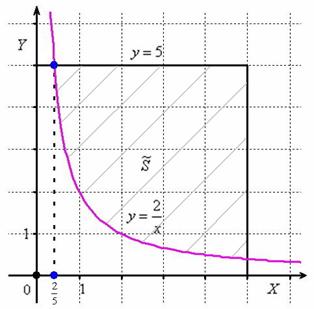
Изобразим ветвь гиперболы , которая делит квадрат на две части:

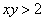
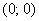
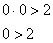
Теперь выясним, какой из этих двух «кусков» удовлетворяет неравенству . Для этого выберем любую точку, не принадлежащую гиперболе, проще всего взять , и подставим её координаты в наше неравенство:

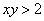
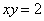
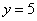
Получено неверное неравенство, а значит, условию соответствует «верхний кусок», площадь которого, деваться тут некуда, придётся вычислить с помощью определённого интеграла. Уточним нижний предел интегрирования аналитически (найдём точку пересечения гиперболы и прямой ):

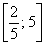
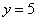
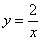
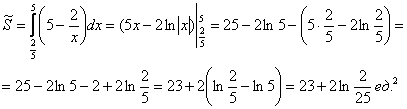
На отрезке прямая расположена не ниже гиперболы , по соответствующей формуле:

По геометрическому определению:
– вероятность того, что произведение двух загаданных в промежутке от 0 до 5 чисел окажется больше двух.

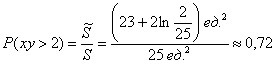
Ответ:

Аналогичный пример для самостоятельного решения:

Задача 36
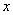
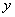
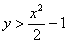
Загадываются два числа и в промежутке от 0 до 10. Какова вероятность, что ?
Данная задача (как, собственно, и предыдущая) допускает несколько способов расчёта площади, подумайте, какой путь более рационален.

В заключение следует отметить, что геометрическое определение вероятности тоже обладает своими недостатками. Один из них заключается в своеобразном парадоксе, давайте вспомним самый первый пример с отрезком 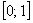, на который случайным образом падает точка. Возможно ли, что точка попадёт, например, на самый край отрезка? Да, такое событие возможно, но по геометрическому определению, его вероятность равна нулю! И то же самое можно сказать о любой точке отрезка! Дело в том, что с позиций геометрии размеры отдельно взятой точки равны нулю, и поэтому геометрическое определение вероятности здесь не срабатывает.

Полную и свежую версию этой книги в pdf-формате ,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Содержание

Решения задач на геометрическое определение вероятности
Решенные задач
Решебник по теории вероятности
Геометрическая вероятность
🎥 Видео

Видео:Геометрическая вероятность. С какой вероятностью можно составить треугольникСкачать

Решения задач на геометрическое определение вероятности

На этой странице вы найдете решения типовых задач по теории вероятностей на тему Геометрическое определение вероятности — задачи из методичек и популярных учебников.

Используйте их, чтобы научиться решать свои задачи (или заказывайте нам, если есть трудности). Краткую теорию по этой теме вы найдете в онлайн-учебнике.

Видео:Теория вероятностей | Математика TutorOnlineСкачать

Решенные задач

Задача 1. В прямоугольник 5*4 см 2 вписан круг радиуса 1,5 см. Какова вероятность того, что точка, случайным образом поставленная в прямоугольник, окажется внутри круга?

Задача 2. Какова вероятность Вашей встречи с другом, если вы договорились встретиться в определенном месте, с 12.00 до 13.00 часов и ждете друг друга в течение 5 минут?

Задача 3. На отрезок АВ длины L, брошена точка М так, что любое ее положение на отрезке равновозможно. Найти вероятность того, что меньший из отрезков (АМ или МВ) имеет длину, большую чем L/3.

Задача 4. Какова вероятность того, что сумма двух наугад взятых положительных чисел, каждое из которых не больше трех, не превзойдет трех, а их произведение будет не больше 2/7?

Задача 5. Наудачу взяты два положительных числа х и у, каждое из которых не превышает единицы. Найти вероятность того, что сумма х + у не превышает единицы, а произведение ху не меньше 0,09.

Задача 6. На отрезке АВ длиной l независимо одна от другой поставлены 2 точки L и M, положение каждой из которых равновозможно на AB. Найти вероятность того, что точка L будет ближе к точке M, чем к точке A.

Задача 7. Моменты начала двух событий наудачу распределены в промежутке времени от T1 до T2. Одно из событий длится 10 мин., другое – t мин. Определить вероятность того, что: а) события «перекрываются» по времени; б) «не перекрываются».
T1=1100; T2=1300; t=15.

Видео:Задача о встречеСкачать

Решебник по теории вероятности

Сложности с решением своей задачи? Возможно, она уже решена. Найди свою задачу в решебнике:

Видео:Геометрическая вероятность. Видеоурок по алгебре 11 классСкачать

Геометрическая вероятность

Цели и задачи: 1) Познакомить учащихся с одним из возможных способов задания

2) Повторение пройденного и закрепление навыков формализации

текстовых вероятностных задач с помощью геометрических фигур.

1) Знать определение геометрической вероятности выбора точки

внутри фигуры на плоскости и прямой;

2) Уметь решать простейшие задачи на геометрическую вероятность,

зная площади фигур или умея их вычислять.

I. Выбор точки из фигуры на плоскости.

Пример 1. Рассмотрим мысленный эксперимент: точку наудачу бросают на квадрат, сторона которого равна 1. Спрашивается, какова вероятность события, которое состоит в том, что расстояние от этой точки до ближайшей стороны квадрата не больше чем ?

В этой задаче речь идет о так называемой геометрической вероятности.

Рассмотрим более общие условия опыта.

Точку наудачу бросают в фигуру F на плоскости. Какова вероятность того, что точка попадает в некоторую фигуру G, которая содержится в фигуре F.

Ответ зависит от того, какой смысл мы вкладываем в выражение «бросить точку наудачу».

Обычно это выражение трактуют так:

1. Брошенная точка может попасть в любую часть фигуры F.

2. Вероятность того, что точка попадает в некоторую фигуру G внутри фигуры F, прямо пропорциональна площади фигуры G.

Подведем итог: пусть и — площади фигур F и G . Вероятность события А «точка Х принадлежит фигуре G, которая содержится в фигуре F», равна

Заметим, что площадь фигуры G не больше, чем площадь фигуры F, поэтому

Вернемся к нашей задаче. Фигура F в этом примере квадрат со стороной 1. Поэтому =1.

Точка удалена от границы квадрата не более чем на , если она попала в заштрихованную на рисунке фигуру G. Чтобы найти площадь , нужно из площади фигуры F вычесть площадь внутреннего квадрата со стороной .

Тогда вероятность того, что точка попала в фигуру G, равна

Пример 2. Из треугольника АВС случайным образом выбирается точка Х. Найти вероятность того, что она принадлежит треугольнику, вершинами которого являются середины сторон треугольника.

Решение: Средние линии треугольника разбивают его на 4 равных треугольников. Значит,

Вероятность того, что точка Х принадлежит треугольнику KMN, равна:

Вывод. Вероятность попадания точки в некоторую фигуру прямо пропорциональна площади этой фигуры.

Задача. Нетерпеливые дуэлянты.

Дуэли в городе Осторожности редко кончаются печальным исходом. Дело в том, что каждый дуэлянт прибывает на место встречи в случайный момент времени между 5 и 6 часами утра и, прождав соперника 5 минут, удаляется. В случае же прибытия последнего в эти 5 минут дуэль состоится. Какая часть дуэлей действительно заканчивается поединком?

Решение: Пусть х и у обозначают время прибытия 1-го т 2-го дуэлянтов соответственно, измеренное в долях часа начиная с 5 часов.