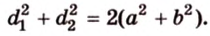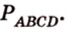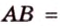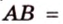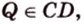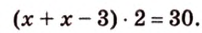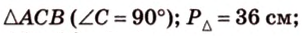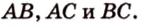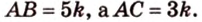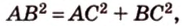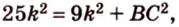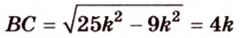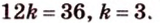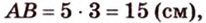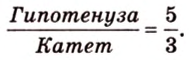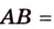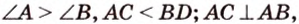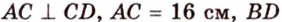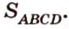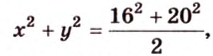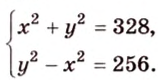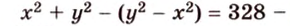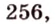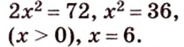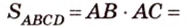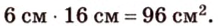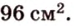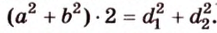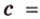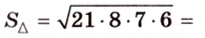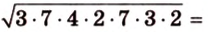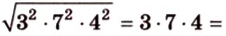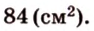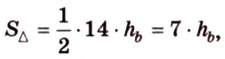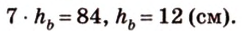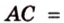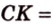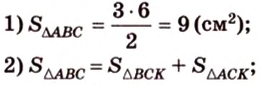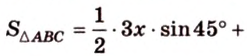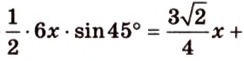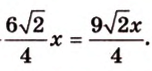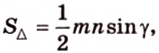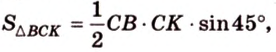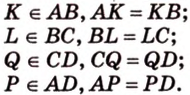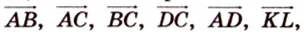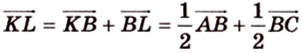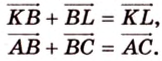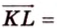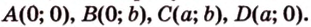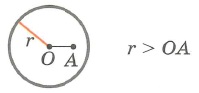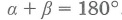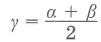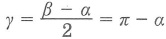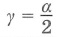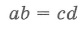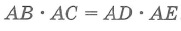- Взаимное расположение прямой и окружности
- Отрезки и прямые, связанные с окружностью. Теорема о бабочке
- Отрезки и прямые, связанные с окружностью
- Свойства хорд и дуг окружности
- Теоремы о длинах хорд, касательных и секущих
- Доказательства теорем о длинах хорд, касательных и секущих
- Теорема о бабочке
- Please wait.
- We are checking your browser. mathvox.ru
- Why do I have to complete a CAPTCHA?
- What can I do to prevent this in the future?
- Планиметрия — формулы, определение и вычисление с примерами решения
- Что такое планиметрия
- Аксиомы планиметрии
- Опорные факты курса планиметрии
- Взаимное расположение прямых на плоскости
- Окружность и круг
- Многоугольники
- Треугольник и его элементы
- Выпуклые четырехугольники
- Задачи и методы их решения
- Что такое математическая задача?
- Пример №1
- Пример №2
- Пример №3
- Алгебраический метод решения задач
- Пример №4
- Пример №5
- Метод площадей
- Пример №6
- Пример №7
- Метод векторов
- Пример №8
- Метод координат
- Пример №9
- Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности
- Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности.
- Прямые, отрезки и углы, связанные с окружностью:
- Взаимное расположение окружности и прямой:
- Взаимное расположение окружности и точки:
- Взаимное расположение двух окружностей:
- Свойства углов, связанных с окружностью:
- Метрические соотношения в окружности (длины отрезков):
- 📸 Видео
Видео:Взаимное расположение окружности и прямой. 7 класс.Скачать

Взаимное расположение прямой и окружности
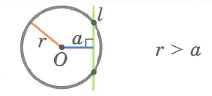
Выясним количество общих точек прямой и окружности в зависимости от их взаимного расположения. Если прямая l проходит через центр O окружности (Рис.1), то она пересекает окружность в двух точках, которые являются концами диаметра окружности.
Пусть прямая не проходит через центр окружности. Проведем перпендикуляр OH к прямой l (Рис.2, Рис.3, Рис.4). Обозначим расстояние от центра окружности до прямой l буквой d. Рассмотрим сколько общих точек будут иметь прямая и окружность в зависимости от соотношения d и r.
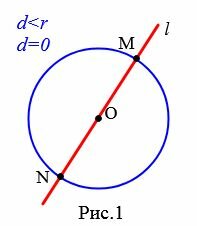 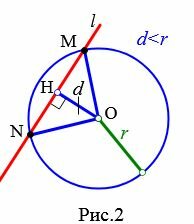 |
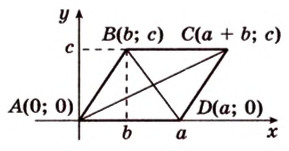
Теорема 1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
В этом случае прямая называется секущей по отношению к окружности.
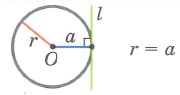
Доказательство. Пусть расстояние от центра окружности до прямой меньше радиуса окружности: d Теорема 2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.
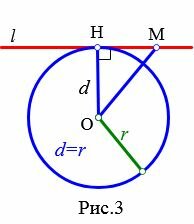 |
Доказательство. Пусть расстояние от центра окружности до прямой равно радиусу окружности: d=r (Рис.3). В этом случае OH=r, т.е. точка H лежит на окружности и является общей точкой прямой l и окружности. Возьмем на прямой l любую точку M отличной от H. Тогда расстояние от OM больше расстояния OH=r, поскольку наклонная OM больше перпендикуляра OH к прямой l. Следовательно точка M не лежит на окружности. Получили, что точка H единственная общая точка прямой l и окружности.
Теорема 3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.
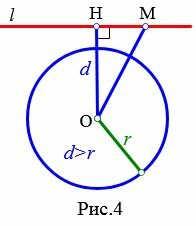 |
Доказательство. Пусть расстояние от центра окружности до прямой больше радиуса окружности:d>r (Рис.4). Тогда ( small OH > r). Возьмем на прямой l любую точку M отличной от H. Тогда ( small OM > OH>r). Следовательно точка M не лежит на окружности. Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.
Видео:Урок по геометрии ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИСкачать

Отрезки и прямые, связанные с окружностью. Теорема о бабочке
 Отрезки и прямые, связанные с окружностью Отрезки и прямые, связанные с окружностью |
 Свойства хорд и дуг окружности Свойства хорд и дуг окружности |
 Теоремы о длинах хорд, касательных и секущих Теоремы о длинах хорд, касательных и секущих |
 Доказательства теорем о длинах хорд, касательных и секущих Доказательства теорем о длинах хорд, касательных и секущих |
 Теорема о бабочке Теорема о бабочке |
Видео:8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства |
| Окружность |  |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
Видео:Взаимное расположение прямой и окружности, математика 6 классСкачать

Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  | Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  | У равных дуг равны и хорды. |
| Параллельные хорды |  | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
 |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Большая из двух хорд расположена ближе к центру окружности.

У равных дуг равны и хорды.

Дуги, заключённые между параллельными хордами, равны.
Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема |
| Пересекающиеся хорды |  |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.


| Пересекающиеся хорды | |||||
 | |||||
| Касательные, проведённые к окружности из одной точки | |||||
 | |||||
| Касательная и секущая, проведённые к окружности из одной точки | |||||
 | |||||
| Секущие, проведённые из одной точки вне круга | |||||
 | |||||
| Пересекающиеся хорды |
 |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Видео:Взаимное расположение прямой и окружности. 6 классСкачать

Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Видео:Взаимное расположение окружностей. 7 класс.Скачать

Теорема о бабочке
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
Видео:70. Взаимное расположение прямой и окружностиСкачать

Please wait.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

We are checking your browser. mathvox.ru
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:Лекция Взаимное расположение прямой и окружностиСкачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6cfbf3665f20164e • Your IP : 85.95.179.65 • Performance & security by Cloudflare
Видео:Окружность и круг, 6 классСкачать

Планиметрия — формулы, определение и вычисление с примерами решения
Содержание:
В окружающем нас мире существует много разнообразных предметов, каждый из которых обладает определенным набором характеристик: размеры, форма, цвет, твердость, химический состав и т.д. Например, круг радиуса 10 см можно вырезать из металлического листа или из бумаги. Понятно, что эти предметы будут иметь как одинаковые характерные свойства, так и различные. Что касается формы и количественных характеристик, то они являются одинаковыми фигурами — два круга радиуса 10 см. Школьные дисциплины, изучающие пространственную форму и количественные характеристики предметов и явлений материального мира, — алгебра и геометрия -относятся к математическим.
Геометрия — это наука о пространственной форме и количественных характеристиках предметов реального мира.
Исследованием прочих характеристик предметов окружающей среды занимаются другие дисциплины. Если в процессе изучения предмета не учитывать никаких других его характеристик, кроме пространственной формы и размеров, получим абстрактный объект, который называют геометрической фигурой.
Слово «геометрия» — греческого происхождения и в переводе означает землеизмерение. Геометрия, которую изучают в школе, называется евклидовой по имени древнегреческого ученого Евклида (см. рубрику «Из летописи геометрии» на с. 45). Школьная геометрия состоит из двух частей: планиметрии и стереометрии. С планиметрией вы ознакомились в основной школе, а стереометрию будете изучать в старших классах.
Видео:Взаимное расположение прямой и окружностиСкачать

Что такое планиметрия
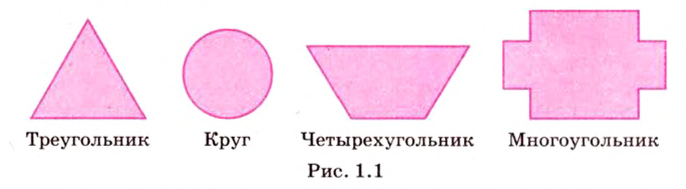
Планиметрия — это раздел геометрии, который изучает геометрические фигуры на плоскости (рис. 1.1).
Стереометрия — это раздел геометрии, который изучает фигуры в пространстве.
Геометрические фигуры — это абстрактные фигуры, которые напоминают окружающие предметы. Чтобы отличить одну геометрическую фигуру (или понятие) от другой, их описывают в виде утверждения, которое называют определением.
Определение — это утверждение, которое описывает существенные свойства предмета (понятия), позволяющие отличить его от других. Как выяснилось, определить все геометрические фигуры невозможно. Например, точка, прямая, плоскость. Их называют неопределяемыми, начальными (с которых все начинается), или, как принято в планиметрии, основными.
Логическое построение планиметрии можно описать как последовательность следующих этапов.
- Выбор геометрических понятий, которые называют основными (абстрактных фигур).
- Формулирование основных свойств для этих геометрических понятий с помощью утверждений, которые считаются истинными без доказательств.
- Построение других понятий, определяемых через основные понятия и их свойства, и утверждений, истинность которых устанавливается путем доказательств, опираясь на известные.
Такое построение науки называют аксиоматическим (греч. «аксиома», что в переводе означает уважение, авторитет, неопровержимая истина). Аксиома — это утверждение, принимающееся как истинное без доказательств. Основные свойства простейших геометрических фигур, которые считаются истинными без доказательства и являются исходными при доказательстве других свойств, называют аксиомами геометрии.
Для школьного курса планиметрии определены:
- Основные геометрические фигуры (понятия) — точка, прямая. (Точка — простейшая геометрическая фигура. Все другие геометрические фигуры состоят из точек, в том числе и прямая.)
- Аксиомы планиметрии — это основные свойства простейших геометрических фигур.
- Система определений планиметрических фигур и теорем, выражающих их свойства.
К определяемым понятиям в геометрии относят отрезок, луч, треугольник и т. п., поскольку для них существуют объяснения «что это такое?». Определяемых понятий много. Приведем пример.
Пусть на прямой а заданы две различные точки Аи В. Фигуру, состоящую из всех точек прямой а, которые лежат между точками А и В, включая точки А и В, называют отрезком (рис. 1.2). Точки А и В называются концами отрезка, а все другие точки — внутренними точками отрезка. Таким образом, отрезок — определяемое понятие.
Аксиомы планиметрии
С целью установления правильности утверждения о свойствах той или иной геометрической фигуры прибегают к некоторым рассуждениям. Среди них есть такие, которые требуют доказательства (теоремы, задачи). Утверждение, истинность которого устанавливается путем доказательства и которое используется для доказательства других утверждений, называют теоремой.
Теорема состоит из: условия и вывода. Для доказательства теорем в школьном курсе геометрии в основном используют следующие методы:
- а) по структуре доказательства — прямой (аналитический и синтетический), от противного;
- б) по использованию математического аппарата — алгебраический, координатный, векторный и др.
Все рассуждения при доказательстве теорем произвольным методом основываются на аксиомах и известных доказанных фактах. Т.е. чтобы доказать теорему, разрешается пользоваться только основными свойствами простейших фигур (аксиомами) и свойствами, доказанными ранее (теоремами). Никакими другими свойствами фигур, даже если они представляются очевидными, пользоваться нельзя. Например, доказывая теоремы, можно использовать рисунки. Однако это лишь геометрическая модель содержания текста, выраженного словами, поэтому делать по рисунку выводы о свойствах фигур не разрешается.
Итак, геометрия, как и другие математические науки, строится по такой схеме: сначала следует ввести основные понятия, задать аксиомы (правила игры), а потом, опираясь на аксиомы, выводить другие факты (проводить игру по определенным правилам, не противоречащим друг другу).
Опорные факты курса планиметрии
Данный параграф предназначен для повторения курса планиметрии. Необходимость в нем обусловлена тем, что многие вопросы планиметрии на первом этапе обучения в школе рассматриваются несколько поверхностно. В следующих классах уровень изучения материала повышается, а вернуться и углубить пройденное удается не всегда. Поэтому мы систематизируем и обобщим основные сведения по планиметрии, условно разбив их на блоки: взаимное расположение прямых на плоскости; окружность и круг; многоугольники; треугольник и его элементы; выпуклые четырехугольники.
Взаимное расположение прямых на плоскости
Две прямые на плоскости могут пересекаться только в одной точке или не пересекаться, т.е. быть параллельными. При пересечении двух прямых образуются смежные и вертикальные углы. Смежные углы дополняют друг друга до 180°, а вертикальные — равны. Меньший из них называется углом между прямыми. На рисунке 1.3 изображены две прямые 
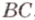
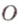
и
,
и
— вертикальные;
и
,
и
,
и
,
и
— смежные.
Если один из углов при пересечении двух прямых равен 90°, то все другие углы — смежные и вертикальные — также равны 90°. Такие прямые называют взаимно перпендикулярными. Записывают, например, 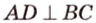
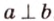
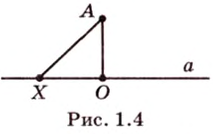
Расстоянием от точки 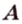
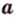
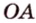
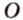
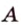
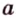
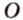
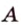
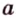
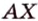
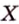
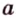
Две различные прямые 
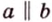
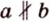
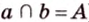
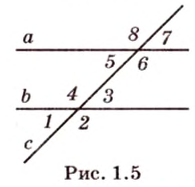
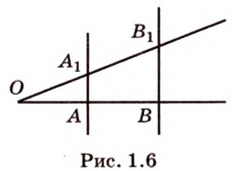
Вследствие пересечения двух прямых третьей прямой образуется восемь углов (рис. 1.5) (прямые а и Ь могут пересекаться, но прямая с через точку их пересечения не проходит):
- внутренние односторонние (углы 4 и 5, 3 и 6);
- внутренние разносторонние (углы 3 и 5, 4 и 6);
- внешние односторонние (углы 1 и 8, 2 и 7);
- внешние разносторонние (углы 1 и 7, 2 и 8);
- соответствующие (углы 1 и 5, 2 и 6, 8
Признаки параллельности прямых:
- Если при пересечении двух прямых
и
третьей прямой внутренние (или внешние) разносторонние углы равны или внутренние односторонние в сумме составляют 180°, то
и
параллельны.
- Две прямые, параллельные третьей, параллельны между собой.
Окружность и круг
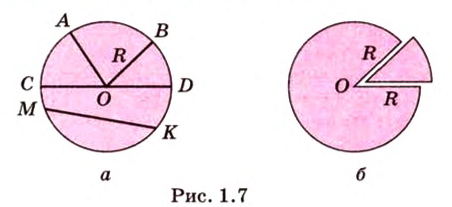
Кругом с центром 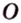
Отрезки, которые соединяют центр с точками окружности и имеют длину 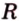
Части круга, на которые он делится двумя радиусами, называют круговыми секторами (рис. 1.7, б).
Хорда — отрезок, который соединяет две точки окружности 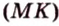
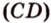
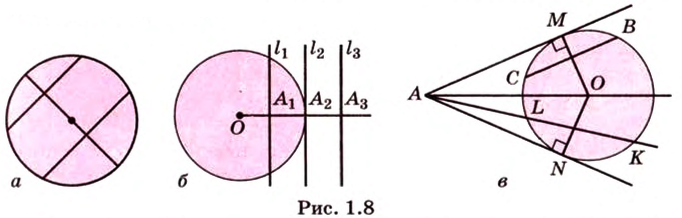
Через три точки, не лежащие на одной прямой, проходит единственная окружность. Диаметр, перпендикулярный к хорде, делит пополам эту хорду и обе дуги, которые стягиваются ею, и наоборот, если диаметр проведен через середину хорды, то он перпендикулярен этой хорде и делит пополам дугу, которую она стягивает (рис. 1.8, а).
Дуги, которые находятся между параллельными хордами, равны между собой. Равные дуги стягиваются равными хордами, и наоборот, равные хорды стягивают равные дуги.
Равные хорды одинаково отдалены от центра, и наоборот, хорды, одинаково отдаленные от центра, равны между собой. Большая из двух хорд меньше отдалена от центра, и наоборот, из двух хорд больше та, которая меньше отдалена от центра (рис. 1.8, а).
Каким может быть взаимное расположение прямой и окружности?
Рассмотрим окружность с центром 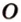
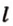
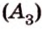
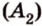
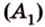
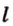
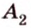
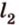
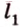
Прямая, проходящая через точку окружности, является касательной к окружности только тогда, когда она перпендикулярна радиусу, проведенному в эту точку. Если касательная параллельна хорде окружности, то точка касания делит пополам дугу, которую стягивает хорда (рис. 1.8, в; 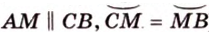
Если из одной точки к окружности проведены две касательные, то отрезки этих касательных (от точек касания до данной точки) равны между собой, а луч, проведенный через данную точку и центр окружности, делит пополам угол между касательными (рис. 1.8, в; 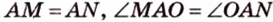
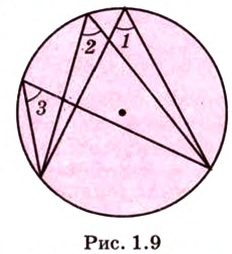
Вписанным углом в окружность называют угол, образованный двумя хордами, выходящими из одной точки на окружности (рис. 1.9). Вписанный угол измеряется половиной дуги, на которую он опирается. Вписанные углы, опирающиеся на одну дугу, между собой равны. Вписанный угол, который опирается на полуокружность (на диаметр), — прямой.
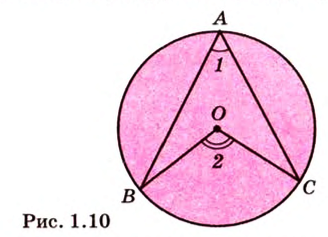
Угол с вершиной в центре окружности называется центральным углом. Центральный угол, стороны которого пересекают окружность в тех же точках, что и вписанный, называется соответствующим центральным углом вписанного (рис. 1.10). Мера вписанного угла равна половине меры соответствующего центрального или дополняет его половину до 180°. Угол, образованный хордой и касательной, которая проходит через конец хорды, измеряется половиной дуги, находящейся между сторонами этого угла (рис. 1.11; 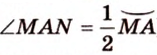
Угол, образованный двумя касательными, называется описанным (рис. 1.8, в; 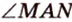
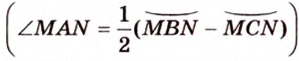
Длину окружности находят по формуле: 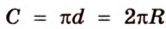
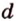
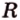
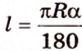
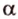
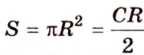
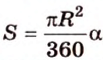
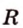
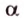
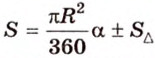
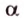
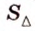
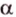
Многоугольники
Многоугольником называется простая замкнутая ломанная. Например, многоугольником 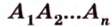
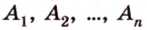
Плоский многоугольник — часть плоскости, ограниченная многоугольником.
Многоугольник может быть выпуклым или невыпуклым.
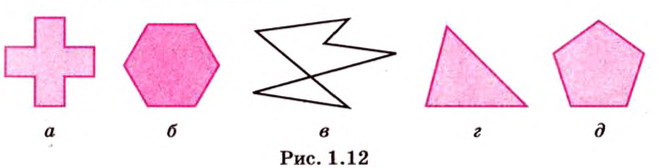
Многоугольник выпуклый, если он лежит в одной полуплоскости относительно каждой прямой, проходящей через две его соседние вершины (рис. 1.12, б, г, д).
Многоугольники называют равными, если при наложении они совмещаются. Для выпуклого 
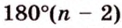

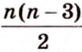

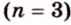
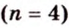
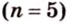
Как построить правильный 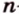
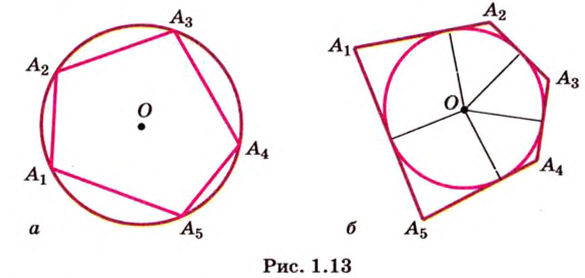
Если окружность разделить на 

Если окружность разделить на 

Вокруг каждого правильного многоугольника можно описать окружность или в каждый правильный многоугольник можно вписать окружность.
В правильном многоугольнике центры описанной и вписанной окружностей совпадают. Общий центр описанной и вписанной окружностей называется центром правильного многоугольника. Радиус вписанной окружности называют апофемой правильного многоугольника.
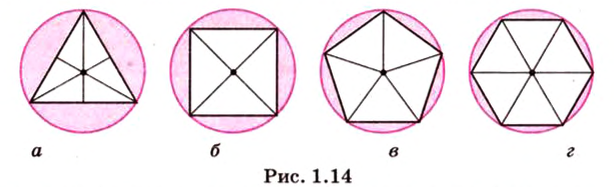
Угол, образованный двумя радиусами, проведенными через смежные вершины правильного многоугольника, называется его центральным углом. Все центральные углы правильного многоугольника равны между собой и составляют 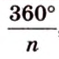

В правильном 

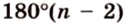
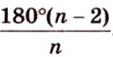
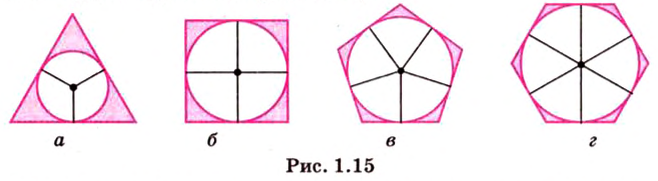
Окружность, вписанная в правильный многоугольник, касается его сторон в их серединах. Центр окружности, вписанной в правильный многоугольник, является точкой пересечения серединных перпендикуляров его сторон (рис. 1.15).
Если сторона правильного многоугольника равна 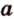
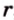
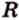
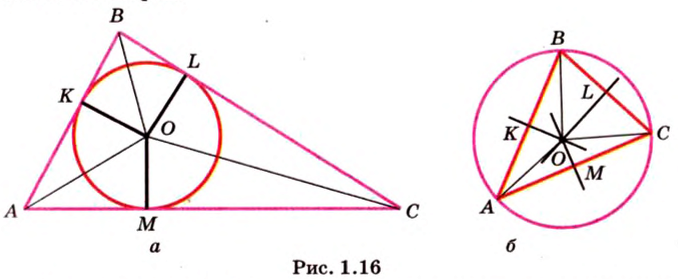
Простейшим многоугольником является треугольник. В любой треугольник можно вписать окружность, причем только одну. На рисунке 1.16, 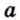

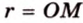
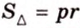
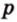
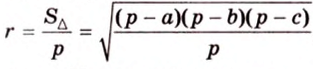
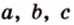
Можно ли в любой четырехугольник вписать окружность?
Ответ. Нельзя. В четырехугольник можно вписать окружность только при условии, что суммы длин его противоположных сторон равны.
Вокруг произвольного треугольника можно описать окружность, притом только одну (см. рис. 1.16, б). Центр окружности, описанной вокруг треугольника, является точкой пересечения серединных перпендикуляров, проведенных к его сторонам. Центр окружности 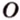
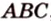
На рисунке 1.16, б изображена окружность с центром 
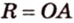
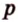
Можно ли описать окружность вокруг произвольного четырехугольника?
Ответ. Нельзя. Вокруг четырехугольника можно описать окружность только тогда, когда суммы противоположных углов равны 180°.
Треугольник и его элементы
Треугольником называется фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, которые попарно соединяют эти точки. Рассмотрим 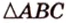
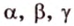
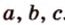
Треугольник называется тупоугольным, прямоугольным или остроугольным, если его наибольший внутренний угол соответственно больше, равен или меньше 90°.
Треугольник называется равнобедренным, если у него две стороны равны (боковые стороны). Основанием равнобедренного треугольника является сторона, которая не равна ни одной из двух других равных сторон.
Треугольник, все стороны которого равны, называется равносторонним, или правильным.
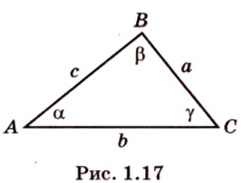
Соотношение между сторонами и углами треугольника:
- — против большей стороны лежит больший угол, и наоборот;
- — против равных сторон лежат равные углы;
- — теорема синусов:
;
- — теорема косинусов:
(квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними).
Треугольник можно определить любой тройкой таких основных элементов: либо двумя сторонами и углом между ними, либо одной стороной и двумя углами, либо тремя сторонами.
Например, 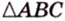
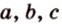
;
Соотношение между внутренними и внешними углами треугольника: любой внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Из трех отрезков можно образовать треугольник тогда и только тогда, когда любая его сторона меньше суммы и больше разности двух других его сторон. В любом треугольнике можно провести три медианы, три биссектрисы и три высоты.
Свойства биссектрисы угла треугольника: биссектрисы треугольника пересекаются в одной точке, которая лежит в середине треугольника и является центром вписанной
в него окружности.
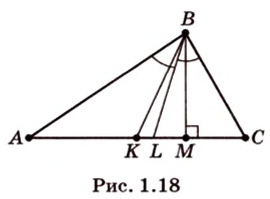
Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим к ней сторонам (рис. 1.18; 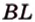
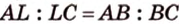
Основные свойства медиан треугольника:
- Медианы треугольника пересекаются в одной точке, которая лежит в середине треугольника.
- Медианы треугольника точкой их пересечения делятся в соотношении 2 : 1 (считая от вершин треугольника).
- Медиана делит треугольник на два треугольника, площади которых равны (рис. 1.18;
— медиана,
).
- Три медианы треугольника делят треугольник на шесть треугольников, площади которых равны.
Прямые, на которых лежат высоты треугольника, пересекаются в одной точке — ортоцентре треугольника, которая может находиться во внутренней или внешней области треугольника. Высоты треугольника, проведенные к его сторонам 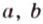
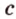
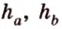
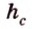
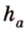
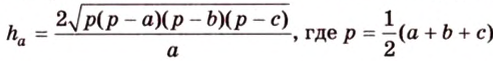
Медиана треугольника 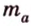
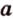
В каждом треугольнике можно построить три средние линии — отрезки, соединяющие середины двух его сторон. Средняя линия треугольника параллельна третьей стороне треугольника и равна ее половине. Средняя линия треугольника отсекает от него подобный треугольник, площадь которого относится к площади основного треугольника как 1 : 4.
Свойства равнобедренного треугольника: углы при основании треугольника равны; высота, проведенная к основанию, является также биссектрисой и медианой.
Свойства равностороннего треугольника: все углы равны (каждый угол равен 60°); каждая из трех высот является также биссектрисой и медианой; центр окружности, описанной вокруг треугольника, совпадает с центром окружности, вписанной в него.
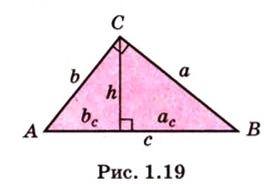
Прямоугольный треугольник имеет сторону, которая лежит против прямого угла, — гипотенузу 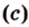
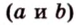
Стороны прямоугольного треугольника 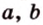
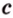
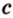
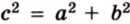
длины гипотенузы равен сумме квадратов длин катетов.
Свойства прямоугольного треугольника:
- Катет является средним пропорциональным между гипотенузой и проекцией этого катета на гипотенузу:
и
(рис. 1.19).
- Высота, проведенная из вершины прямого угла, является средним пропорциональным между проекциями катетов на гипотенузу:
.
- Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы.
- Для сторон прямоугольного треугольника справедливы отношения:
Выпуклые четырехугольники
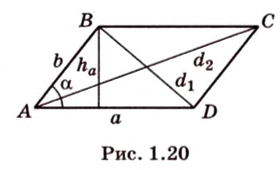
Четырехугольник, противоположные стороны которого попарно параллельны, называется параллелограммом (рис. 1.20).
- Середина диагонали параллелограмма является его центром симметрии.
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.
- Каждая диагональ параллелограмма делит его на два равных треугольника.
- Диагонали параллелограмма делятся точкой пересечения пополам.
- Сумма квадратов диагоналей параллелограмма (
и
) равна сумме квадратов всех его сторон:
Чтобы доказать, что некоторый заданный четырехугольник является параллелограммом, следует, согласно определению, убедиться в параллельности его противоположных сторон. Иногда такие рассуждения являются громоздкими, а иногда -излишними. Существуют другие доказанные признаки, на основании которых можно утверждать, что данный четырехугольник является действительно параллелограммом.
Если в четырехугольнике исполняется любое из таких условий:
- противоположные стороны попарно равны;
- две противоположные стороны равны и параллельны;
- противоположные углы попарно равны;
- диагонали в точке пересечения делятся пополам, — то такой четырехугольник является параллелограммом.
Прямоугольник — это параллелограмм, в котором все углы равны. Поскольку сумма углов четырехугольника равна 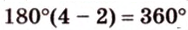
Для прямоугольника справедлива и обратная теорема: если у параллелограмма диагонали равны, то он — прямоугольник. Эта теорема является признаком прямоугольника.
Ромб — это параллелограмм, в котором все стороны равны. Кроме общих свойств параллелограмма, ромб имеет и другие, характерные только для него.
Диагонали ромба взаимно перпендикулярны и делят его углы пополам. Справедлива и обратная теорема, которая является признаком ромба: если у параллелограмма диагонали взаимно перпендикулярны или если в нем диагонали делят углы пополам, то такой параллелограмм — ромб.
Квадрат — это параллелограмм, в котором все углы равны и все стороны равны.
Таким образом, квадрат — это прямоугольник с равными сторонами или квадрат — это ромб с равными углами (прямыми). Очевидно, что квадрат имеет все свойства прямоугольника и ромба.
Трапеция — это четырехугольник, в котором только две противоположные стороны параллельны. Эти параллельные стороны называются основаниями трапеции, две другие стороны — боковыми сторонами.
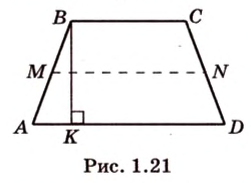
Если боковые стороны трапеции равны между собой, такую трапецию называют равнобокой (рис. 1.21; 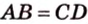
Равнобокая трапеция имеет такие свойства:
- Углы, прилежащие к основанию равнобокой трапеции, равны. Справедливо и обратное утверждение: если углы, прилежащие к основанию трапеции, равны, то такая трапеция равнобокая.
- Диагонали равнобокой трапеции равны.
- Сумма противоположных углов равнобокой трапеции равна 180°.
Отрезок, соединяющий середины боковых сторон трапеции, называется ее средней линией (рис. 1.21; 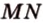
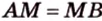
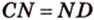
Средняя линия трапеции параллельна ее основаниям и равна их полусумме (рис. 1.21; 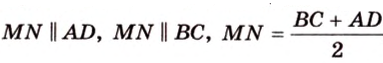
Видео:Взаимное расположение прямой и окружностиСкачать

Задачи и методы их решения
Для геометрии закономерным является то, что введенные основные понятия и сформулированная аксиоматика составляют основу для новых утверждений. Однако справедливость последних необходимо доказывать путем определенных рассуждений, основывающихся на ранее доказанных утверждениях или аксиомах. Так формируются математические задачи.
Что такое математическая задача?
Существуют разные определения этого понятия, например: математическая задача — это любое требование вычислить, построить, доказать, исследовать что-либо, или вопрос, равносильный такому требованию.
В каждой задаче что-то дано (условие) и что-то нужно доказать или найти (требование, вывод). Выполнить поставленное требование — и означает решить задачу. Отметим, что если истинность какого-либо, часто используемого математического утверждения установлена путем рассуждения (доказательства), то такое утверждение называют теоремой.
Можно ли утверждать, что для успешного решения геометрических задач и доказательства теорем достаточно свободно владеть всем теоретическим материалом?
Нет. Это не так. При хорошем знании теории следует овладеть еще и практическими навыками. А это возможно только в процессе решения задач, начиная с простейших и постепенно переходя к более сложным.
Математические задачи условно разделены на четыре вида, в соответствии с их требованиями: задачи на вычисление, доказательство, исследование и построение. С ними вы уже ознакомились в курсе планиметрии.
Приступая к решению задачи, следует выбрать метод. Методы делят:
- а) по структуре — синтетический, аналитический, от противного и др.;
- б) по использованию математического аппарата — алгебраический, векторный, координатный, метод площадей, метод геометрических преобразований и др.
Суть синтетического метода заключается в том, что, исходя из условия задачи или теоремы с использованием известных утверждений строится цепочка логических рассуждений, последнее из которых совпадает с требованием задачи. Приведем пример.
Пример №1
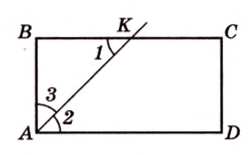
Биссектриса угла прямоугольника делит большую сторону на два отрезка -7 см и 9 см. Найдите периметр этого прямоугольника.
Дано: 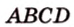
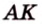

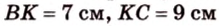
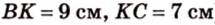
Найти:
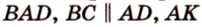
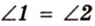
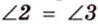
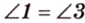
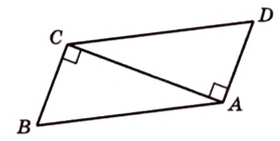
В 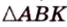
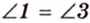
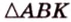
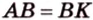
1. Если 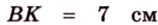
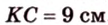
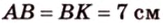
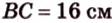
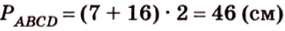
2. Если 
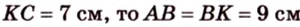
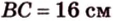
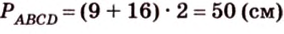
Ответ. 46 см или 50 см.
Почему именно так?
Пусть по условию 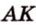
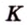
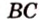
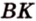
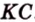
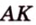
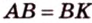
Если 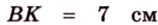
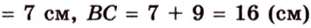
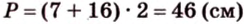
Если 
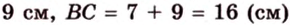
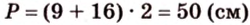
Эта задача является опорной, поскольку на такой идее строятся многие задачи и для параллелограмма, и для трапеции. У этих фигур биссектриса угла отсекает всегда равнобедренный треугольник.
Отметим, что сокращенное обозначение углов в виде 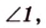
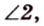
Как видим, в процессе решения задачи 1 используются только известные геометрические утверждения и производятся соответствующие вычисления. Причем для каждой геометрической задачи такие рассуждения свои.
Суть аналитического метода состоит в том, что, исходя из требования (вывода) утверждения (теоремы или задачи) и опираясь на известное утверждение, строится цепочка логических рассуждений, которая показывает, что требование является следствием условия. Приведем пример.
Пример №2
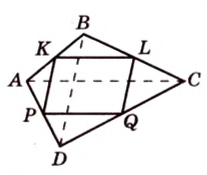
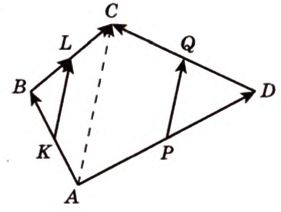
Докажите, что середины сторон любого выпуклого четырехугольника являются вершинами параллелограмма.
Дано: 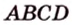

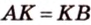
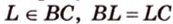

Доказать: 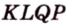
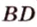
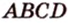
В 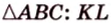
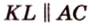
В 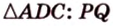

Имеем: 1. 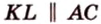
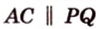
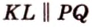
2. Аналогично 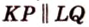
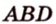
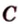
Итак, в четырехугольнике 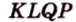
Почему именно так?
Требование задачи: доказать. Это означает, что истинность утверждения следует подтвердить цепочкой рассуждений.
Чтобы четырехугольник 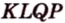
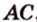
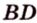
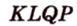
Отметим: доказательство того, что четырехугольник, вершины которого являются серединами произвольного выпуклого четырехугольника, — параллелограмм, можно проводить и другими методами.
Синтетический и аналитический методы называют также прямыми методами решения математических задач.
Чтобы решить задачу прямым методом, следует начать с анализа содержания задачи, от которого зависит выбор метода решения. Далее необходимо создать модель в виде рисунка и продолжить рассуждать над каждым действием, которые в совокупности образуют цепочку действий, ведущих либо от условия к требованию, либо от требования к условию.
Суть метода доказательства от противного состоит в том, что, имея утверждение, строим новое, возразив выводу данного. Формулируется утверждение. Исходя из вывода противоположного утверждения, строим цепочку истинных утверждений, пока не получим утверждение, которое противоречит либо условию, либо известной аксиоме или теореме, либо предположению. Таким образом приходим к выводу, что противоположное утверждение ошибочно, а потому исходное является истинным (тут действует логический закон: из двух противоположных утверждений одно истинное, другое ошибочное, третьего не дано). Рассмотрим пример.
Пример №3
Докажите утверждение: если две прямые параллельны третьей, то они параллельны между собой.
Строим противоположное утверждение: существуют две прямые, параллельные третьей и не параллельные между собой.
От противного. Предположим, что 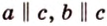
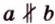
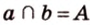
Получили утверждение, которое противоречит аксиоме параллельности: через точку 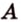
Почему именно так?
Исходим из вывода нового утверждения: пусть прямые 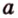
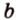
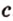
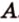
Математическую задачу считают решенной, если:
- записан ответ в виде числа, выражения, указан алгоритм построения рисунка, если это задача на вычисление, построение или исследование;
- подтверждено сформулированное в задаче утверждение, если это задача на доказательство.
Метод от противного называют непрямым методом решения математических задач.
Рассмотрим некоторые другие методы решения геометрических задач, которые делят на виды по использованию математического аппарата.
Алгебраический метод решения задач
Решая задачу алгебраическим методом, следует уделить внимание таким этапам:
- Моделирование текста задачи с помощью рисунка (в большинстве случаев).
- Введение обозначений искомых величин или тех, которые приводят к искомым (чаще всего буквами латинского алфавита).
- Составление уравнения или системы уравнений с использованием введенных определений и известных геометрических соотношений между искомыми и данными величинами.
- Решение составленного уравнения или системы уравнений. Возврат к введенным обозначениям и определение искомых геометрических величин. По необходимости, выполнение исследования найденных решений.
- Запись ответа.
Задачи, в которых задана зависимость между двумя измерениями, сводятся к решению уравнения. Например, одна из сторон параллелограмма на 3 см длиннее другой, а периметр -30 см. Нужно найти длины сторон параллелограмма. Тогда, введя переменную 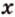
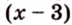
Приведем другие примеры решения задач алгебраическим методом.
Пример №4
Периметр прямоугольного треугольника равен 36 см. Гипотенуза относится к катету как 5 : 3. Найдите стороны треугольника.
Дано: 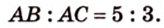
Найти:
Обозначим коэффициент пропорциональности через 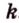
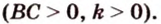
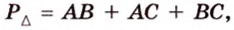
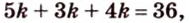
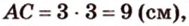
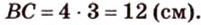
Ответ. 15 см, 9 см и 12 см.
Почему именно так?
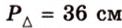
Пусть 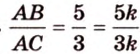
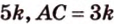
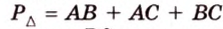
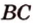
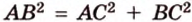
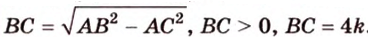
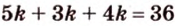
Пример №5
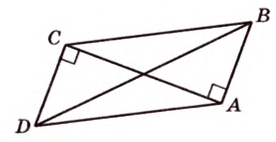
В параллелограмме диагонали равны 16 см и 20 см. Меньшая из них перпендикулярна к его стороне. Найдите площадь этого параллелограмма.
Дано: 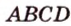
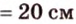
Найти:
Почему именно так?
Пусть 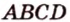
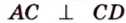
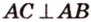
Обозначим стороны параллелограмма: 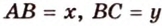
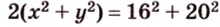
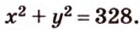
По теореме Пифагора из 
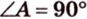
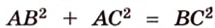
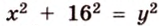
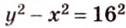
Составим систему уравнений:
Ответ.
Почему именно так?
В ходе решения этой задачи сначала выбираем формулу для вычисления площади параллелограмма. 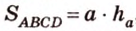
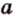
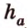
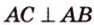
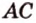
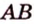
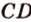
Длины сторон параллелограмма являются неизвестными, поэтому, очевидно, следует составить систему уравнений. Одно уравнение можно получить по вышеуказанной формуле, а второе — исходя из того, что диагональ параллелограмма перпендикулярна, имеем прямоугольный треугольник с двумя неизвестными сторонами (они же и стороны параллелограмма).
Отметим, что, принимая во внимание требование задачи, можно не искать обе стороны параллелограмма, а только, например, сторону 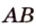
Метод площадей
Если условие задачи содержит данные, по которым легко найти площадь одним из способов, то это делают в первую очередь. С помощью другого способа для вычисления площади этой самой фигуры делают второй шаг — составляют уравнение, в котором одно из линейных измерений неизвестно. Приравнивая площади, получают уравнение с одним неизвестным.
Пример №6
Стороны треугольника равны 13 см, 14 см и 15 см. Вычислите высоту, проведенную к стороне, которая имеет длину 14 см.
Пусть 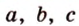
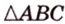
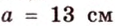
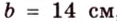
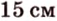
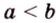
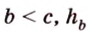
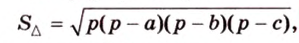
Ответ. 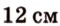
Почему именно так?
Имея три стороны треугольника 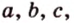
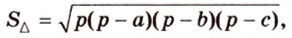
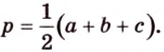
С другой стороны, площадь треугольника можно найти по формулам: 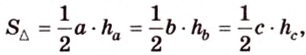
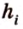

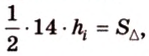
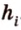
Отметим, что хотя во время решения задачи 6 использовалось алгебраическое уравнение, более существенными в решении этой задачи являются рассуждения о площади фигуры. Поэтому такой метод получил название метод площадей.
Пример №7
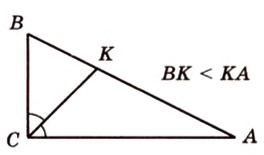
Катеты прямоугольного треугольника равны 3 см и 6 см. Найдите длину биссектрисы прямого угла.
Дано: 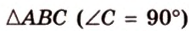
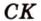
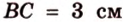
Найти: 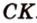
Пусть 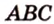
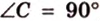
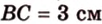
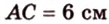
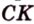
Введем обозначение: 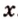
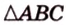
Почему именно так?
Площадь 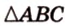
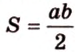
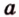
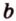
Биссектриса разделила 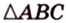
где 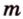
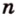
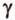
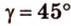
Поскольку 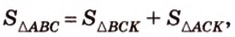
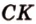
Метод векторов
Чтобы применить метод векторов к решению задачи, необходимо выполнить следующие действия:
- Перевести задачу на язык векторов, т.е. рассмотреть некоторые данные в ней отрезки как векторы и составить векторное равенство.
- Осуществить преобразование для векторного равенства, пользуясь соответствующими свойствами действий над векторами и известными векторными равенствами.
- Вернуться от векторного языка к геометрическому.
- Записать ответ.
Метод векторов чаще всего используется при решении задач, в которых требуется доказать: параллельность прямых (отрезков), деление отрезка в определенном соотношении; что три точки лежат на одной прямой; что данный четырехугольник — параллелограмм (ромб, прямоугольник, квадрат, трапеция). Проиллюстрируем суть этого метода на примере решения задачи.
Пример №8
Докажите, что середины сторон любого выпуклого четырехугольника являются вершинами параллелограмма.
Дано: 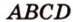
Доказать: 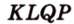
1. Переведем задачу на язык векторов, заменив отрезки векторами: 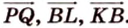
2. Воспользуемся правилом треугольника для сложения векторов: 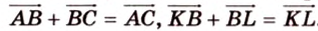
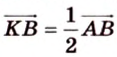
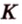
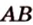
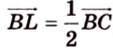
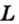
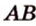
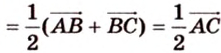
Поэтому 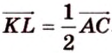
Аналогично 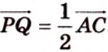
3. Поэтому 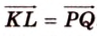
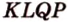
Почему именно так?
Переведя задачу на язык векторов, получаем требование задачи: доказать равность векторов 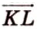
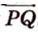
Однако 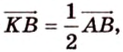
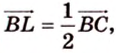
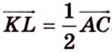
Аналогично получаем, что 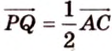
Таким образом, 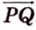
Метод координат
Решая задачу координатным методом, следует выполнить такие действия:
- Записать геометрическую задачу на языке координат.
- Преобразовать выражение или вычислить его значение.
- Перевести найденный результат на язык геометрии.
- Записать ответ.
Методом координат чаще всего решают задачи:
- на нахождение геометрических мест точек;
- на доказательство зависимостей между линейными элементами геометрических фигур.
Решая задачу методом координат, необходимо рационально выбрать систему координат: данную фигуру следует разместить относительно осей координат таким образом, чтобы как можно больше координат нужных точек равнялось нулю, а также одному и тому же числу. Например, координаты вершин прямоугольника 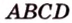
Проиллюстрируем суть метода координат на примере.
Пример №9
Докажите, что когда у параллелограмма диагонали равны, то он прямоугольник.
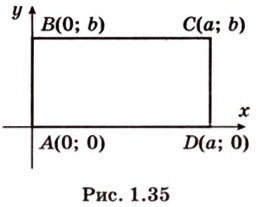
Разместим параллелограмм в системе координат таким образом, чтобы его вершины имели координаты: 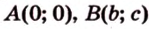
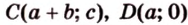
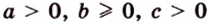
По условию 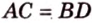
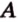
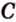
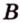
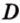
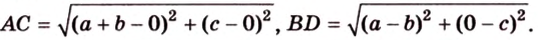
Тогда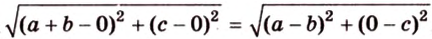
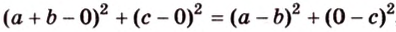
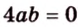
Поскольку 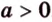
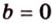
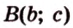
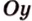
Поэтому угол 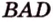
Метод геометрических преобразований: метод поворота, метод симметрии, метод параллельного переноса, метод гомотетии.
Решая задачи методом геометрических преобразований, наряду с данными фигурами рассматривают новые, полученные из данных с помощью определенного преобразования. Выясняют свойства новых фигур, переносят эти свойства на данные фигуры, а затем находят способ решения задачи.
Говорят, что задачи, решенные методами векторов, координат, геометрических преобразований, площадей и другими методами, в которых используется больше свойств геометрических фигур, решены геометрическими методами.
Геометрия — одна из древнейших математических наук. Первые геометрические факты отображены в вавилонских клинописных таблицах, египетских папирусах и других источниках VI-III в. до н.э.
Название науки «геометрия» происходит от двух древнегреческих слов: «geo» (гео) — земля и «metreo» (метрео) — измере ние. В развитии геометрии выделяют четыре основных периода.
Первый период — зарождение геометрии как науки — протекал в Древнем Египте, Вавилоне и Греции примерно до V в. до н.э. Именно тогда ученые установили первые общие закономерности в природе и воспроизвели их в зависимостях между геометрическими величинами. Основной проблемой геометров того периода было вычисление некоторых площадей и объемов. Логических обоснований в задачах было очень мало. В основном геометрические свойства доказывались практическими наблюдениями, поиском закономерностей, экспериментальным путем, т.е. эмпирически.
Второй период — формирование геометрии в структурную систему. В VII в. до н.э. центром развития геометрии стала Греция. Древние геометры работали над систематизацией накопленных и новых знаний, устанавливали связи между геометрическими фактами, разрабатывали приемы доказательств. Значительный вклад в развитие математики, в частности геометрии, в этот период сделали Пифагор, Платон, Аристотель, Фалес, Анаксигор, Демокрит, Евклид. В книге «Начала» Евклида сформулированы понятия о фигуре, о геометрическом утверждении и доказательстве. Они остаются актуальными и сегодня.
Третий период — дополнение геометрии новыми методами -начался в первой половине XVII в., когда французский ученый Рене Декарт разработал метод координат, связавший евклидову геометрию с алгеброй и математическим анализом. Использование методов этих наук в геометрии дало возможность создать новые науки — аналитическую, а позднее — дифференциальную геометрию, проективную и начертательную геометрию. Таким образом, евклидова геометрия поднялась на качественно новую ступень по сравнению с геометрией древних: в ней рассматривались гораздо более общие фигуры и использовались новые методы.
Четвертый период — создание неевклидовой геометрии -связан с именем российского ученого Николая Ивановича Лобачевского, открывшего в 1826 г. возможности для создания неевклидовых геометрий. Им была построена совершенно новая, неевклидова геометрия, которую теперь называют геометрией Лобачевского.
Особенность начатого Н.И. Лобачевским периода в истории геометрии состоит в том, что после его открытия начали развиваться новые геометрические теории, новые «геометрии» и соответствующие обобщения самого предмета геометрии. В этот период возникло понятие о разновидностях пространства (термин «пространство» в науке может означать как обычное реальное пространство, так и абстрактное, «математическое», пространство). Некоторые теории создавались внутри евклидовой геометрии, как ее особые разделы, а позднее приобретали статус самостоятельных. Другие, подобно геометрии Лобачевского, вводили изменения аксиом и структурировались на основе этих изменений, обобщая и строя науку.
Именно так была создана геометрия Римана (Георг Фридрих Бернхард Риман (1826-1866) — немецкий ученый) и ее обобщения (1854-1866), получившие применение в теории относительности, механике и др.
В школьном курсе мы изучаем геометрию Евклида. Перевел труд древнегреческого ученого «Начала» украинский математик Михаил Егорович Ващенко-Захарченко (1825-1912) в 1880 г. На основе этой книги написано множество учебников по геометрии. Например, преподавание геометрии в советской школе почти до 1982 г. осуществлялось по учебнику российского педагога-математика А.П. Киселева (1852-1940). В 1980-х годах украинским математиком А.В. Погореловым было создано новое учебное пособие. Его и сегодня можно найти в библиотеках общеобразовательных учебных заведений.
Современная геометрия является многовекторной и стремительно развивается в совокупностях математических теорий, изучающих различные пространства и их фигуры. Значительный вклад в геометрию сделали и наши соотечественники: М.В. Остроградский, А.М. Астряб, А.П. Киселев, А.Д. Александров, А.Н. Колмогоров, А.В. Погорелов и др.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Стереометрия — формулы, определение и вычисление
- Возникновение геометрии
- Призма в геометрии
- Цилиндр в геометрии
- Ортогональное проецирование
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:22. Взаимное расположение прямой и плоскости в пространствеСкачать

Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности
Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности.
Прямые, отрезки и углы, связанные с окружностью:

Взаимное расположение окружности и прямой:
1. Окружность и прямая не имеют общих точек
2. Окружность и прямая имеют 2 общие точки (l — секущая)
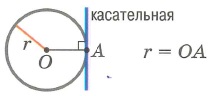
3. Окружность и прямая имеют 1 общую точку (l — касательная)
Взаимное расположение окружности и точки:
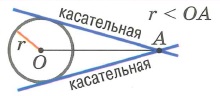
1. Точка лежит вне окружности (2 касательные через точку А)
2. Точка лежит внутри окружности (нет касательных через точку А)
3. Точка лежит на окружности (1 касательная через точку А)
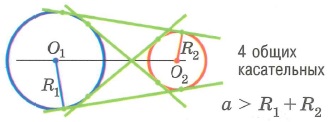
Взаимное расположение двух окружностей:
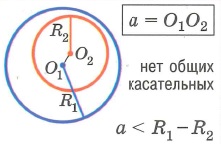
1. Одна окружность лежит внутри другой.
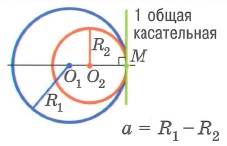
2. Одна окружность касается другой изнутри.
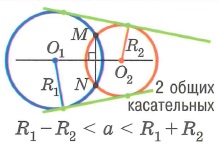
3. Окружности пересекаются.
4. Одна окружность касается другой снаружи или одна окружность лежит вне другой.
Свойства углов, связанных с окружностью:
Вписанный угол равен половине центрального, опирающегося на ту же дугу:

Любые два вписанных угла, опирающиеся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°=π
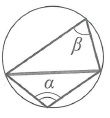
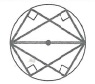
Угол между пересекающимися хордами:
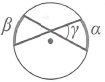
Угол между секущими, пересекающимися вне окружности:
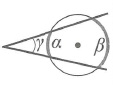
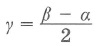
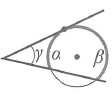
Угол между касательными:
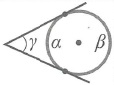
Угол между касательной и хордой:

Метрические соотношения в окружности (длины отрезков):
Отрезки пересекающихся хорд связаны соотношением:
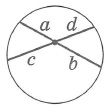
Отрезки касательных, проведенных из общей точки, равны:
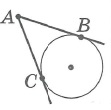
Квадрат длины отрезка касательной равен произведению длин отрезков секущей, проведенной из той же точки:
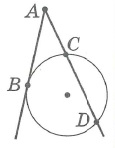
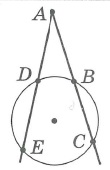
Произведения длин отрезков секущих, проведенных из общей точки, равны:
Консультации и техническая
поддержка сайта: Zavarka Team
📸 Видео
10 класс, 11 урок, Числовая окружностьСкачать

Окружность и прямая: варианты взаимного расположенияСкачать

Взаимное расположение окружностей. Практическая часть. 7 класс.Скачать

Длина окружности. Площадь круга. 6 класс.Скачать


































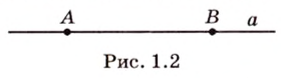

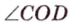 и
и 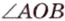 ,
, 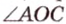 и
и 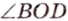 — вертикальные;
— вертикальные;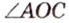 и
и 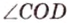 ,
, 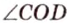 и
и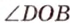 ,
, 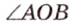 и
и 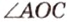 ,
, 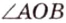 и
и 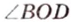 — смежные.
— смежные.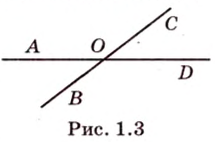
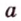 и
и 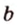 третьей прямой внутренние (или внешние) разносторонние углы равны или внутренние односторонние в сумме составляют 180°, то
третьей прямой внутренние (или внешние) разносторонние углы равны или внутренние односторонние в сумме составляют 180°, то 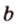 параллельны.
параллельны.

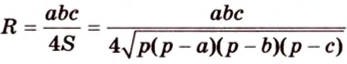
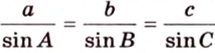 ;
;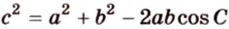 (квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними).
(квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними).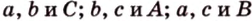 ;
;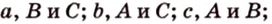
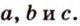
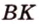 — медиана,
— медиана, 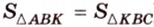 ).
).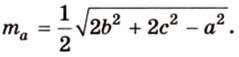
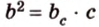 и
и 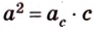 (рис. 1.19).
(рис. 1.19).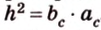 .
.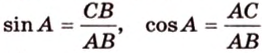

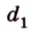 и
и 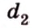 ) равна сумме квадратов всех его сторон:
) равна сумме квадратов всех его сторон: